ESERCITAZIONE V_CALCOLO SU EXCEL DEL CENTRO DELLE RIGIDEZZE DI UN TELAIO SHEAR-TYPE E VERIFICA SU SAP_TRIGGIANI Federica

CALCOLO DEL CENTRO DI RIGIDEZZA IN UN IMPALCATO CON TELAIO SHEAR-TYPE

Analisi del comportamento di un impalcato sollecitato da forze esterne orizzontali e del comportamento dei controventi nel rispondere a tali sollecitazioni.
I controventi vengono rappresentati come delle molle, in quanto rappresentano dei vincoli elastici, cioè in grado di rispondere alle forze esterne subendo una deformazione reversibile.
La capacità di queste molle di rispondere alle forze esterne sarà strettamente collegata alla loro rigidezza k e alla loro distanza dal CENTRO DELLE RIGIDEZZE, unico punto in cui la risultante delle forze esterne applicate avrà momento pari a zero e dunque rotazione nulla.
Dunque una volta determinate le caratteristiche dimensionali e tipologiche dell’ impalcato e il materiale dei suoi elementi, attraverso un file excel si calcolerà il CENTRO DELLE RIGIDEZZE.

Scelgo di analizzare il seguente impalcato in calcestruzzo: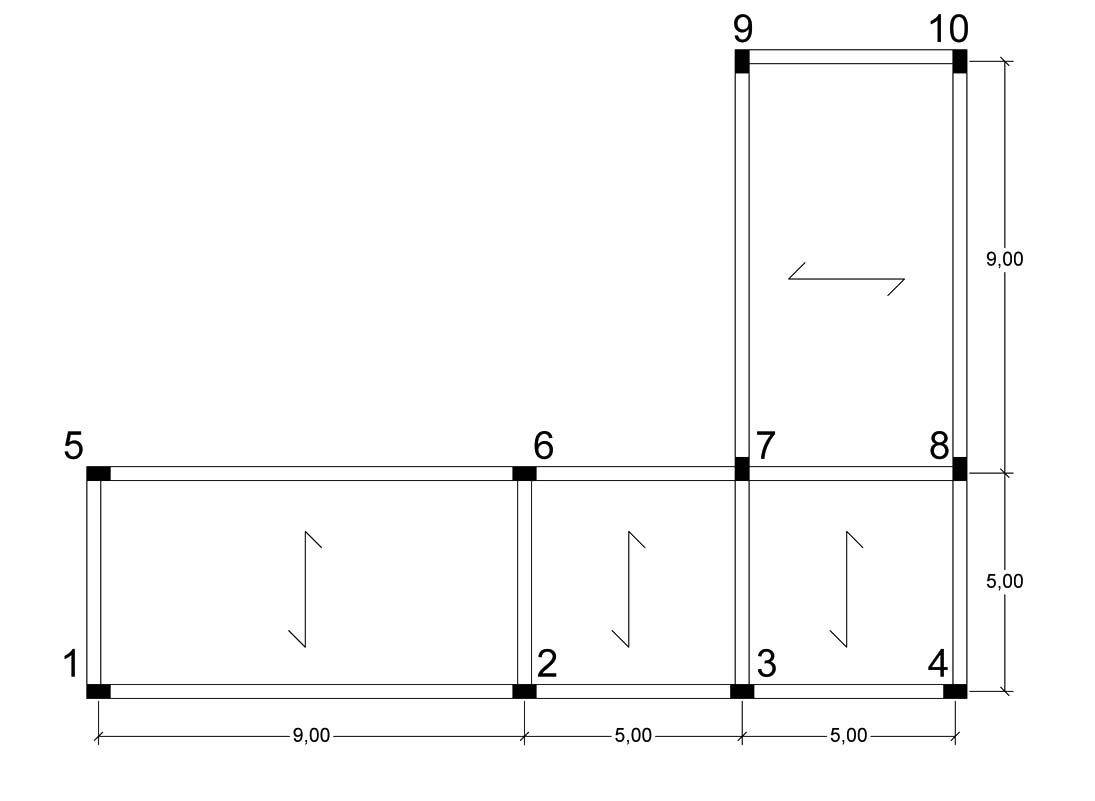

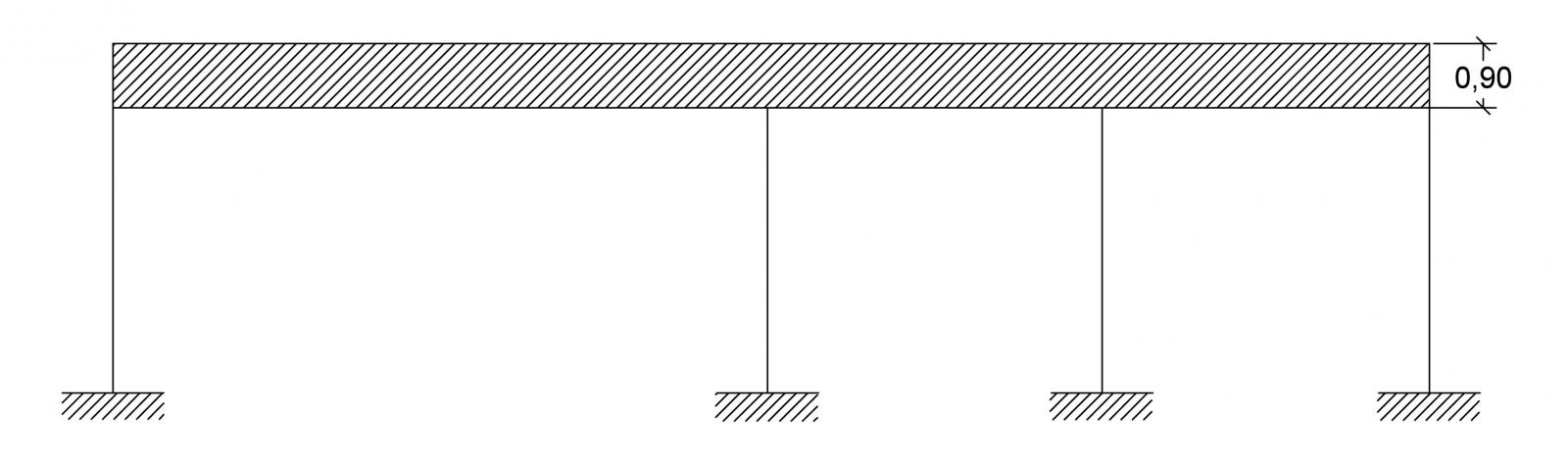
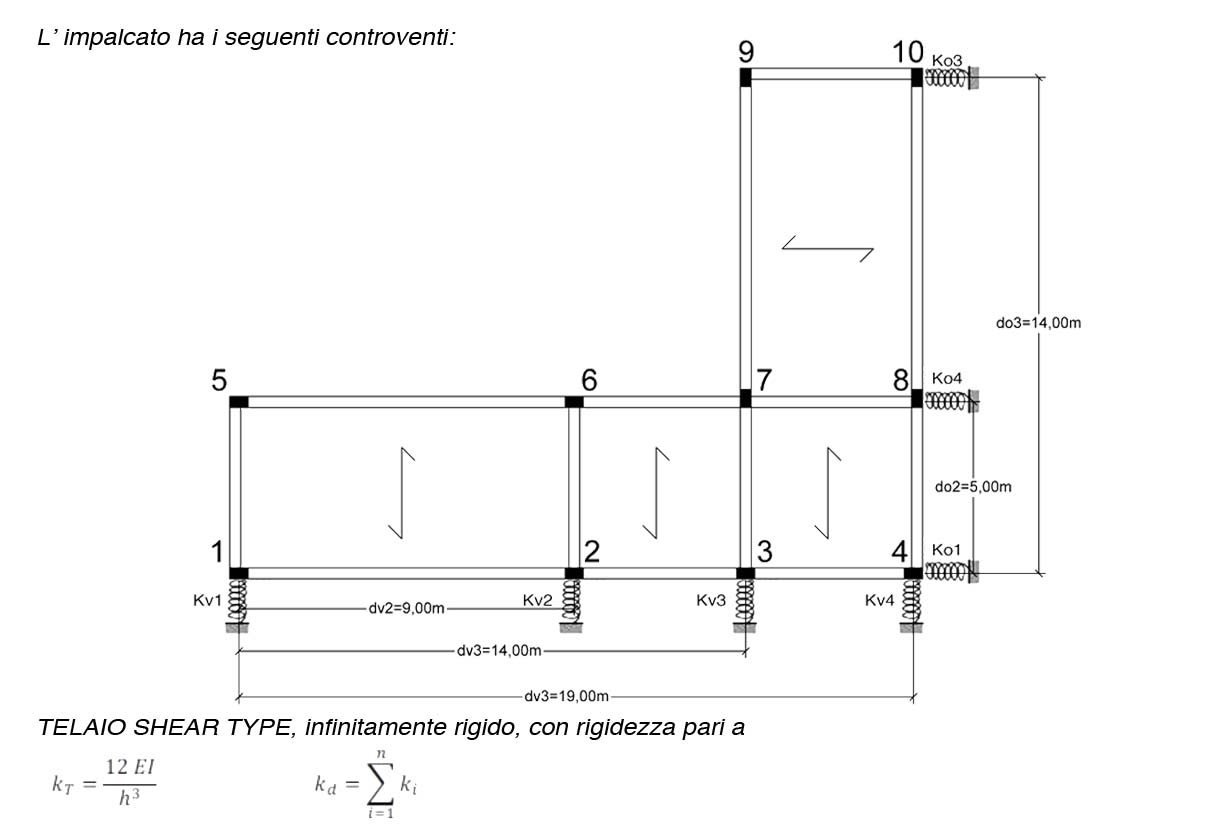
H PILASTRI: 4,00 m
PILASTRI IN CEMENTO ARMATO __ MODULO DI YOUNG : E= 21000 Nmm
SEZIONE PILASTRI:  30 x 50 cm

A seconda dell’ orditura del telaio avremo i pilastri orientati in 2 diversi modi e di conseguenza con diversi MOMENTI DI INERZIA.

Prima di procedere con i calcoli su excel definisco la suddivisione dei telai con le rispettive numerazioni dei pilastri di un determinato pilastro, a seconda che io stia analizzando l’impalcato rispetto ai controventamenti lungo l’asse x e poi lungo l’asse y.
TELAIO VERTICALE____ LUNGO Y-Z                                 TELAIO ORIZZONTALE____LUNGO X-Z       
                                   
TELAIO 1 _ PILASTRI 1-5                                                  TELAIO 5 _ PILASTRI 1-2-3-4
TELAIO 2 _ PILASTRI 2-6                                                  TELAIO 6 _ PILASTRI 5-6-7-8
TELAIO 3 _ PILASTRI 9-7-3                                              TELAIO 7 _ PILASTRI 9-10
TELAIO 4 _ PILASTRI 10-8-4          

STEP 1 Calcolo delle RIGIDEZZE TRASLANTI dei controventi dell’edificio.
La rigidezza traslante dei controventi presi in analisi è dato dalla somma delle rigidezze di ciascun pilastro.
                                        

STEP 2     Tabella sinottica dei controventi e delle loro distanze dell’origine
Ci permette di raccogliere dati sulle rigidezze traslanti prima ottenute e sulle loro distanze rispetto al centro 0, le quali dipendono dagli interassi e dalle luci tra i pilastri. 

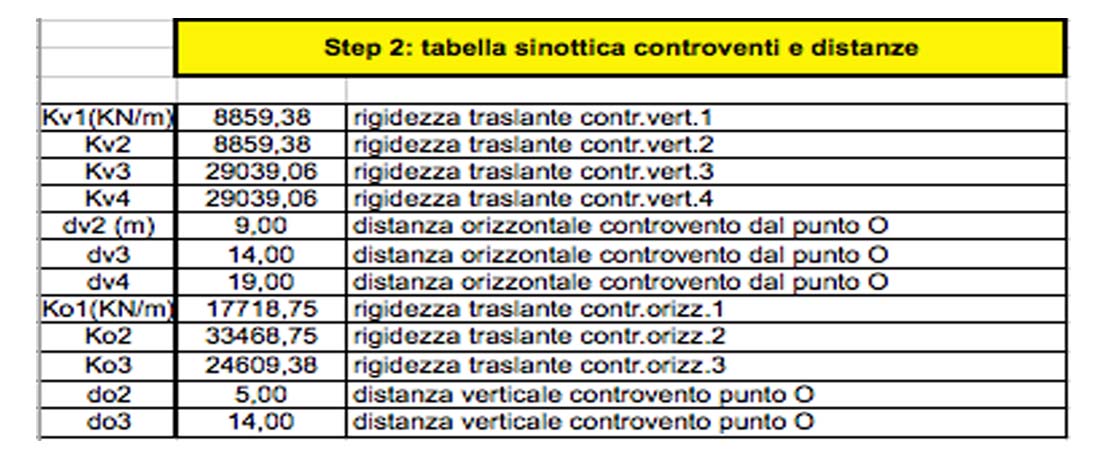
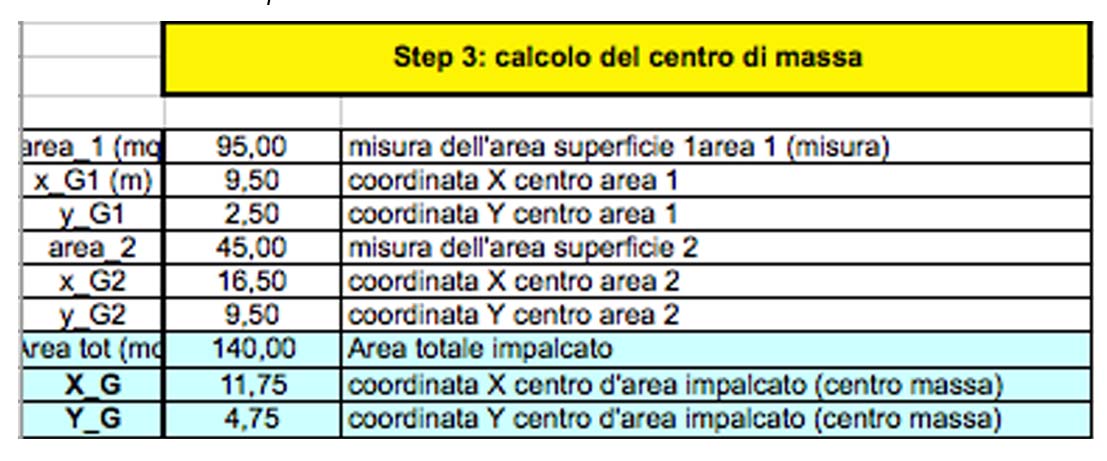
STEP 3      Calcolo del CENTRO DELLE MASSE

Conviene suddividere la pianta dell’ impalcato in aree geometriche regolari per determinarne facilmente il BARICENTRO.

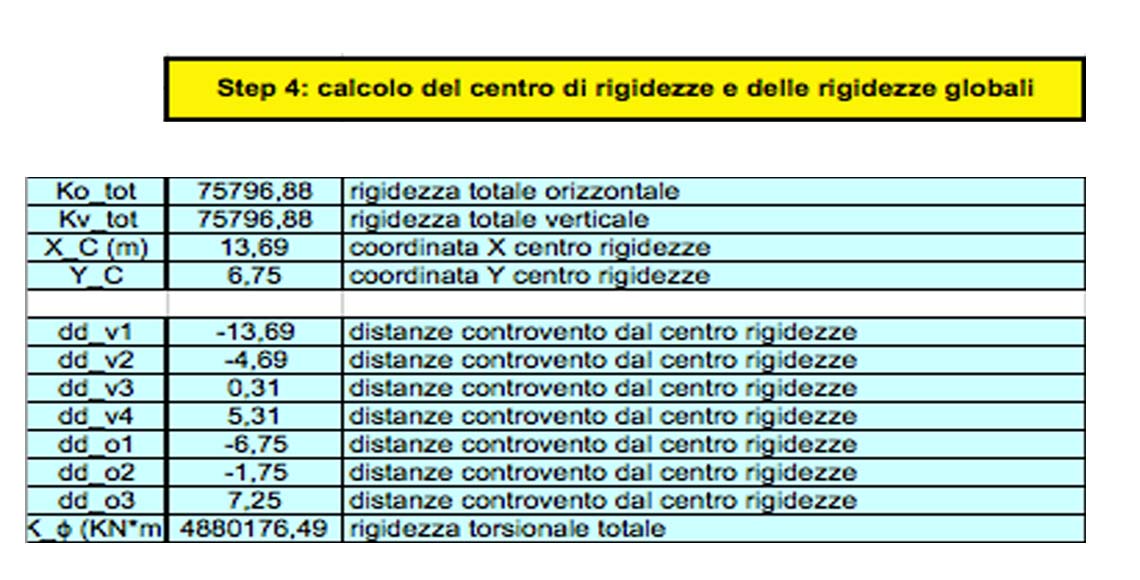
STEP 4  Calcolo del CENTRO DELLE RIGIDEZZE e delle RIGIDEZZE GLOBALI:
Sommo le rigidezze verticali e poi le rigidezze orizzontali;
Trovo la rigidezza totale orizzontale e verticale e faccio una media ponderata tra le due;
Per il CENTRO DELLE RIGIDEZZE calcolo, per ogni molla, la sua rigidezza per il suo braccio (distanza dal punto considerato come origine);
Sommo tutti i prodotti ottenuti nelle due direzioni e li divido per la rigidezza globale
Noto il centro delle rigidezze C calcolo la distanza di ogni telaio da esso. 
Calcolo la RIGIDEZZA ROTAZIONALE K che è data dalla somma dei prodotti de
Ora che il centro delle rigidezze è noto possiamo calcolare la distanza di ogni telaio da C; non rimane ora che calcolare la RIGIDEZZA ROTAZIONALE K che è data dalla sommatoria dei prodotti delle rigidezze traslanti di ciascun telaio per la distanza al quadrato di ognuno di essi rispetto a C.

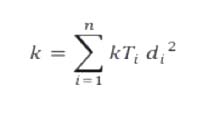
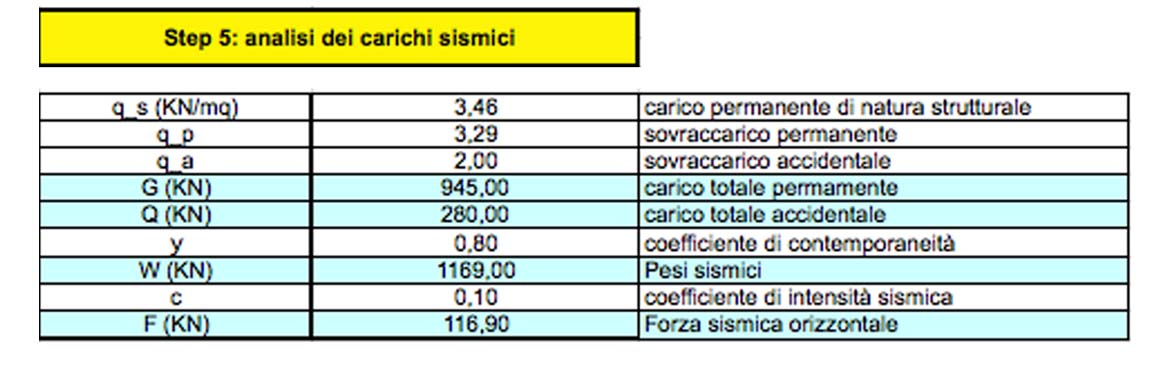
STEP 5 Analisi dei carichi sismici:
Successivamente, dopo aver individuato il carico q del solaio (ricordando che q =qp + qs + qa), lo moltiplico per il coefficiente di contemporaneità per ottenere i pesi sismici. Tali pesi vengono moltiplicati per il coefficiente di intensità sismica, per ricavarne il valore dell’ipotetica forza sismica agente (premettendo che tale valore è comunque imprevedibile. Infatti il coefficiente di intensità sismica ha un valore molto elevato).

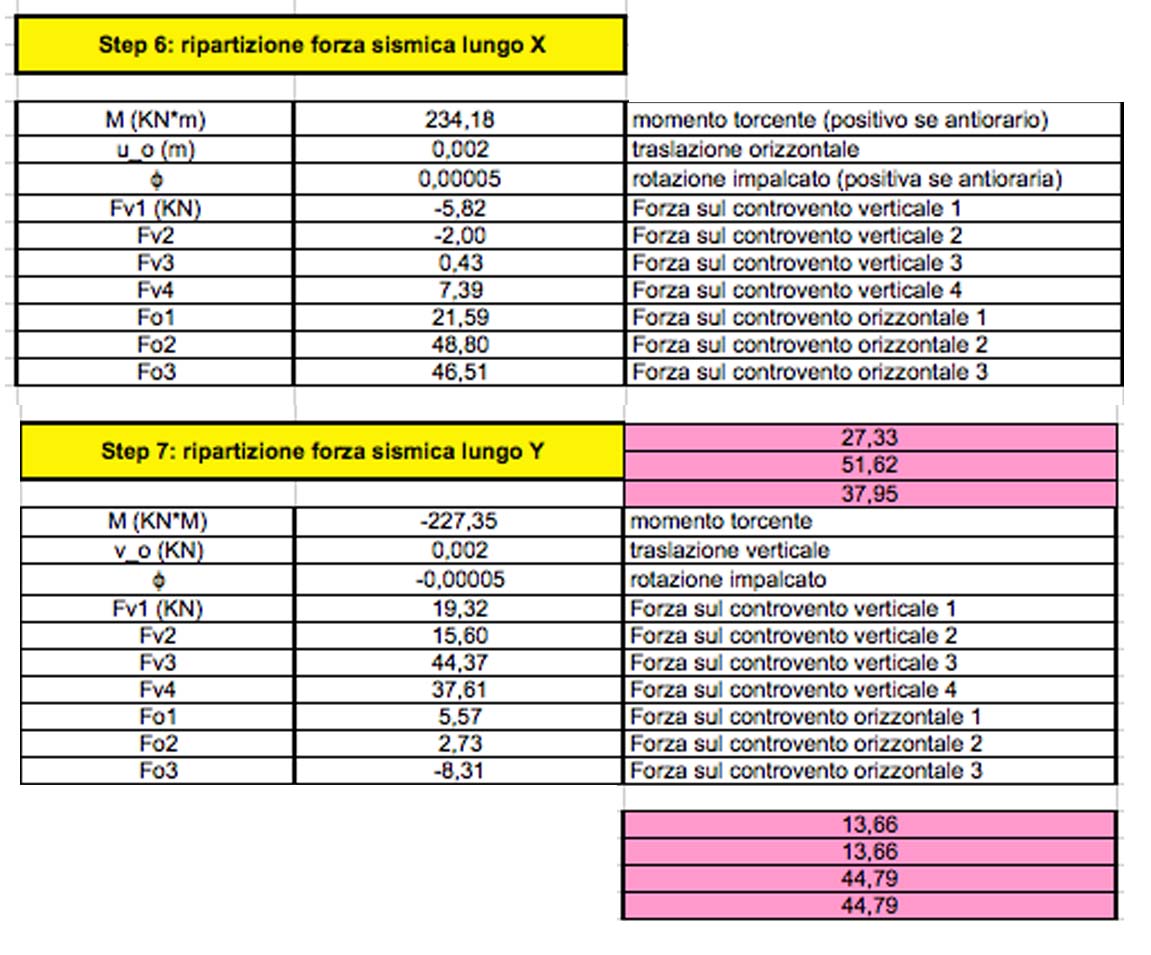
STEP 6 e 7: Ripartizione della forza sismica lungo X e Y:

Individuo come l’ipotetica forza sismica si ripartisce nelle due direzioni. Nel mio caso il centro delle rigidezze e il centro delle masse NON coincidono, pertanto avrò una rotazione data dalla forza moltiblicata per il braccio, il cui valore coincide con la differenza tra il centro delle masse e il centro delle rigidezze, rispettivamente all’ asse x e all’ asse y.

Il foglio di calcolo trova automaticamente la traslazione orizzontale Ux e la traslazione verticale Uy, la rotazione dell’ impalcato. Con questi dati è possibile calcolare ulteriormente come si ripartisce la forza sismica su ciascuna molla. 
Moltiplico la rigidezza della molla per la somma tra lo spostamento (ad essa perpendicolare) ed il prodotto tra rotazione e distanza dal centro delle rigidezze. 
Ricavo infine le reazioni con cui ciascuna molla reagisce e contrasta la forza orizzontale sismica in ordine di numerazione da ko1 a ko3 su x, da kv1 a kv4 su y.

Ora su SAP rifaccio la struttura sopra analizzata e imposto la forza del sisma sul centro delle rigidezze calcolato precedentemente. Verifico così la corrispondenza dei valori e soprattutto che la deformazione subita dall'impalcato sia la sola traslazione ma non la rotazione.

Importiamo la struttura da Rhino su SAP

Selezioniamo tutti i nodi a terra di tutti i pilastri e assegnamo gli incastri a terra.  (Assign -> Joint -> Restraints)

A questo punto selezioniamo prima i pilastri e poi le travi e ne definiamo la sezione e il materiale (calcestruzzo).

Per quanto riguarda i pilastri dobbiamo fare attenzione a selezionare quelli disposti in orizzontale e assegnarli una sezione di 30x50, e a quelli in verticale una sezione 50x30.

(Assign -> Frame -> Frame Section -> dal menù a tendina seleziono  “CONCRETE")

Per aumentare la rigidezza delle travi ed assimilarle al modello di telaio SHEAR-TYPE, infinitamente rigido:

Assign -> Frame -> Property Modifiers -> Aumento il Momento d' Inerzia

A questo punto imposto il CENTRO DELLE RIGIDEZZE secondo le coordinate calcolate dal foglio di calcolo (X=13,69 ; Y=6,75).

Successivamente applichiamo la forza sismica orizzontale nel centro delle rigidezze.             

Prima di procedere con l'analisi imposto seleziono tutti i nodi, compreso il punto in cui è impostata l'azione sismica, e assegno il Diaphragm Constraint.

A questo punto avvio l' analisi. 

Vediamo i diagrammi e i valori del Momento 33.