Esercitazione 4_Calcolo del centro delle rigidezze e ripartizioni delle forze sismiche

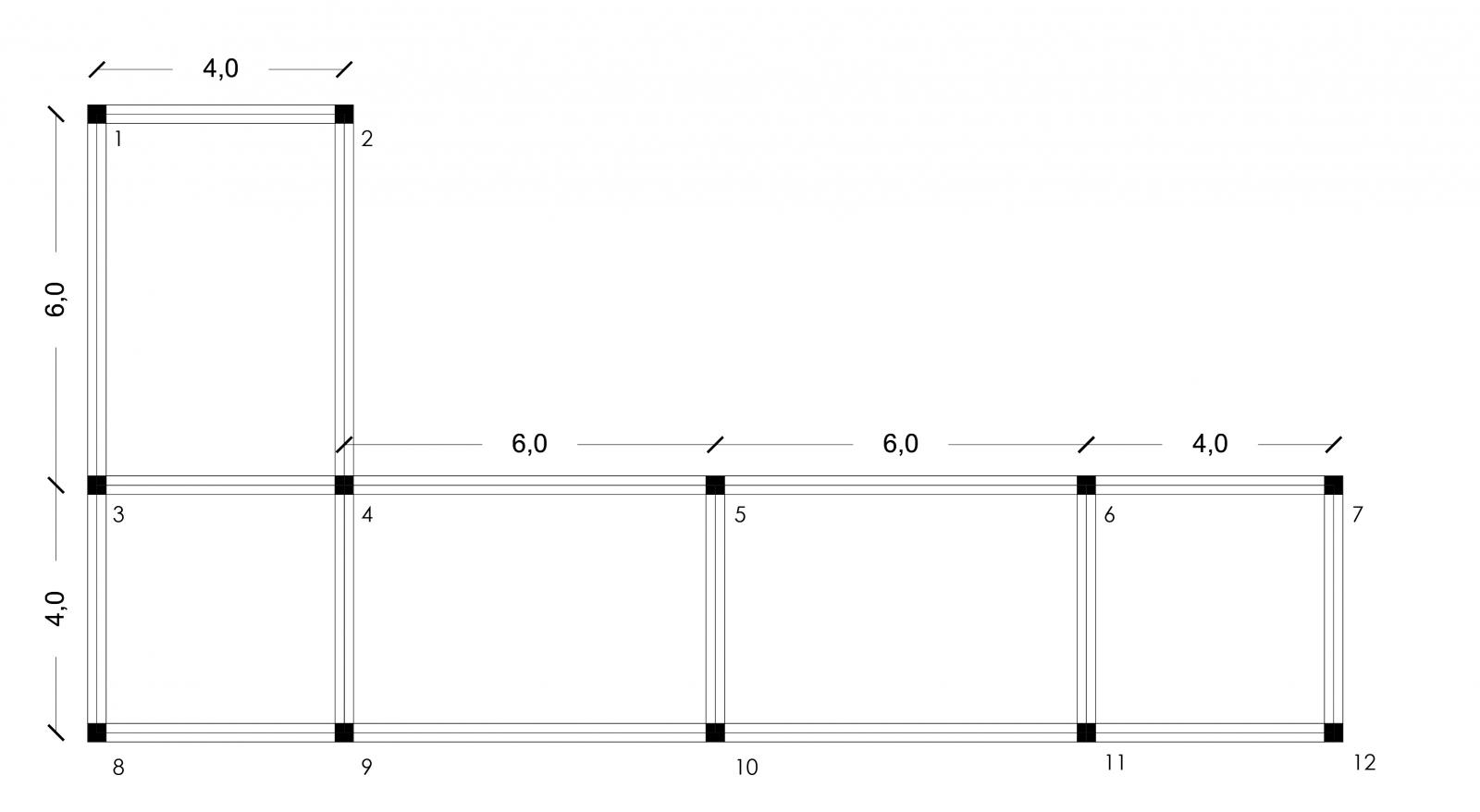
Andiamo a calcolare il centro delle rigidezze di un impalcato in cemento armato avente 5 telai verticali e 3 orizzontali.
Tale tipo di studio ci porterà a capire meglio il funzionamento di telai non solo sottoposti ad azioni verticali.  Infatti, un telaio, se ben pensato in fase progettuale, può resistere anche alle azioni orizzontali a cui la struttura è sottoposta, quindi agire da vero e proprio controvento.

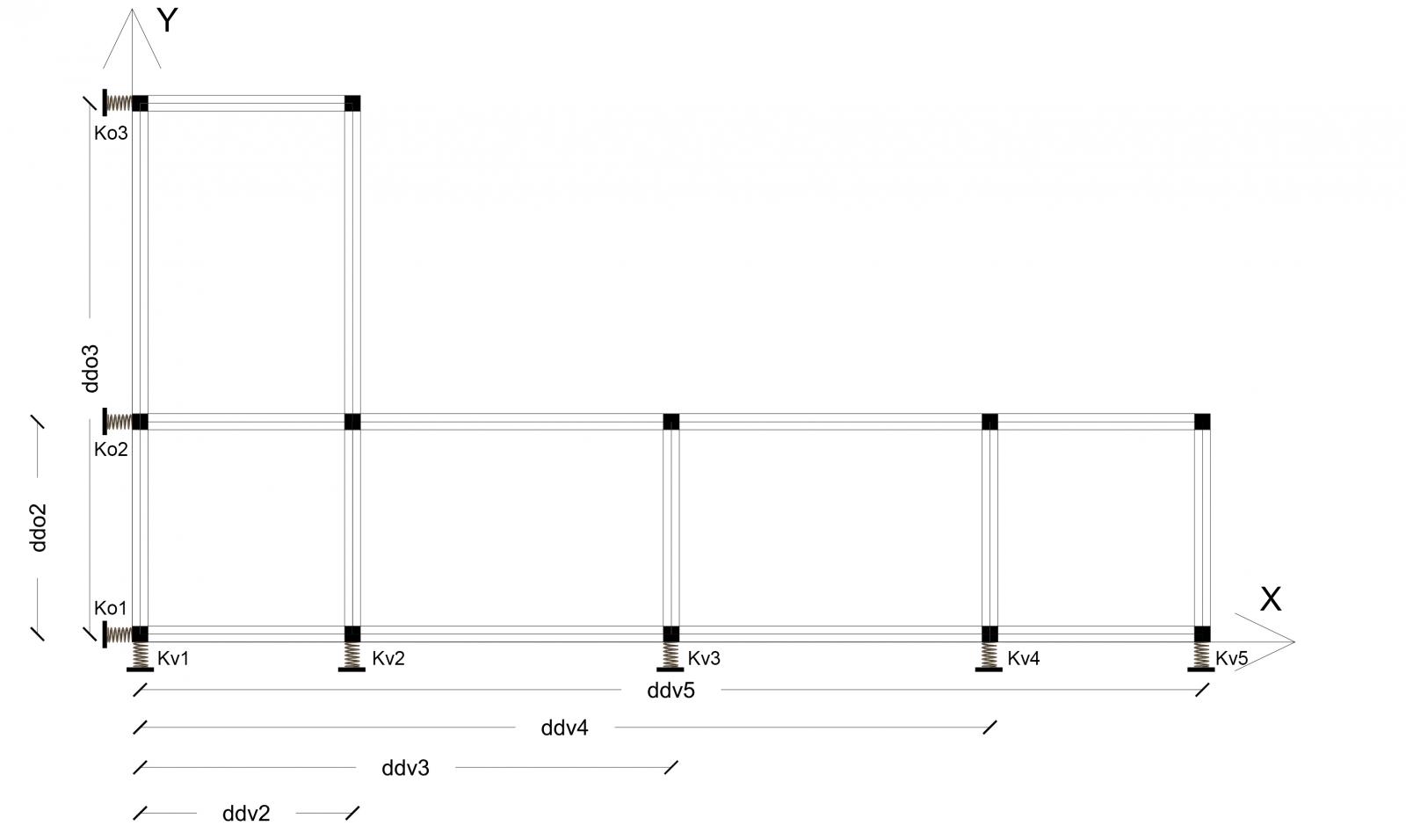
Disegniamo ora le rigidezze (Kv e Ko) dei singoli telai. Per essere rappresentate useremo un avatar, una molla, che meglio raffigura la reazione alle spinte orizzontali di questi controventi.
Aggiungiamo anche gli assi X e Y, dato che ci servirà un punto di origine su cui fare calcoli di natura geometrica.

Procediamo ora su Excel.
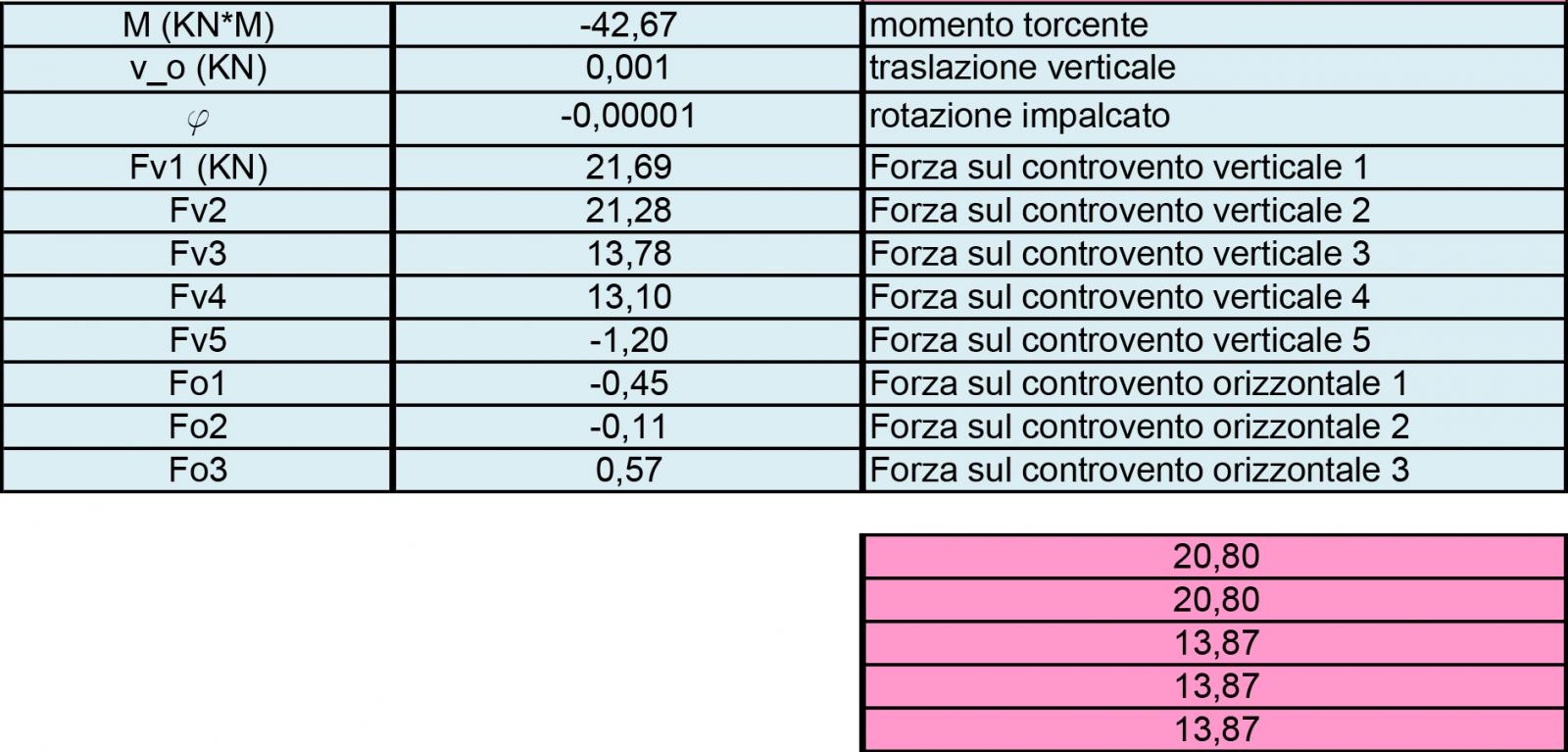
Tramite questo algoritmo è possibile calcolare centro di massa, centro delle rigidezze e ripartizioni delle forze sismiche.
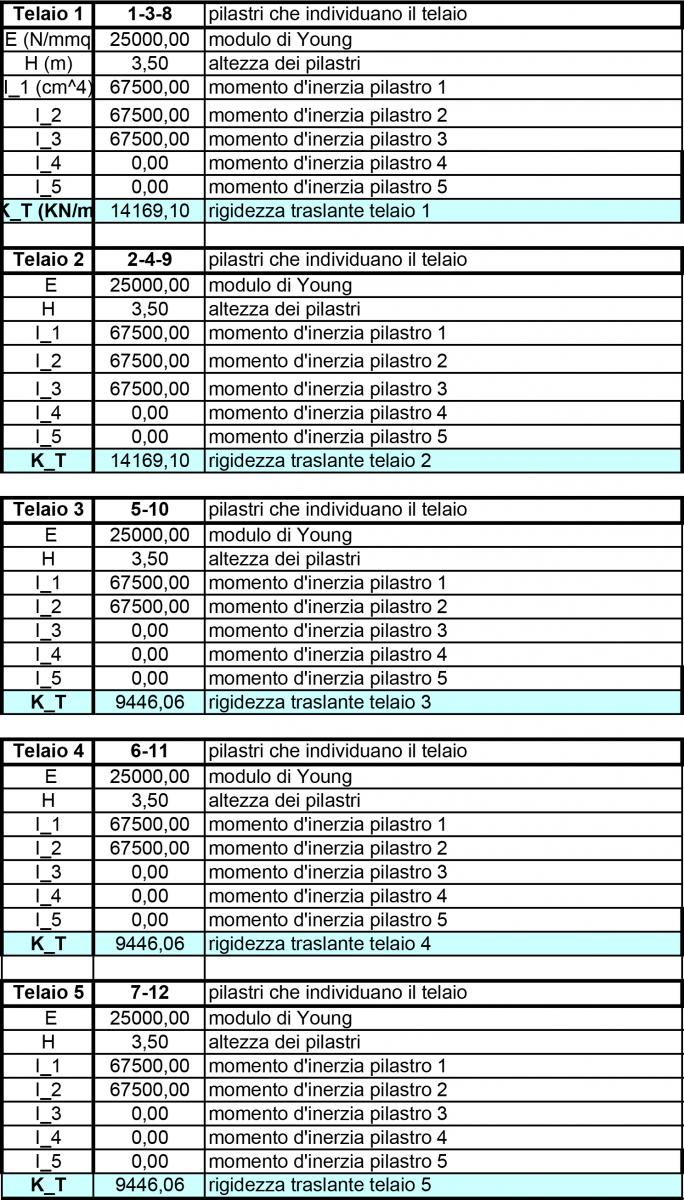
Primo passo, calcolare la rigidezza di ogni singolo controvento. Per fare ciò, necessitiamo modulo di Young (a seconda del materiale), momento di inerzia (che ovviamente varierà in caso vari la sezione) di ogni pilastro, e altezza.
Per il momento di inerzia, data la forma quadrata del pilastro, useremo la formula b^4/12 (b*h^3/12 con h e b uguali).
Dato che il nostro telaio è di tipo Shear-Type la struttura orizzontale è infinitamente rigida e quindi indeformabile assialmente mentre i pilastri sono soggetti a flessione. La trave perciò si muoverà con atto di moto rigido. Dato l’incastro dei pilastri a terra quindi, gli unici spostamenti saranno nella testa del pilastro, e uguali per tutti i pilastri che compongono il singolo telaio. La rigidezza traslante (K) quindi sarà calcolata come:
K=12*E*Itot/h^3

Telai verticali:

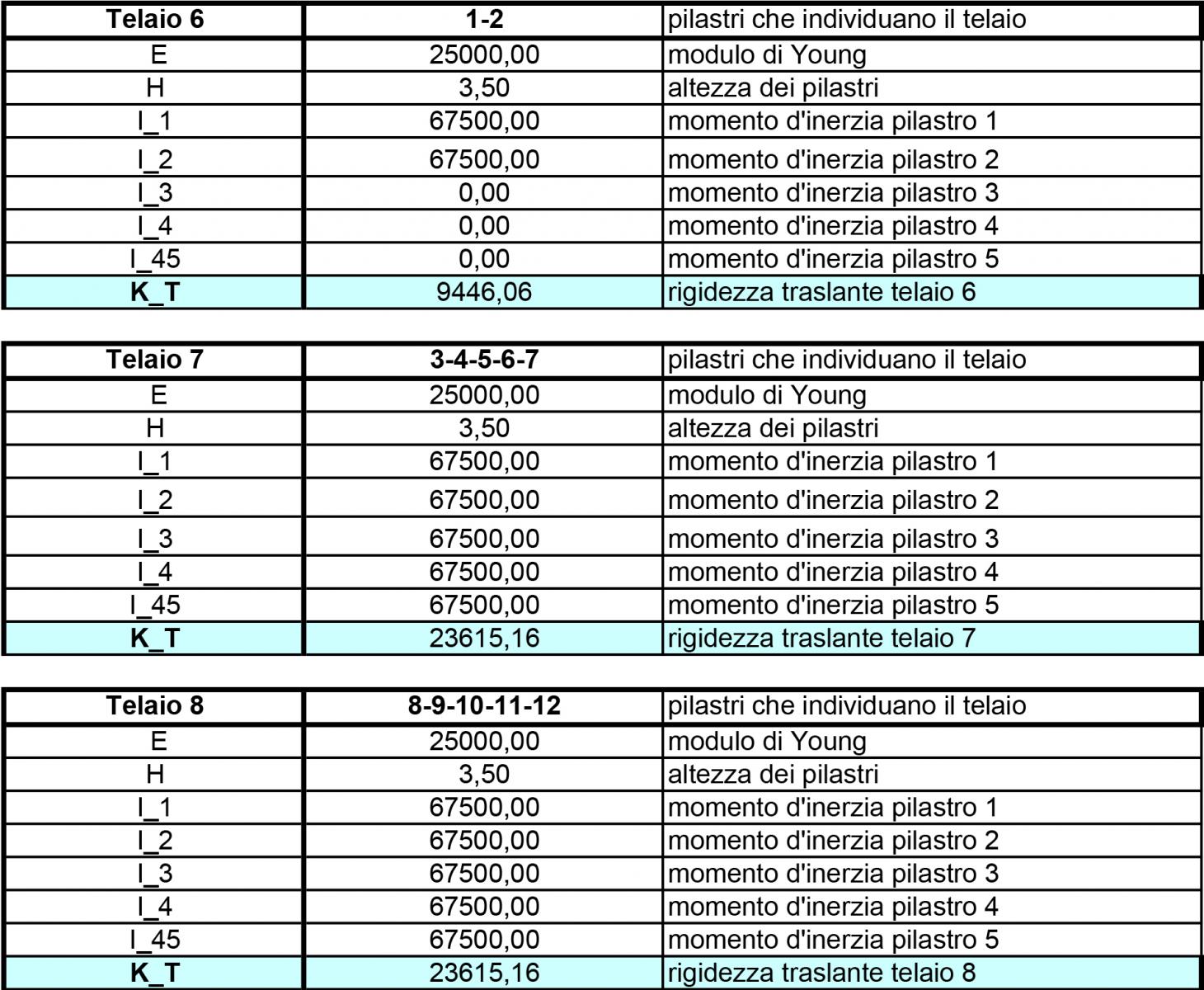
Telai orizzontali:

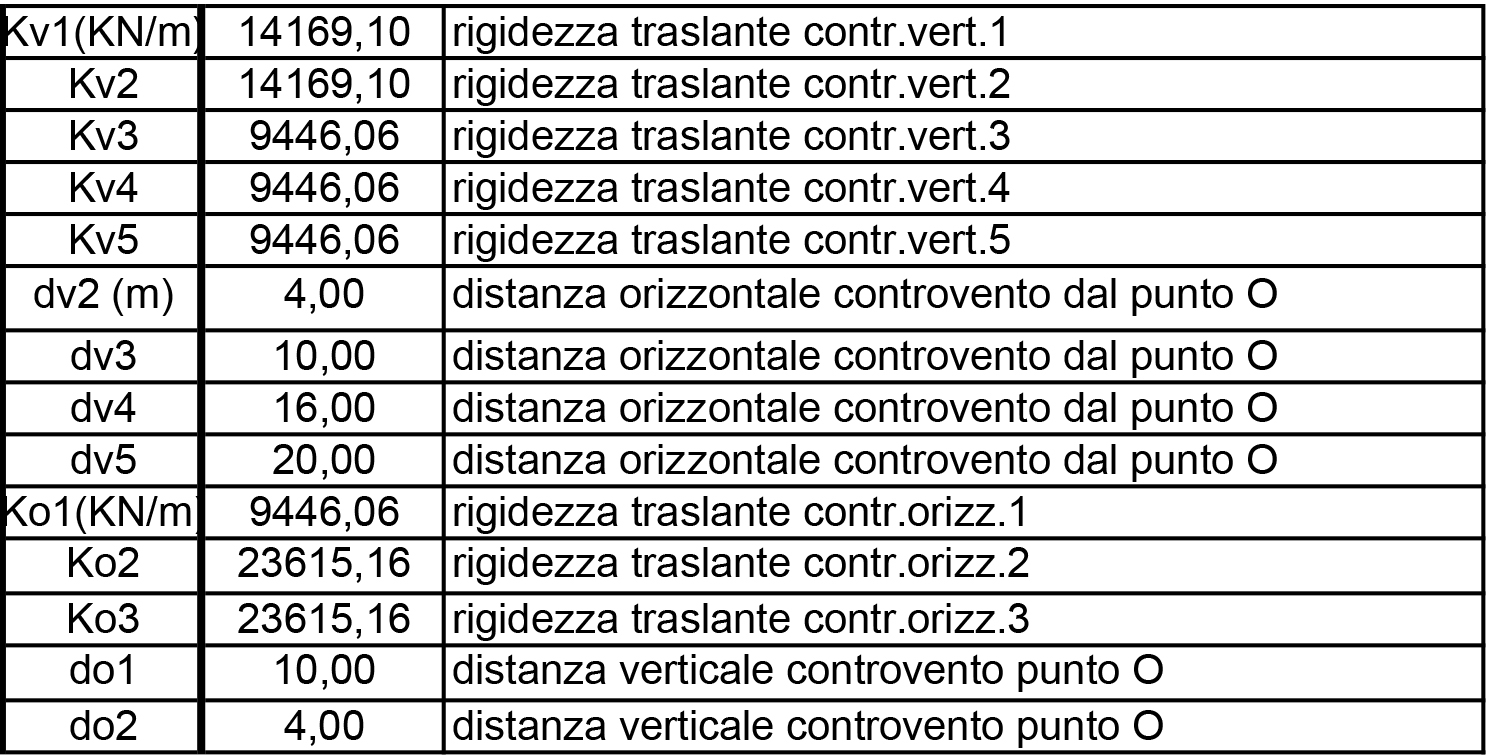
Elenchiamo ora le distanze orizzontali e verticali dei singoli controventi rispetto all’origine:

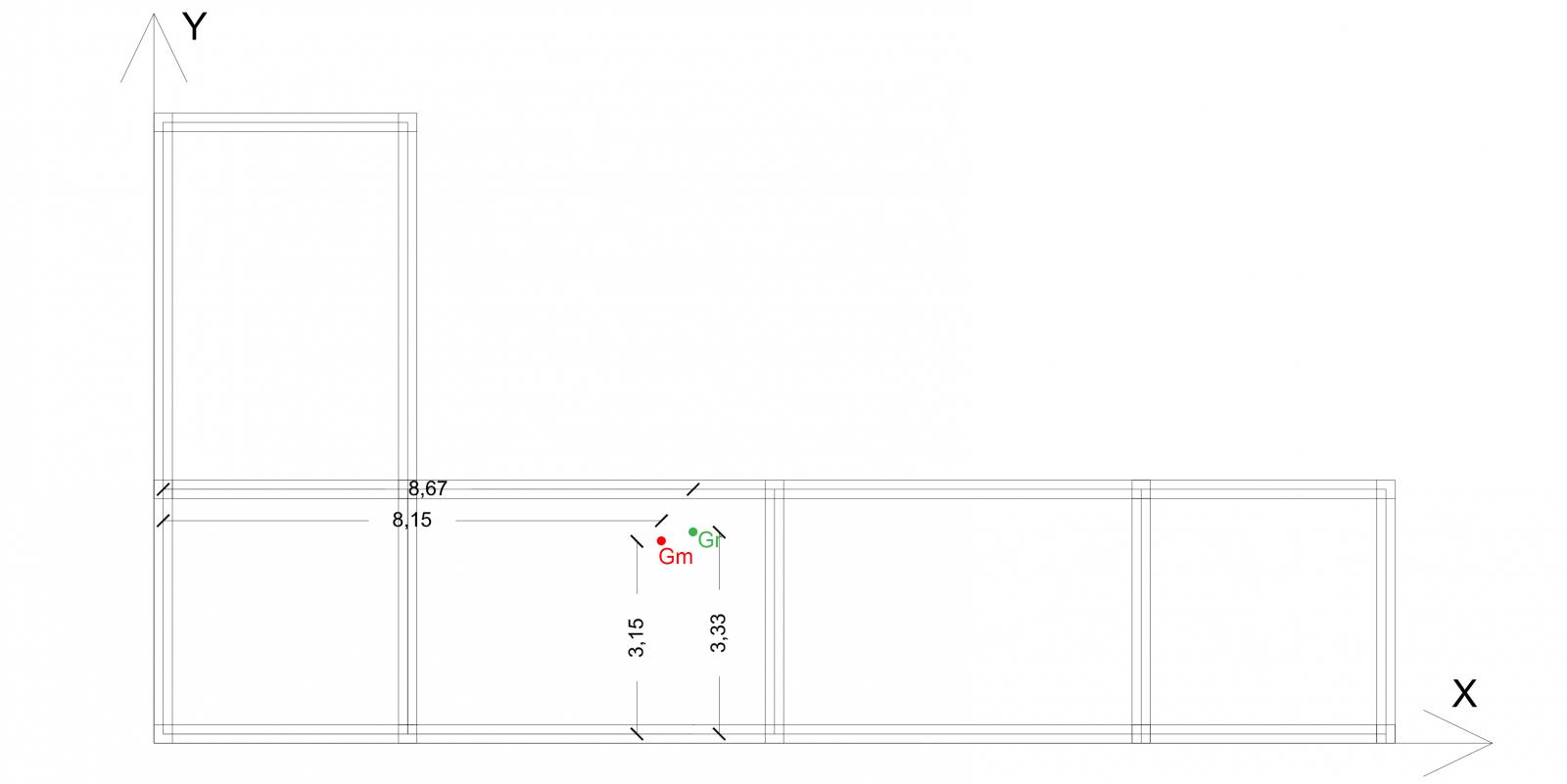
Suddividiamo ora l’impalcato in figure geometriche semplici di cui possiamo trovare i centri di massa:

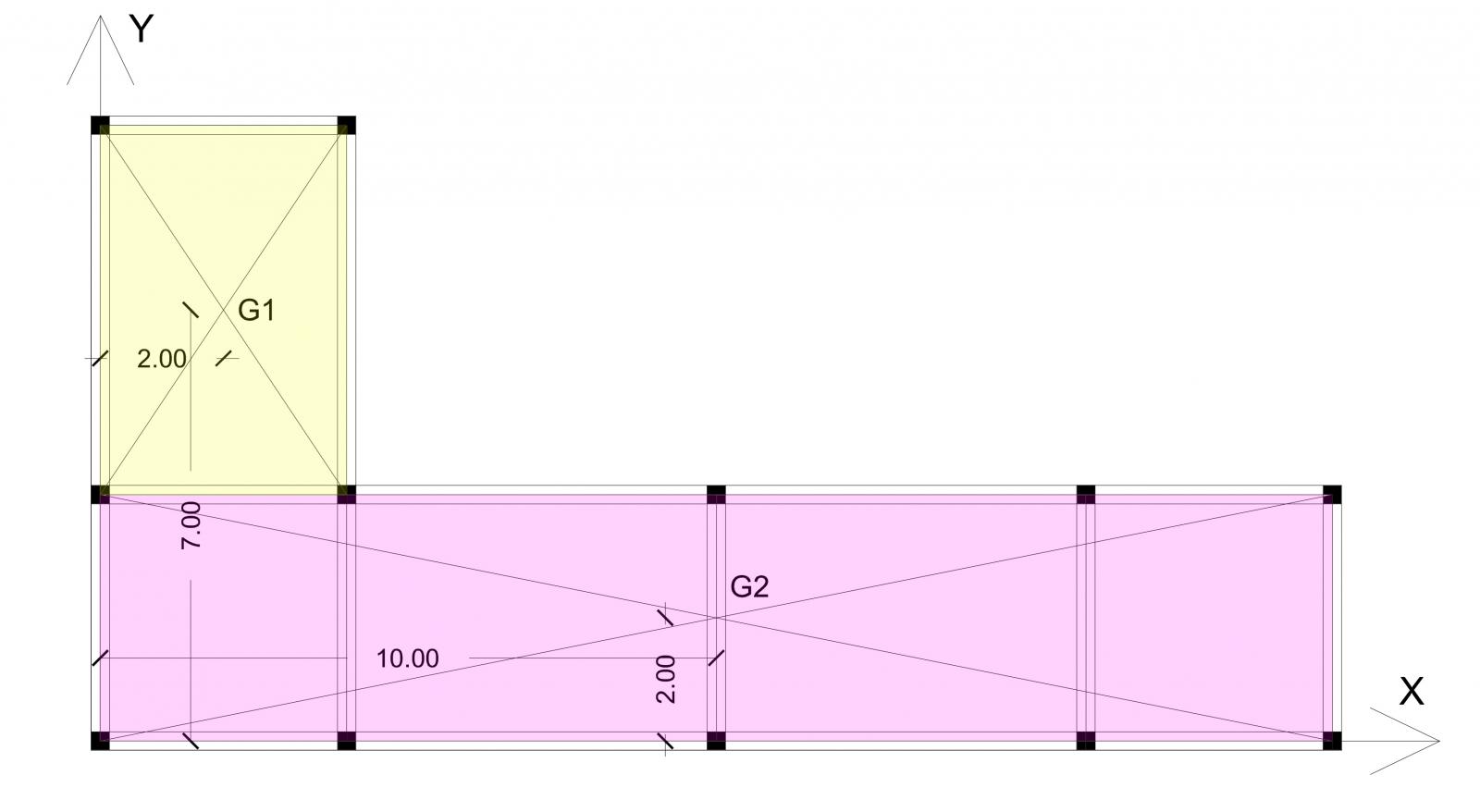
Possiamo ora trovare il centro di massa dell’intera struttura. Le coordinate di tale centro possono essere trovate come sommatoria delle distanze dei singoli centri di massa rispetto agli assi (y o x a seconda di ciò che si vuole calcolare) moltiplicate per le rispettive aree e dividendo il totale per l’area complessiva.
Gmx=∑xG*Ai/Atot
Gmy=∑yG*Ai/Atot

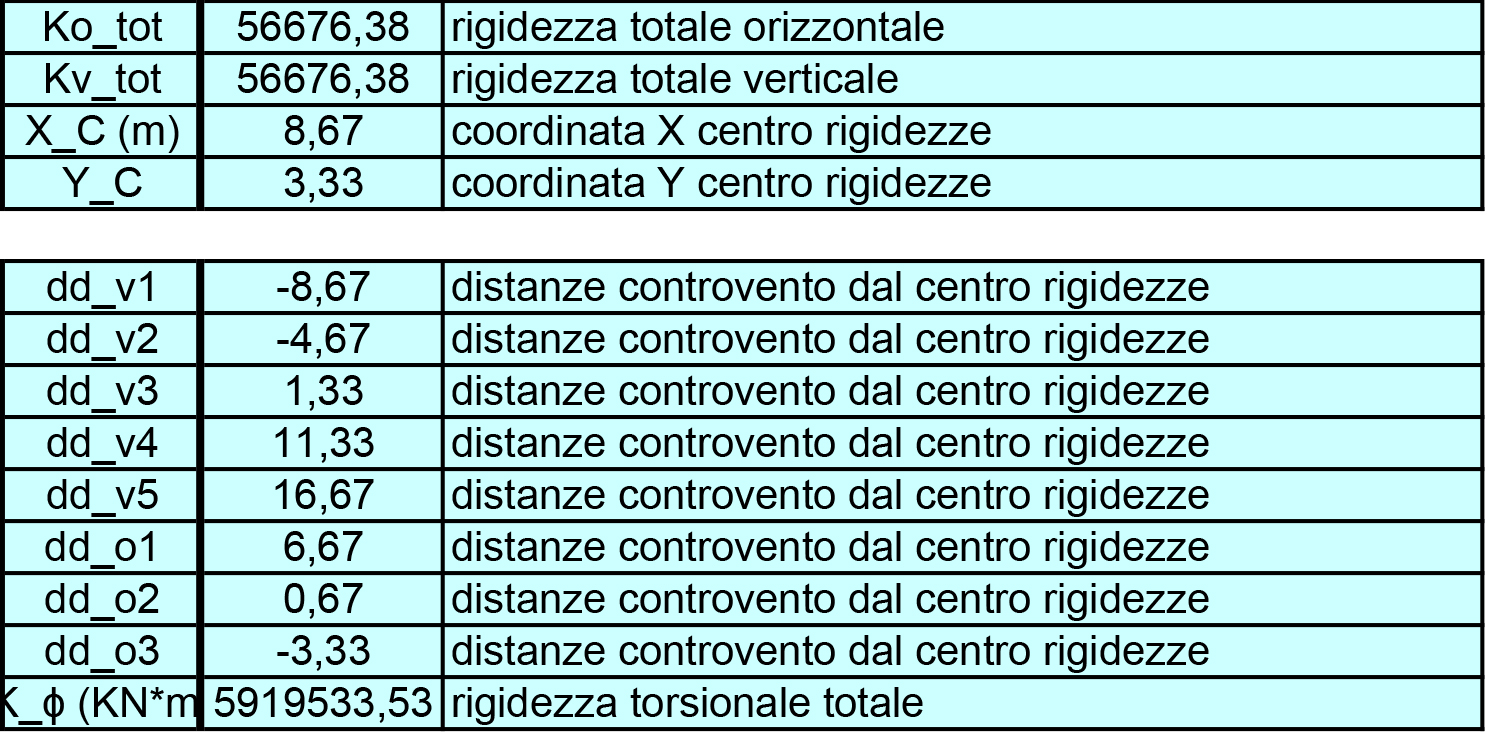
Calcoliamo ora le coordinate del centro di rigidezza, e le distanze di ogni singolo controvento da queste.
Per trovare le coordinate procederemo allo stesso modo, calcolando cioè la sommatoria del prodotto fra le rigidezze di ogni controvento per le rispettive distanze (verticali o orizzontali a seconda della coordinata da trovare) il totale diviso la rigidezza verticale o orizzontale totale.
Grx=∑Kvi*dvi/Kvtot
Gry=∑Koi*doi/Kotot

Infine troviamo la rigidezza torsionale totale:

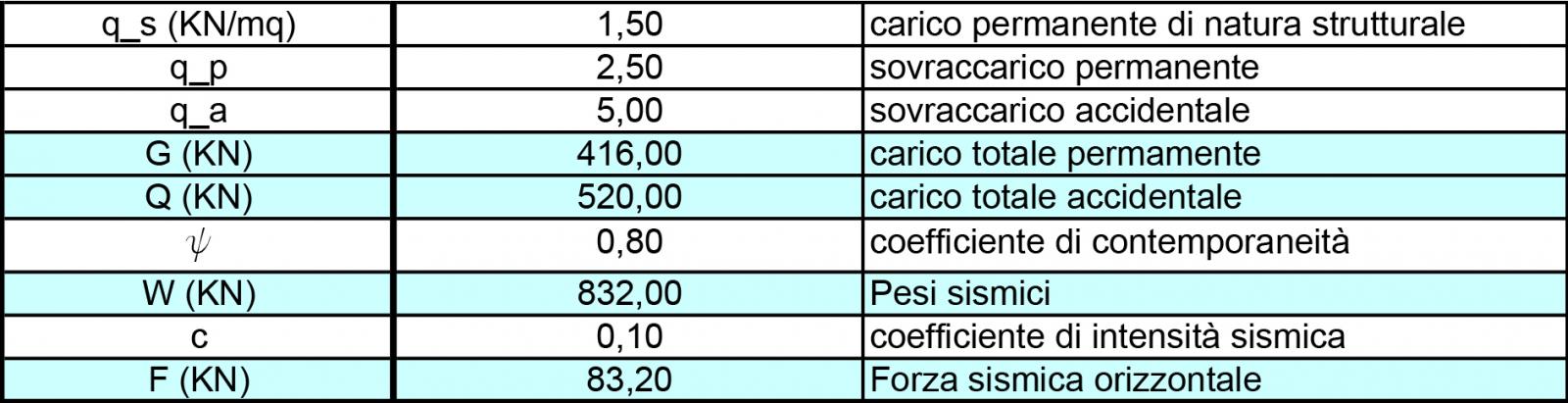
Dalla somma dei carichi strutturali, permanenti e accidentali della struttura (qs, qp e qa), calcoliamo i carichi sismici e ripartiamoli lungo gli assi X e Y per ogni controvento.

Ripartizione forza sismica lungo X:

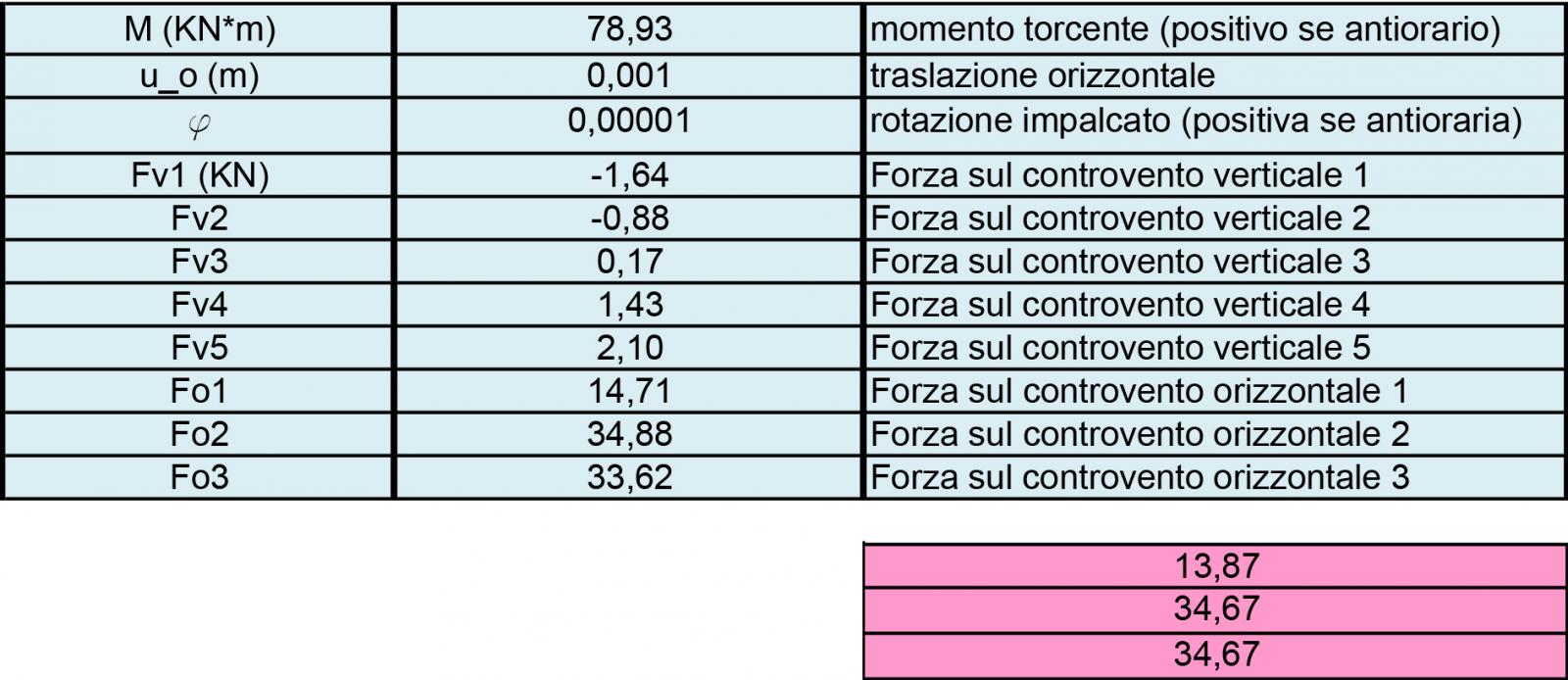
Ripartizione forza sismica lungo Y:

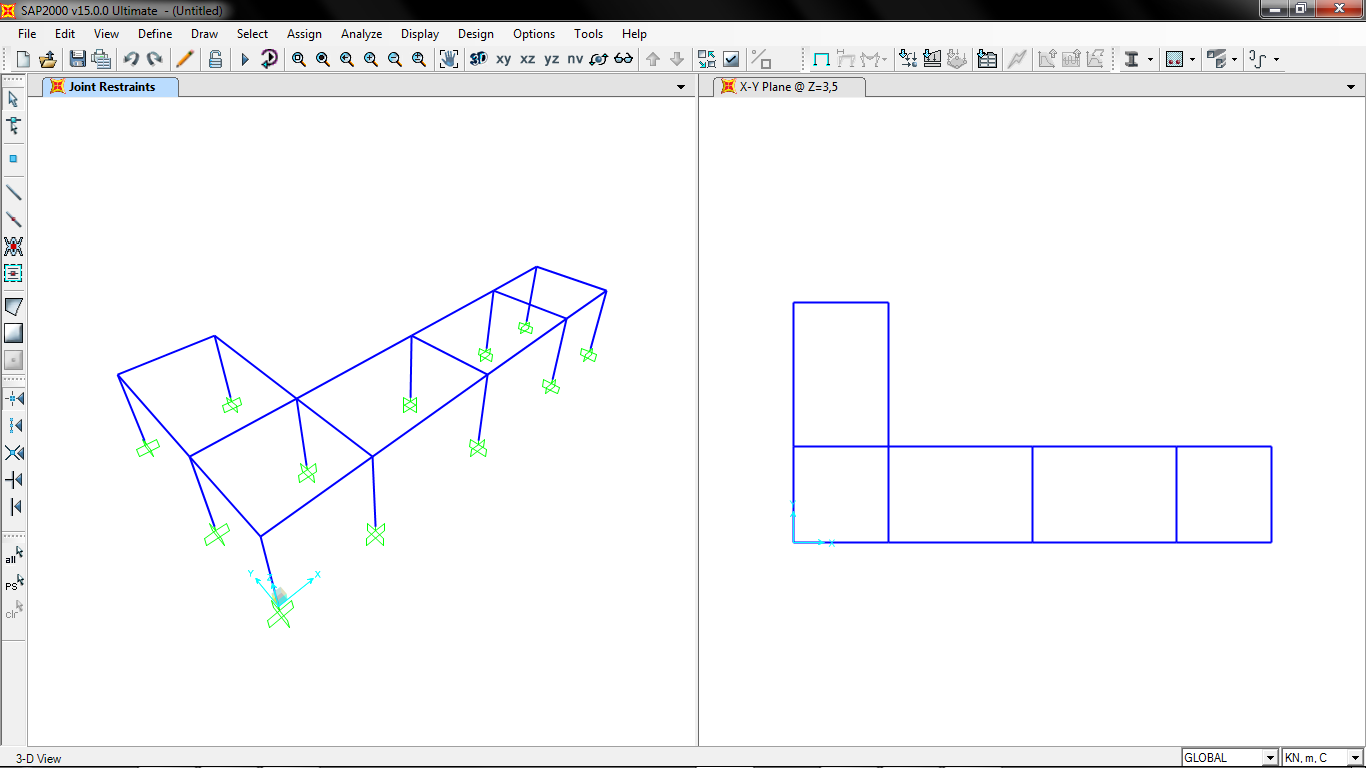
Procediamo ora importando l’impalcato su SAP e incastriamo tutti i pilastri a terra:

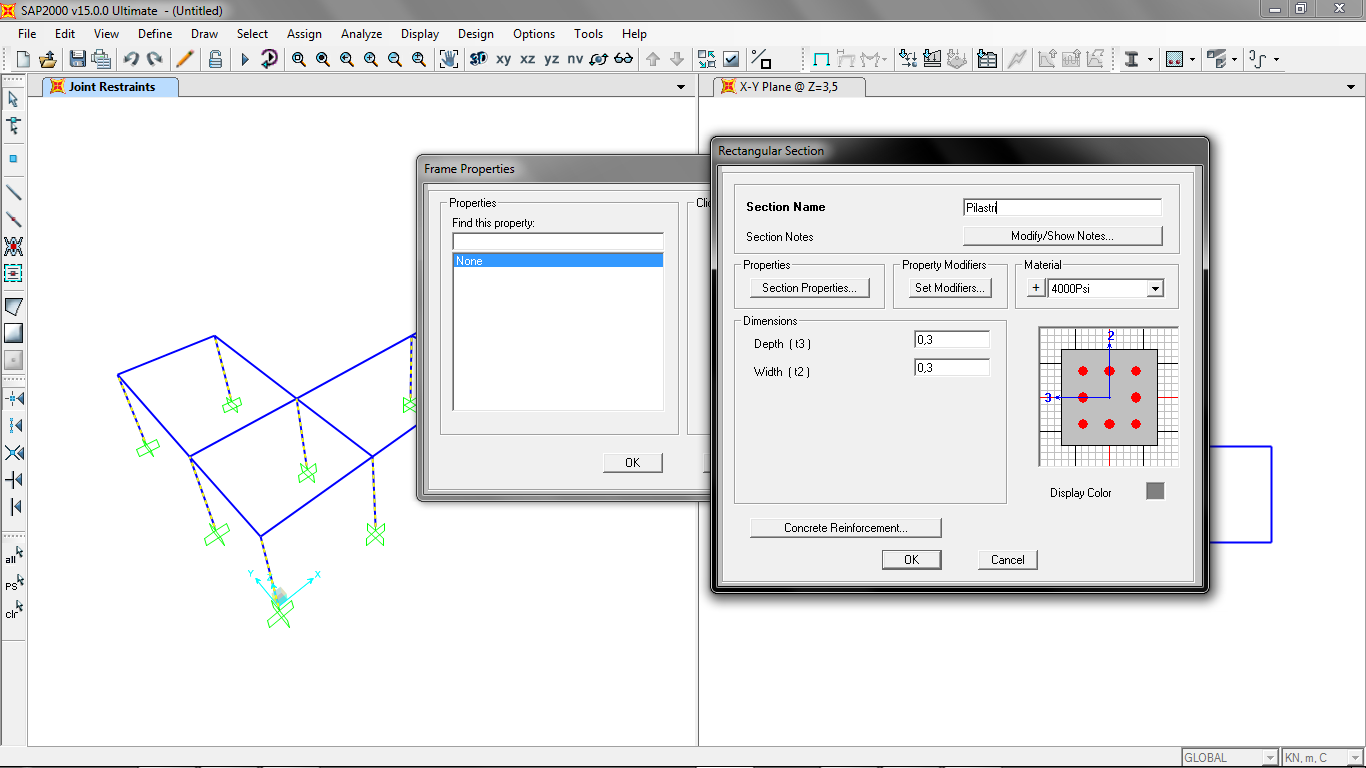
Assegniamo ad ogni pilastro la sua sezione/materiale (assign/frame/frame section), utilizzando la nostra sezione 30x30 in Concrete.

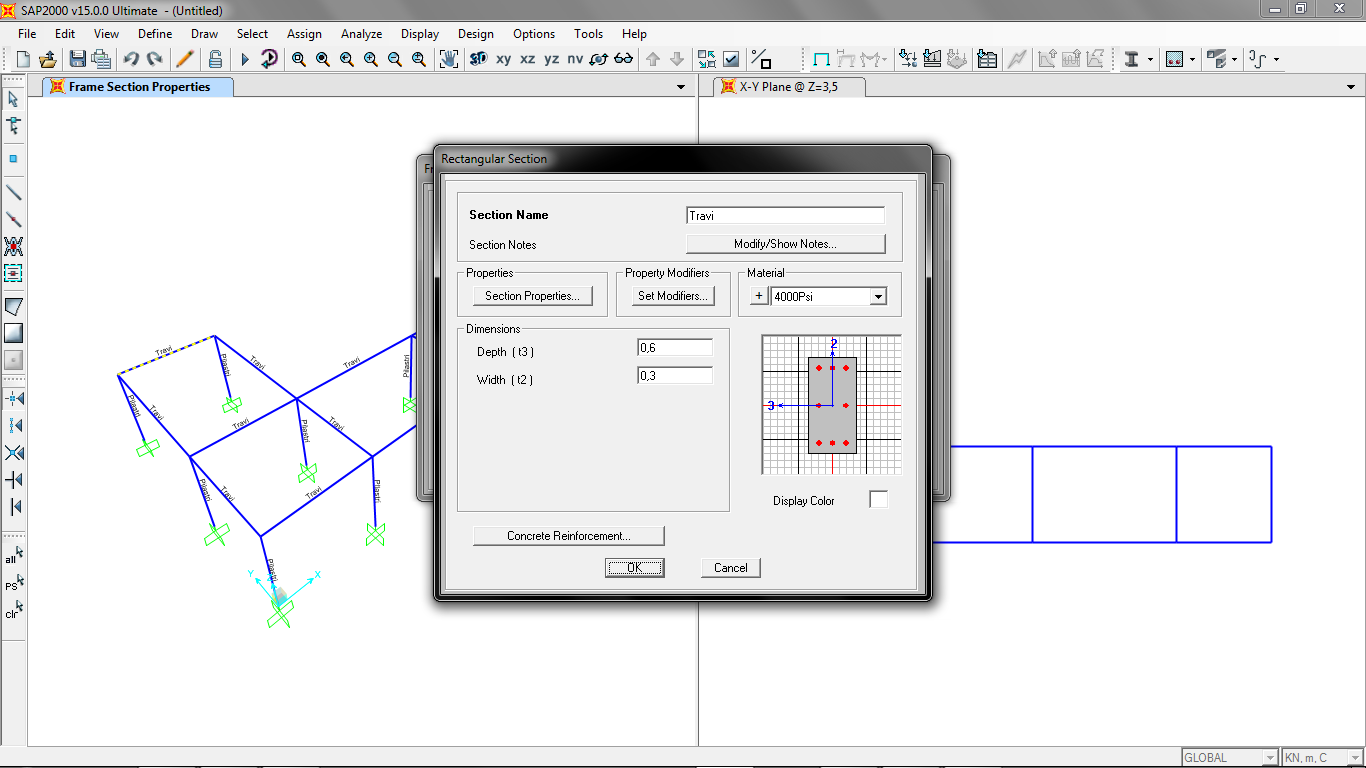
Stesso procedimento con le travi, ma di sezione 30x60:

Disegniamo ora il centro delle rigidezze precedentemente calcolato:

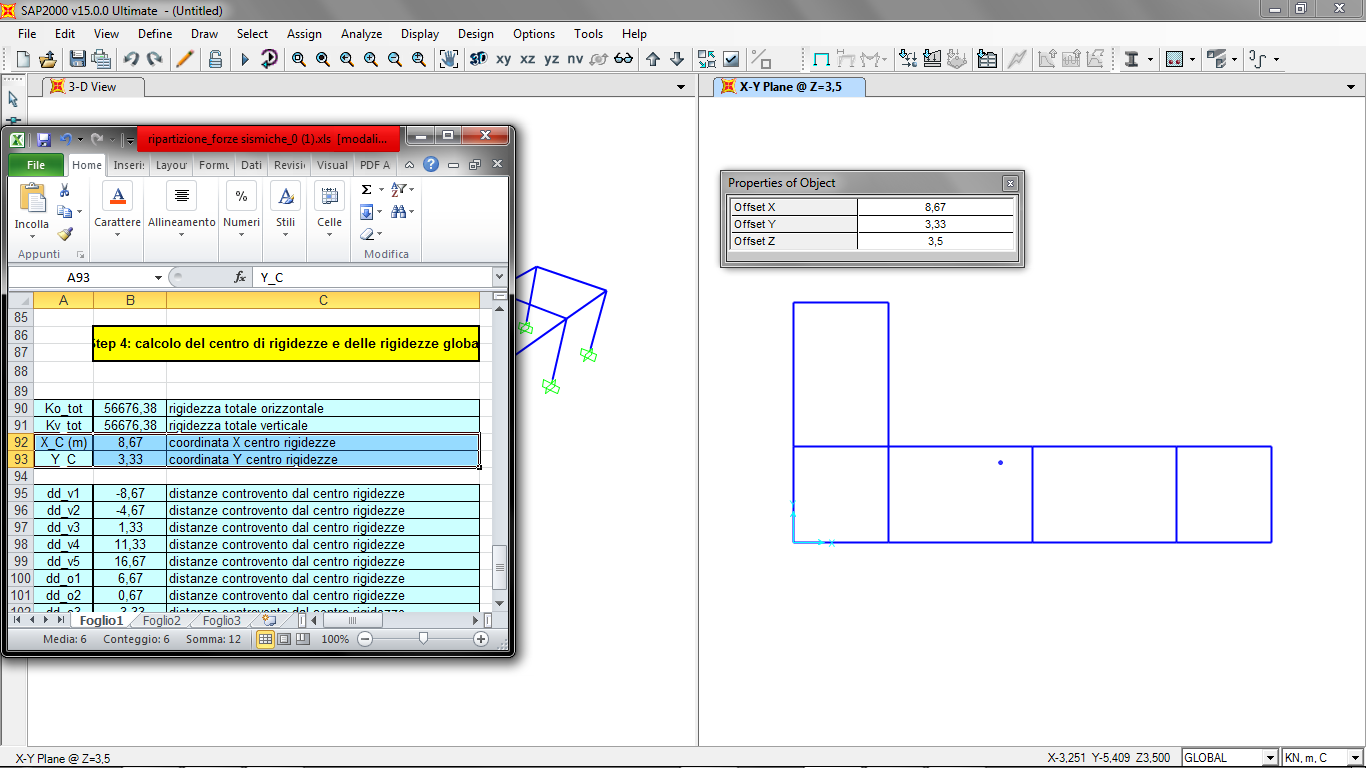
Rendiamo rigida la struttura, comprensiva del centro di rigidezze, in modo tale da far spostare tutto insieme, anche se il punto è esterno.
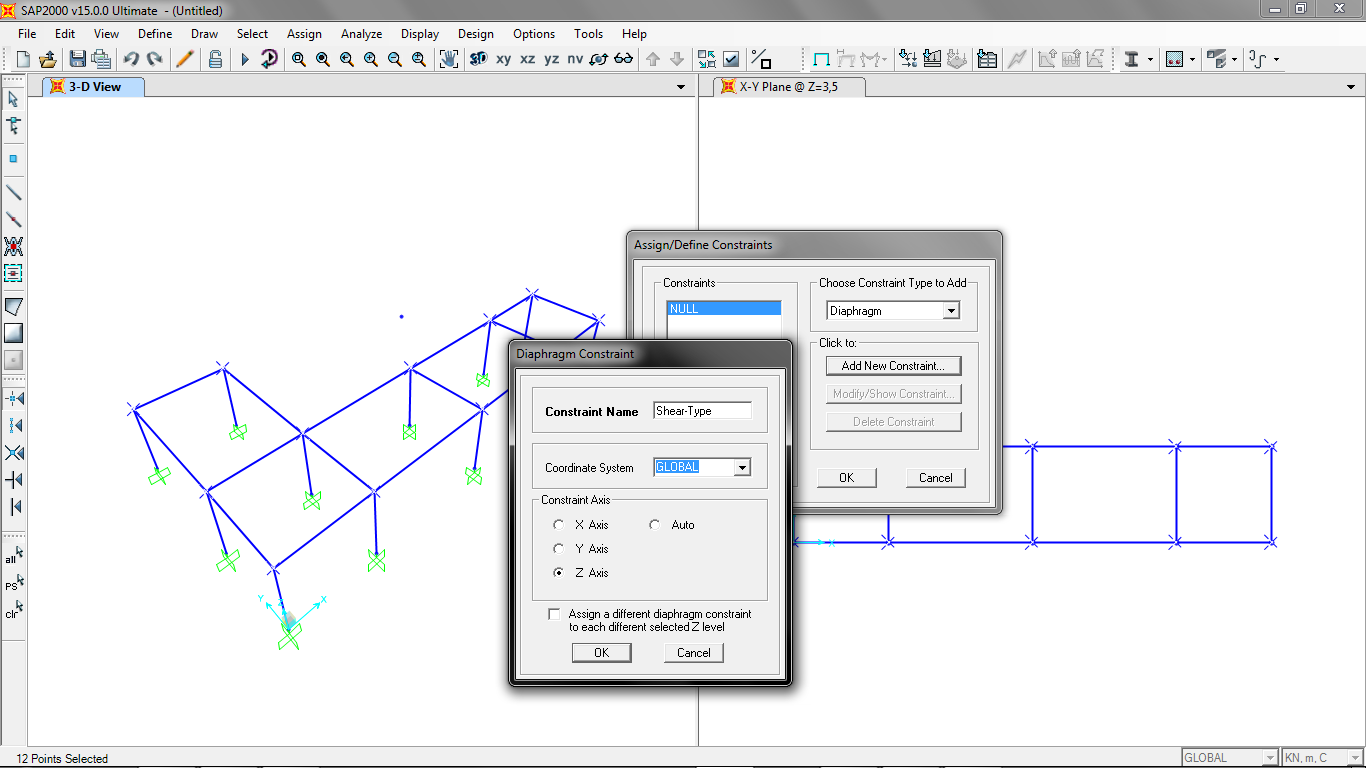
Per fare ciò selezioniamo tutti i nodi trave/pilastro e il centro delle rigidezze, andiamo su Assign/Joint/Constraint e selezioniamo Diaphragm.

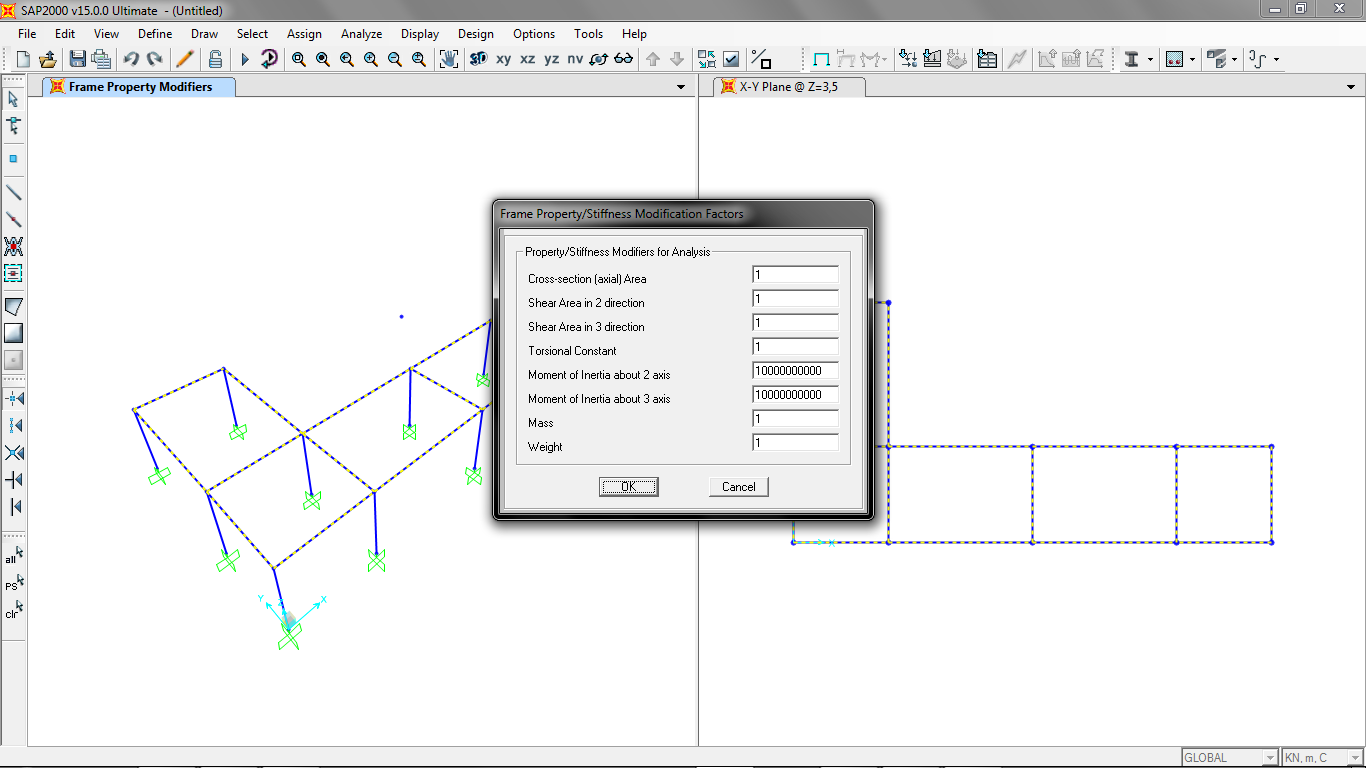
Dato che come abbiamo detto, stiamo usando un telaio Shear-Type, dobbiamo rendere indeformabili le travi. Per farlo possiamo andare su Frame Property e inserire un momento di inerzia molto alto.

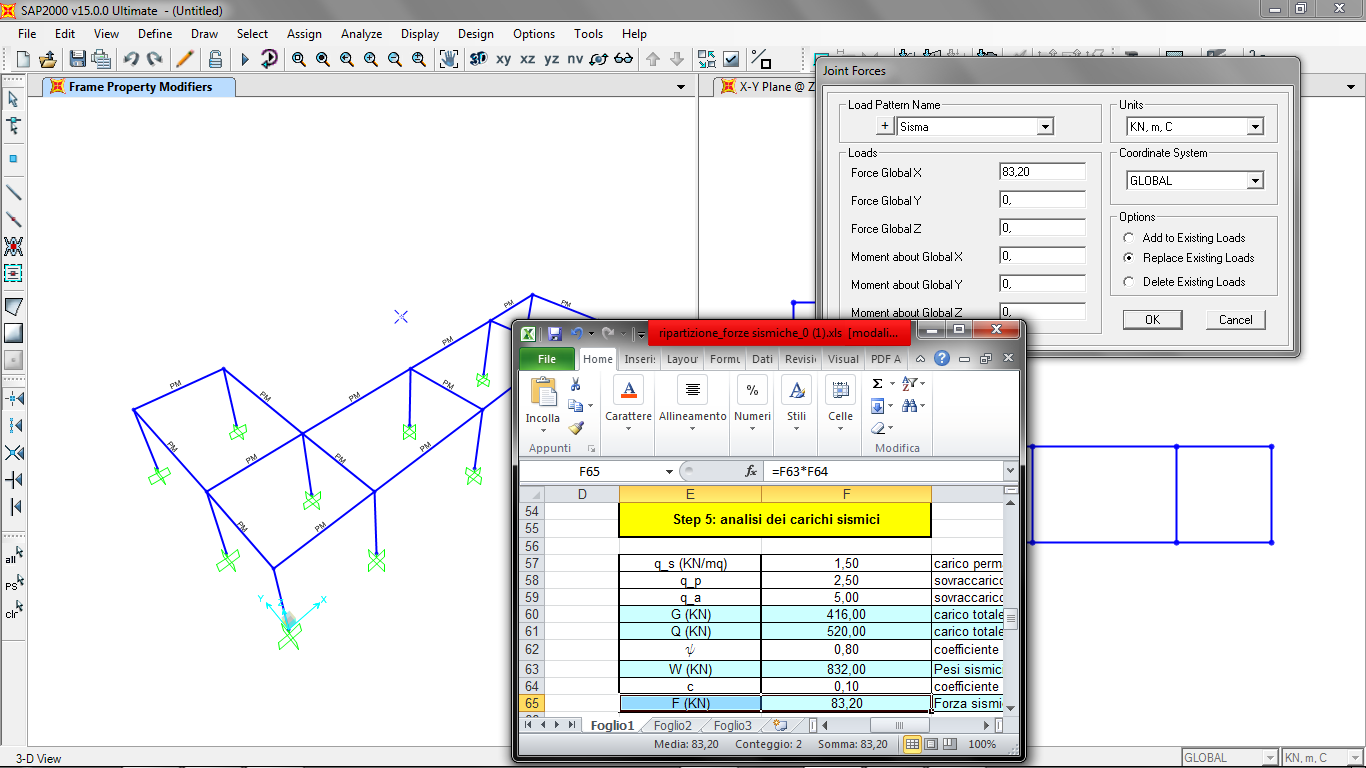
Selezioniamo ora il centro delle rigidezze e applichiamo la forza sismica lungo l’asse X del valore calcolato con l’algoritmo di Excel.

Andiamo a calcolare la deformazione:

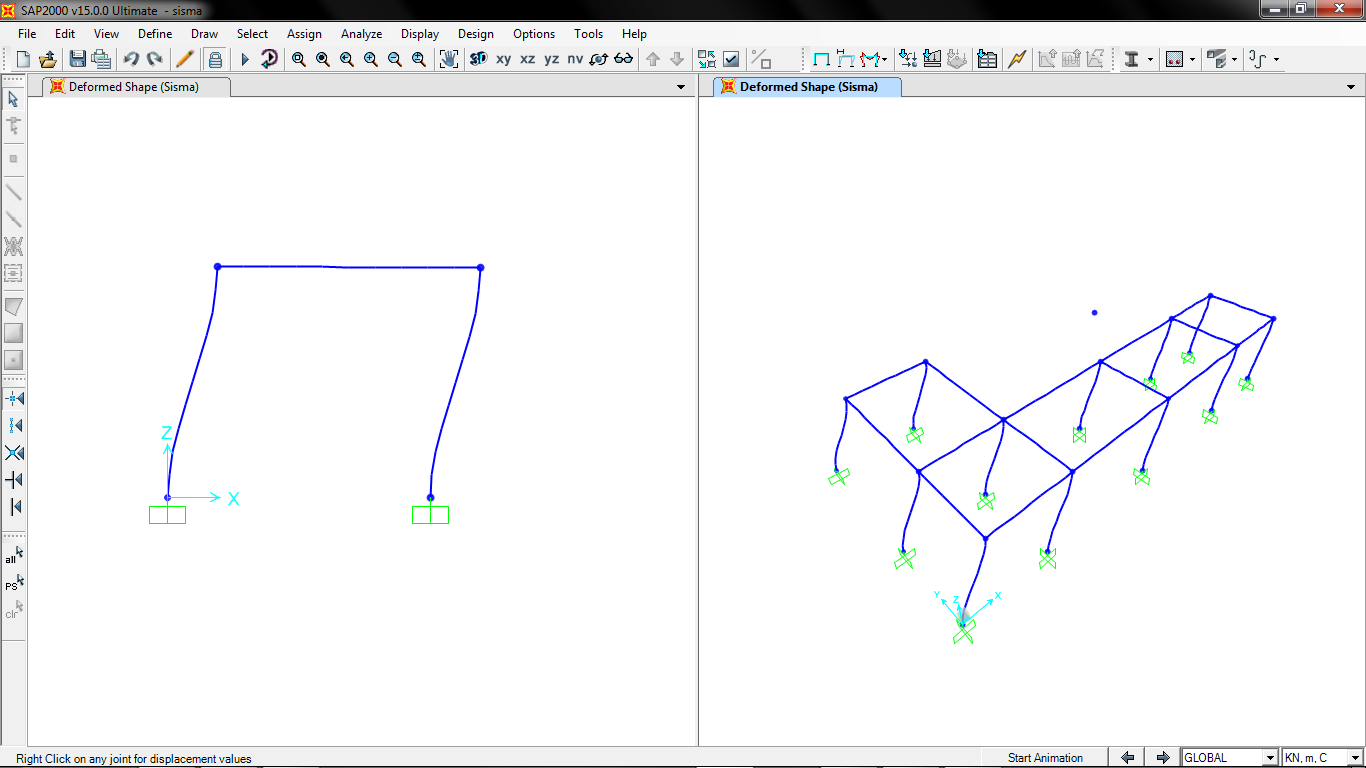
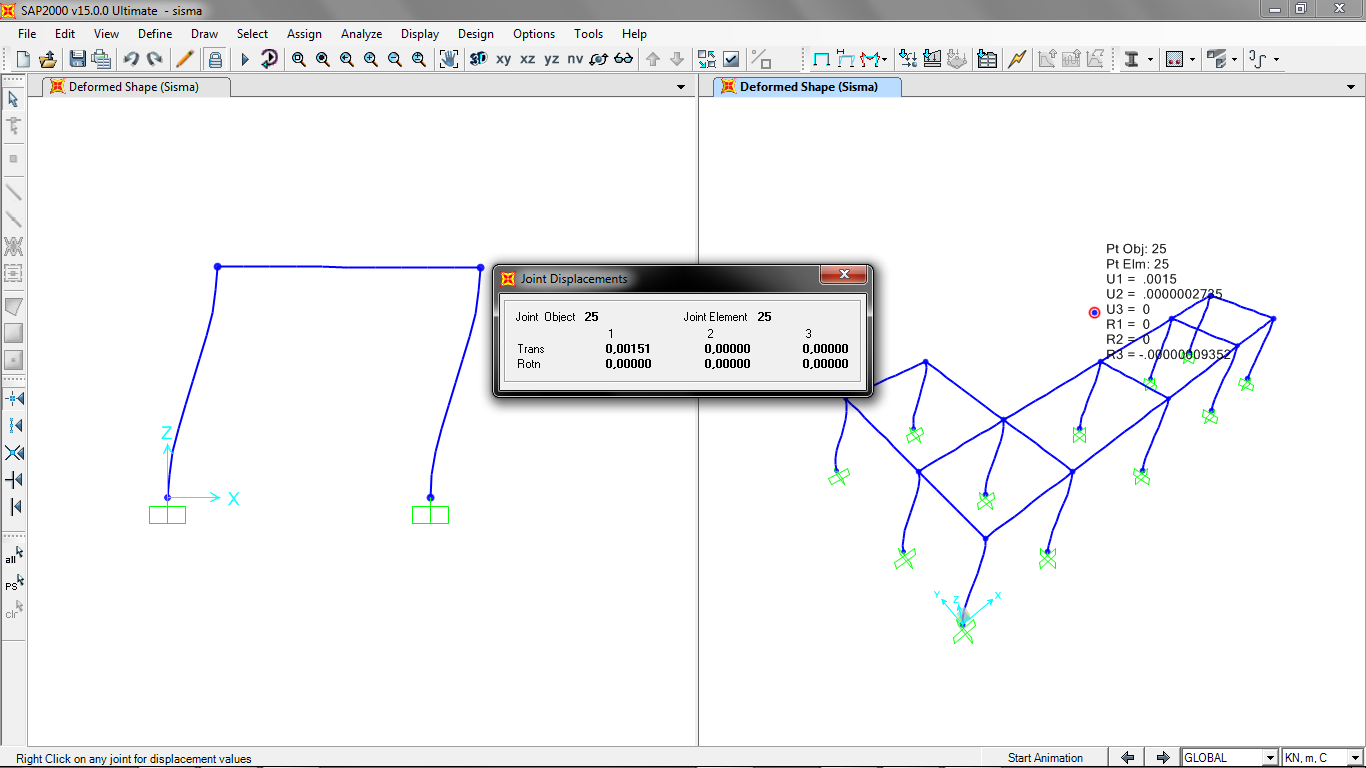
Possiamo notare come il centro delle rigidezze non venga sottoposto a rotazione ma solo a traslazione:

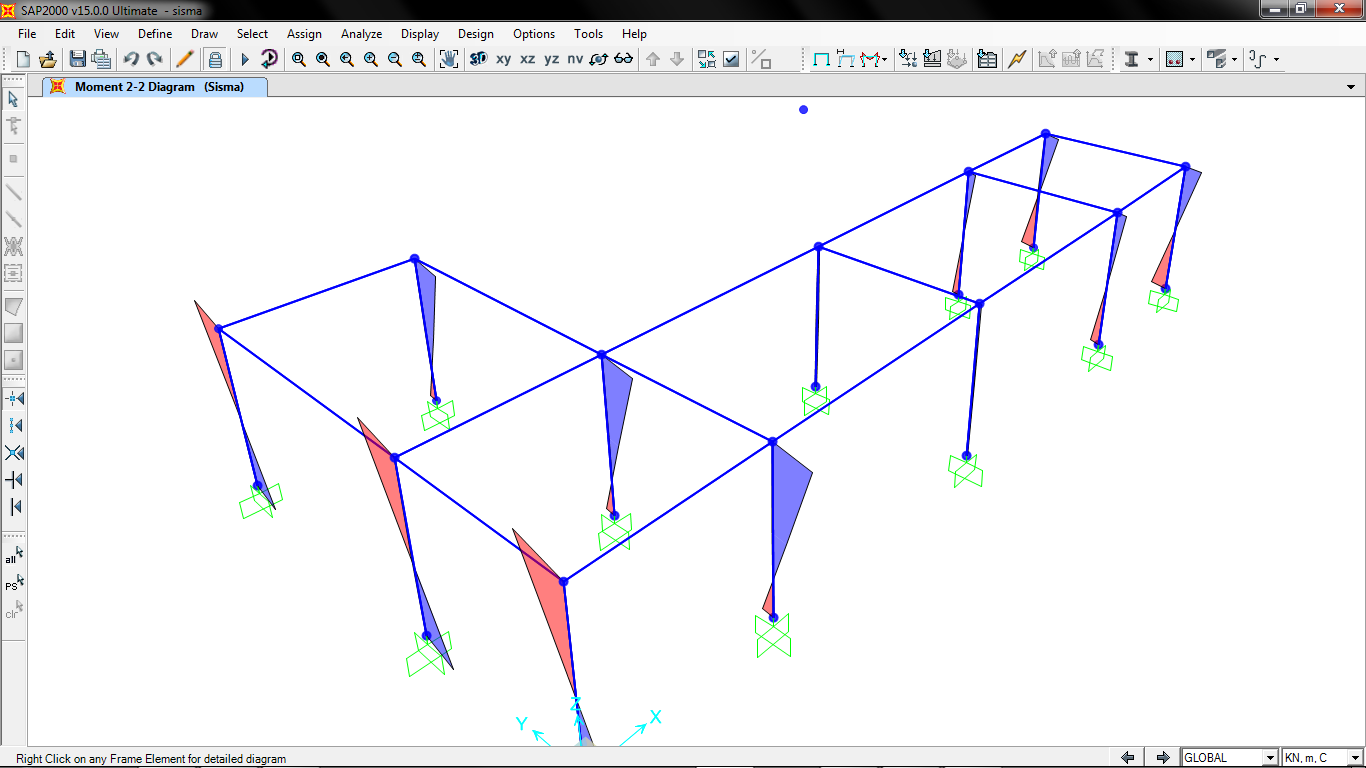
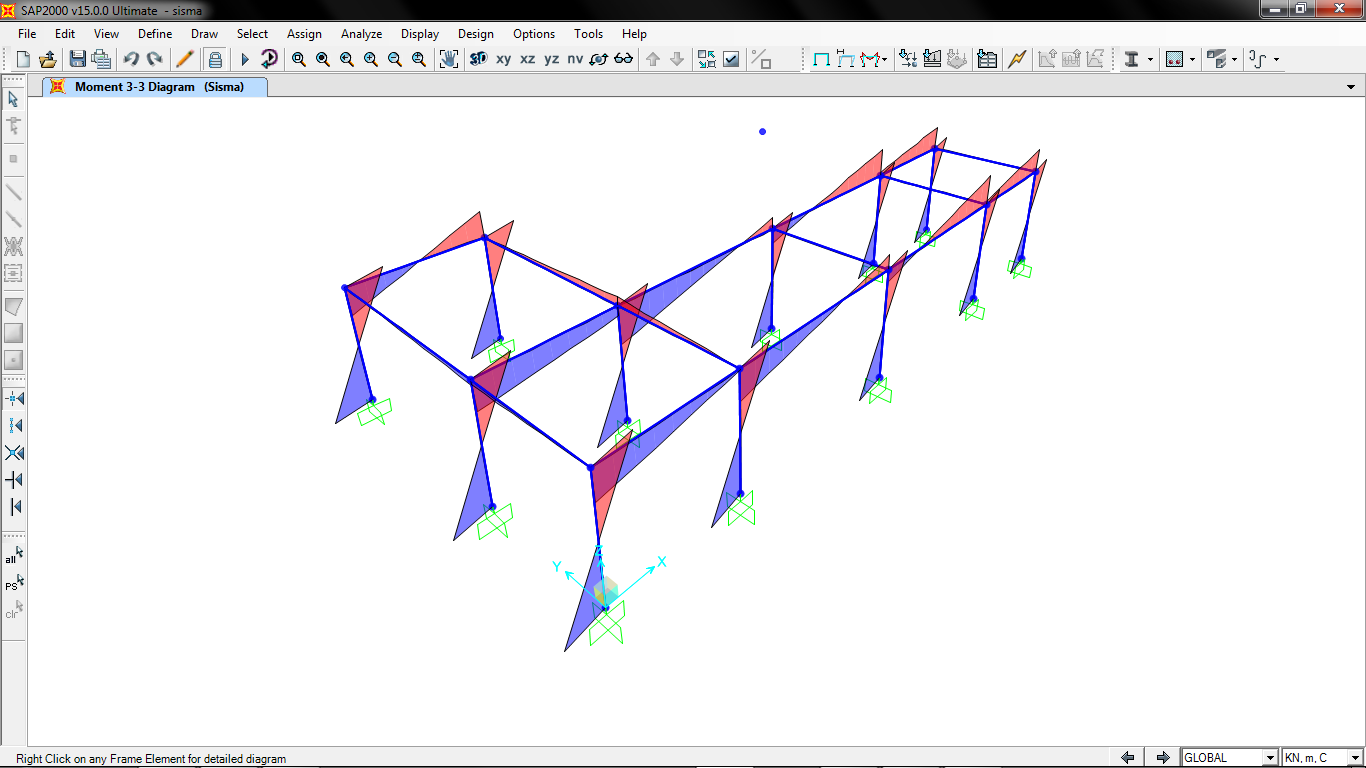
Andiamo infine a calcolare rispettivamente il momento 2-2 e il momento 3-3 della struttura.