blog di MARCO.CRISTOFORI

Per questa esercitazione ci viene richiesto di andare a risolvere una struttura ad arco con il software SAP.
Questo tipo di struttura, reagisce grazie alla propria geometria e tende a lavorare solo con sforzo normale, quindi in maniera omogenea su tutta la sezione, avendo così un’ottimizzazione del materiale (nel momento per esempio, le fibre al centro della sezione lavorano meno rispetto quelle esterne).
Data l’impossibilità di utilizzare il programma per disegnare linee curve, utilizzeremo un programma CAD (autoCAD, Rhino, etc.).
Una volta esportato il file (.dxf, .iges) importiamolo sul programma SAP.
Svolgiamo prima il caso dell’arco a tutto sesto, ovvero quando la freccia è pari a metà della luca (semicircolare), dimostrando che tra le reazioni vincolari (appoggiato-appoggiato) risulteranno anche azioni orizzontali, quindi spingenti lateralmente.
Una volta preso metà arco in considerazione (tenendo conto che il concio di chiave è rappresentabile come una cerniera interna), possiamo dimostrare come la reazione verticale sull’appoggio risulterà uguale a metà carico equamente distribuito sulla proiezione dell’arco (quindi q*l, dove l è metà luce), mentre tramite equilibrio dei momenti dimostriamo come la reazione orizzontale sull’appoggio (verso l’interno) risulterà uguale a ql/2.

Importiamo il disegno su SAP.

Mettiamo i vincoli di appoggio agli estremi.

Andiamo ad inserire una cerniera interna sul concio di chiave.

Applichiamo ora una sezione in cemento armato all’intero arco (ottimizzato già con la stessa sezione su tutta la lunghezza).

Andiamo a togliere il peso proprio della struttura e a applicare un carico distribuito q pari a 10 Kn/m sulla proiezione dell’arco a terra, non sulla lunghezza dell’arco (gravity projected).

Calcoliamo ora le reazioni.

I risultati corrispondono a quelli descritti nell’analisi spiegata sopra.

Analizziamo ora il caso di un arco parabolico, ovvero un arco il cui andamento corrisponde all’andamento di una parabola, quindi di equazione y(x)=ax^2+bx+c.

Dopo averlo disegnato tramite SpLine su autoCAD, importiamo il file su SAP.

Applichiamo i vincoli (appoggio - appoggio).

Applichiamo una cerniera interna nel concio di chiave.

Applichiamo la sezione come nel caso precedente,

e anche il carico distribuito sulla proiezione dell’arco.

Calcoliamo le reazioni vincolari.

Notiamo come mentre la reazione verticale rimane la stessa, l’orizzontale ovviamente sarà diversa, dato che in questo caso, non corrisponde allo sforzo normale.  Tale reazione sarà uguale a ql^2/2f (dove f corrisponde alla freccia dell’arco 6m nel nostro caso).

Proviamo ora ad eliminare le azioni spingenti lateralmente tramite l’addizione di due mensole esterne.
Provando a calcolare manualmente le razione di questa situazione, siamo riusciti a trovare che per eliminare totalmente queste spinte le mensole devono avere una lunghezza, in proiezione sull’asse X pari al prodotto della semiluce e la radice quadrata del rapporto tra carico q sull’arco e carico q sulla mensola:

b=l*sqrt(q1/q2)

Immaginando q1=q2, per eliminare lo sforzo orizzontale avrei dovuto inserire mensole di una lunghezza tale da avere una proiezione sull’asse X di 3m.

Ho riscontrato problemi nell’importazione del file cad, ho quindi disegnato direttamente su SAP le mensole inserendo le coordinate dei punti negli estremi.

Applichiamo ora lo stesso carico distribuito anche sulle mensole, sempre sulla proiezione di queste sull’asse X.

Applichiamo la sezione in cemento armato.

Dato che utilizziamo un carico distribuito agente sulla proiezione della struttura sull’asse orizzontale, l’inclinazione della mensola non influirà sulle reazioni vincolari (ovviamente influirà sulle sollecitazioni e  sulle deformazioni), dimostriamolo utilizzando due mensole di differenti inclinazioni ma uguale proiezione.

Il risultato della reazioni verticali sarà la somma tra q1*l e q2*b, mentre quelle orizzontali saranno uguali a 0 come immaginavamo.
In conclusione è quindi possibile eliminare le spinte orizzontali tramite alcune scelte già in fase progettuale.
 

Andiamo a calcolare il centro delle rigidezze di un impalcato in cemento armato avente 5 telai verticali e 3 orizzontali.
Tale tipo di studio ci porterà a capire meglio il funzionamento di telai non solo sottoposti ad azioni verticali.  Infatti, un telaio, se ben pensato in fase progettuale, può resistere anche alle azioni orizzontali a cui la struttura è sottoposta, quindi agire da vero e proprio controvento.

Disegniamo ora le rigidezze (Kv e Ko) dei singoli telai. Per essere rappresentate useremo un avatar, una molla, che meglio raffigura la reazione alle spinte orizzontali di questi controventi.
Aggiungiamo anche gli assi X e Y, dato che ci servirà un punto di origine su cui fare calcoli di natura geometrica.

Procediamo ora su Excel.
Tramite questo algoritmo è possibile calcolare centro di massa, centro delle rigidezze e ripartizioni delle forze sismiche.
Primo passo, calcolare la rigidezza di ogni singolo controvento. Per fare ciò, necessitiamo modulo di Young (a seconda del materiale), momento di inerzia (che ovviamente varierà in caso vari la sezione) di ogni pilastro, e altezza.
Per il momento di inerzia, data la forma quadrata del pilastro, useremo la formula b^4/12 (b*h^3/12 con h e b uguali).
Dato che il nostro telaio è di tipo Shear-Type la struttura orizzontale è infinitamente rigida e quindi indeformabile assialmente mentre i pilastri sono soggetti a flessione. La trave perciò si muoverà con atto di moto rigido. Dato l’incastro dei pilastri a terra quindi, gli unici spostamenti saranno nella testa del pilastro, e uguali per tutti i pilastri che compongono il singolo telaio. La rigidezza traslante (K) quindi sarà calcolata come:
K=12*E*Itot/h^3

Telai verticali:

Telai orizzontali:

Elenchiamo ora le distanze orizzontali e verticali dei singoli controventi rispetto all’origine:

Suddividiamo ora l’impalcato in figure geometriche semplici di cui possiamo trovare i centri di massa:

Possiamo ora trovare il centro di massa dell’intera struttura. Le coordinate di tale centro possono essere trovate come sommatoria delle distanze dei singoli centri di massa rispetto agli assi (y o x a seconda di ciò che si vuole calcolare) moltiplicate per le rispettive aree e dividendo il totale per l’area complessiva.
Gmx=∑xG*Ai/Atot
Gmy=∑yG*Ai/Atot

Calcoliamo ora le coordinate del centro di rigidezza, e le distanze di ogni singolo controvento da queste.
Per trovare le coordinate procederemo allo stesso modo, calcolando cioè la sommatoria del prodotto fra le rigidezze di ogni controvento per le rispettive distanze (verticali o orizzontali a seconda della coordinata da trovare) il totale diviso la rigidezza verticale o orizzontale totale.
Grx=∑Kvi*dvi/Kvtot
Gry=∑Koi*doi/Kotot

Infine troviamo la rigidezza torsionale totale:

Dalla somma dei carichi strutturali, permanenti e accidentali della struttura (qs, qp e qa), calcoliamo i carichi sismici e ripartiamoli lungo gli assi X e Y per ogni controvento.

Ripartizione forza sismica lungo X:

Ripartizione forza sismica lungo Y:

Procediamo ora importando l’impalcato su SAP e incastriamo tutti i pilastri a terra:

Assegniamo ad ogni pilastro la sua sezione/materiale (assign/frame/frame section), utilizzando la nostra sezione 30x30 in Concrete.

Stesso procedimento con le travi, ma di sezione 30x60:

Disegniamo ora il centro delle rigidezze precedentemente calcolato:

Rendiamo rigida la struttura, comprensiva del centro di rigidezze, in modo tale da far spostare tutto insieme, anche se il punto è esterno.
Per fare ciò selezioniamo tutti i nodi trave/pilastro e il centro delle rigidezze, andiamo su Assign/Joint/Constraint e selezioniamo Diaphragm.

Dato che come abbiamo detto, stiamo usando un telaio Shear-Type, dobbiamo rendere indeformabili le travi. Per farlo possiamo andare su Frame Property e inserire un momento di inerzia molto alto.

Selezioniamo ora il centro delle rigidezze e applichiamo la forza sismica lungo l’asse X del valore calcolato con l’algoritmo di Excel.

Andiamo a calcolare la deformazione:

Possiamo notare come il centro delle rigidezze non venga sottoposto a rotazione ma solo a traslazione:

Andiamo infine a calcolare rispettivamente il momento 2-2 e il momento 3-3 della struttura.

Facendo riferimento alla seconda esercitazione (ovvero dimensionamento di una trave, appoggiata-appoggiata in cls, in legno e in acciaio), andiamo a dimensionare una trave a sbalzo. Per meglio capire le differenze meccaniche tra una trave appoggiata-appoggiata e una trave a sbalzo in termini numerici, useremo lo stesso interasse e gli stessi pacchetti murari, in tal modo, a fine esercitazione, potremo tirare le somme.
L'interasse, quindi è di 4 metri, mentre la luce (6 metri nell'ultima esercitazione) sarà di 4 metri.

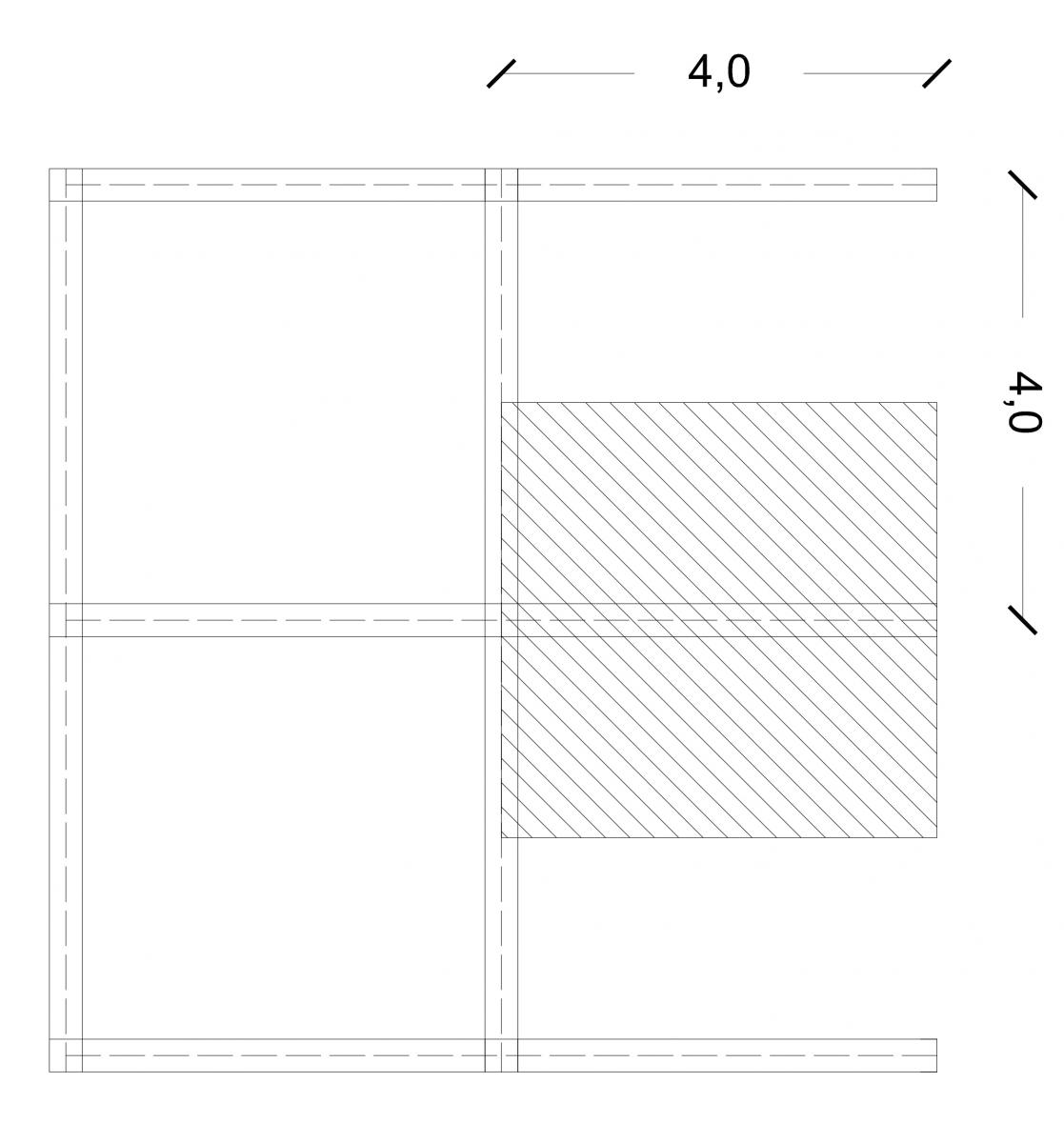
SOLAIO IN LEGNO

Al fine di ricordare, andremo a riscrivere il calcolo per trovare i carichi esercitati dal solaio cambiando ovviamente la luce da 6 a 4 metri.

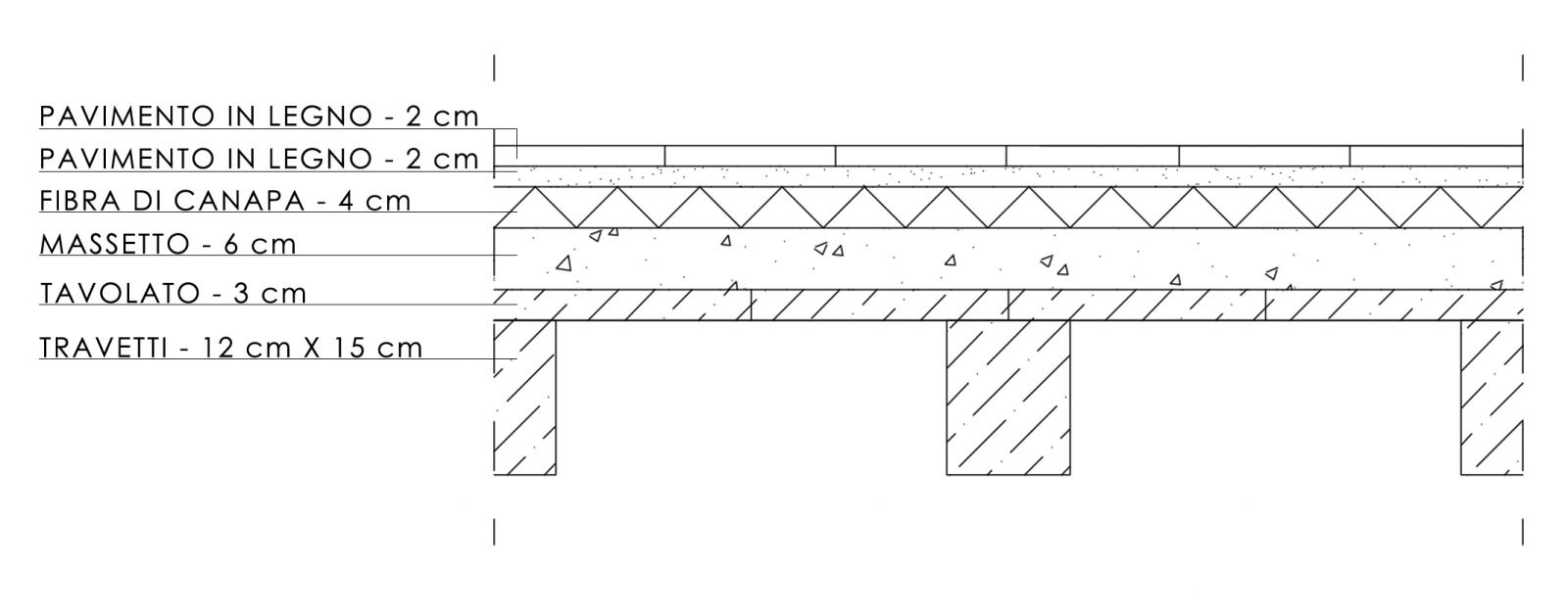
Carichi Strutturale (qs)

-Tavolato in pioppo:
0,03m X 1,00m X 1,00m X 6,00KN/mc / 1,00mq= 0,18 KN/mq
-Travetti in pioppo:
 0,12m X 0,15m X 1,00m X 6,00KN/mc X 2(numero travetti in un metro lineare) / 1,00mq= 0,22 KN/mq

TOTALE: 0,40 KN/mq

Carichi Permanenti (qp)

-Pavimento in pioppo:
0,02m X 1,00m X 1,00m X 6,00KN/mc / 1,00mq= 0,12 KN/mq
-Malta di allettamento:
0,02m X 1,00m X 1,00m X 21,00KN/mc / 1,00mq= 0,42 KN/mq
-Fibra di canapa:
0,04m X 1,00m X 1,00m X 2,60KN/mc / 1,00 mq= 0,10 KN/mq
-Massetto (calcestruzzi leggeri):
0,06m X 1,00m X 1,00m X 14KN/mc / 1,00 mq= 0,84 KN/mq
-Tramezzi: 1,00 KN/mq
-Impianti: 0,50 KN/mq

TOTALE: 2,98 KN/mq

Carichi Accidentali (qa)

-2 KN/mq

I carichi ora andranno moltiplicati per dei coefficienti di sicurezza, nel nostro caso 1,30 per carichi strutturali e permanenti, 1,50 per carichi accidentali.

Per calcolare il momento massimo (ql^2/8 per la prima esercitazione, mentre per una soletta a sbalzo ql^2/2) abbiamo bisogno del carico distribuito al metro lineare (q), calcolabile con i dati che abbiamo.

Scegliamo un’altezza di progetto, calcoliamo il peso della trave e verifichiamo la resistenza di quest’ultima.

Ora possiamo procedere al calcolo e alla verifica della deformabilità. Per fare ciò abbiamo bisogno del modulo di Young e del momento di inerzia (che data la sezione rettangolare sarà facilmente calcolabile, b*h^3/12). Lo spostamento massimo all’estremo non vincolato dello sbalzo sarà uguale a q*l^4/8E*I.

Calcolato lo spostamento massimo, andiamo a verificare tenendo in conto che questo deve essere minore a 1/250 della luce, quindi il rapporto luce/spostamento massimo, dovrà essere superiore a 250.
In questo caso con una sezione 30cm X 70cm la trave in legno è verificata.

SOLAIO IN CLS ARMATO

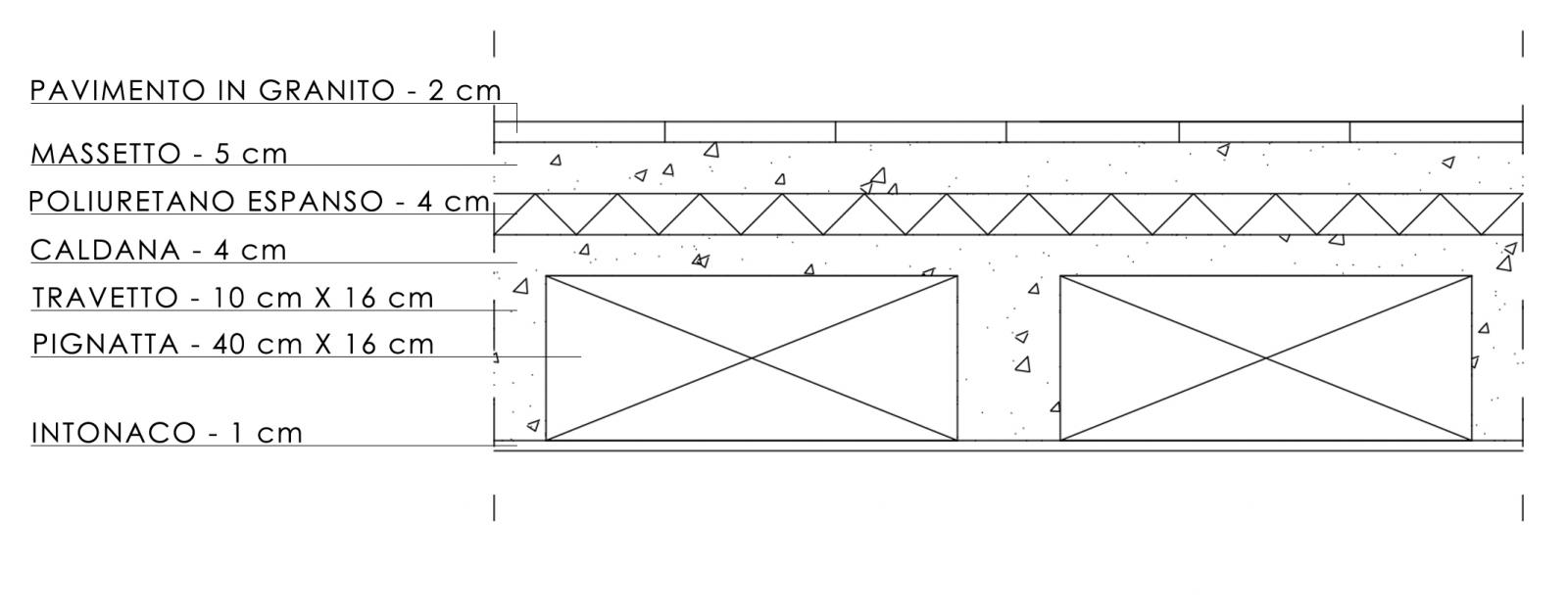
Carichi Strutturale (qs)

-Getto in CLS:
0,04m X 1,00m X 1,00m X 25KN/mc / 1,00mq= 1KN/mq
-Travetti:
0,10m X 0,16m X 1,00m X 25KN/mc X 2(numero travetti in un metro lineare)  / 1,00mq= 0,80KN/mq

TOTALE: 1,80 KN/mq

Carichi Permanenti (qp)

-Pavimento in granito:
0,02m X 1,00m X 1,00m X 27KN/mq / 1,00mq= 0,54 KN/mq
-Massetto (calcestruzzi leggeri):
0,05m X 1,00m X 1,00m X 14,00KN/mc / 1,00 mq= 0,70 KN/mq
-Poliuretano espanso:
0,04m X 1,00m X 1,00m X 0,35KN/mc / 1,00mq= 0,01 KN/mq
-Pignatte:
0,16m X 0,40m X 1,00m X 5,00 KN/mc X2 (numero di pignatte in un metro lineare) / 1,00mq =0,64 KN/mq
-Tramezzi:1,00 KN/mq
-Impianti: 0,50 KN/mq

TOTALE: 3,39 KN/mq

Carichi Accidentali (qa)

-2 KN/mq

Per calcolare le sigma (sig_fa e sig_ca), abbiamo dovuto inserire dei dati riguardanti le caratteristiche dei materiali:
-per l’acciaio necessitiamo la tensione caratteristica di snervamento (l’armatura deve resistere a trazione) fy. Scegliamo una classe B450A con un limite di snervamento di 450MPa e dividiamolo per il coefficiente parziale di sicurezza relativo all’acciaio (1.15).
-per il calcestruzzo invece abbiamo bisogno della resistenza caratteristica cilindrica a compressione del calcestruzzo a 28 giorni Rck (nel nostro caso C40/50) per moltiplicarla per un fattore di riduttivo per le resistenze a lunga durata  (0,85). Il risultato andrà diviso per ilcoefficiente parziale di sicurezza relativo al calcestruzzo (1,5).

Aggiungiamo l’ultimo dato delta, ovvero l’altezza del copriferrro.
Decidiamo quindi l’altezza di progetto. Sapendo che la minima richiesta è di 41,84 cm e aggiungendo un copriferro di 5 cm potremmo prendere un’altezza di 50 cm.

Anche in questo caso possiamo procedere con la verifica aggiungendo modulo di Young e momento di inerzia.

Notiamo come, nonostante la trave abbia una sezione che verifichi il momento massimo, non è sufficientemente alta per superare la verifica a deformabilità, aggiungiamo quindi 5 cm di altezza, in modo tale da avere un modulo di inerzia maggiore, e poter verificare la trave.

La sezione scelta è di 30cm X 55cm.

SOLAIO IN ACCIAIO

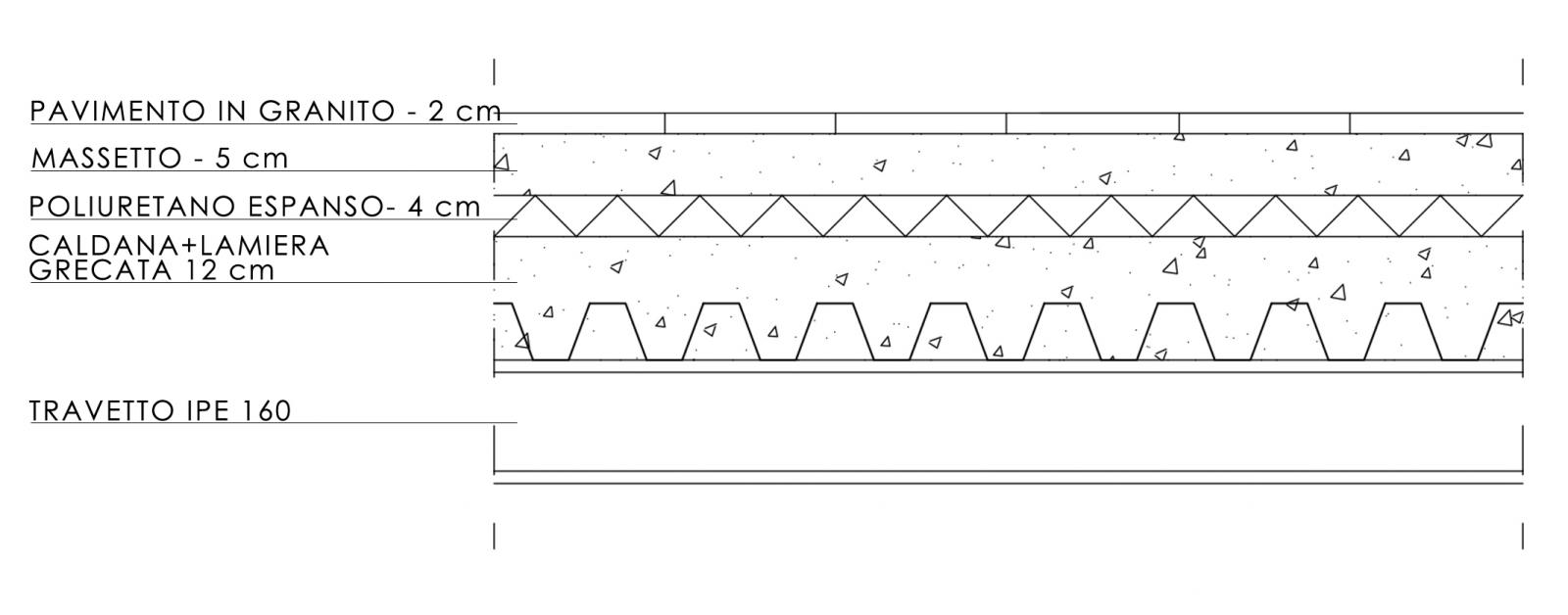
Carichi Strutturale (qs)

-Lamiera Grecata + Soletta CLS (A55/P600):
2,40KN/mq
-Travetto IPE160:
0,158KN/mq X 2(numero travetti in un metro lineare) = 0,316KN/mq

TOTALE: 2,558 KN/mq

Carichi Permanenti (qp)

-Pavimento in granito:
0,02m X 1,00m X 1,00m X 27KN/mq / 1,00mq= 0,54 KN/mq
-Massetto (calcestruzzi leggeri):
0,05m X 1,00m X 1,00m X 14,00KN/mc / 1,00 mq= 0,70 KN/mq
-Poliuretano espanso:
0,04m X 1,00m X 1,00m X 0,35KN/mc / 1,00mq= 0,01 KN/mq
-Tramezzi:1,00 KN/mq
-Impianti: 0,50 KN/mq

TOTALE: 2.75 KN/mq

Carichi Accidentali (qa)

-2 KN/mq

Possiamo ora calcolare il momento.
Per determinare la sigma abbiamo bisogno della resistenza caratteristica fy,k, che ovviamente varia a seconda della tipologia di acciaio scelto. Nel nostro caso classe Fe 430/S275 con una resistenza di 275 Mpa.
Dalla resistenza caratteristica calcolata Wx (975,53cmc) prendiamo una trave IPE400 con resistenza 1160 cmc.

Anche qui, con la prima trave (IPE400), la sezione era sufficiente a resistere al momento, ma non abbastanza per verificare la deformabilità. Abbiamo quindi preso una IPE450.
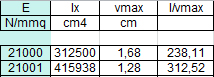
Anche qui per il calcolo della deformazione necessitiamo del modulo di Young e momento di inerzia. Non essendo una sezione rettangolare, il momento di inerzia andrà preso dalla tabella.

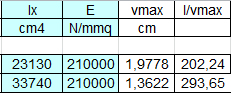
La sezione quindi definitiva è una IPE450.

TIRIAMO LE SOMME!

(Come abbiamo detto, i pacchetti dei solai rimarranno uguali per entrambi i casi)

Con una trave appoggiata-apopggiata, luce 6 metri e interasse 4 metri abbiamo una trave in legno di 30cm X 50cm. Con uno sbalzo di 4 metri invece 30cm X 70cm.

Per il cls invece, appoggio-appoggio, 30cm X 45cm, sbalzo 30cm X 55cm.

Infine, per una trave in acciaio, nel primo caso basterà una IPE300 mentre per lo sbalzo un IPE450.

Nel primo caso comunque, non abbiamo tenuto conto della deformabilità e in più, alcune travi sono sovradimensionate, ma comunque è chiara la forte differenza tra il ql^2/8 e il ql^2/2 dello sbalzo!
 

Andiamo a dimensionare una trave partendo dalle analisi di carico di un solaio da noi scelto.
Svolgeremo 3 tipi di analisi: per una struttura in legno, una in calcestruzzo armato e una in acciaio.
L’area di influenza in questo caso è di 24 mq (interasse 4 m e luca 6 m).

Dobbiamo ora sommare tutti i carichi che gravano sulla trave scelta:
-carichi strutturali (qs): ovvero il peso di tutto ciò che appartiene alla struttura, la trave principale, per il dimensionamento, sarà ovviamente esclusa.
-carichi permanenti (qp): ovvero il peso di tutto ciò che non appartiene alla struttura, comprensivo di tramezzi e impianti.
-carichi accidentali (qa): che dipendono dalla destinazione d’uso e tengono conto di eventi prevedibili ma non continui (per edifici ad uso residenziale 2Kn/mq).

Tali carichi sono al metro quadrato, ciò significa che di ogni elemento che compone il solaio, andremo a moltiplicare  il peso specifico (Kn/mc) per il volume (mc), dividendo poi per una superficie di 1mq.
Per le parti del solaio non distribuite in maniera omogenea (vedi travetti), calcoleremo il peso del singolo per poi moltiplicarlo per il numero di volte che tale elemento apparirà nell’area in esame e diviso per la stessa superficie (1mq).

SOLAIO IN LEGNO

Carichi Strutturale (qs)

-Tavolato in pioppo:
0,03m X 1,00m X 1,00m X 6,00KN/mc / 1,00mq= 0,18 KN/mq
-Travetti in pioppo:
 0,12m X 0,15m X 1,00m X 6,00KN/mc X 2(numero travetti in un metro lineare) / 1,00mq= 0,22 KN/mq

TOTALE: 0,40 KN/mq

Carichi Permanenti (qp)

-Pavimento in pioppo:
0,02m X 1,00m X 1,00m X 6,00KN/mc / 1,00mq= 0,12 KN/mq
-Malta di allettamento:
0,02m X 1,00m X 1,00m X 21,00KN/mc / 1,00mq= 0,42 KN/mq
-Fibra di canapa:
0,04m X 1,00m X 1,00m X 2,60KN/mc / 1,00 mq= 0,10 KN/mq
-Massetto (calcestruzzi leggeri):
0,06m X 1,00m X 1,00m X 14KN/mc / 1,00 mq= 0,84 KN/mq
-Tramezzi: 1,00 KN/mq
-Impianti: 0,50 KN/mq

TOTALE: 2,98 KN/mq

Carichi Accidentali (qa)

-2 KN/mq

I carichi ora andranno moltiplicati per dei coefficienti di sicurezza, nel nostro caso 1,30 per carichi strutturali e permanenti, 1,50 per carichi accidentali.

Per calcolare il momento massimo (ql^2/8) abbiamo bisogno del carico distribuito al metro lineare (q), calcolabile con i dati che abbiamo.

Per calcolare la sigma, abbiamo dovuto inserire dei dati riguardanti le caratteristiche del materiale:
-fm,k: la resistenza a flessione caratteristica (moltiplicata per il coefficiente parziale di sicurezza γ, 1,45 per legno lamellare incollato. Scegliamo la classe GL 24h.
-kmod: coefficiente che tiene conto dell’umidità e dell’effetto dei carichi nel tempo.

Una volta impostata come base 30cm dal risultato ottenuto, 44,84cm, prendiamo come altezza 50,00 cm e procediamo alla verifica aggiungendo il peso proprio della trave.

qtrave= 0,30m X 0,50m X 1,00m X 6,00KN/mc / 4,00m (interasse, per trovare il peso al metro lineare)= 0,22Kn/mq

Sommiamo il peso ai carichi strutturali prima analizzati e verifichiamo.

Con la sezione scelta 30X50 la trave è verificata.

SOLAIO IN CLS ARMATO

Carichi Strutturale (qs)

-Getto in CLS:
0,04m X 1,00m X 1,00m X 25KN/mc / 1,00mq= 1KN/mq
-Travetti:
0,10m X 0,16m X 1,00m X 25KN/mc X 2(numero travetti in un metro lineare)  / 1,00mq= 0,80KN/mq

TOTALE: 1,80 KN/mq

Carichi Permanenti (qp)

-Pavimento in granito:
0,02m X 1,00m X 1,00m X 27KN/mq / 1,00mq= 0,54 KN/mq
-Massetto (calcestruzzi leggeri):
0,05m X 1,00m X 1,00m X 14,00KN/mc / 1,00 mq= 0,70 KN/mq
-Poliuretano espanso:
0,04m X 1,00m X 1,00m X 0,35KN/mc / 1,00mq= 0,01 KN/mq
-Pignatte:
0,16m X 0,40m X 1,00m X 5,00 KN/mc X2 (numero di pignatte in un metro lineare) / 1,00mq =0,64 KN/mq
-Tramezzi:1,00 KN/mq
-Impianti: 0,50 KN/mq

TOTALE: 3,39 KN/mq

Carichi Accidentali (qa)

-2 KN/mq

Per calcolare le sigma (sig_fa e sig_ca), abbiamo dovuto inserire dei dati riguardanti le caratteristiche dei materiali:
-per l’acciaio necessitiamo la tensione caratteristica di snervamento (l’armatura deve resistere a trazione) fy. Scegliamo una classe B450A con un limite di snervamento di 450MPa e dividiamolo per il coefficiente parziale di sicurezza relativo all’acciaio (1.15).
-per il calcestruzzo invece abbiamo bisogno della resistenza caratteristica cilindrica a compressione del calcestruzzo a 28 giorni Rck (nel nostro caso C40/50) per moltiplicarla per un fattore di riduttivo per le resistenze a lunga durata  (0,85). Il risultato andrà diviso per il coefficiente parziale di sicurezza relativo al calcestruzzo (1,5).

Aggiungiamo l’ultimo dato delta, ovvero l’altezza del copriferrro.

Il foglio Excel ha calcolato un H necessaria di 41,24cm, scegliamo quindi un altezza di 45,00cm e verifichiamo.

qtrave= 0,30m X 0,45m X 1,00m X 25,00KN/mc / 4,00m (interasse, per trovare il peso al metro lineare)= 0,84Kn/mq

Sommiamo il peso ai carichi strutturali prima analizzati e verifichiamo.

Con la sezione scelta 30X45 la trave è verificata.

SOLAIO IN ACCIAIO

Carichi Strutturale (qs)

-Lamiera Grecata + Soletta CLS (A55/P600):
2,40KN/mq
-Travetto IPE160:
0,158KN/mq X 2(numero travetti in un metro lineare) = 0,316KN/mq

TOTALE: 2,558 KN/mq

Carichi Permanenti (qp)

-Pavimento in granito:
0,02m X 1,00m X 1,00m X 27KN/mq / 1,00mq= 0,54 KN/mq
-Massetto (calcestruzzi leggeri):
0,05m X 1,00m X 1,00m X 14,00KN/mc / 1,00 mq= 0,70 KN/mq
-Poliuretano espanso:
0,04m X 1,00m X 1,00m X 0,35KN/mc / 1,00mq= 0,01 KN/mq
-Tramezzi:1,00 KN/mq
-Impianti: 0,50 KN/mq

TOTALE: 2.75 KN/mq

Carichi Accidentali (qa)

-2 KN/mq

Possiamo ora calcolare il momento.
Per determinare la sigma abbiamo bisogno della resistenza caratteristica fy,k, che ovviamente varia a seconda della tipologia di acciaio scelto. Nel nostro caso classe Fe 430/S275 con una resistenza di 275 Mpa.
Dalla resistenza caratteristica calcolata Wx (745,23cmc) prendiamo uan trave IPE300 con resistenza 903,6cmc.

Verifichiamo aggiungendo il peso della trave stessa.

qtrave= 0,571KN/mq / 4,00m (interasse, per trovare il peso al metro lineare)= 0,143Kn/mq

Sommiamo il peso ai carichi strutturali prima analizzati e verifichiamo.

Con la sezione IPE300 la trave è verificata.

Analisi di una trave reticolare 2D

Andremo ora ad esplicare come procedere per l’analisi di una struttura reticolare BIDIMENSIONALE con il programma SAP.
Useremo questa prima parte del post come esercitazione, per poter poi riutilizzare i passaggi per l’analisi di una struttura in 3 dimensioni.

1)Una volta aperto il software, creiamo un nuovo modello utilizzando un template prestabilito; in questo caso 2D Trusses, che appunto ci permetterà di realizzare una trave reticolare standard cambiando alcuni parametri. Selezioniamo poi l’unità “KN,m,C”.

2)Selezioniamo sloped truss e andiamo a dimensionare la trave utilizzando i parametri disponibili: numero di suddivisioni, altezza (metri nel nostro caso), lunghezza aste orizzontali.

3)Apparirà ora la nostra trave, nelle due viste da me precedentemente stabilite. Notiamo come di default, il software imposta la struttura isostaticamente, disegnando una trave appoggiata-appoggiata su cerniera-carrello.

4)Selezioniamo tutte le aste, andiamo su Define/Section Properties/Frame Sections per scegliere sezione e materiale da applicare.

5)Aggiungiamo una nuova proprietà, Add New Property, selezioniamo Steel (acciaio) e, per mia scelta, utilizziamo la sezione Pipe.

6)Il software SAP, rileva di base, i nodi, come nodi rigidi. Dobbiamo quindi andare a rendere questi ultimi liberi di ruotare, impedendo la trasmissione di momento tra le aste, in modo tale da avere tale tensione pari a 0.
Una volta selezionate le aste andiamo su Assign/Frame/Releases-Partial Fixity.

7)Selezioniamo il Moment 33 (Major) sia su Start (Inizio asta) e End (Fine asta).

8)Sul prospetto della trave si vedrà ora la struttura con le aste libere di ruotare.

9)Applichiamo dei carichi puntuali selezionando i nodi, poi andando su Assign/Joint Loads/Forces.

10)Creiamo un nuovo pattern che non consideri il peso proprio della struttura; Self Weight Multiplier=0.

11)Inseriamo una forza verticale Force Global X= -100 KN, quindi verso il basso ma ricordiamo di inserirla nel nostro pattern e usare l’unità di misura da noi scelta inizialmente.

12)Nella vista 3D, vediamo ora le forze applicate.

13)Per calcolare la struttura selezioniamo Run e scegliamo i carichi da analizzare, nel nostro caso, solo “NO SELF WEIGHT”.

14)Apparirà ora la struttura deformata nella vista 3D.

15)Andiamo su Show Forces-Stresses selezioniamo Joints per vedere le reazioni vincolari o Frames/Cambles/Tendons per le tensioni.  Chiediamo al software di graficizzare solo le tensioni assiali (dato che le altre sono uguali a 0). Tra le opzioni possiamo scegliere se graficizzarle  con Fill, ovvero colorate, dove in blu saranno rappresentati gli sforzi di trazione (tiranti) e in rosso gli sforzi di compressione (puntoni), oppure con Show Values on Diagram, dando i vari valori numerici delle tensioni.

16)Andando su Display/Show Tables e selezionando ANALYSIS RESULTS (sempre non tenendo conto del peso proprio della struttura), il software elaborerà una tabella con i vari valori di tensioni, esportabile su Excell (File/Export to Excell).

17)Dalla tabella notiamo come P, V2, V3, T, M2 e M3 (rispettivamente i tagli nei due diversi piani, la torsione e i momenti sui due diversi piani) siano uguali a 0, mentre P, lo sforzo normale, avrà dei valori diversi da zero. Selezionando Ordina e Filtra, possiamo ordinare le file tenendo in considerazione la colonna P in ordine decrescente, in modo tale da sapere quali sono le aste soggette a più alta tensione. Le aste sono classificate numericamente. Per conoscere i rispettivi nomi delle aste, torniamo sul software, selezioniamo Set display options e abilitiamo la visualizzazione dei Labels su Frames-Cables-Tendons.

Analisi di una copertura reticolare 3D importata dal software Rhinoceros

A)Il software SAP, da la possibilità di disegnare manualmente una struttura. Questa applicazione però non è semplice come per altri software specificatamente creati per il disegno CAD.
Ho disegnato quindi la struttura con Rhinoceros salvando il file .IGES, Initial Graphics Exchange Specification, formato creato per lo scambio di file CAD neutro, senza superfici, quindi, wireframe.

B)SAP riconoscerà i segmenti come singole aste, di conseguenza non deve essere usata la polilinea nel software di disegno.

C)Una volta importata la copertura, come nel caso 2D dobbiamo inserire le cerniere interne, perché ricordiamo, SAP riconosce i nodi generati dall’incontro di due segmenti, come nodi rigidi.
Questa volta selezioneremo sia Moment 22 che Moment 33, per permettere la rotazione in tutte le direzioni.

D)Cambiamo la vista della pianta abbassandola a Z=0 in modo tale da poter inserire i vincoli cerniera negli 8 punti di appoggio da me selezionati in modo più semplice.

E)Selezioniamo tutte le aste e come specificato nel punto 5 per il 2D andando su Define/Section Properties/Frame Sections, creiamo un materiale chiamato TUBOLARE, utilizzando una sezione appunto rotonda. Andando Set display options possiamo selezionare Sections, su Frames-Cables-Tendons per visualizzare il material di ogni singola asta.

F)Selezioniamo tutti i nodi su cui vogliamo applicare una forza e riferendoci al punto 10, ricordandoci di usare il Pattern NO SELF WEIGHT.

G)Dato che abbiamo importato un file da un programma esterno, andiamo a fare un check dei nodi, applicando una tolleranza minima di default.  Andiamo quindi su Edit/Edit Points/Merge Joints.

H)Andiamo su Run, facendo riferimento al punto 14, apparirà quindi la deformata sulla vista 3D.

I) Come detto nel punto 16, andiamo su Show Forces-Stresses e chiediamo al software di graficizzare prima le reazioni vincolari poi solo le tensioni assiali nei due metodi prima analizzati (Fill e Show Values on Diagram)

L)Esportiamo la tabella excell e ordiniamo le file in ordine decrescente tenendo conto dello sforzo normale (P). Notiamo come anche in questo caso Tagli, Momenti e Torsione sono uguali a 0.