EXE4_Studio del Centro delle Rigidezze di una struttura a telaio di tipo Shear-Type e verifica su Sap.

EXE4_Studio del Centro delle Rigidezze di una struttura a telaio di tipo Shear-Type e verifica su Sap.

Con quest’esercitazione vogliamo studiare il comportamento di un impalcato quando esso è sollecitato da forze esterne di tipo orizzontale e di come i suoi controventi, progettati per questa struttura, rispondano a quest’ultime. La rappresentazione grafica, «l’avatar» dei controventi si configura come una molla, tesa alla più immediata fruizione del comportamento dei controventi, elastico reversibile. L’obiettivo, una volta calcolata la rigidezza delle molle, è quello di calcolare il centro di tutte le rigidezze dei controventi, luogo dei punti in cui le forze esterne applicate avranno un momento pari a zero, con conseguente rotazione rigida nulla di tutto l’impalcato.

Dunque, una volta effettuato il dimensionamento e la scelta della tipologia costruttiva (in questo caso abbiamo preferito una tecnologia in c.l.s. armato), attraverso uno strumento di calcolo elettronico, un foglio excel, riusciremo ad inserire tutti i dati e ad ottenere i risultati cercati: CALCOLO DEL CENTRO DELLE RIGIDEZZE.

Pianta dell’impalcato in c.l.s. armato - Sezione impalcato.

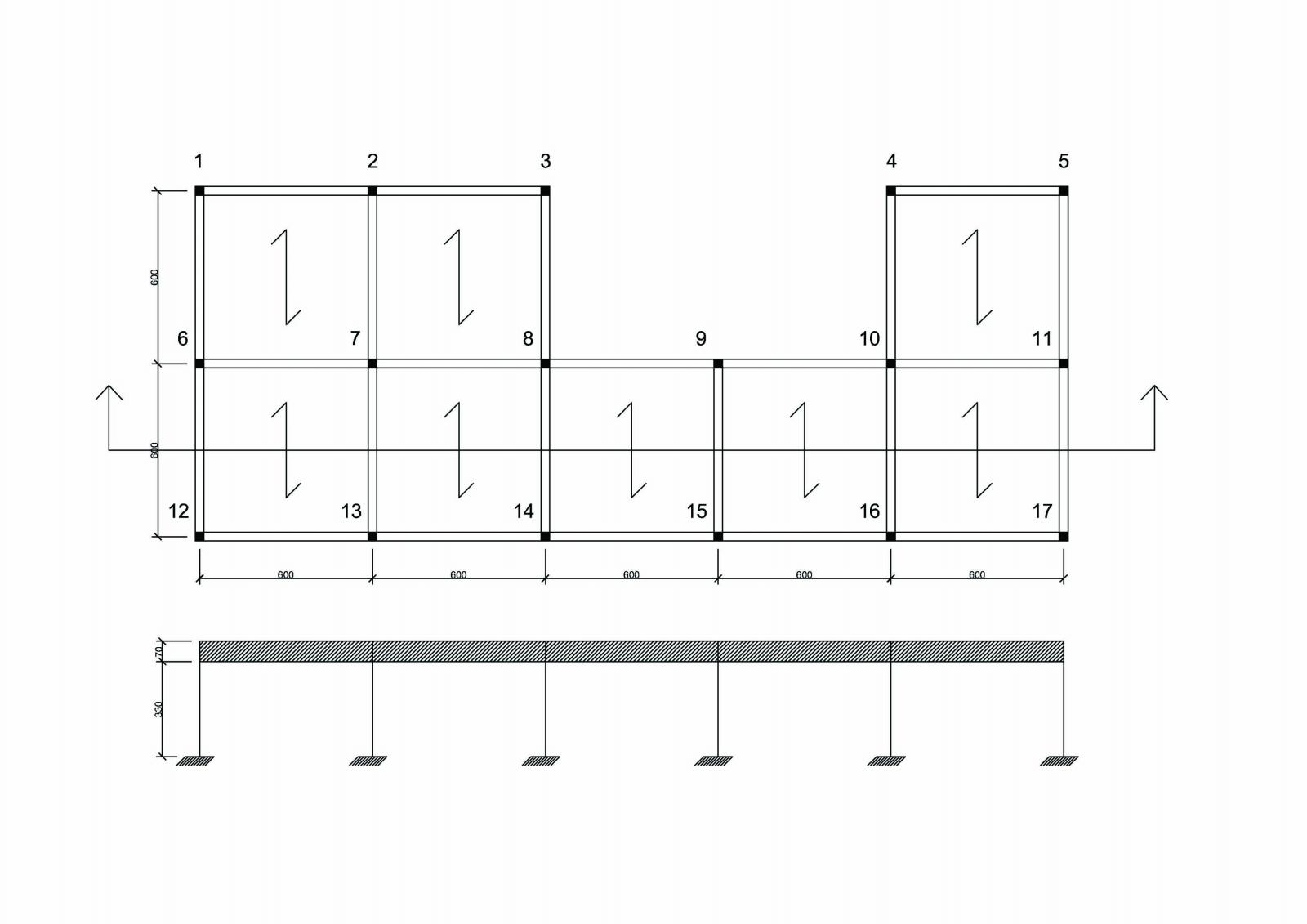
Rappresentazione «avatar» delle rigidezze K dell’impalcato in esame:

Definiamo un sistema di riferimento cartesiano, assi X-Y, e calcoliamo la distanza di ogni singolo controvento dall’origine degli assi, siano essi disposti in senso verticale (dv) sia in senso orizzontale (do):

dv1: 0 cm

dv2: 6 cm

dv3: 12 cm

dv4: 18 cm

dv5: 24 cm

dv6: 30 cm

do1: 0 cm

do2: 6 cm

do3: 12 cm

Sezione dei pilastri = 30x30 cm

Altezza dei pilastri in c.l.s. armato: H = 400 cm

Modulo di Young (E) = 21000 N/mm

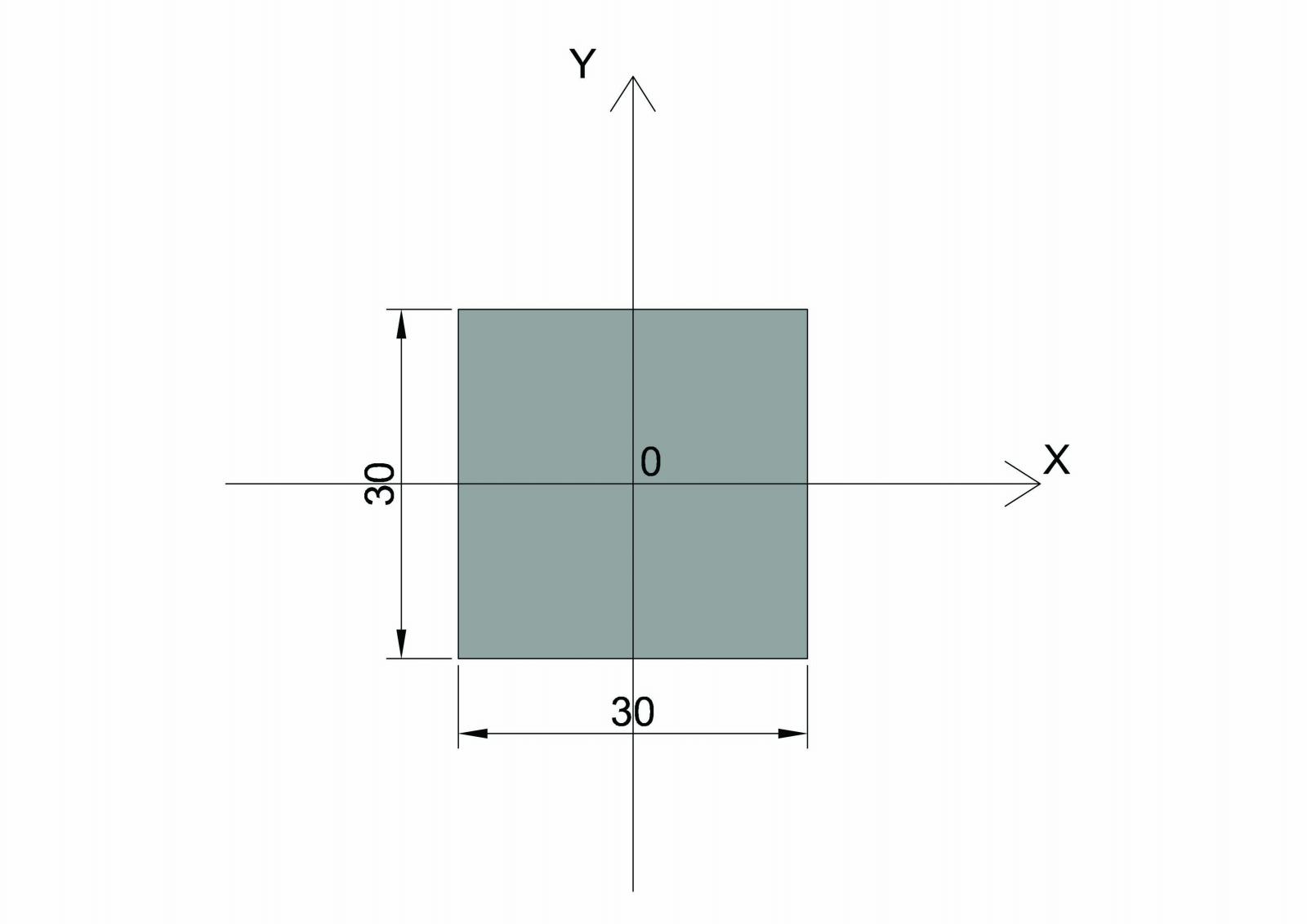
È importante, a questo punto, nominare numericamente ogni pilastro così da poter definire ogni telaio, rispetto al numero dei pilastri che lo compongono sia nella direzione x che nella direzione y:

Telaio:                    n° pilastri:

    1                          1-6-12

    2                          2-7-13

    3                          3-8-14

    4                            9-15

    5                         4-10-16

    6                         5-11-17

    7                       1-2-3-4-5

    8                    6-7-8-9-10-11

    9                12-13-14-15-16-17

Iniziamo ora a compilare la tabella excel:

• STEP1: calcolo delle rigidezze traslanti dei controventi dell'edificio: data dalla somma delle rigidezze di ciascun pilastro che compone ciascun telaio.

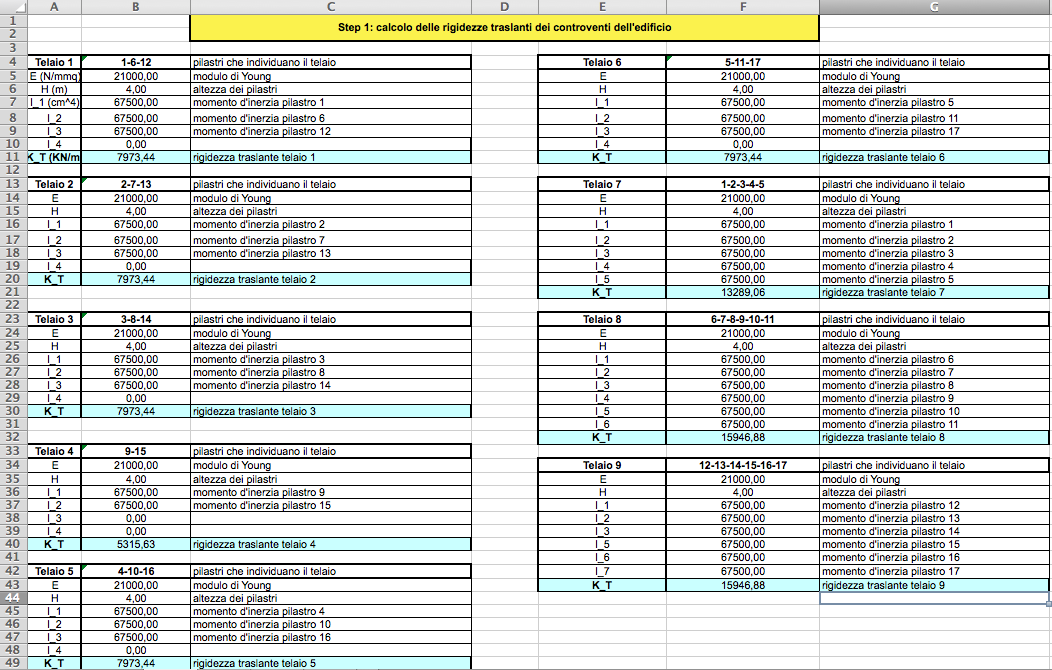
• STEP2: Tabella sinottica dei controventi e delle loro distanze dell’origine
:

• STEP3: CALCOLO DEL CENTRO DI MASSA: dopo aver suddiviso la pianta dell’impalcato in macro aree, geometricamente riconducibili a figure semplici, come rettangoli o quadrati, si procede alla determinazione del baricentro:

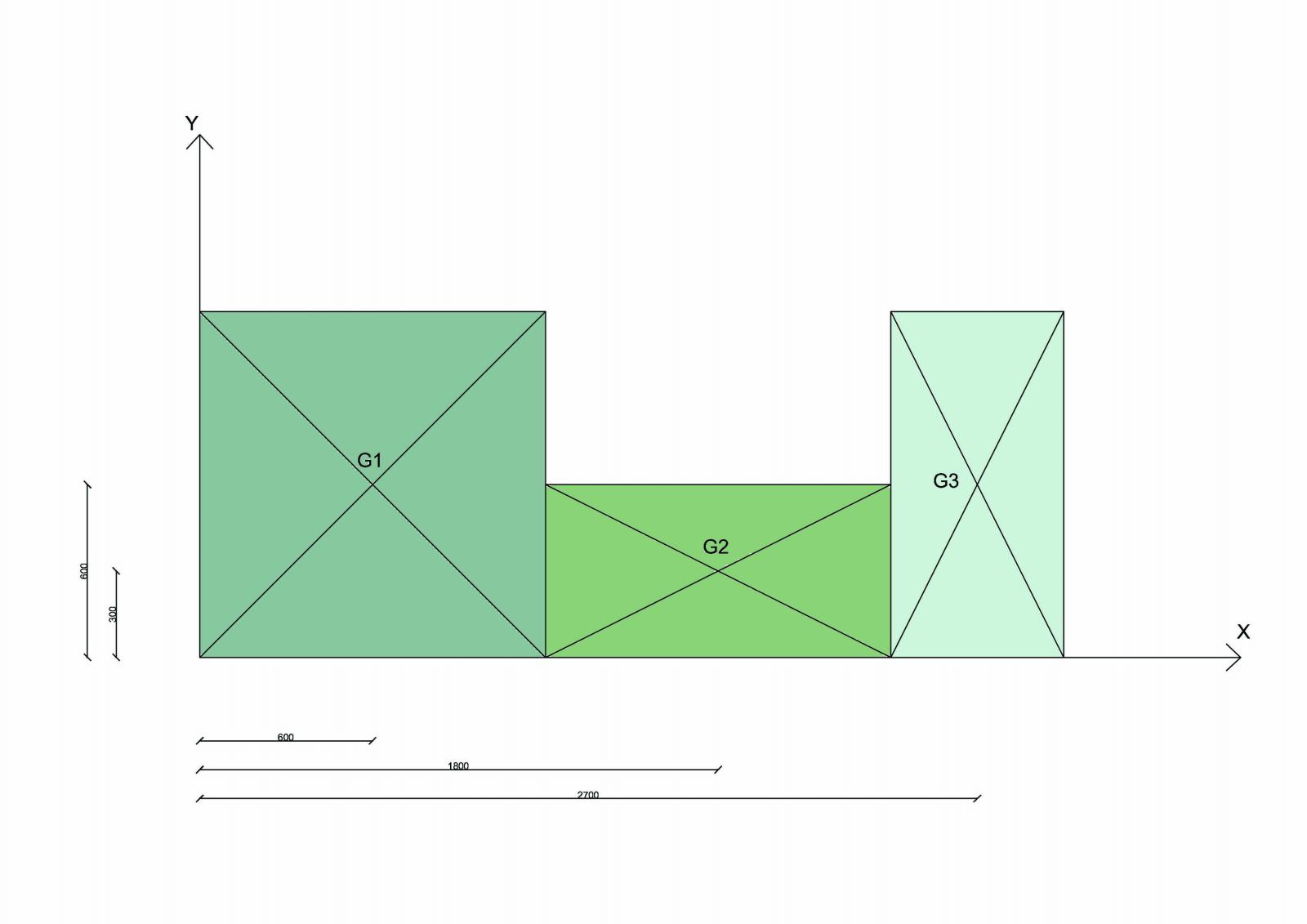
• STEP4: calcolo del centro di rigidezze e delle rigidezze globali: sommo tutte le rigidezze dei controventi, prima nella direzione orizzontale e poi in quella verticale. A questo punto posso determinare il centro delle rigidezze, rispetto alla sua coordinata x e y, facendo il rapporto tra la sommatoria del prodotto, di ogni singola rigidezza per il proprio braccio, per la rigidezza totale, sia verticale sia orizzontale. Il passo successivo sarà quello di calcolare la rigidezza torsionale (K): la sommatoria dei prodotti delle rigidezze di ciascun telaio per la distanza al quadrato di ognuno di essi rispetto a C = (x,y).

• STEP5: ANALISI DEI CARICHI SISMICI: Individuo il carico Q del solaio (somma di qs+qp+qa) e lo moltiplico per il coefficiente di contemporaneità (y), ottenendo così i pesi sismici. Successivamente moltiplico tale valore per il coefficiente d’intensità sismica (c), ottenendo così il valore della forza sismica orizzontale.

• STEP6/7: Ripartizione della forza sismica lungo X e Y: adesso posso capire come la forza sismica potrebbe ripartirsi lungo le due direzioni dell’impalcato. Il foglio excel, così concepito, mi permette di trovare direttamente la traslazione orizzontale e quella verticale e conseguentemente la rotazione dell’impalcato. È ora possibile, dunque, individuare come ogni forza sismica si ripartisce per ciascun telaio, ricavandone infine le reazioni di contrasto che ogni impalcato esercita al fine di contrastare la suddetta forza sismica orizzontale. 

Per avere una successiva verifica dei calcoli appena studiati, possiamo ora disegnare su Sap2000 la struttura dell’impalcato analizzata, così da verificarne la corrispondenza dei valori e visualizzare la deformazione messa in atto dall’azione del sisma orizzontale. 

• Importiamo il modello dell’impalcato, disegnato su rhinoceros, in ambiente Sap2000, ricordandosi di prestare attenzione alla coerenza delle unità di misura. 

• Assegniamo i vincoli esterni di tipo incastro alla base di ogni pilastro. 

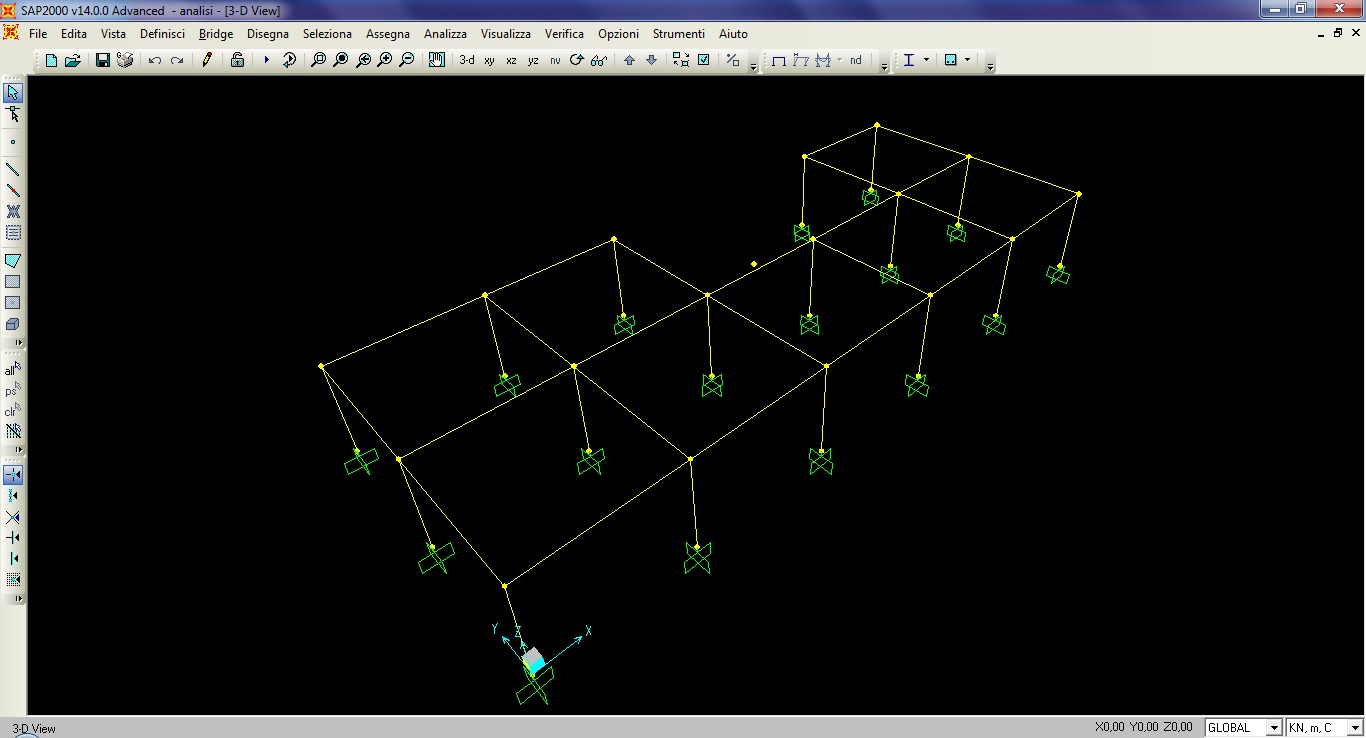
• Assegnami ai pilastri una sezione in cemento armato 0,3 x 0,3 m. 

• Assegniamo alle travi una sezione in cemento armato 0,3 x 0,7 m. Modifichiamo le proprietà della sezione della trave con l’obiettivo di renderla infinitamente rigida, tipicamente Shear-Type. A tal fine aumentiamo spropositatamente i valori del momento d’inerzia in asse 2 (y) e 3 (x).  

• Definiamo l’impalcato rigido del “solaio”: selezioniamo tutti i nodi dell’impalcato, compreso il centro delle rigidezze. Assegna --> nodi --> vincoli interni --> tipo di vincolo --> Diaphragm, che conferisce all’intera aria selezionata rigidezza tale da non avere dilatazioni né accorciamenti, ma solo traslazioni. 

• Definiamo lo schema di carico della forza sismica orizzontale: Definisci --> schemi di carico --> agg. Nuovo schema carico --> peso proprio moltiplicat. = 0 --> OK.

• Selezioniamo il centro delle rigidezze e assegniamoli lo schema di carico appena definito nella direzione y, con valore 230,40 KN.

• Lanciamo l’analisi e verifichiamone gli spostamenti. 

• Con essa prendiamo coscienza del fatto che l’unico spostamento rigido di cui tener conto è quello in asse y, nella direzione della forza sismica orizzontale. La rotazione rigida risulta quasi nulla e, perciò, trascurabile. 

Featuring Tommaso Ruetta.

                                                                                - fine - 

                                                                                   A.P.