blog di alessandro.petroni

EXE5_MODELLAZIONE GEOMETRICA DELL’ARCO E SUA ANALISI SU SAP2000.

Con quest’esercitazione si prendono in esame tre differenti tipologie di arco:

• Arco a tutto sesto, con altezza (h) = 300 cm
• Arco ribassato, con altezza (h) = 150 cm
• Arco parabolico, con altezza (h) = 400 cm

Ipotizzando che tutte e tre le strutture abbiano una sezione di 30x40cm in calcestruzzo armato, una luce (L) pari a 600cm; tutte ugualmente soggette a un carico uniformemente distribuito pari a 10 KN/m; possiamo metterle su Sap2000 e analizzarne il comportamento:

Prima di andare sul programma, disegniamo i tre diversi tipi di arco su AutoCAD, avendo cura di spezzare ognuno di essi in chiave e di non disegnare con il layer 0. 

 

Elenco i passaggi chiave per l’analisi con Sap2000:

Step1: Dopo aver salvato il file in Dxf2004 importiamolo su Sap2000 prestando molta attenzione alle unità di misura.

 

Step2: Assegniamo il vincolo esterno della cerniera alle due sezioni d’imposta dell’arco: selezionare punti in imposta --> Assegna --> Nodo --> Vincoli Esterni --> Cerniera.

 

Step3: Assegniamo il vincolo interno della cerniera al punto in chiave dell’arco, selezionandone le due aste più vicine e rilasciandone i momenti 33 in entrambe le direzioni: Assegna --> Frame --> Rilasci/SemiIcastri --> spuntare rilasci, sia inizio che fine, del momento 33 (maggiore).

 

Step4: Assegniamo un materiale e una sezione alla struttura: selezioniamo tutto l’arco --> Assegna --> Frame --> Sezioni Frame --> Agg. Nuova Proprietà --> Concrete --> Nome sezione --> inseriamo Altezza (0.30) e Larghezza ( 0.40) --> ok.

 

Step5: Carichiamo la struttura con un carico distribuito pari a 10 KN/m: selezioniamo tutto l’arco --> Assegna --> Carichi Frame --> Distribuito --> + --> inseriamo un nome al nuovo carico e azzeriamone il peso proprio --> Agg. Nuovo Schema Carico --> Direzione Gravity Projected --> e inseriamo il valore di carico uniforme pari a 10.

Step6: Avviamo l’analisi e studiamo i diagrammi ottenuti.

 

Ripetendo questi semplici passaggi per ogni struttura, ad arco, progettata, possiamo, in seguito, procedere con il confronto dei diagrammi e le conclusioni. 

 

ARCO A TUTTO SESTO:

• Deformata

• Reazioni vincolari

• F. Assiale 

• Taglio

• Momento

 

ARCO RIBASSATO:

 

• Deformata

• Reazioni vincolari

• F. Assiale 

• Taglio

• Momento

 

ARCO PARABOLICO:

 

• Deformata

• Reazioni vincolari

• F. Assiale 

 

Concludendo, possiamo affermare che la geometria dell’arco, in termini strutturali, tanto più è ribassata tanto più è spingente, cioè tanto più la sua altezza è minore della metà della sua luce (campata) tanto più è “arco”!!!

         

                                                                                         - fine -

                                                                                             A.

 

 

 

 

EXE3_VERIFICA ABBASSAMENTO TRAVE A SBALZO:

Con riferimento alla pianta strutturale (sopra disegnata) di un solaio nel quale sono presenti delle travi a sbalzo e ipotizzandone tre tecnologie, siano esse: legno – acciaio – c.l.s. armato, verifichiamo, con quest’esercitazione, l’abbassamento della trave predisposta al sostenimento di tale sbalzo, in riferimento al rapporto di verifica che ci dice: abbassamento < luce_sbalzo/250.  

Consideriamo un interasse di 500 cm e una luce di 300 cm.

Con riferimento alle tecnologie scelte per l’EXE2, in precedenza postata, consideriamo che nel caso di trave incastrata, da un lato, e con un estremo libero, dall’altro (la così detta mensola), il momento flettente M è pari a ql²/2.

 

 

Tipologia di LEGNO: 

Utilizzo un tipo di legno lamellare con un modulo di resistenza a flessione (f_m,k) pari a 24 N/mm², e un modulo di elasticità (E) pari a 8000 N/mm², avremo: 

Il dimensionamento risulta corretto e il rapporto: abbassamento < luce_sbalzo/250 è verificato.

 

Tipologia di ACCIAIO: 

Utilizzo un valore pari a 275 N/mm² per la tensione/resistenza caratteristica di snervamento dell’acciaio (f_y,k), e  un modulo di elasticità (E) pari a 210000 N/mm², avremo:

Alla fine scegliamo una IPE400, della quale consideriamo:

Peso = 66,3 Kg/m

Momento d’inerzia (Jx) = 23130,0 cm⁴

 

Il dimensionamento risulta corretto e il rapporto: abbassamento < luce_sbalzo/250 è verificato.

 

Tipologia di C.L.S armato: 

Utilizzo modulo di resistenza a flessione (f_c,k) pari a 40 N/mm² ,della classe di resistenza del calcestruzzo ordinario C32/40, e un modulo di elasticità (E) pari a 21000 N/mm², avremo: 

Il dimensionamento risulta corretto e il rapporto abbassamento < luce_sbalzo/250 è verificato.

 

 

                                                                           - fine -

                                                                               A.

 

 

 

 

 

 

 

EXE4_Studio del Centro delle Rigidezze di una struttura a telaio di tipo Shear-Type e verifica su Sap.

 

Con quest’esercitazione vogliamo studiare il comportamento di un impalcato quando esso è sollecitato da forze esterne di tipo orizzontale e di come i suoi controventi, progettati per questa struttura, rispondano a quest’ultime. La rappresentazione grafica, «l’avatar» dei controventi si configura come una molla, tesa alla più immediata fruizione del comportamento dei controventi, elastico reversibile. L’obiettivo, una volta calcolata la rigidezza delle molle, è quello di calcolare il centro di tutte le rigidezze dei controventi, luogo dei punti in cui le forze esterne applicate avranno un momento pari a zero, con conseguente rotazione rigida nulla di tutto l’impalcato.

Dunque, una volta effettuato il dimensionamento e la scelta della tipologia costruttiva (in questo caso abbiamo preferito una tecnologia in c.l.s. armato), attraverso uno strumento di calcolo elettronico, un foglio excel, riusciremo ad inserire tutti i dati e ad ottenere i risultati cercati: CALCOLO DEL CENTRO DELLE RIGIDEZZE.

Pianta dell’impalcato in c.l.s. armato - Sezione impalcato.

Rappresentazione «avatar» delle rigidezze K dell’impalcato in esame:

Definiamo un sistema di riferimento cartesiano, assi X-Y, e calcoliamo la distanza di ogni singolo controvento dall’origine degli assi, siano essi disposti in senso verticale (dv) sia in senso orizzontale (do):

dv1: 0 cm

dv2: 6 cm

dv3: 12 cm

dv4: 18 cm

dv5: 24 cm

dv6: 30 cm

do1: 0 cm

do2: 6 cm

do3: 12 cm

Sezione dei pilastri = 30x30 cm

Altezza dei pilastri in c.l.s. armato: H = 400 cm

Modulo di Young (E) = 21000 N/mm

È importante, a questo punto, nominare numericamente ogni pilastro così da poter definire ogni telaio, rispetto al numero dei pilastri che lo compongono sia nella direzione x che nella direzione y:

Telaio:                    n° pilastri:

    1                          1-6-12

    2                          2-7-13

    3                          3-8-14

    4                            9-15

    5                         4-10-16

    6                         5-11-17

    7                       1-2-3-4-5

    8                    6-7-8-9-10-11

    9                12-13-14-15-16-17

 

Iniziamo ora a compilare la tabella excel:

 

• STEP1: calcolo delle rigidezze traslanti dei controventi dell'edificio: data dalla somma delle rigidezze di ciascun pilastro che compone ciascun telaio.

• STEP2: Tabella sinottica dei controventi e delle loro distanze dell’origine
:

• STEP3: CALCOLO DEL CENTRO DI MASSA: dopo aver suddiviso la pianta dell’impalcato in macro aree, geometricamente riconducibili a figure semplici, come rettangoli o quadrati, si procede alla determinazione del baricentro:

• STEP4: calcolo del centro di rigidezze e delle rigidezze globali: sommo tutte le rigidezze dei controventi, prima nella direzione orizzontale e poi in quella verticale. A questo punto posso determinare il centro delle rigidezze, rispetto alla sua coordinata x e y, facendo il rapporto tra la sommatoria del prodotto, di ogni singola rigidezza per il proprio braccio, per la rigidezza totale, sia verticale sia orizzontale. Il passo successivo sarà quello di calcolare la rigidezza torsionale (K): la sommatoria dei prodotti delle rigidezze di ciascun telaio per la distanza al quadrato di ognuno di essi rispetto a C = (x,y).

• STEP5: ANALISI DEI CARICHI SISMICI: Individuo il carico Q del solaio (somma di qs+qp+qa) e lo moltiplico per il coefficiente di contemporaneità (y), ottenendo così i pesi sismici. Successivamente moltiplico tale valore per il coefficiente d’intensità sismica (c), ottenendo così il valore della forza sismica orizzontale.

• STEP6/7: Ripartizione della forza sismica lungo X e Y: adesso posso capire come la forza sismica potrebbe ripartirsi lungo le due direzioni dell’impalcato. Il foglio excel, così concepito, mi permette di trovare direttamente la traslazione orizzontale e quella verticale e conseguentemente la rotazione dell’impalcato. È ora possibile, dunque, individuare come ogni forza sismica si ripartisce per ciascun telaio, ricavandone infine le reazioni di contrasto che ogni impalcato esercita al fine di contrastare la suddetta forza sismica orizzontale. 

 

Per avere una successiva verifica dei calcoli appena studiati, possiamo ora disegnare su Sap2000 la struttura dell’impalcato analizzata, così da verificarne la corrispondenza dei valori e visualizzare la deformazione messa in atto dall’azione del sisma orizzontale. 

• Importiamo il modello dell’impalcato, disegnato su rhinoceros, in ambiente Sap2000, ricordandosi di prestare attenzione alla coerenza delle unità di misura. 

• Assegniamo i vincoli esterni di tipo incastro alla base di ogni pilastro. 

• Assegnami ai pilastri una sezione in cemento armato 0,3 x 0,3 m. 

• Assegniamo alle travi una sezione in cemento armato 0,3 x 0,7 m. Modifichiamo le proprietà della sezione della trave con l’obiettivo di renderla infinitamente rigida, tipicamente Shear-Type. A tal fine aumentiamo spropositatamente i valori del momento d’inerzia in asse 2 (y) e 3 (x).  

• Definiamo l’impalcato rigido del “solaio”: selezioniamo tutti i nodi dell’impalcato, compreso il centro delle rigidezze. Assegna --> nodi --> vincoli interni --> tipo di vincolo --> Diaphragm, che conferisce all’intera aria selezionata rigidezza tale da non avere dilatazioni né accorciamenti, ma solo traslazioni. 

• Definiamo lo schema di carico della forza sismica orizzontale: Definisci --> schemi di carico --> agg. Nuovo schema carico --> peso proprio moltiplicat. = 0 --> OK.

• Selezioniamo il centro delle rigidezze e assegniamoli lo schema di carico appena definito nella direzione y, con valore 230,40 KN.

• Lanciamo l’analisi e verifichiamone gli spostamenti. 

• Con essa prendiamo coscienza del fatto che l’unico spostamento rigido di cui tener conto è quello in asse y, nella direzione della forza sismica orizzontale. La rotazione rigida risulta quasi nulla e, perciò, trascurabile. 

Featuring Tommaso Ruetta.

                                                                                - fine - 

                                                                                   A.P.

 

Prendiamo in esame la trave più sollecitata nella seguente struttura a telaio, nelle tre tipologie tecnologiche del legno, acciaio e cls armato, e portiamone a termine il dimensionamento.

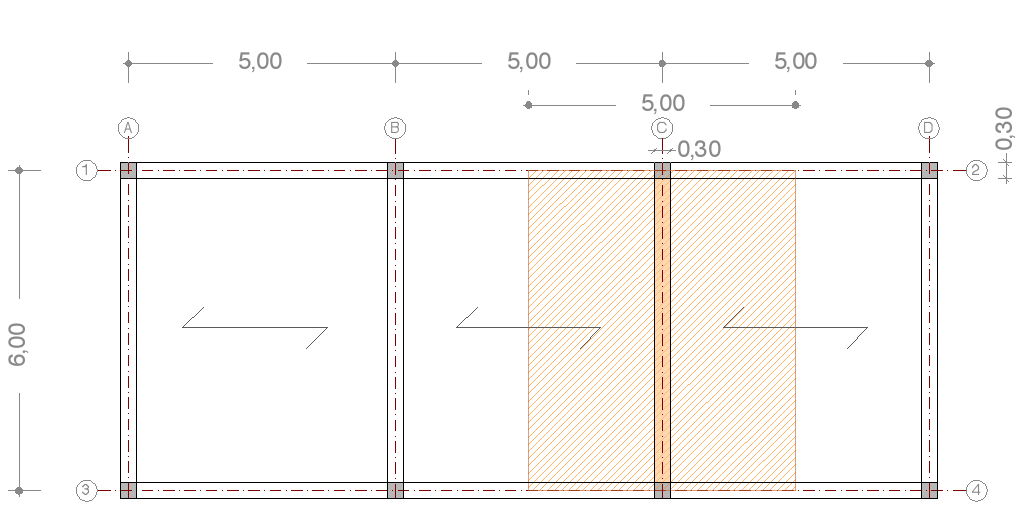
Consideriamo la trave nell’area di pertinenza maggiore (nella pianta del solaio evidenziata dal color arancio), che in questa struttura occupa 30m², con un interasse tra le travi di 5m e una luce di 6m.

Premettendo che per il dimensionamento della trave si rende essenziale analizzarne i carichi che su di essa gravano, essi si possono classificare in tre macro categorie:

• Carichi strutturali (Qs), corrispondenti al peso delle parti strutturali del solaio, escludendone la trave principale, essendo essa l’incognita del problema.

• Carichi permanenti (Qp), corrispondenti al peso delle parti non strutturali del solaio, compreso il peso dei tramezzi e degli impianti standardizzati dalla normativa.

• Carichi accidentali (Qa), corrispondenti alla destinazione d’uso della suddetta architettura ed eventualmente tenendo conto degli agenti atmosferici che su di essa, considerato il sito di progetto, potrebbero gravare.

 

SOLAIO IN LEGNO

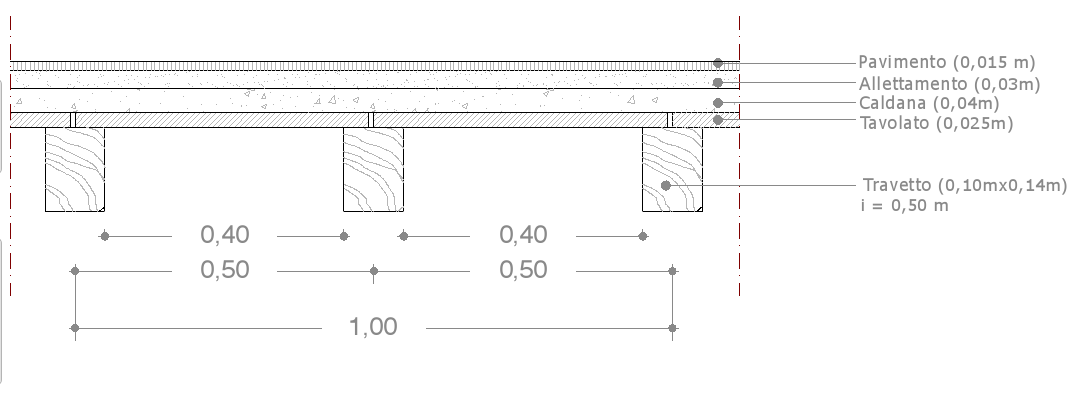
  Composizione della sezione              Peso specifico materiale

Qs

Tavolato in legno di pioppo =                     5,0 KN/m³

Travetti in legno di pioppo =                     5,0 KN/m³

 

Tavolato:

(0,025m x 1,00m x 1,00m)= 0,025m³ x 5,0KN/m³= 0,125KN/1m² = 0,125KN/m²

Travetti:

2 x (0,10m x 0,14m x 1m)= 0,028m³ x 5,0KN/m³= 0,14KN/1m² = 0,14KN/m²

 

Qs: 0,125KN/m² + 0,14KN/m² =0,265 KN/m²

 

Qp

 

Pavimento:

(0,015m x 1,00m x 1,00m)= 0,015m³ x 5,0KN/m³= 0,075KN/1m² = 0,075KN/m²

Allettamento:

(0,03m x 1,00m x 1,00m)= 0,03m³ x 21,0KN/m³= 0,63KN/1m² = 0,63KN/m²

Caldana:

(0,04m x 1,00m x 1,00m)= 0,04m³ x 24,0KN/m³= 0,96KN/1m² = 0,96KN/m²

Tramezzi:1KN/m²

Impianti:0,5KN/m²

 

Qp: 0,075KN/m² + 0,63KN/m² + 0,96KN/m² + 1,00KN/m² + 0,50KN/m² =3,165 KN/m²

 

Qa

Cat. A, Ambienti ad uso residenziale =             2,00 KN/m²

 

Considerato un interasse, pari a 5m, una luce, pari a 6m e una dimensione della base della trave, pari a 0,30m, possiamo ora compilare la tabella Excel, preventivamente programmata, inserendo tutti i valori trovati.

Con una base da 0,30m, i calcoli effettuati tramite la tabella Excel verificano il dimensionamento dell’altezza della trave a patire da una misura superiore ai 50,35cm. Dunque, per approssimazione, possiamo progettare una sezione da 30cm x 55cm. 

 

SOLAIO IN ACCIAIO

 

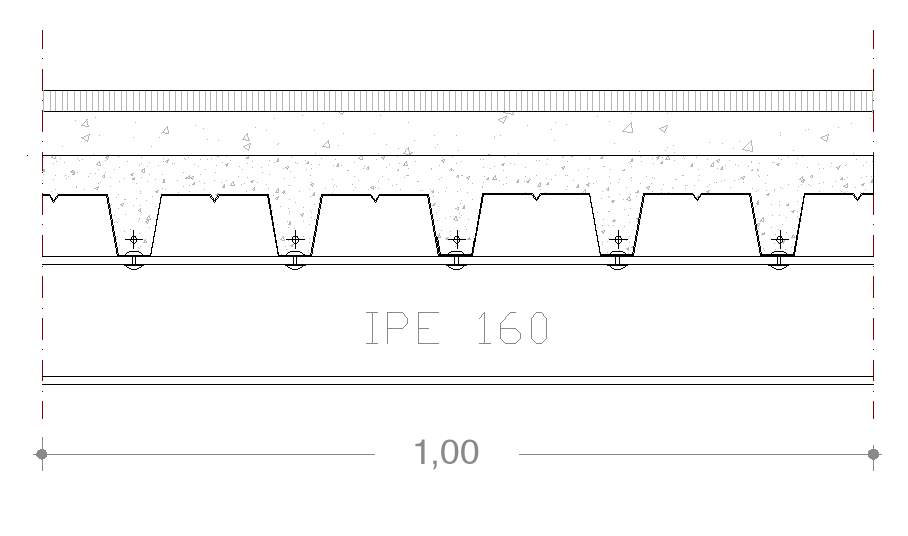
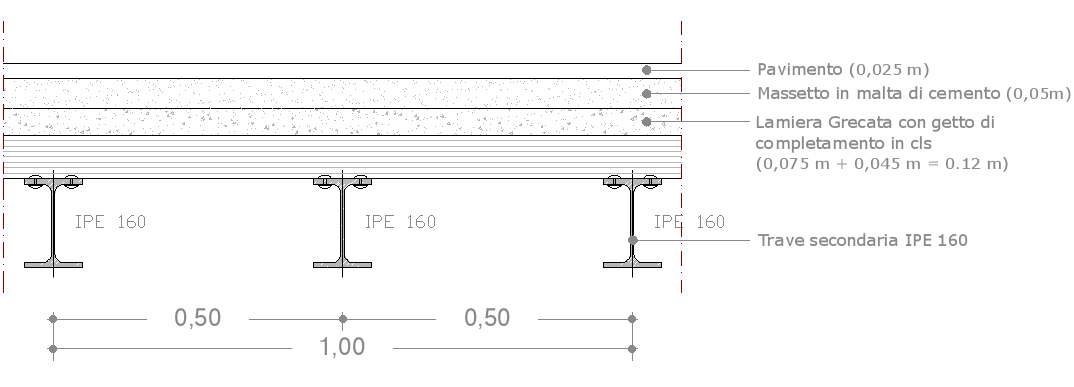
Composizione della sezione              Peso specifico materiale

Qs

 

IPE 160:

(0,0201m²x 1,00m) x 78,5KN/m³ = 1,58KN/1m² = 1,58KN/m²

Getto di calcestruzzo:

(0,0645m²x 1m)= 0,0645m³ x 24,0KN/m³= 1,548KN/1m² = 1,548KN/m²

 

Qs: 0,165KN/m² + 1,548KN/m² + 1,58KN/m² =3,293 KN/m²

 

Qp

Pavimento:

(0,025m x 1,00m x 1,00m)= 0,025m³ x 18,0KN/m³= 0,45KN/1m² = 0,45KN/m²

Massetto:

(0,05m x 1,00m x 1,00m)= 0,05m³ x 21,0KN/m³= 1,05KN/1m² = 1,05KN/m²

Tramezzi:1KN/m²

Impianti:0,5KN/m²

 

Qp: 0,45KN/m² + 1,05KN/m² + 1KN/m² + 0,5KN/m² =3 KN/m²

 

Qa

 

Considerato un interasse, pari a 5m, una luce, pari a 6m e una Tensione di snervamento caratteristica, pari a 275MPa, possiamo ora compilare la tabella Excel, preventivamente programmata, inserendo tutti i valori trovati.

Il calcolo restituisce un valore (Wx), modulo di resistenza a flessione, pari a 1052,02cm³. Approssimando tale valore, scelgo di utilizzare una trave con un Wx maggiore: IPE300 (Wx = 1318,00cm³).

 

 

SOLAIO IN C.A.

 

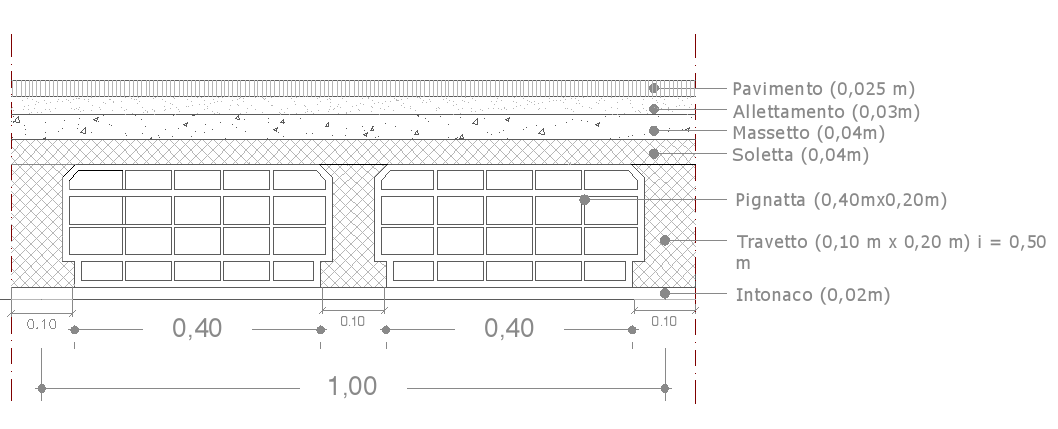
 Composizione della sezione              Peso specifico materiale

 

Qs

 

Travetto in calcestruzzo armato:

2 x (0,10m x 0,20m x 1,00m)= 0,04m³ x 25,0KN/m³= 1KN/1m² = 1KN/m²

Soletta in calcestruzzo armato:

(0,04m x 1m x 1m)= 0,04m³ x 25,0KN/m³= 1KN/1m² = 1KN/m²

 

Qs: 1KN/m² + 1KN/m² + 0,712KN/m² =2,712 KN/m²

 

Qp

 

Pavimento:

(0,025m x 1,00m x 1,00m)= 0,025m³ x 18,0KN/m³= 0,45KN/1m² = 0,45KN/m²

Allettamento:

(0,03m x 1,00m x 1,00m)= 0,03m³ x 18,0KN/m³= 0,54KN/1m² = 0,54KN/m²

Massetto:

(0,04m x 1,00m x 1,00m)= 0,04m³ x 21,0KN/m³= 0,84KN/1m² = 0,84KN/m²

intonaco:

(0,02m x 1,00m x 1,00m)= 0,02m³ x 18,0KN/m³= 0,36KN/1m² = 0,36KN/m²

Tramezzi:1KN/m²

Impianti:0,5KN/m²

 

Qp: 0,45KN/m² + 0,54KN/m² + 0,84KN/m² + 0,36KN/m² + 1KN/m² + 0,5KN/m² =3,69 KN/m²

 

Qa

 

Considerato un interasse, pari a 5m, una luce, pari a 6m, una base di 0,30m, una classe di resistenza dell’acciaio da armatura, pari a 450 MPa, e una classe di resistenza del calcestruzzo (Rck), pari a 30, possiamo ora compilare la tabella Excel, preventivamente programmata, inserendo tutti i valori trovati.

Il calcolo restituisce un’altezza totale (H) pari a 42,32cm. Approssimando tale valore, scelgo di utilizzare una trave con una sezione di:  30cm x 50cm

Posso verificare tale approssimazione sommando al Qs totale la qs della trave principale ipotizzata:

• (0,30m x 0,423m = 0,127m²), moltiplicarla per il peso specifico del calcestruzzo armato (0,127 m² x 25,0KN/m³= 3,17 KN/m) / 1m lineare = 3,17KN/m².

• Il risultato trovato va sommato al Qs totale e inserito nella tabella Excel per ripercorrere il percorso di calcolo precedentemente effettuato, infine controllare che l’altezza approssimata verifichi i dati ottenuti.

 

- fine - 

A.P.

 

 

 

 

 

Per lo studio e la progettazione di una trave reticolare tridimensionale ho pensato di ipotizzare l’esigenza di costruire una trave a sostegno di un solaio tipo per un edificio di abitazioni. Definito un modulo regolare standard, ipotetico, di 1x1x1 metri e ipotizzato che il carico che insiste per ogni metro quadrato potesse essere ricondotto a un valore generico di 20 KN, ho pensato che le aste si collegassero tra di loro, attraverso delle cerniere interne, a formare moduli di piramidi rovesciate. Tale struttura si caratterizza, pertanto, dalla presenza di elementi tesi, detti tiranti, ed elementi compressi, detti puntoni. 

• Modellare una trave reticolare nelle tre dimensioni direttamente su SAP2000 non è semplice! Questo, però, può essere propedeutico all’apprendimento di questo programma. Perciò, ho deciso di usare solamente SAP per l’interno studio della trave: dalla progettazione allo studio strutturale. Fondamentale è ricordarsi d’impostare immediatamente le unità di misura che corrispondono a: KN, m, C. Attraverso l’utilizzo del comando “SOLO GRIGLIA” ho potuto impostare una griglia tridimensionale, come base, che mi permettesse di orientarmi nello spazio e disegnare la mia trave. Giacché le aste dovevano incontrarsi in un punto, ho preso in esame un “Passo Griglia” di 0,5 m per ogni direzione, così da generarmi l’interesse del mio ideale metro quadrato studiato.

 

• Attraverso il comando “ASTA” ho disegnato il modulo piramidale principale che poi ho opportunamente copiato e incollato, con un passo regolare di 1 m, nelle direzioni X e Y, per 20 volte. 

Una volta disegnata la trave alcuni passaggi fondamentali sono necessari per terminare lo studio strutturale su SAP.

 

• Seleziona tutte le aste --> Assegna Frame --> Rilasci/Semincastri --> “ ASSEGNA RILASCI FRAME" --> Momento 22, Momento 33 : Inizio = 0 / Fine = 0 e Torsione : inizio = 0 --> Ok.

 

• Dopo che abbiamo rilasciato tutti i frame che ci interessano, così da intervenire su tutti i nodi (considerati inizialmente come incastri) trasformandoli in cerniere interne, dobbiamo ora assegnare una tipologia di sezione e un materiale a tutte le aste: Definisci --> Proprietà sezione --> Sezione frame --> “PROPRIETA’ FRAME" --> agg. Nuova Proprietà --> in questo caso io ho scelto: Steel e tubo circolare --> Assegno un: Nome sezione e materiale ( A992FY50 = acciaio) --> Ok. 

 

• Adesso assegno i vincoli esterni. In questo caso ho ipotizzato che a distanza 5x5 metri interni, da ogni angolo della piastra, si costruissero quattro cerniere esterne a sostegno della struttura reticolare: Seleziona i punti prescelti --> Assegna --> Nodo --> Vincoli esterni --> Scegli il vincolo predefinito (in questo caso ho scelto quattro cerniere) --> Ok. 

 

• Una volta sistemati i vincoli esterni, le cerniere, applichiamo, in questo studio alla sola superficie superiore, i carichi esterni, le “forze nodali”. Quando la struttura è molto articolata, come quella presa in esame, è opportuno adottare questa strategia per selezionare in un attimo ogni punto su un piano stabilito: Seleziona --> Seleziona --> Specificazione Coordinate --> Clicca Nodo nel Piano XY àseleziona un nodo di riferimento su tale piano. 

 

• Ora posso assegnare i carichi: Assegna --> Carichi Nodo --> Forze --> + --> Agg. Nuovo Schema Carico --> Assegna nome schema carico e peso proprio = 0 --> Associa alla Traslazione Globale Z il valore ipotizzato da progetto preliminare di 20 KN, (in questo caso pari a -20 perché la forza è diretta verso il basso) --> Ok. 

 

• Ora posso avviare l’analisi definitiva con il comando “LANCIA ANALISI”. Imposta Casi Carico da Eseguire --> Esegui/Non Eseguire Casi, per tutte le forze che non voglio prendere in considerazione nel mio studio --> Ok. 

ANALISI.

 

• Per visualizzare i dati tecnici relativi alle forze applicate posso visualizzare le tabelle. Visualizza --> Mostra Tabelle --> Risultati Analisi --> Seleziona Schemi di Carico --> Ok --> File --> Esporta Tabella Corrente --> Excel --> Ok.

 

• Infine, per ritrovare una corrispondenza con la classificazione delle aste in tabella sul disegno di Sap, così da sapere come il programma ha nominato ogni singola asta e riconoscere quelle che ci interessano rispetto allo studio delle tabelle, possiamo, attraverso il comando “VISUALIZZA OPZIONI PER FINESTRA ATTIVA”, inserire nel disegno le designazioni per i nodi e/o per  tutte le aste. 

 

Fine!

A.P.

 

 

 

 

 

 

post di prova!

post di prova! 

A.P.