ESERCITAZIONE 5 CENTRO DELLE RIGIDEZZE

Affrontiamo l’analisi del comportamento di un impalcato, munito dei dovuti controventi, sollecitato alle forze esterne orizzontali, a simulazione delle azioni sismiche, del vento, della spinta della terra, etc., e di conseguenza le risposte dei controventi a tali sollecitazioni.

E’ importante quindi ripartire in modo adeguato le forze orizzontali, in quanto una struttura, nella sua vita tridimensionale, non deve impegnarsi ad affrontare solo le azioni dovute ai carichi verticali.

In questo modo nel momento di cui si progetta una struttura si deve tener presente che gli elementi strutturali hanno questa duplice funzione; ne è un esempio il telaio, il più semplice controvento, costituito da un collegamento in testa ai pilastri, quindi nel piano verticale, che è capace di sopportare sia i carichi verticali che le azioni orizzontali.

Si è deciso di esaminare un impalcato formato da un telaio shear-type, ossia un insieme di travi e pilastri piano, in cui le travi sono elementi infinitamente rigidi a flessione, perciò non si deformano assialmente ma si avrà solo una traslazione orizzontale δ, conseguenza della deformata dei pilastri soggetti a flessione; le travi quindi avranno un momento d’inerzia molto più grande rispetto ai pilastri e i nodi sono tutti rigidi per cui saranno degli incastri.

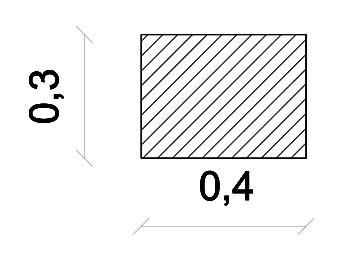
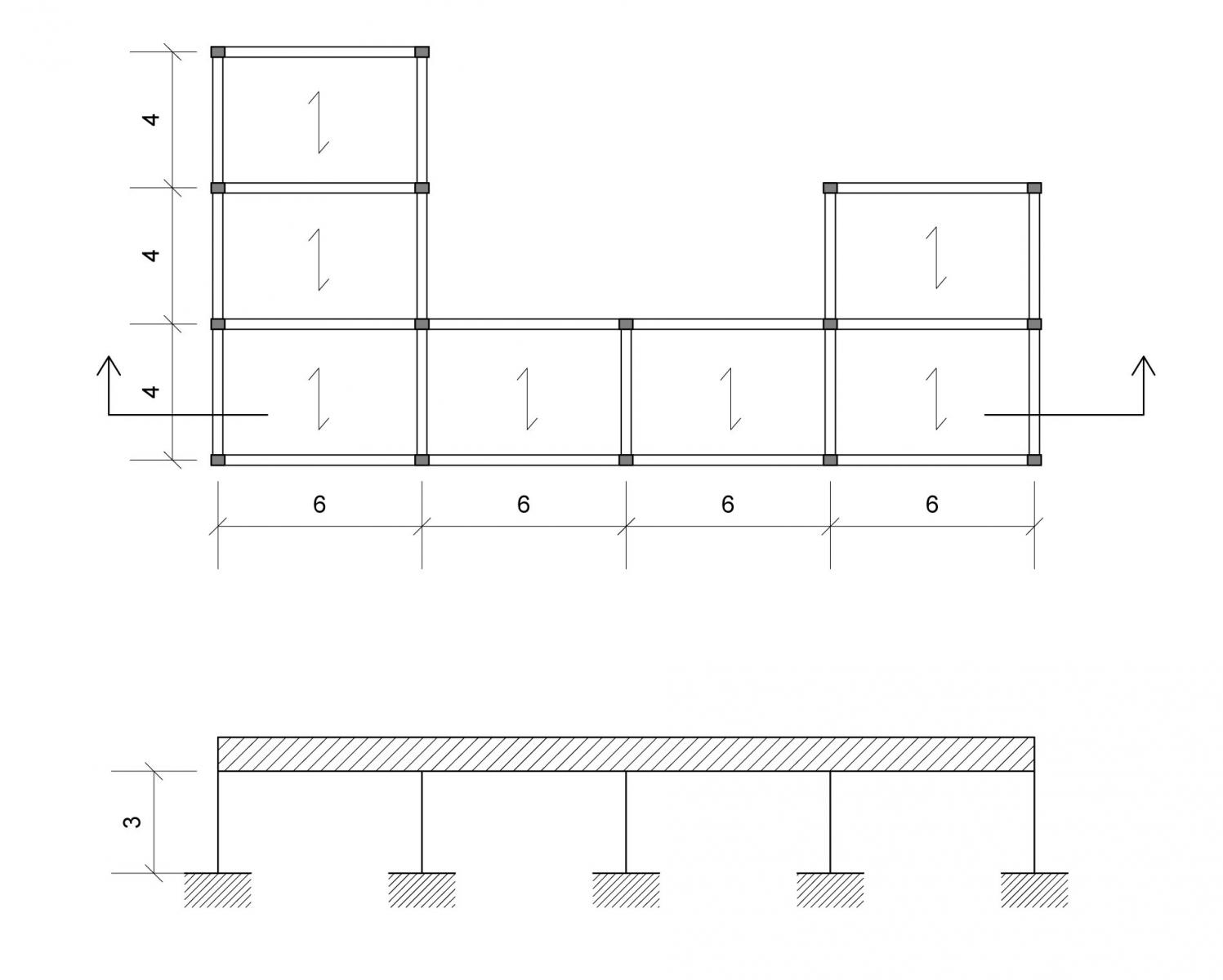
Si ipotizza quindi un impalcato di un piano, come in figura, costituito da 10 telai shear-type, di cui 5 lungo la direzione orizzontale e 5 lungo quella verticale; ogni telaio è costituito da pilastri con sezione (40 x 30) cm e altezza 3 m, e con modulo si inerzia maggiore nella direzione di massima inflessione pari a:

Ix= (b x h^3)/12= (40 x 30^3)/12= 90000 cm^4

Ogni telaio è considerato un controvento, e siccome sono dei vincoli elastici, possiamo rappresentarli come delle molle; il concetto di rigidezza di questi controventi, k, nasce allora nel piano dei prospetti e per comodità la trasportiamo in pianta. Analizziamo quindi come reagiscono gli impalcati a causa delle azioni orizzontali.

Per comodità inseriamo l’impalcato in un sistema di riferimento e indichiamo con kv rigidezza controventi verticali, lungo y, ko rigidezza controventi orizzontali, lungo x, dv distanza orizzontale dei controventi dall’origine degli assi, posto nel pilastro 1, e do distanza verticale dei controventi dall’origine degli assi.

Ogni controvento si prenderà una parte delle forza orizzontale applicata all’impalcato, a seconda della rigidezza dei controventi, come somma delle rigidezze dei pilastri che lo compongono, e della sua distanza dal punto detto centro di istantanea rotazione o centro di rigidezza.

1-Calcolo della rigidezza traslante dei controventi

Si calcola la rigidezza traslante di ogni controvento, come la somma delle rigidezze dei pilastri che lo compongono, considerando che la rigidezza di un pilastro del telaio shear-type è pari a k= 12EI/h^3;

pertanto la rigidezza totale del controvento sarà k_t= 12EItot/h^3, con E= 21000 N/mmq, Ix= (b x h^3)/12=90000 cm^4 e h= 3m

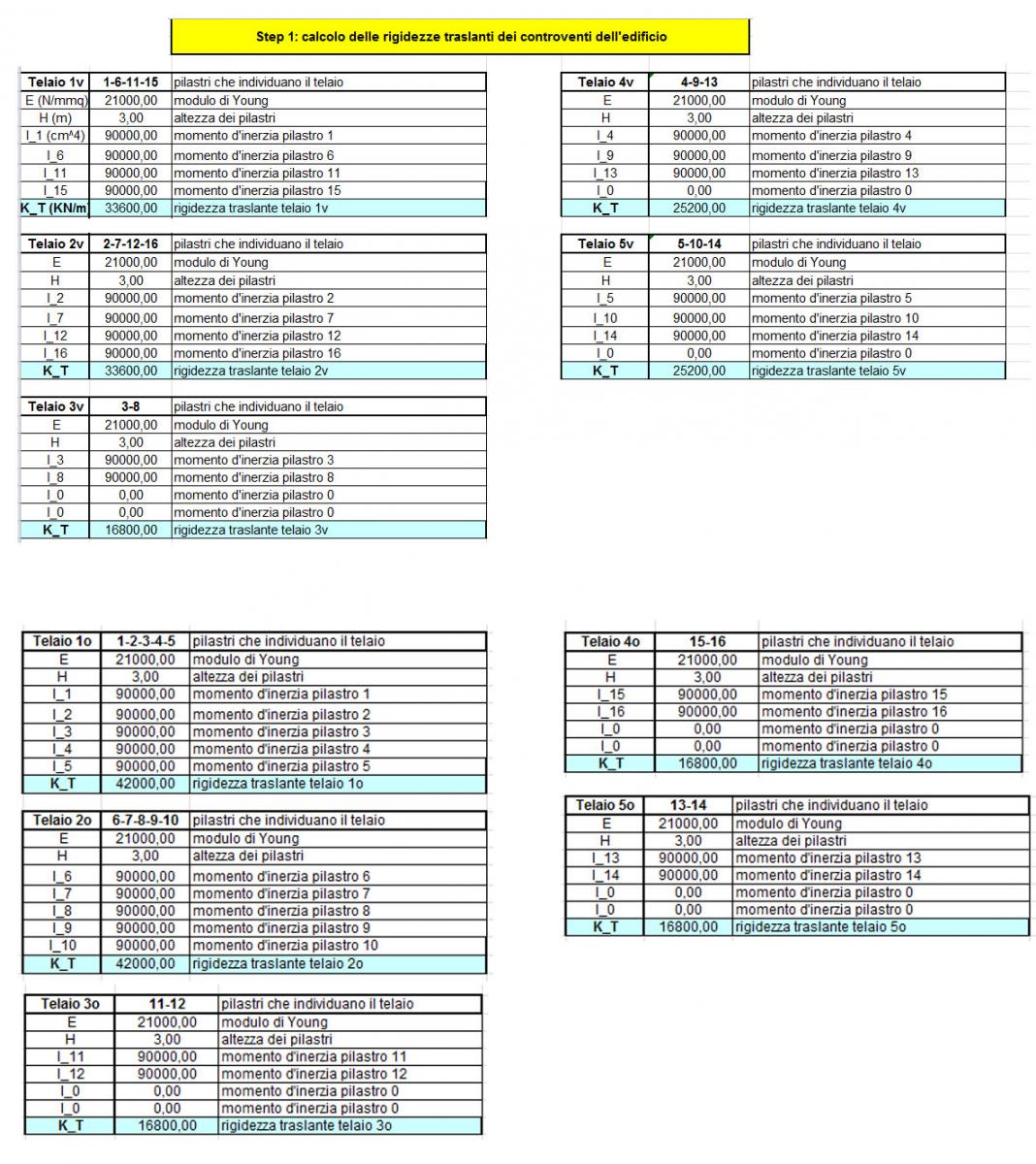
2-Tabella sinottica controventi e distanze

Riassumiamo il una tabella i valori delle rigidezze e le loro rispettive distanze dal punto di origine degli assi.

3-Calcolo del centro di massa

Calcoliamo ora il centro di massa dell’impalcato, come centro dell’area, e siccome siamo di fronte ad un’area più complessa si può dividere in aree geometricamente più semplici e calcolare per ognuno il centro delle masse.

Sappiamo infatti che se la forza applicata all’impalcato ha la retta d’azione passante per questo il centro di massa, l’impalcato non ruoterà ma traslerà solamente, compromettendo quindi in misura minore la sicurezza dell’impalcato, mentre al contrario nel momento in cui la retta d’azione è distante dal centro, l’impalcato ruoterà nel piano.

Per questo motivo è importante quando di progetta un edificio, che centro di massa e centro di rigidezza siamo il più possibile vicini per ridurre al minimo la rotazione dello stesso.

G1 (12;2)

G2 (21;6)

G3 (3;8)

Con G (xG;yG) = (10,71;4,29)

xG= (∑Ai x xG)/Atot

yG= (∑Ai x yG)/Atot

4-Calcolo del centro di rigidezze e delle rigidezze globali

Con C (xC;yC)= (10,88;4,75)

xC= (∑kvi x dvi)/ ∑kvi

yC= (∑koi x doi)/ ∑koi

Calcoliamo poi le distanze dei rispettivi controventi dal centro di rigidezza, è infine la rigidezza a rotazione dei controventi data dalla somma dei prodotti delle rigidezze di ogni controvento e la sua distanza al quadrato rispetto al centro delle rigidezze.

kφ= (∑ki x ddi^2)/ ∑kvi

5-Analisi dei carichi sismici

Calcoliamo infine i carichi sismici partendo dal carico totale gravante sulla area dell’impalcato. Ricaviamo quindi il valore della forza sismica agente sull’impalcato dato dal peso sismico W(KN) e dal coefficiente di intensità sismica c=0,10

F= W x c= 202,61 KN

6-7-Ripartizione della forza sismica lungo x e lungo y

Calcoliamo il momento torcente prodotto dalla forza sismica rispetto al centro delle rigidezze per cui con braccio pari alla distanza tra centro di rigidezza e centro di massa dove è applicata la forza, rispettivamente rispetto all’asse x e all’asse y.

Calcoliamo poi le traslazioni orizzontali e verticali.

uo= F/kotot

vo= F/kvtot

Infine la rotazione dei controventi

φ= M/ kφ

Infine le reazioni vincolari dei controventi da:

Ri= ki x ( u x ddi x φ)

Ri= ki x ( v x ddi x φ)

Dall’analisi fatta sembrerebbe che l’edificio sottoposto alla forza sismica F subisca solo una traslazione, in quanto siccome i due centri, di massa e delle rigidezze, sono abbastanza vicini, portano ad una rotazione quasi nulla. Verifichiamo ora anche su SAP.

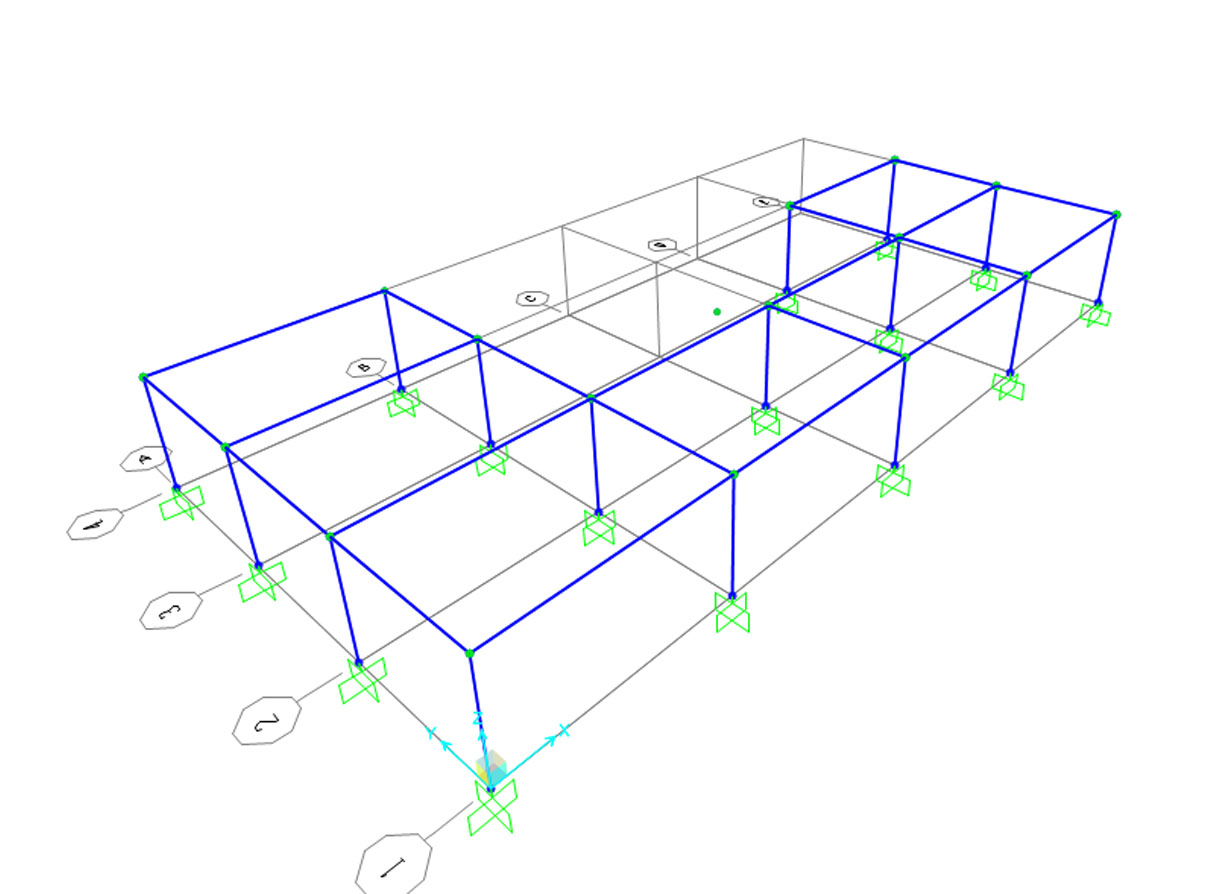
Si disegna l’impalcato su sap e indichiamo che i vincoli a terra sono incastri

Definiamo la sezione delle travi, che saranno abbastanza alte per simulare un telaio shear-type.

Si assegna la sezione ai pilastri.

Si disegna il centro delle rigidezze

Definiamo ora che il punto disegnato fa parte dell’impalcato e che quest’ultimo è di tipo rigido attraverso il vincolo interno (constrain) DIAPHRAM, che attribuisce all’intero impalcato una rigidezza tale ma non ammettere deformazioni ma sono traslazioni.

Per aumentare ancora di più la rigidezza del solaio possiamo aumentare il modulo di inerzia delle travi.

Infine applichiamo la forza sismica nel centro delle rigidezze.

Possiamo avviare a questo punto l’analisi da cui possiamo ricavare la deformata dei pilastri dovuta alla forza F, ad “s” tipica del telaio shear-type, che sta ad indicare un diagramma del taglio costante e un diagramma dei momenti lineare ed in particolare a forma di “farfalla”.

Possiamo anche notare che il centro di rotazione come previsto subirò solo una piccola traslazione e non ruoterà nel piano.