Esercitazione 4: Ripartizione delle forze sismiche

La seguente esercitazione ci è stata utile per affrontare il problema del comportamento di reazione che una struttura ha se sottoposta a carichi orizzontali, quali il sisma o il vento, quesito che va necessariamente messo in relazione con i concetti di centro delle rigidezze e di spostamento rigido.

Si è scelto di analizzare una struttura con intelaiatura trave-pilastro in cemento armato, avente la seguente carpenteria:

Avendo concepito le travi come elementi infinitamente rigidi a flessione, dunque indeformabili, possiamo considerare la struttura scelta come facente parte della tipologia idealizzata di telaio “shear-type”, avente nodi trave-pilastro rigidi, a incastro. Questa tipologia strutturale risponde meglio alle forze orizzontali, rispetto ad una tipologia intelaiata i cui collegamenti trave-pilastro sono incernierati: in questo caso, i pilastri, sottoposti a carichi orizzontali, tendono a deformarsi come se fossero mensole, nel caso scelto, invece, le travi, progettate come elementi molto alti e, quindi, robusti, “spingono” i pilastri a lavorare come elementi di un portale generico: la continuità strutturale data dal nodo incastro favorisce, infatti, un comportamento di collaborazione tra elementi verticali (pilastri) e trasversali (travi), creando ciò che viene definito un controvento.

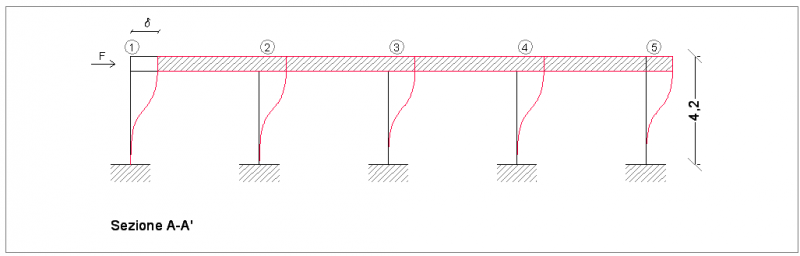
La sezione A-A’ in basso mostra la deformata generalizzata dei sistemi shear-type, oltre ad evidenziare l’altezza dei pilastri scelti, dato fondamentale quando si affronta il problema della rigidezza: sappiamo, infatti, che la rigidezza di un pilastro facente parte di un sistema di controvento shear-type è pari a k=12EJ/L^3, dove E= modulo di elasticità dipendente dal materiale scelto, (nel nostro caso E=24855 Mpa, scelto in conformità a quanto previsto dal programma SAP2000 che utilizzeremo nella fase finale di verifica dell’esercitazione), J= momento di inerzia di sezione del pilastro (cm^4), ed L= all’altezza nel caso di elementi verticali, dunque uguale ad H nel nostro caso. Dalla formula si evince che più un pilastro è basso e più la sua rigidezza sarà elevata, essendo questi due parametri inversamente proporzionali tra loro, di conseguenza più un pilastro è alto e più la sua rigidezza sarà minore, tra l’altro L nella formula è un termine elevato al cubo, ciò significa che l’indiretta proporzionalità che sussiste tra queste due grandezze è regolata da un potenza al cubo e quindi che se l’altezza del pilastro cresce, la sua flessibilità (coefficiente inverso alla rigidezza) aumenta esponenzialmente di ben tre volte.

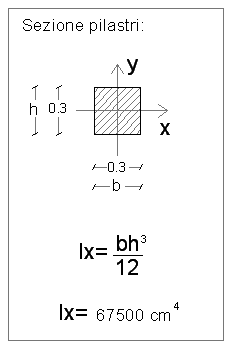
In basso riporto la sezione dei pilastri, ipotizzati di 30x30 cm, con il loro momento di inerzia Ix, altro dato strettamente legato al concetto di rigidezza, in quanto direttamente proporzionale ad essa. 

Essendo la struttura come composta da elementi piani, possiamo considerare  il solaio come un unico corpo rigido inquadrato in un piano X-Y, di cui stabiliremo il punto di origine O (0;0), e considerare i controventi come vincoli elastici cedevoli, e rappresentarli allora come molle sottoposte a forze concentrate, il cui comportamento è regolato dalla Legge di Hooke che stabilisce che una forza F agente su una molla fa nascere una reazione della molla stessa uguale e contraria, pari ad F= ku, dove k è la rigidezza della molla e u individua lo spostamento, o meglio l’allungamento o l’accorciamento cui la molla è stata sottoposta, a seconda che la forza sia di compressione o di trazione.

Di seguito l’impalcato ed i vincoli elastici ognuno indicato con la propria rigidezza, che sarebbe cioè la rigidezza totale del telaio cui corrispondono, data dalla somma delle rigidezze dei pilastri che ne fanno parte (kv1, kv2, etc…).

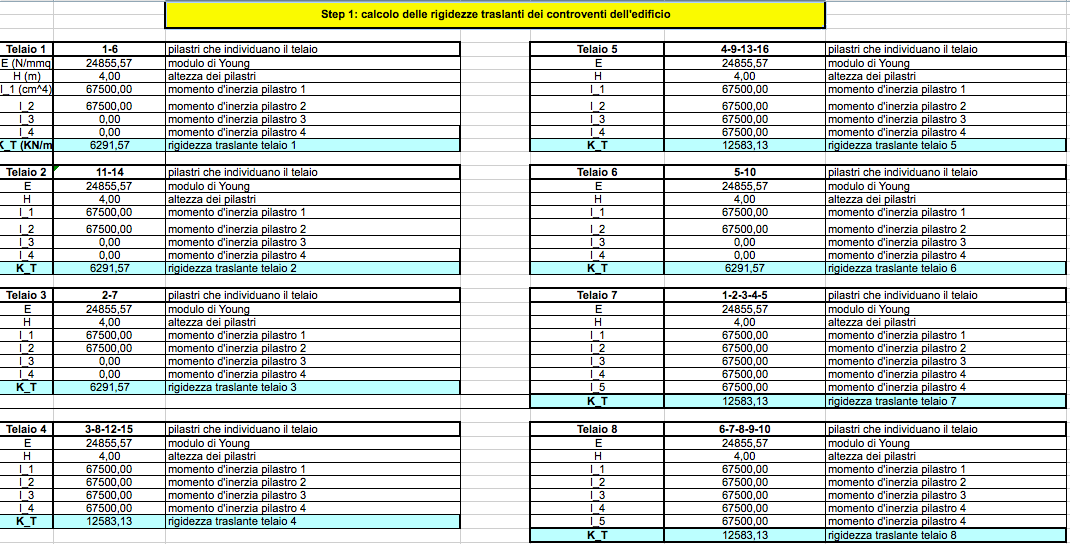
Disponendo a questo punto di tutte i dati costituenti le caratteristiche geometriche e intrinseche della sezione dei pilastri, possiamo iniziare a compilare la prima parte (STEP 1) della tabella excel, che ci aiuterà a situare la posizione del centro di massa e del centro delle rigidezze. Di seguito le tabelle contenenti il calcolo della rigidezza traslante di ogni controvento, verticale e orizzontale, della struttura scelta:

A questo punto, si è passati allo STEP 2, in cui si sono riportate tutte le rigidezze dei controventi e la loro distanza dal punto di origine O (0;0) prefissato arbitrariamente all’inizio:

Si è giunti, quindi, al calcolo delle coordinate spaziali nel piano X-Y del centro di massa, cui è preceduta una fase di suddivisione dell’impalcato in tre aree chiuse e di individuazione delle coordinate dei rispettivi baricentri di quest’ultime, valori che, poi, sono stati inseriti nella tabella dello STEP 3:

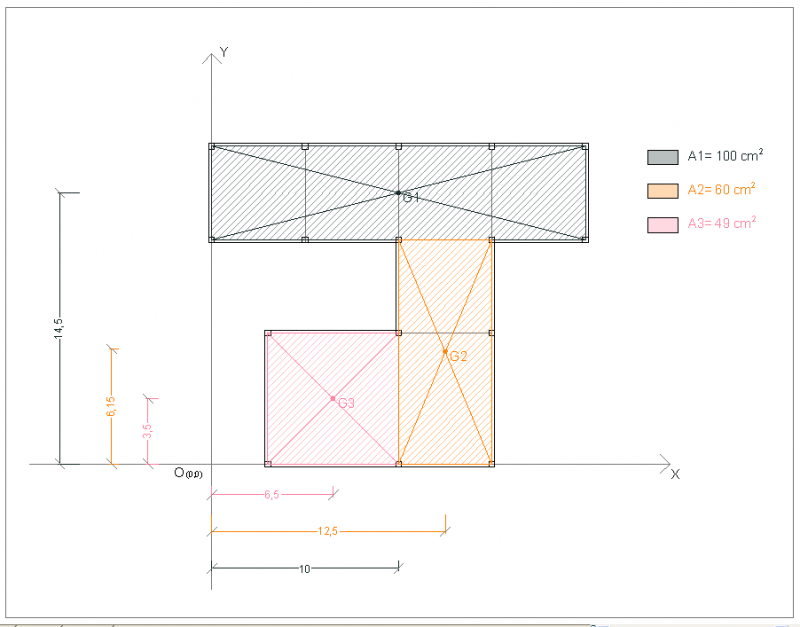
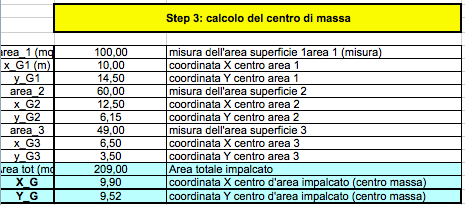
Le coordinate del centro di massa G (X_G; Y_G) sono state ricavate in questo modo:

X_G= Sommatoria coordinate dei tre centri lungo X moltiplicate ognuna per le rispettive aree, il risultato diviso per l’area totale (Atot=A1+A2+A3)=∑ XiG*Ai/Atot

Y_G= Sommatoria coordinate dei tre centri lungo Y moltiplicate ognuna per le rispettive aree, il risultato diviso per l’area totale (Atot=A1+A2+A3)= ∑ YiG*Ai/Atot

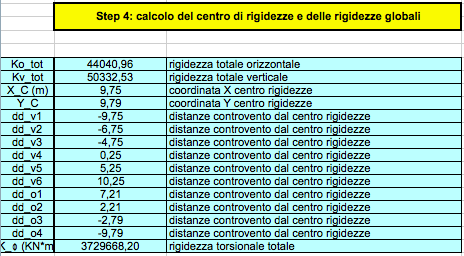
A questo punto si è affrontato lo STEP 4 della tabella excel, mirato al calcolo della rigidezza traslante orizzontale totale Ko_Tot e della rigidezza traslante verticale Kv_tot, entrambe ottenute rispettivamente tramite la somma delle singole rigidezze dei controventi orizzontali e la somma delle singole rigidezze dei controventi verticali. Lo STEP 4 è servito fondamentalmente a stabilire le coordinate del centro delle rigidezze C (X_C;Y_C), ottenute, un con la stessa metodologia attuata precedentemente per calcolare il centro di massa, cioè sommando i prodotti di ogni rigidezza per la sua distanza dall’origine (orizzontale per quanto riguarda i controventi verticali e verticale per quanto riguarda i controventi orizzontali) e dividendo il risultato per la rigidezza traslante orizzontale totale Ko_Tot nel caso di X_C, e per Kv_Tot nel caso di Y_C.

A questo punto si sono riportate tutte le distanze dei controventi dal centro delle rigidezze, sempre orizzontali per quanto riguarda i controventi verticali e verticali per quanto riguarda i controventi orizzontali. Sommando la moltiplicazione, dunque, di ogni rigidezza per la sua distanza al quadrato dal centro delle rigidezze appena trovato si è ottenuta la rigidezza torsionale traslante K_ϕ (KN*m).

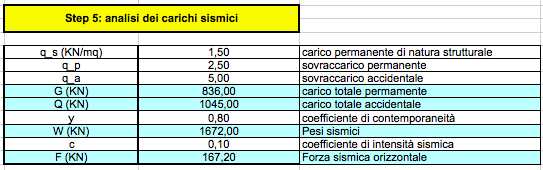
Gli ultimi tre STEP della tabella excel hanno riguardato il calcolo dei carichi sismici e la loro ripartizione lungo l’asse X e l’asse Y.

Dallo STEP 5, abbiamo ottenuto il valore della forza sismica orizzontale F=167,20 KN:

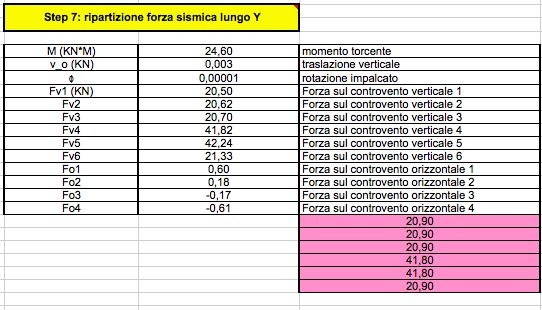
Dallo STEP 6 e 7 abbiamo ottenuto i valori di traslazione orizzontale e verticale della struttura, i suoi valori rotazionali, infinitamente piccoli, oltre ai valori ripartiti dei carichi sismici su ogni controvento, in proporzione alla loro rigidezza:

La seconda parte dell’esercitazione ha riguardato una sorta di verifica dei concetti teorici e, precisamente, si è andato a vedere se, ponendo il centro delle rigidezze come punto di applicazione di una data forza sismica orizzontale, la struttura subisse solo una traslazione, ossia uno spostamento rigido lungo la direzione di applicazione della forza, ma non una rotazione. Viceversa, applicando la medesima forza sul centro delle masse, non essendo esso coincidente con il centro delle rigidezze, si è visto come la struttura tenda a ruotare, creandosi un braccio tra centro delle masse e centro delle rigidezze, ossia tra punto di applicazione della forza e CR. La rotazione in questo caso, tuttavia, è molto esigua, in quanto la distanza, ossia il braccio rotazionale, tra CM e CR è molto piccolo, per questo motivo, per buona norma, si dovrebbe progettare in modo tale da avere questi due punti poco distanti tra loro, così da assimilare le forze orizzontali in maniera più adeguata, sottoponendo la struttura a rotazioni molto poco elevate.

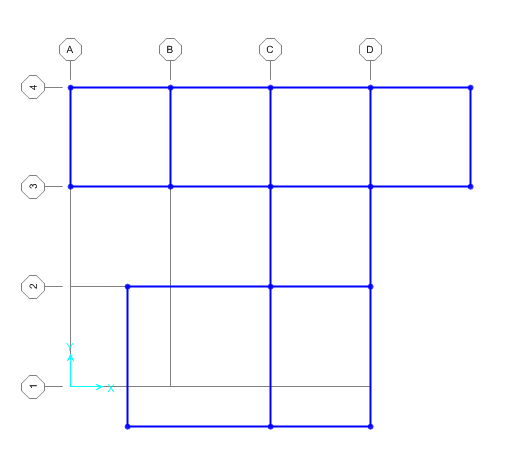
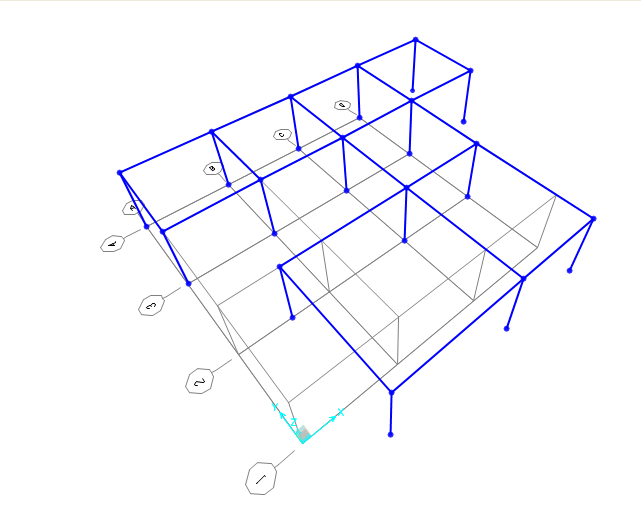
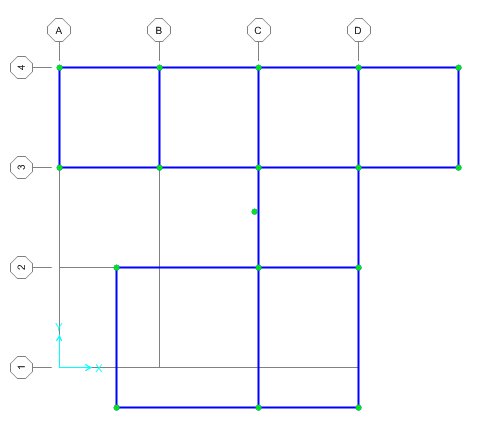
Dunque, si è ridisegnata la struttura su SAP2000. Questa è la sua configurazione in pianta e in prospettiva:

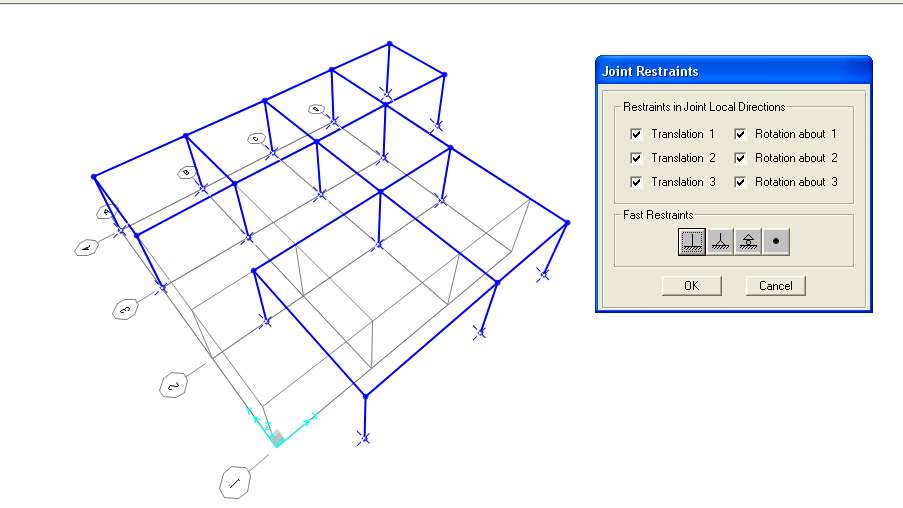
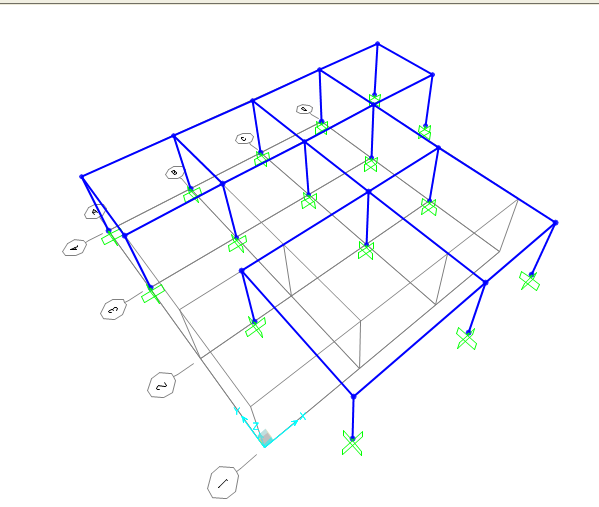
Si sono assegnati i vincoli a terra come incastri, andando su ASSIGN--> JOINT-->RESTRAINTS e selezionando il vincolo incastro:

Successivamente, si sono assegnate le sezioni alle travi, selezionando quest’ultime e andando su ASSIGN-->FRAME->FRAME SECTIONS, si è scelto il cemento armato come materiale (concrete nel programma) e si sono imposte le caratteristiche geometriche di sezione, supponendo di avere un’altezza pari a 60 cm e una base pari a 30 cm. 

Andando poi su SET MODIFIERS, sempre nella finestra di assegnazione delle caratteristiche di sezione, si è aumentato il momento di inerzia aggiungendo tanti zeri, in modo da aumentare la rigidità flessionale delle travi.

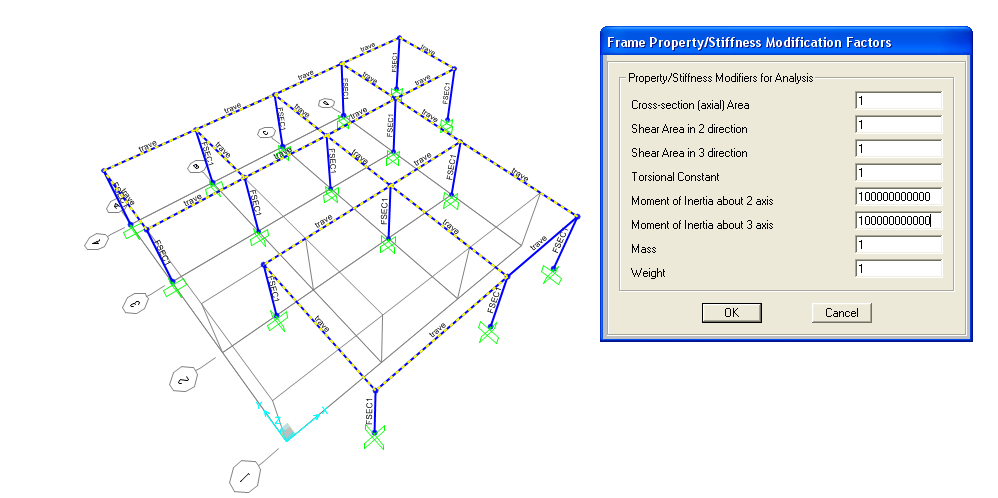Si sono assegnate, poi, le sezioni ai pilastri 30x30 cm:

Questa è la configurazione della struttura con, vincoli a terra, travi e pilastri assegnati:

A questo punto, si è riportato il centro delle rigidezze, utilizzando il tasto punto e assegnato i valori di offset rispetto ai vari assi X,Y e Z:

Per far in modo di generare una continuità strutturale, e, quindi, di considerare come parte di uno stesso piano i punti di incastro trave-pilastro, si sono selezionati e poi si è loro assegnato il comando DIAPHRAGM, andando su ASSIGN-->JOINT-->CONSTRAINTS:

Se il comando ha funzionato, dovremmo ottenere questa schermata, tutti i punti superiori della struttura devono cambiare colore rispetto al resto:

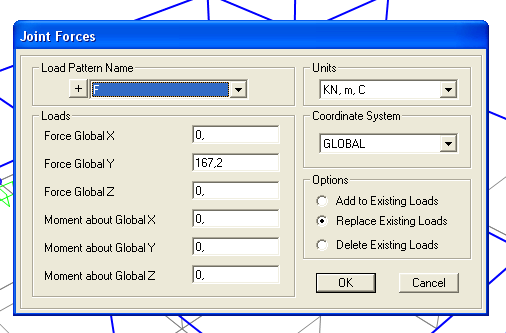
Infine, si è potuta applicare la forza nel centro delle rigidezze, andando su ASSIGN-->JOINT LOADS-->FORCES, assegnando un nuovo livello F (con self multiplier pari a zero) e immettendo un valore lungo l’asse Y pari a quello calcolato tramite l’ausilio della tabella excel:

La deformata ottenuta è stata la seguente:

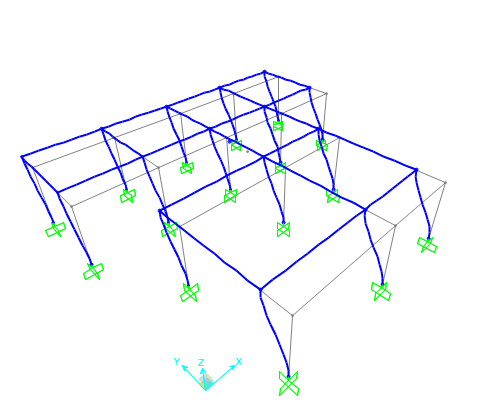
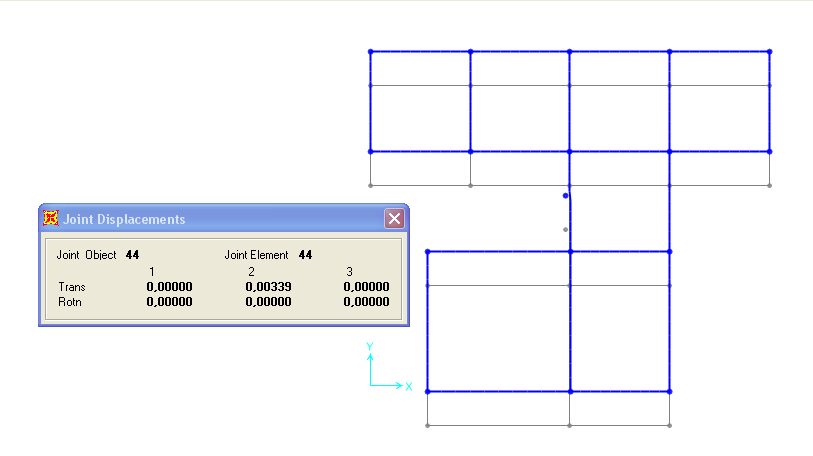
Come si può notare, la struttura è stata sottoposta solo ad un atto di moto rigido, traslando lungo l’asse y, ma non ruotando. Cliccando col destro sul punto che individua il centro delle rigidezze, si è potuto ulteriormente prendere atto del fatto che le rotazioni sono state nulle, ma che c’è stata una traslazione, seppure molto piccola:

Questa è l’andamento lineare a farfalla del momento 2-2, relativo al nostro caso, tipico di un telaio shear-type:

Si è voluto, infine, vedere cosa succedeva nel caso in cui si fosse applicata la forza non nel centro delle rigidezze, ma nel centro di massa e il risultato è stato quello di una rotazione! In basso le fasi di applicazione della forza sul CM e la relativa deformazioni della struttura: