Esercitazione 5 - SOLAIO SHEAR TYPE

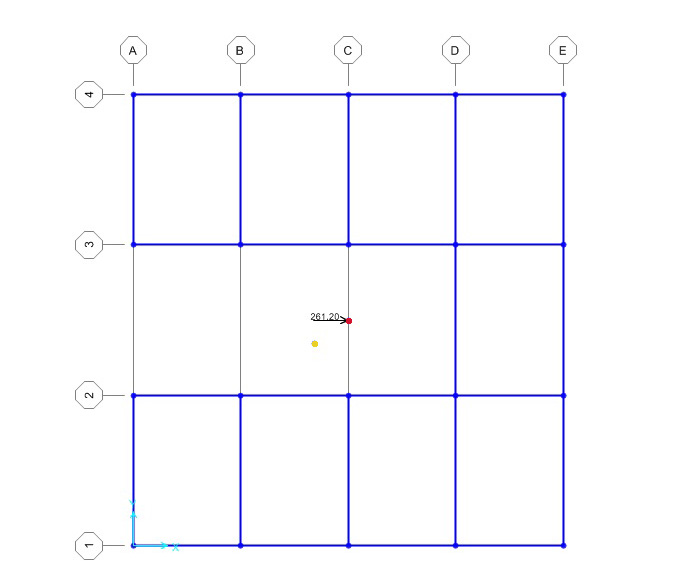
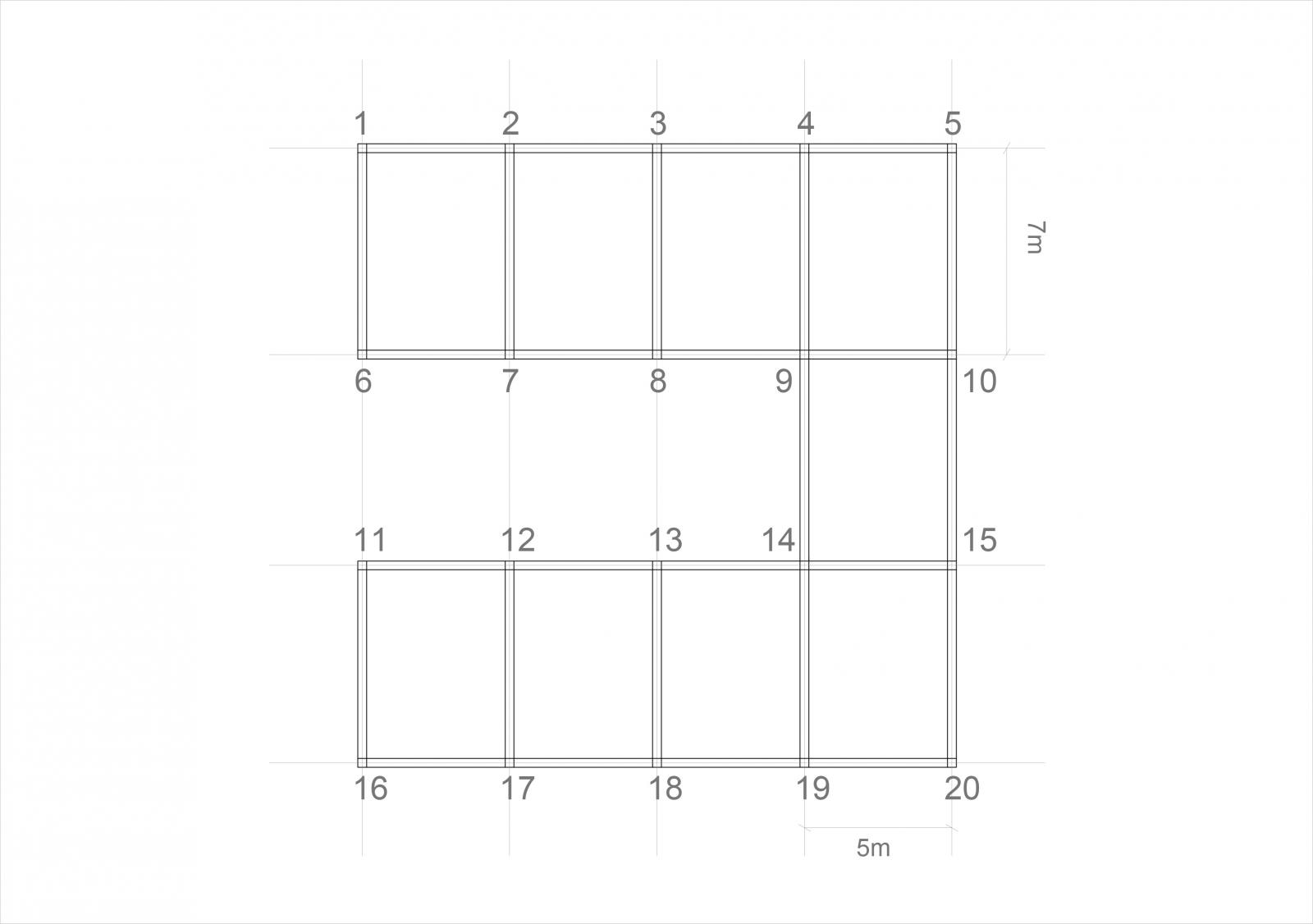
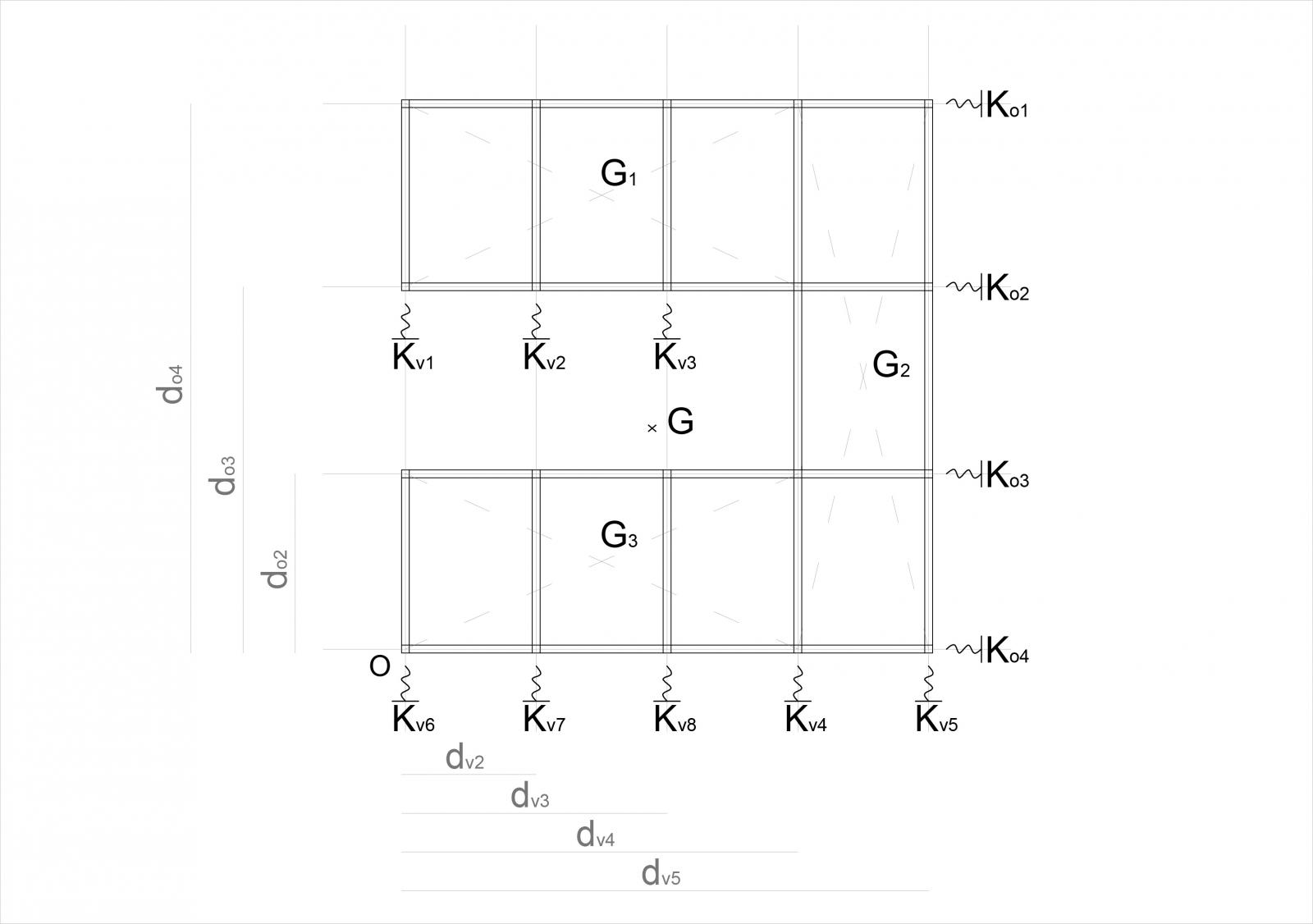
Esercizio per comprendere il comportamento di un controvento rappresentato da un telaio sottoposto a forze verticali e orizzontali. Solaio con 4 impalcati orizzontali e 8 verticali, l’edificio è in cemento armato e cerchiamo di calcolare il centro della rigidezza.

 

Modulo di elasticità E= 2,1 * 10⁵  N/mmq

Altezza dei pilastri H = 3.30 m

Esercizio per comprendere il comportamento di un controvento rappresentato da un telaio sottoposto a forze verticali e orizzontali. Solaio con 4 impalcati orizzontali e 8 verticali, l’edificio è in cemento armato e cerchiamo di calcolare il centro della rigidezza.

 

Modulo di elasticità E= 2,1 * 10⁵  N/mmq

Altezza dei pilastri H = 3.30 m

 

 

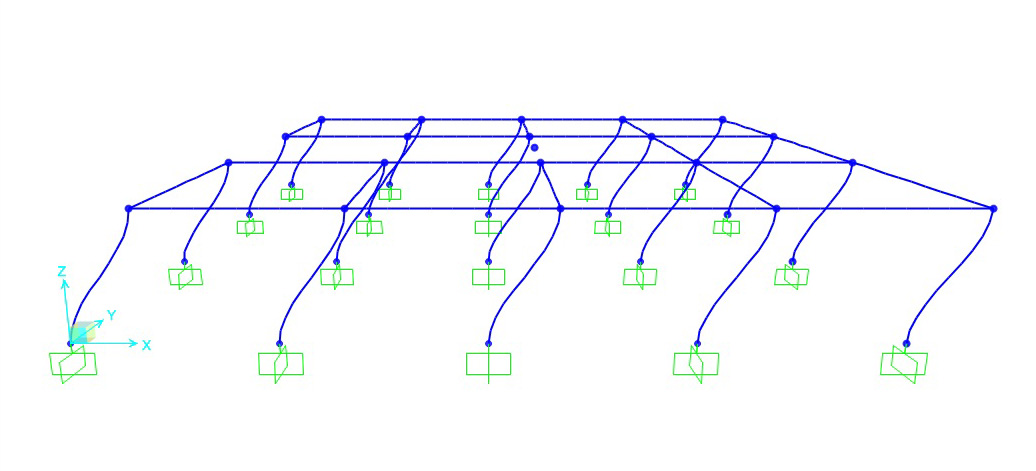
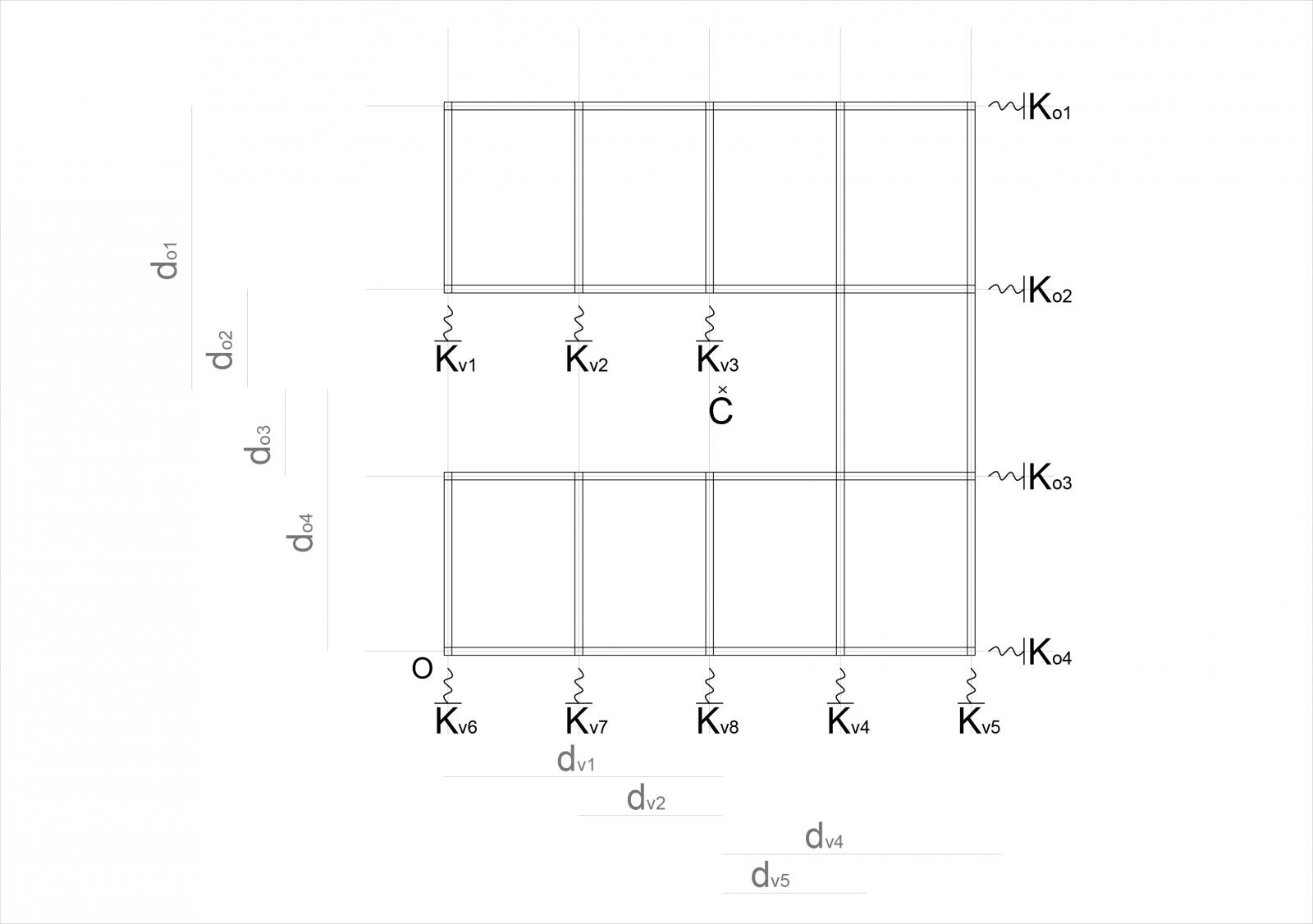
Le reazioni orizzontali vengono disegnate con una molla (avatar) che rappresenta la rigidezza del telaio.

 

Step 1

Calcolo di:

Momento di inerzia dei pilastri I  = b * h ³/ 12 =67500 cm⁴

Rigidezza traslante di ogni singolo telaio K_T =  12 * E * (I_n + I_m + I_w + I_k ) / H³ * 10 ^-5

Il calcolo delle distanze viene fatto sempre in relazione gli assi X, Y a al punto di origine O.

 

 

 

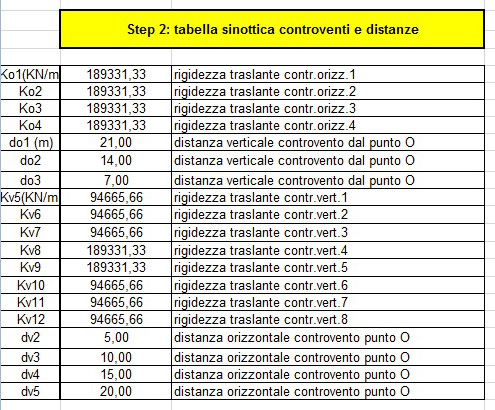
Step 2

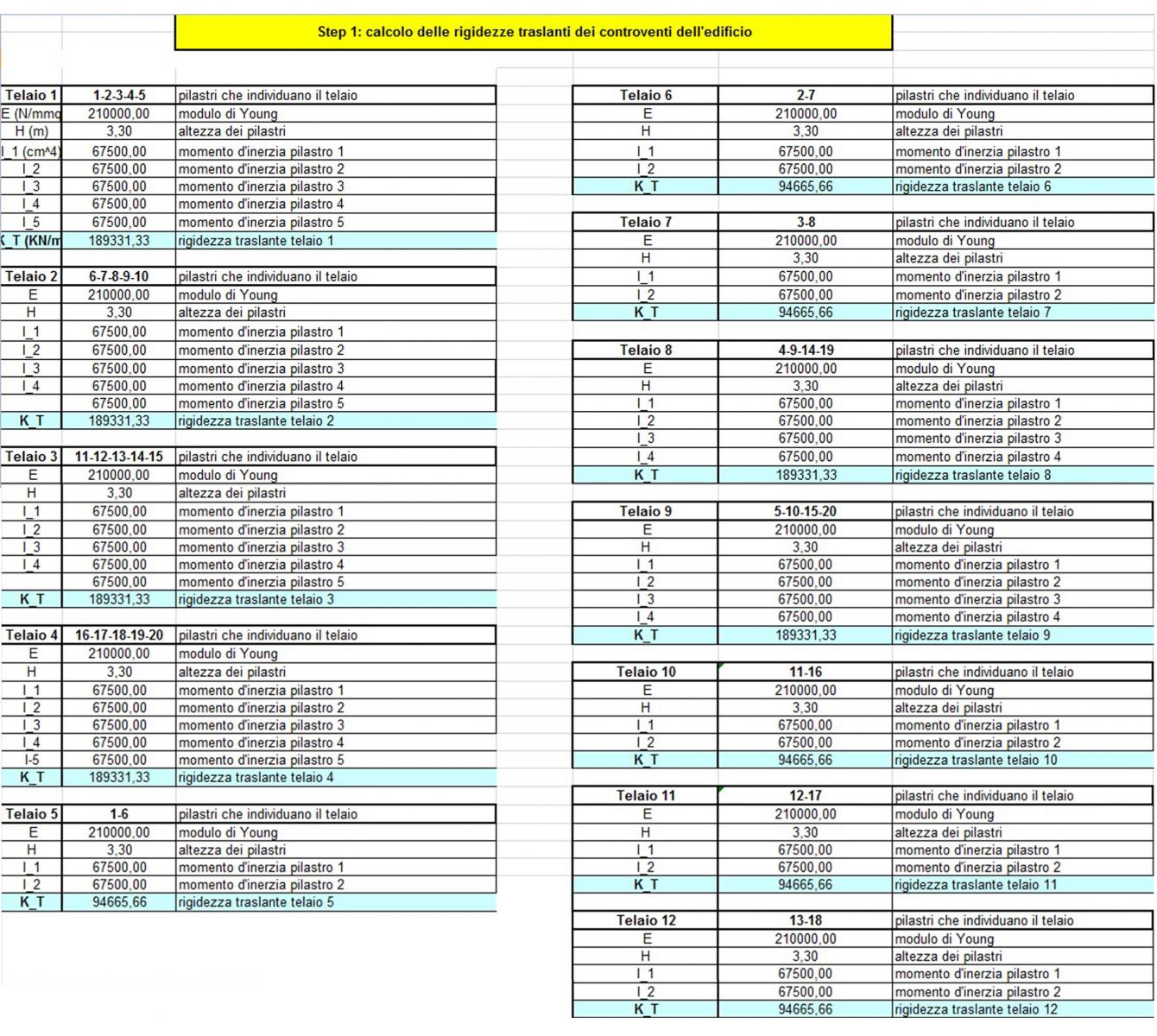
Calcolo di:

Rigidezza traslante dei controventi orizzontali Ko

Distanza verticale dei controventi dal punto O

Rigidezza traslante dei controventi verticali  Kv

Distanza orizzontale dei controventi dal punto O

 

 

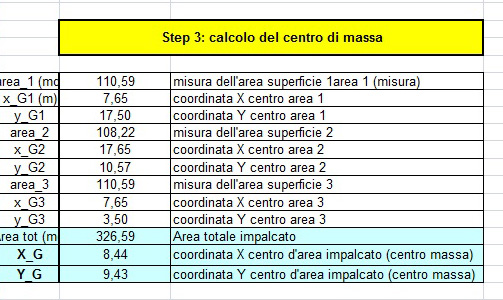
Per il calcolo del centro di massa abbiamo semplificato la struttura in tre superfici più semplici e ne abbiamo calcolati i rispettivi centri di massa. Il calcolo prevede la misurazione dell’area e delle coordinate X, Y di ogni centro dell’area delle superfici.

Step 3

Calcoli di:

Coordinate x ed y di G₁, G₂, G₃.

 

Aree parziali e totale:

Area1 = 110,595 mq

Area2 = 108,225 mq

Area3 = 110,595 mq

Area tot = 326,59 mq

Coordinate generali  del centro dell’area dell’impalcato G:

XG = 8,44 m

Y G= 9,43 m

 

 

 

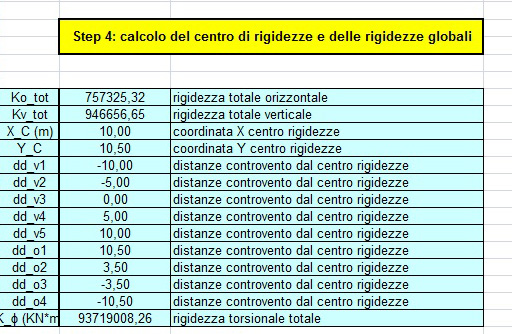
Step 4

Calcolo di:

Rigidezza totale orizzontale e verticale = sommatoria delle rispettive rigidezze traslanti

Distanze dei controventi dal centro di rigidezza  (ddv_n)

Distanze dei controventi dal centro di rigidezza  (ddo_n)

Coordinate X e Y del centro delle rigidezze

Rigidezza torsionale totale  K_ϕ  =  Kv₁ * ddv₁²  + … + Kv_n * ddv_n²  + … +  Ko₁ * ddo₁²  + … + Ko_n * ddo_n²  (KN*m)

 

 

 

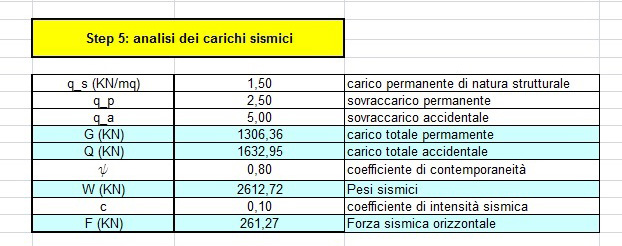
Scegliamo il valore dei differenti carichi (con natura strutturale permanente e accidentale) da cui deriveranno i carichi totali, ripartiti sull’area totale della struttura.

Step 5

Coefficiente di contemporaneità ψ= 0,8

Coefficiente di intensità sismica c = 0,1

 

 

Step 6 – Step 7

Momento torcente M X = c * coordinate del centro delle rigidezze

Momento torcente M Y = c * coordinate del centro dell’area dell’impalcato G

Traslazione orizzontale u = c / Ko tot

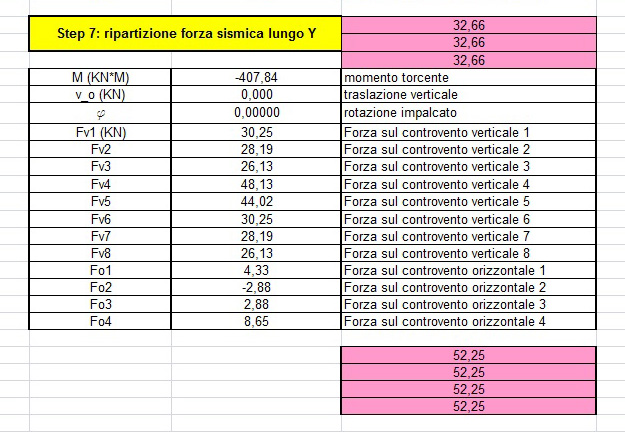
Traslazione verticale v = c / Kv tot

Rotazione impalcato ϕ = M / K_ϕ

Forza del controvento verticale Fv_n = Kv_n * ( v + ddv_n * ϕ )

Forza del controvento orizzontale Fo_n = Ko_n * ddo_n * ϕ

 

Forza del controvento verticale Fv_n = Kv_n *ddv_n * ϕ

Forza del controvento orizzontale Fo_n = Ko_n * ( u + ddo_n * ϕ )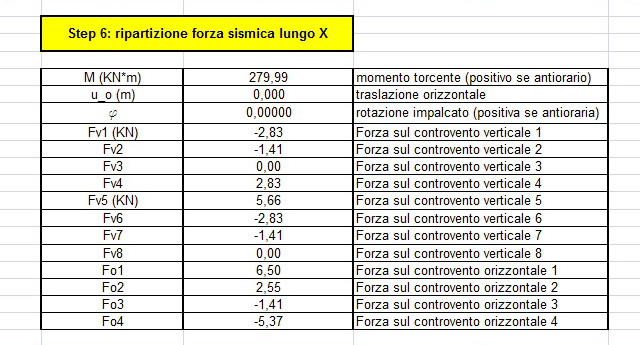

 

Queste sono le immagini dei passaggi su SAP per creare un impalcato SHEAR TYPE:

1. Creo l’impalcato con le dimensioni e le direzioni di quello che ho studiato su exel

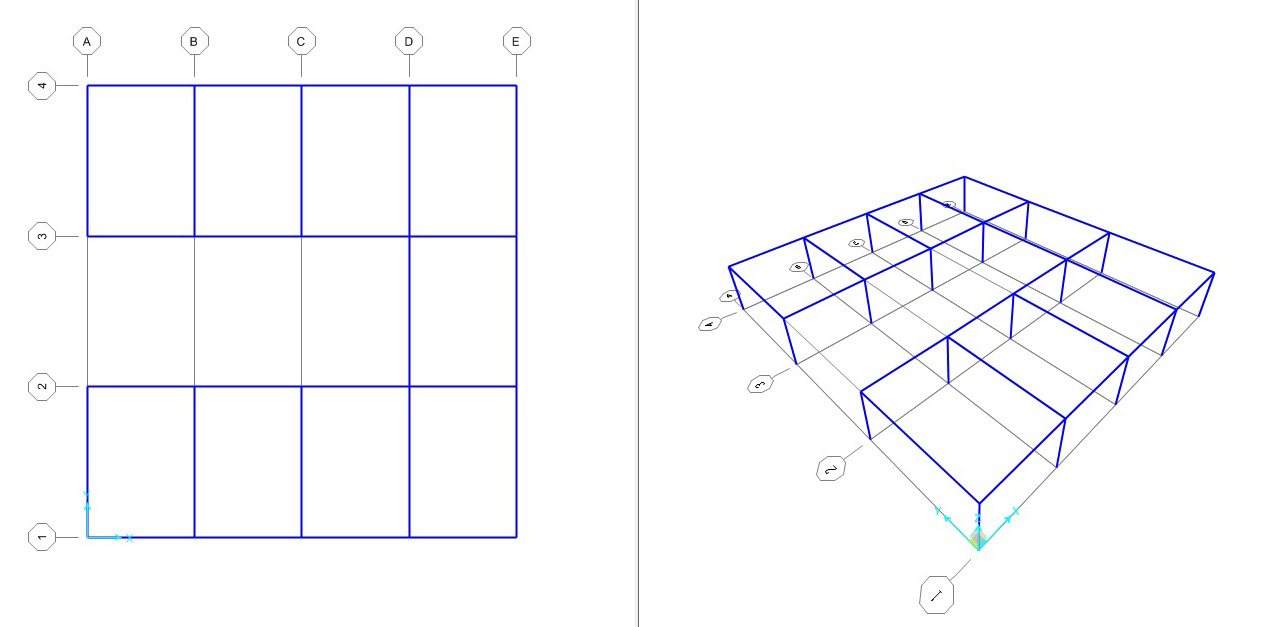
2.Applico degli incastri alle basi dei pilastri

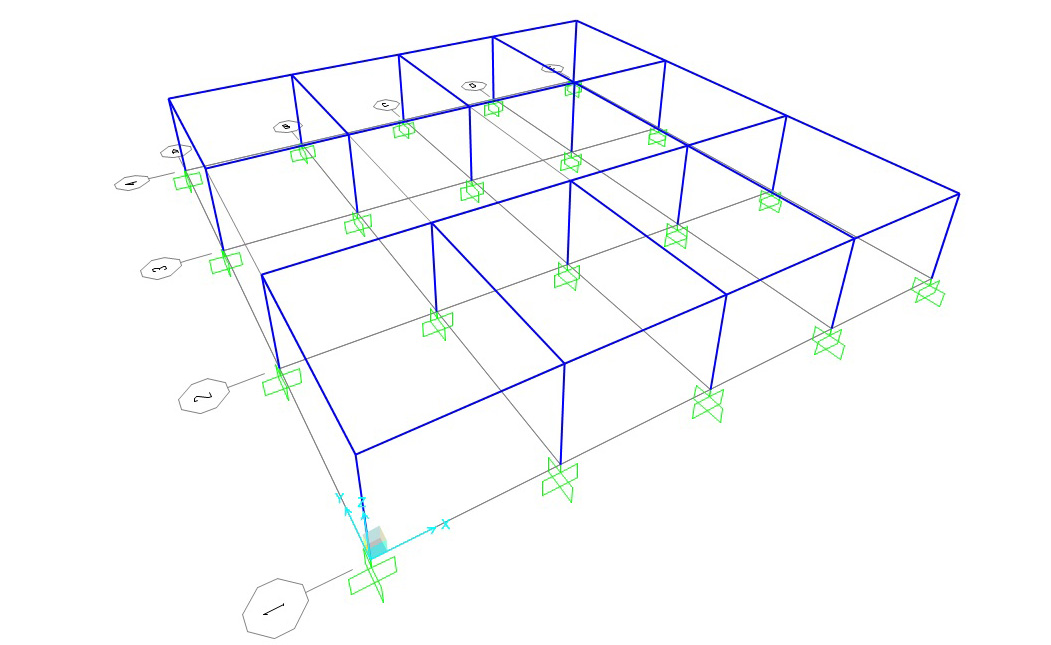
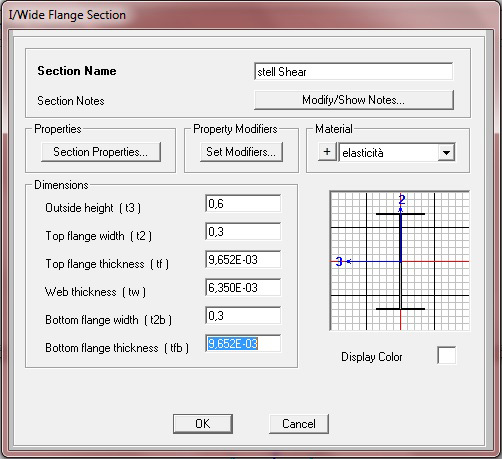
3. Definisco la sezione di pilastri e delle travi Shear

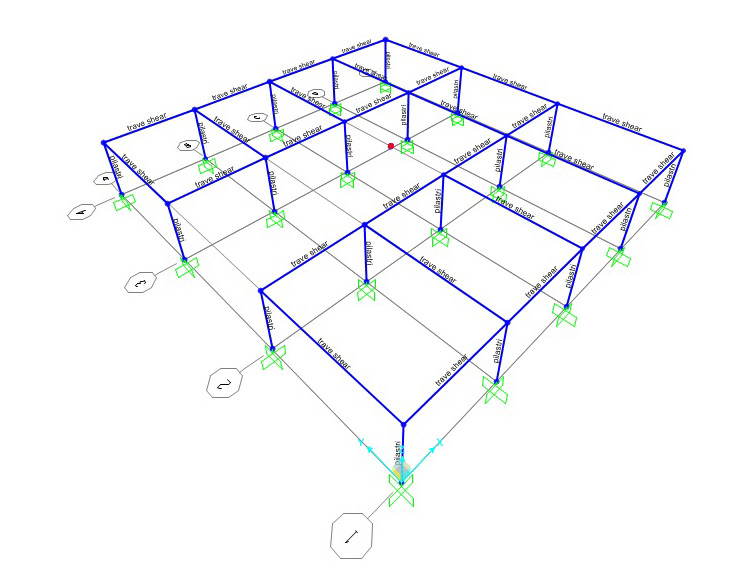
4. Aumento il modulo di elasticità affinché le travi siano Shear type, modificando le proprietà del materiale dell'acciaio

 

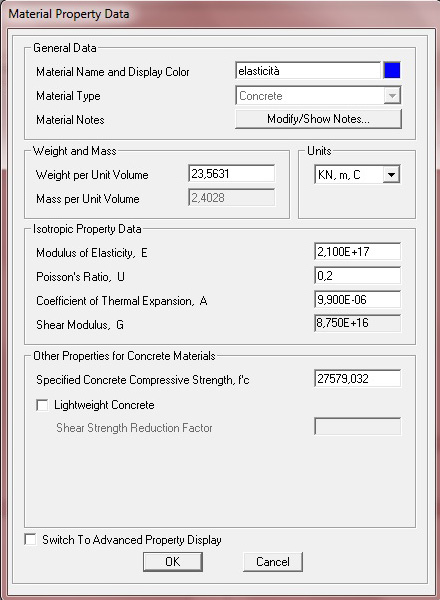
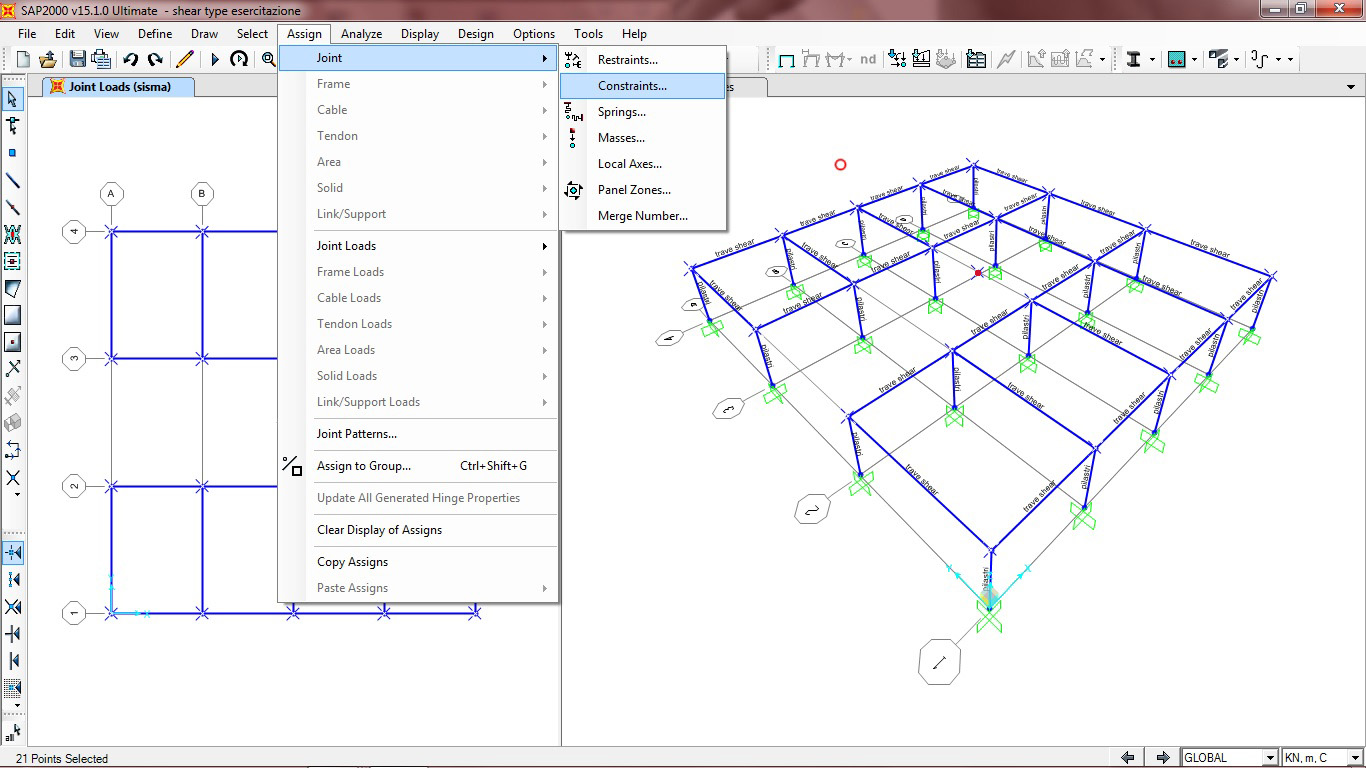
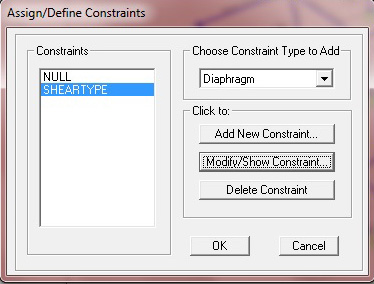
5. Rendo rigida la struttura del solaio unendo tutti i punti e il centro di massa e con Diaphragm

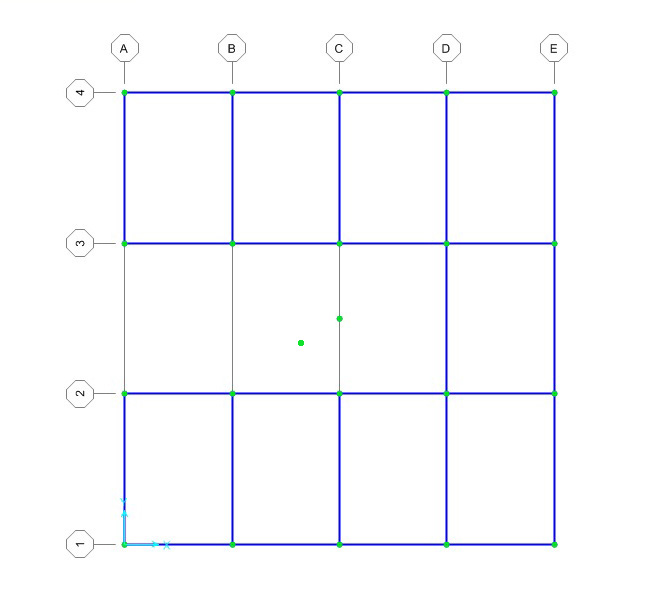
6. Applico la forza in direzione X nel centro delle rigidezze

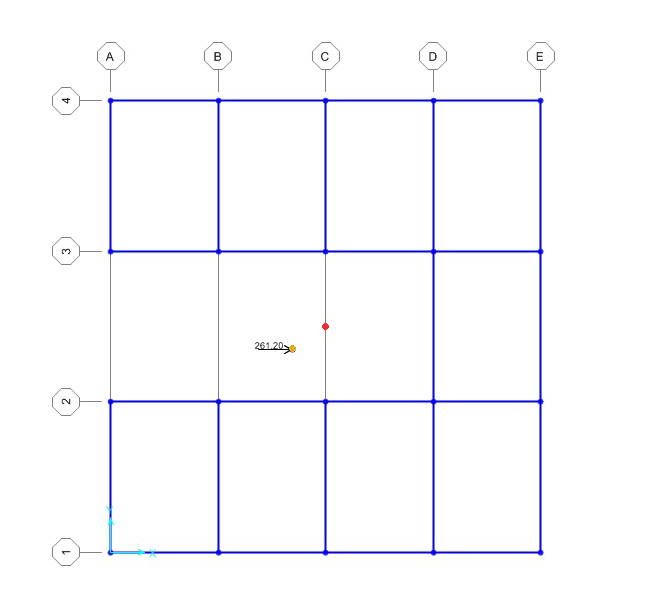
7. Movimento di un impalcato con solaio Shear Type

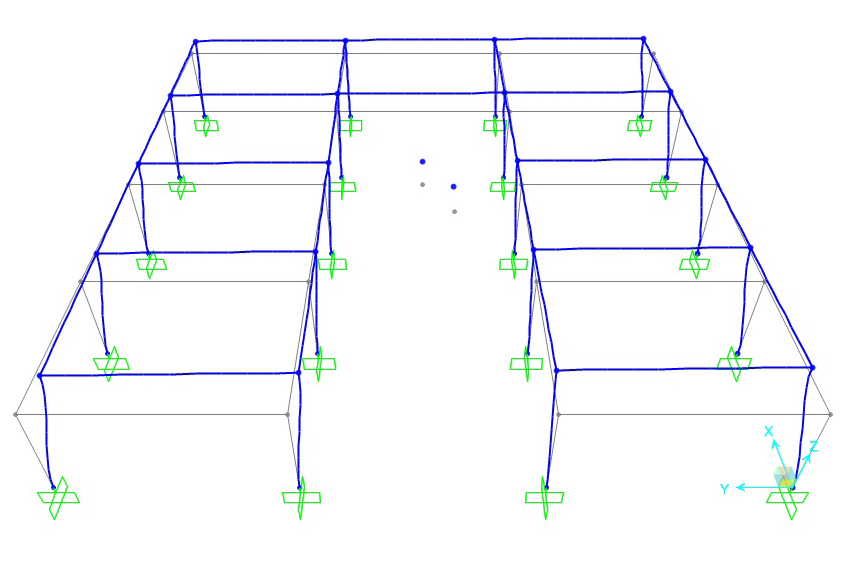
8. Nel caso avessimo applicato la forza nel centro dei massa