Esercitazione_4 | Ripartizione Forze Sismiche e determinazione centro di rigidezza

(eseguito con Giordano Proietti Rocchi)

In questa esercitazione andremo ad analizzare la ripartizione delle forze sismiche in una struttura di un edificio ad un piano. Nella progettazione strutturale non esistono solo le azioni (carichi) verticali, ma anche azioni orizzontali, qualunque sia la loro natura (azioni sismiche, vento, spinte della terra etc.). Le forze sismiche sono forze orizzontali e per far fronte a questo, è necessario dotare l’edificio di controventi; un telaio, se ben pensato in fase progettuale, può resistere oltre che alle azioni  verticali, anche alle azioni orizzontali a cui la struttura è sottoposta, e quindi agire da vero e proprio controvento naturale. Per questo studio adotteremo un impalcato in Cemento armato costituito da telai Shear Type e ne calcoleremo il centro delle masse, il centro delle rigidezze e il suo comportamento quando sottoposto a forza sismica orizzontale.

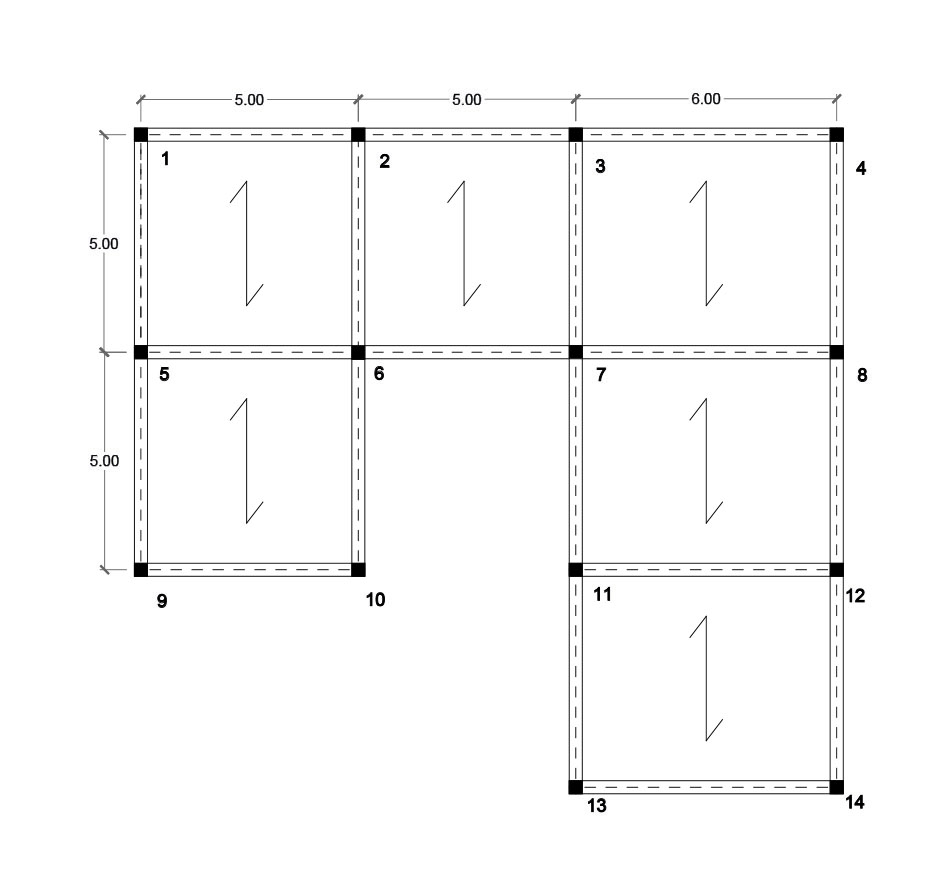
Vediamo ora come costruire ed analizzare un telaio shear type:

1 | Per prima cosa andiamo a disegnare le rigidezze dei controventi orizzontali e verticali (Kv e Ko) dei singoli telai. Per essere rappresentate useremo come esemplificazione una molla, che meglio raffigura la reazione alle spinte orizzontali di questi controventi, aggiungendo anche gli assi X e Y, dato che ci servirà un punto di origine su cui fare calcoli di natura geometrica.

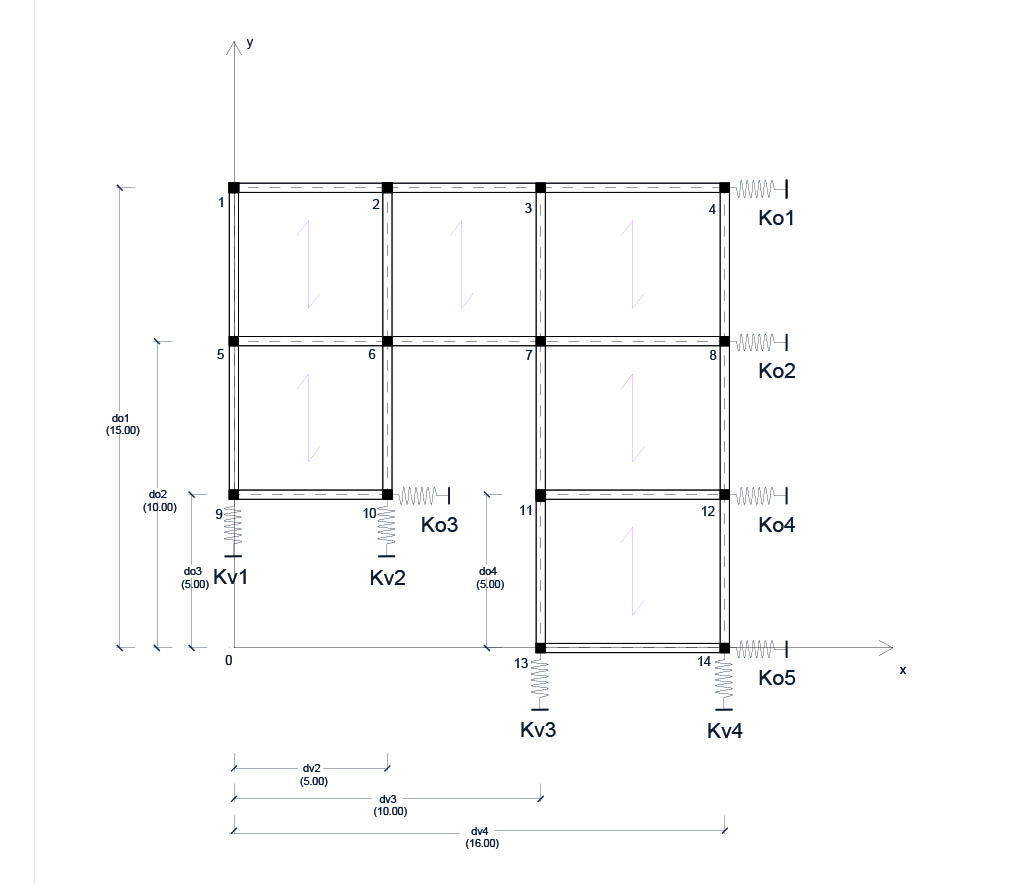 Andiamo ora a riempire con gli opportuni dati richiesti tutta la tabella Excel.

Qui è possibile calcolare il ‘centro di massa’, il ‘centro delle rigidezze’ e la ‘ripartizioni delle forze sismiche’

Primo passo, calcolare la rigidezza di ogni singolo telaio. Per fare ciò, necessitiamo del modulo di Young (a seconda del tipo di materiale che utilizziamo), il momento di inerzia (che ovviamente varierà in base alla sezione) di ogni pilastro, e l’altezza.

Per il momento di inerzia, data la forma quadrata del pilastro, useremo la formula b⁴/12 (b*h³/12 con h e b uguali).

Dati:

[modulo di young] – 25000 N/mm²

[altezza pilastri] – 3 m

[momento di inerzia] – 67500 cm⁴ (sezione quadrata di lato 30 cm)

Dato che il nostro telaio è di tipo Shear-Type la struttura orizzontale è infinitamente rigida e quindi indeformabile assialmente mentre i pilastri sono soggetti a flessione. Il telaio perciò subirà, sottoposto a forze orizzontali, solamente spostamenti rigidi orizzontali senza deformarsi, poiché infinitamente rigido. Solamente i pilastri subiranno una deformazione.

La rigidezza traslante (K) quindi sarà calcolata come:
K=12*EI/h^3

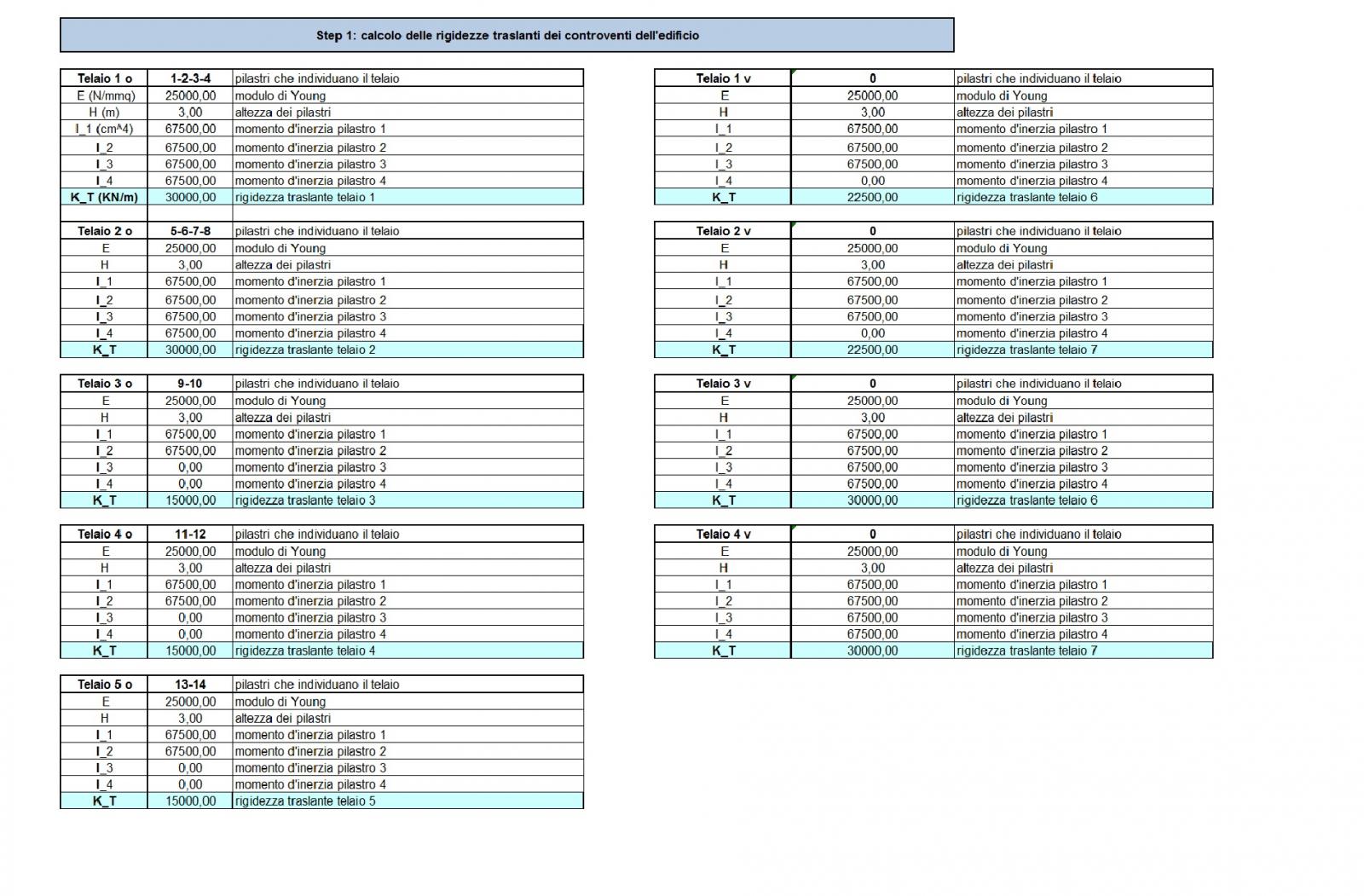
2| Il passaggio successivo è quello di scrivere le distanze ‘orizzontali’ e ‘verticali’ dei singoli controventi rispetto all’origine.

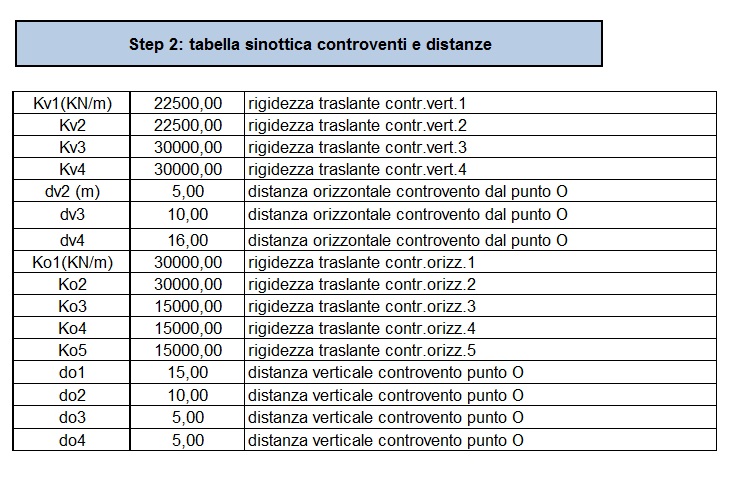
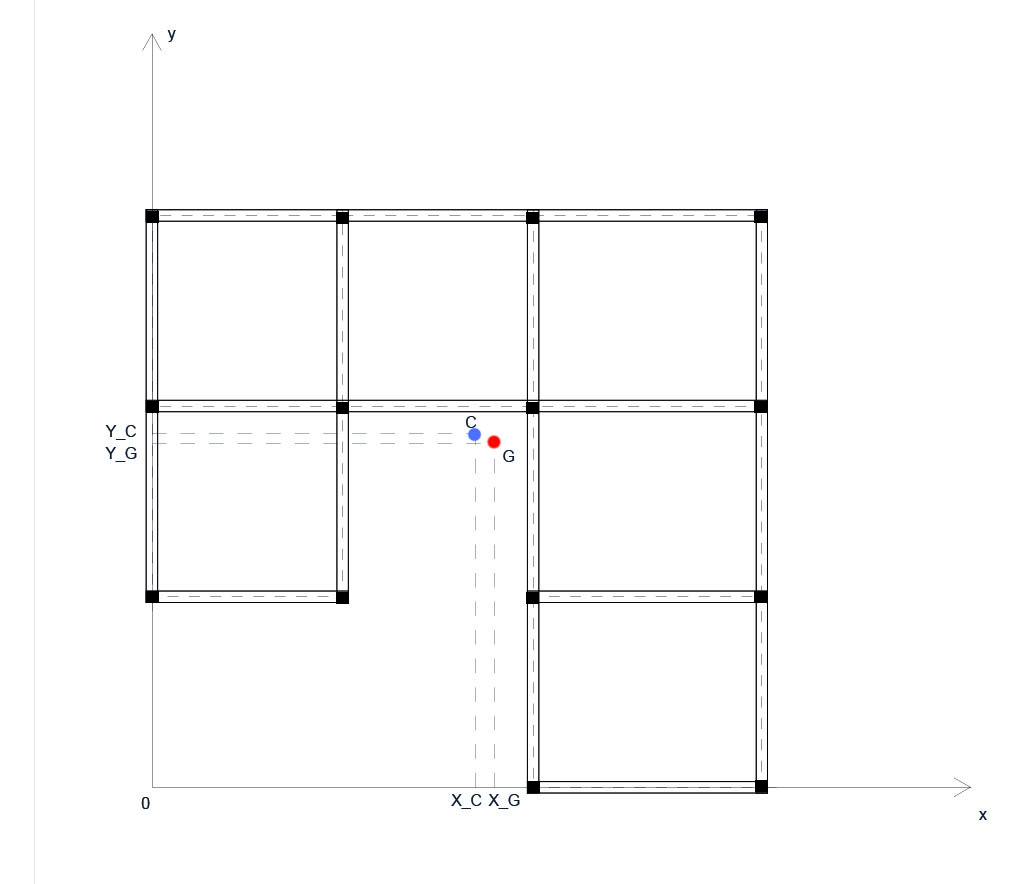
3| Suddivideremo poi il nostro impalcato in figure geometriche semplici, per individuarne i centri geometrici degli stessi e quindi del sistema  (‘centro di massa’).

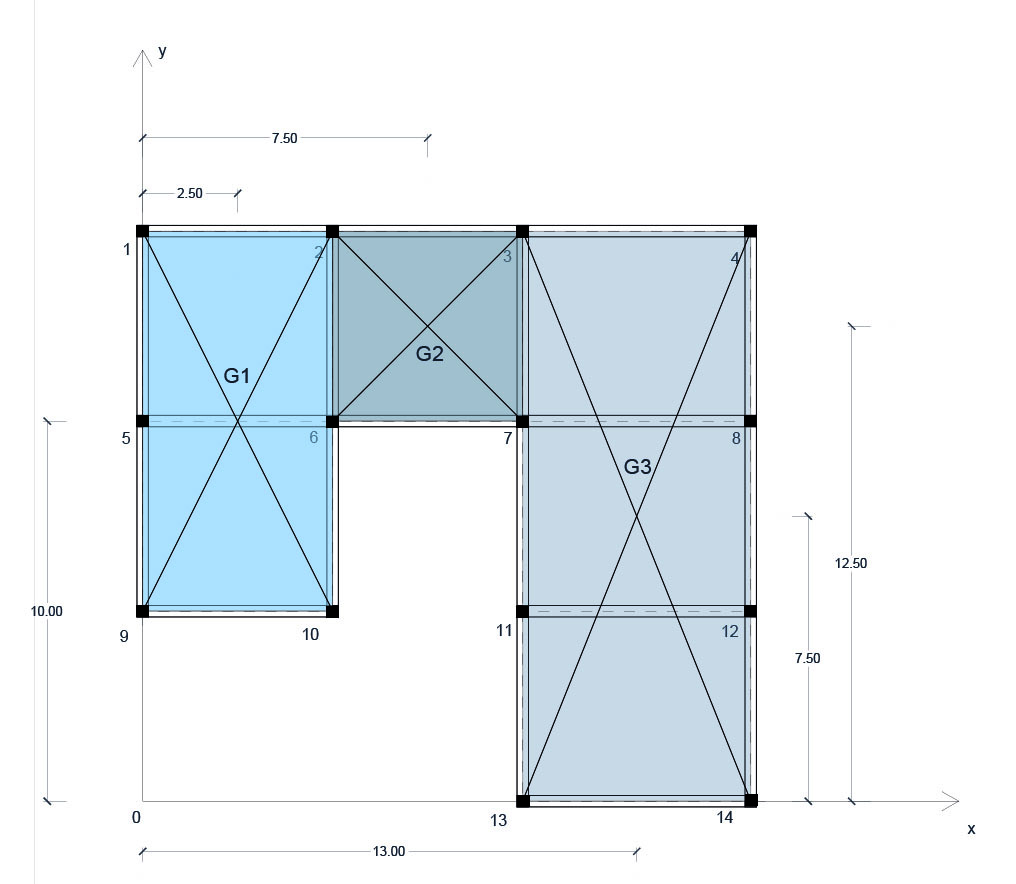
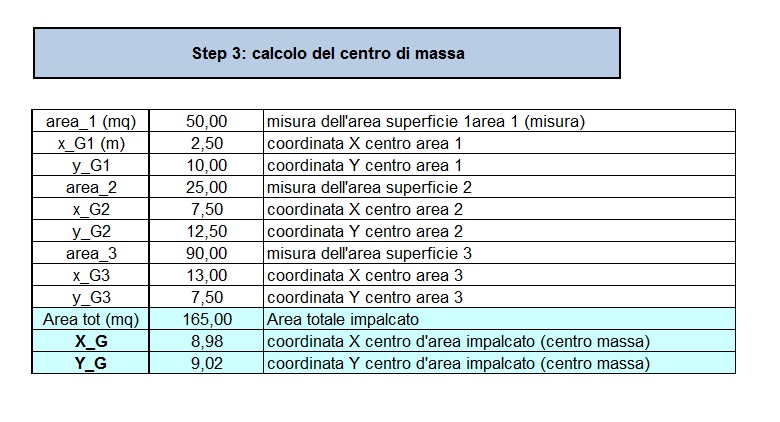
Le cooordinate del centro di massa dell’intera struttura possono essere trovate come sommatoria delle distanze dei singoli centri di massa rispetto agli assi (x o y a seconda di ciò che si vuole calcolare) moltiplicate per le rispettive aree e dividendo il totale per l’area complessiva.

Gmx=∑xG*Ai/Atot

Gmy=∑yG*Ai/Atot

4| Calcoliamo ora le coordinate del ‘centro di rigidezza’, e le distanze di ogni singolo controvento da queste e per trovare le coordinate procederemo allo stesso modo, calcolando a sommatoria del prodotto tra le rigidezze di ogni controvento per le rispettive distanze (verticali o orizzontali in base alla coordinata da trovare) il totale diviso la rigidezza verticale o orizzontale totale. 

Grx=∑Kvi*dvi/Kvtot

Gry=∑Koi*doi/Kotot

Troveremo cosi la rigidezza torsionale totale della struttura.

Kγ = ∑Ki*di²

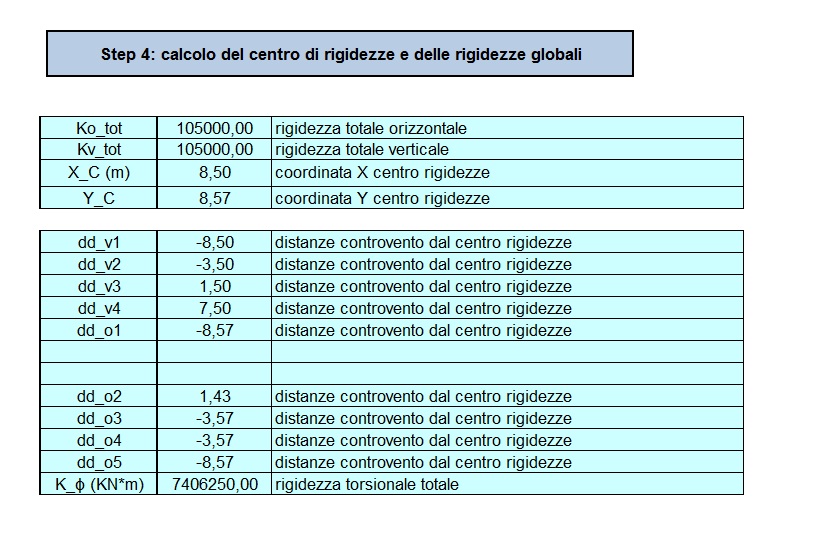
Individueremo quindi il centro di massa e il centro di rigidezza dell'intero impalcato

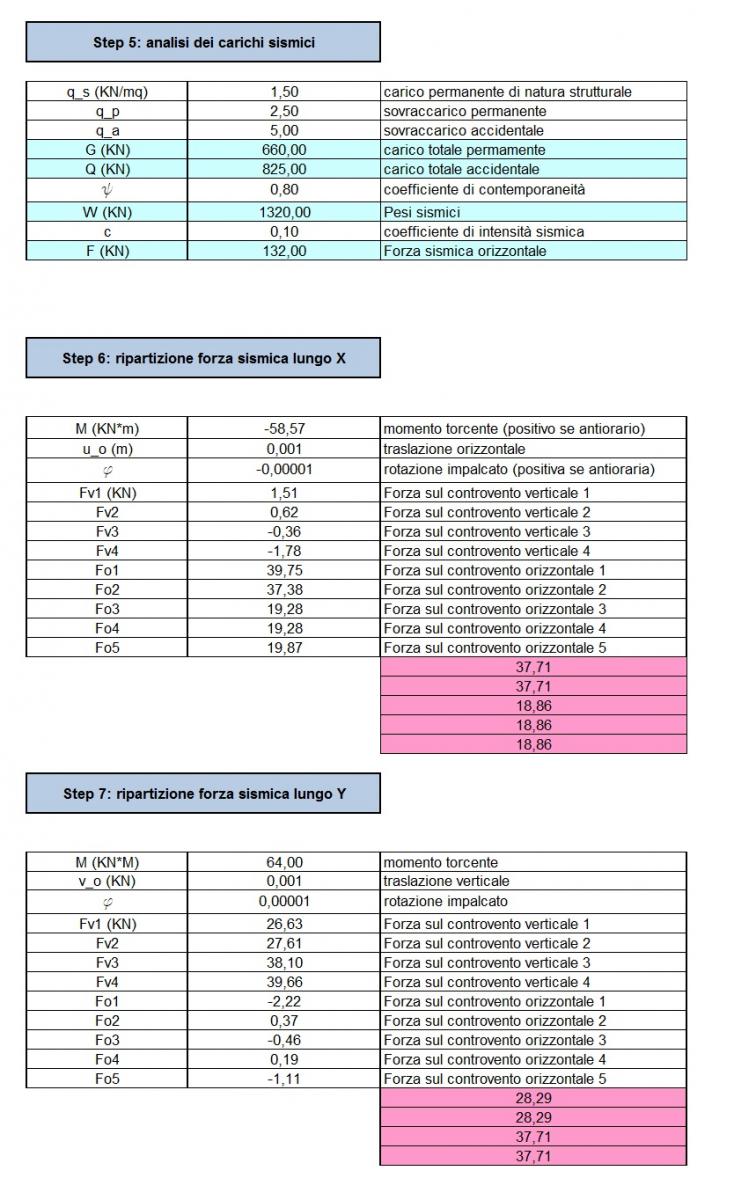
5| Scegliamo quindi un tipo di pacchetto per il solaio, in modo da definire i carichi strutturali, permanenti ed accidentali che vi agiscono. Dalla somma dei carichi strutturali, permanenti e accidentali della struttura (qs, qp e qa), calcoleremo i carichi sismici che verrano ripartiti lungo gli assi X e Y per ogni controvento.

MODELLAZIONE SU SAP

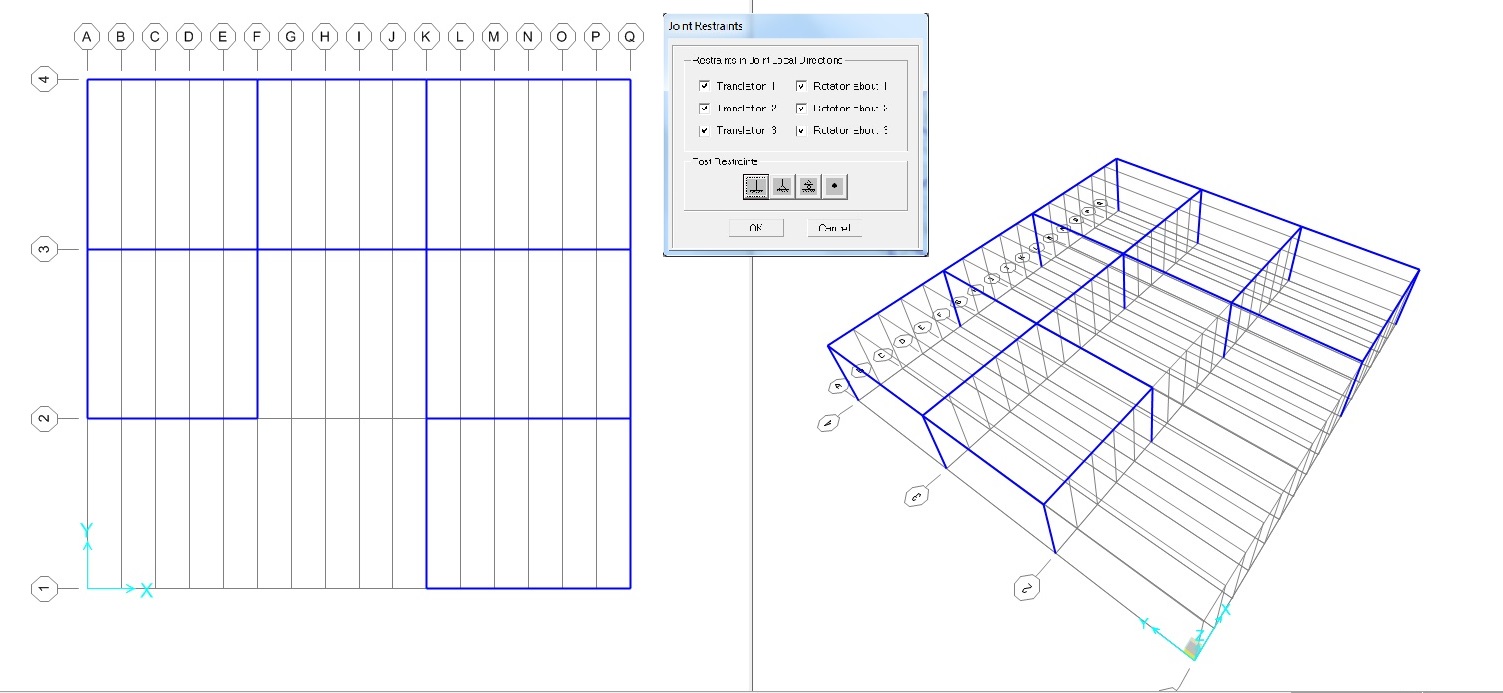
Come nelle precedenti esercitazioni, analizzeremo il nostro sistema sul software SAP. Il primo passaggio è quello di ridisegnare l’impalcato, assegnando come vincolo alla base dei pilastri degli incastri.

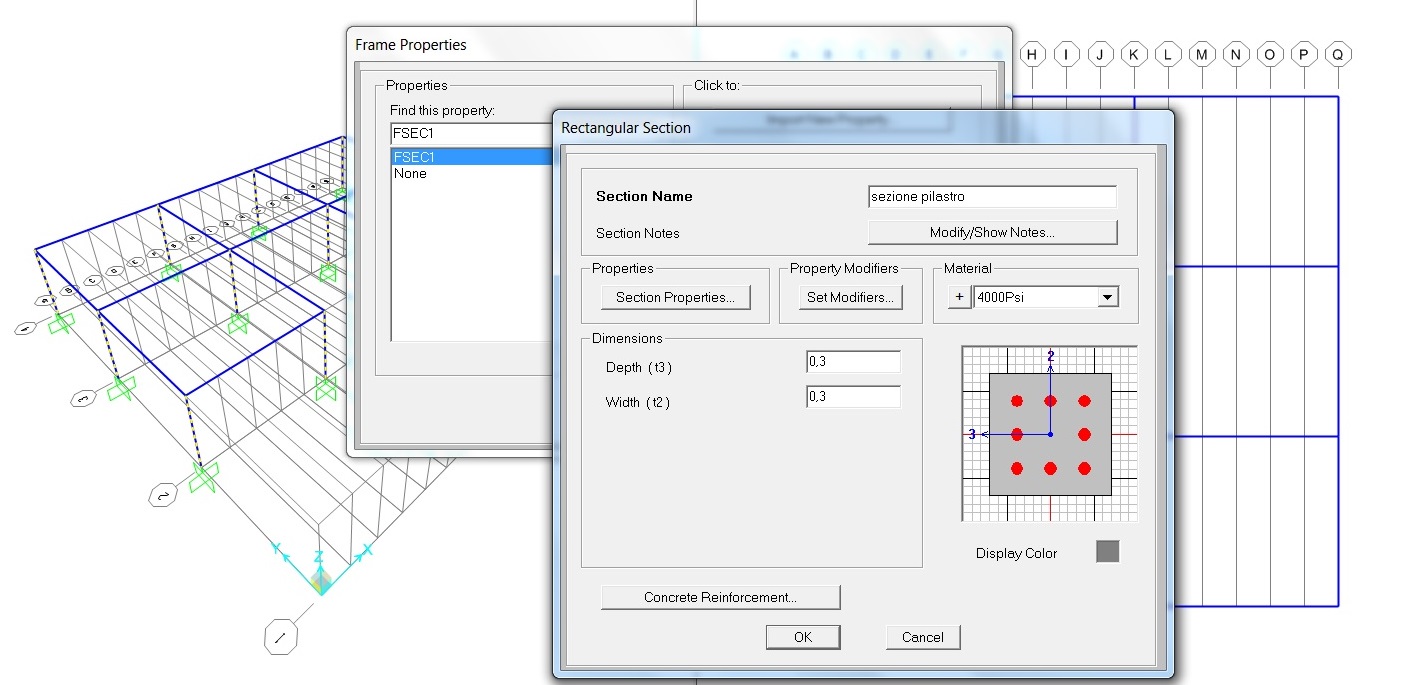
Procediamo adesso con la definizione della sezione dei pilastri in cemento armato, definendo una sezione di dimensioni 30 cm x 30 cm e delle travi di dimensioni 30 cm x 60 cm.

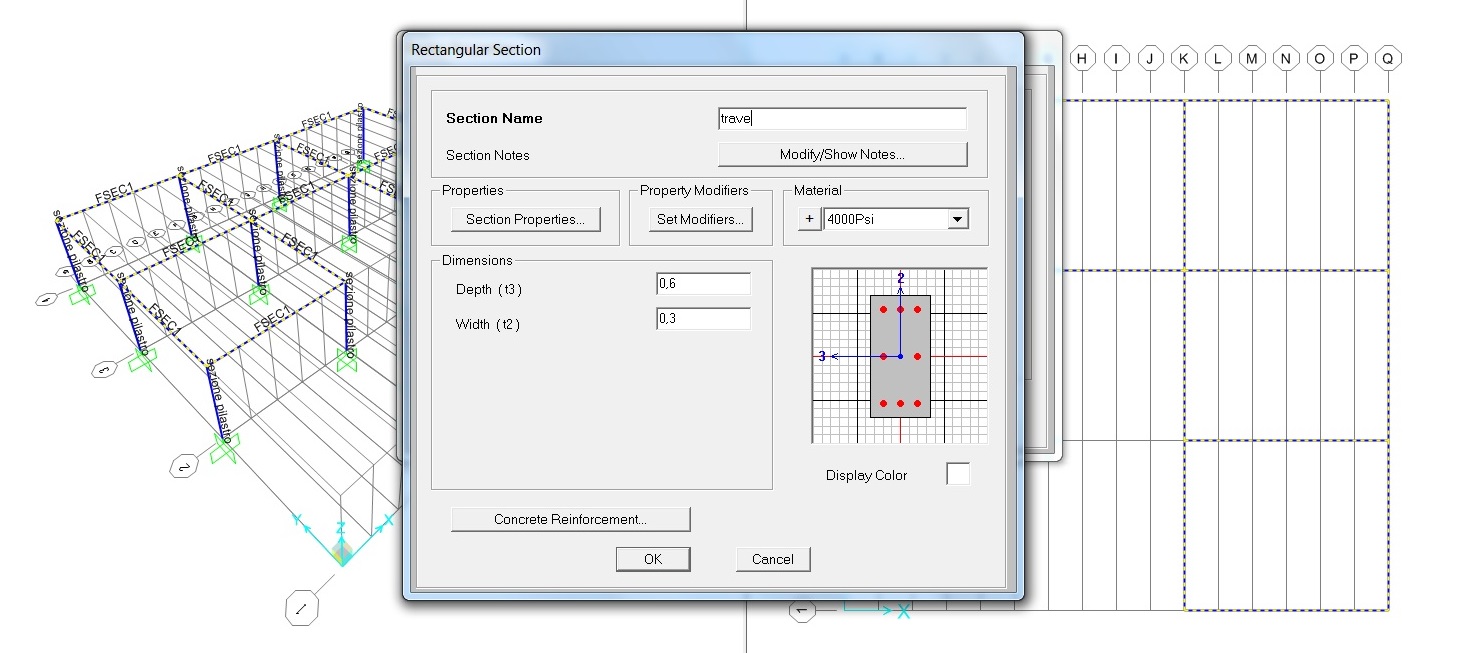
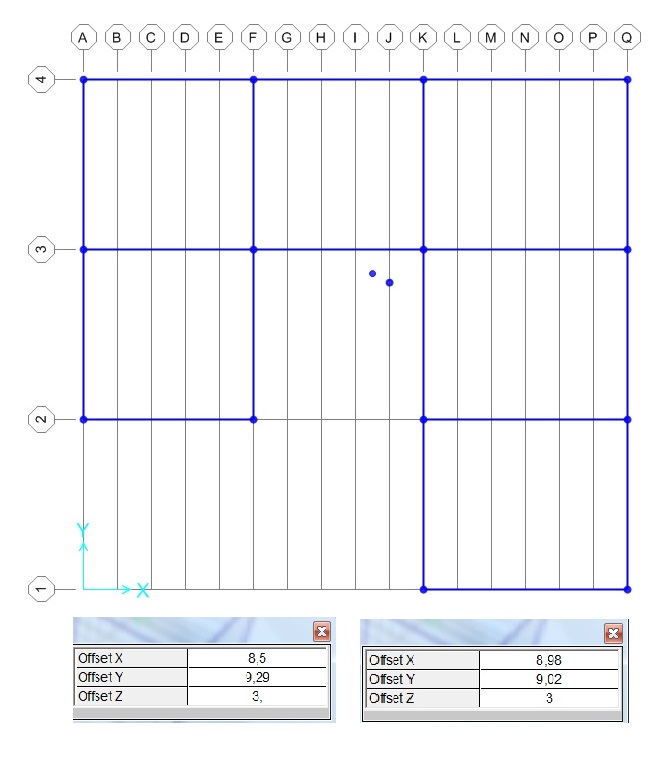
Riportiamo ora la posizione del centro di massa e del centro di rigidezza con i dati precedentemente trovati con il calcolo del foglio excel. 

[!] per disegnare un punto su SAP, basta cliccare sull’icona che raffigura un punto, in alto a ssinistra dello schermo. Si aprirà una piccola finestra dove possiamo inserire le coordinate del punto rispetto all’origine, una volta inseriti i dati cliccare sull’origine del sistema destroso e chiudere la finestra.

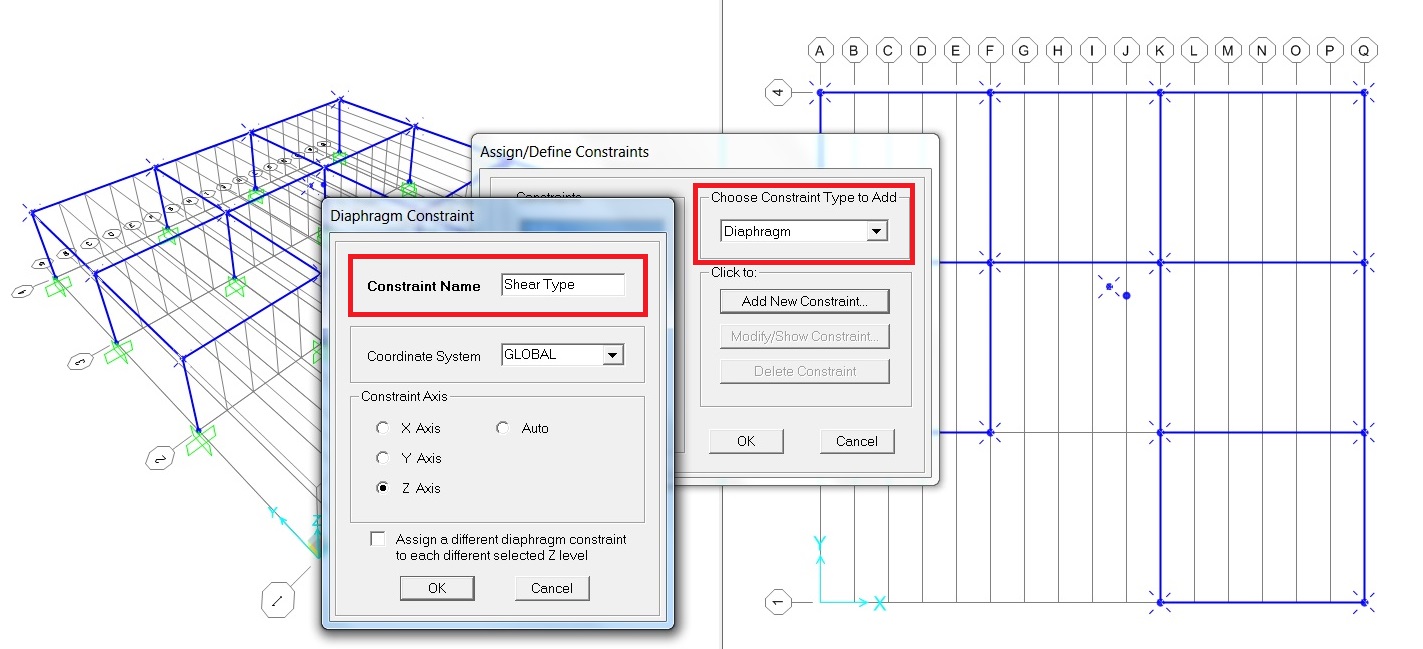
Ora dobbiamo rendere rigida la struttura, quindi andremo a selezionare tutti i nodi (trave/pilastro) ed il centro delle rigidezze. Poi clicchiamo ’Assign’>’Joint’>’Costrains’. Si aprirà una finestra , ‘Assign/Define Costrains’ e a sinistra sul menù a tendina selezionare la voce ‘Diaphragm’. Infine su ‘OK’

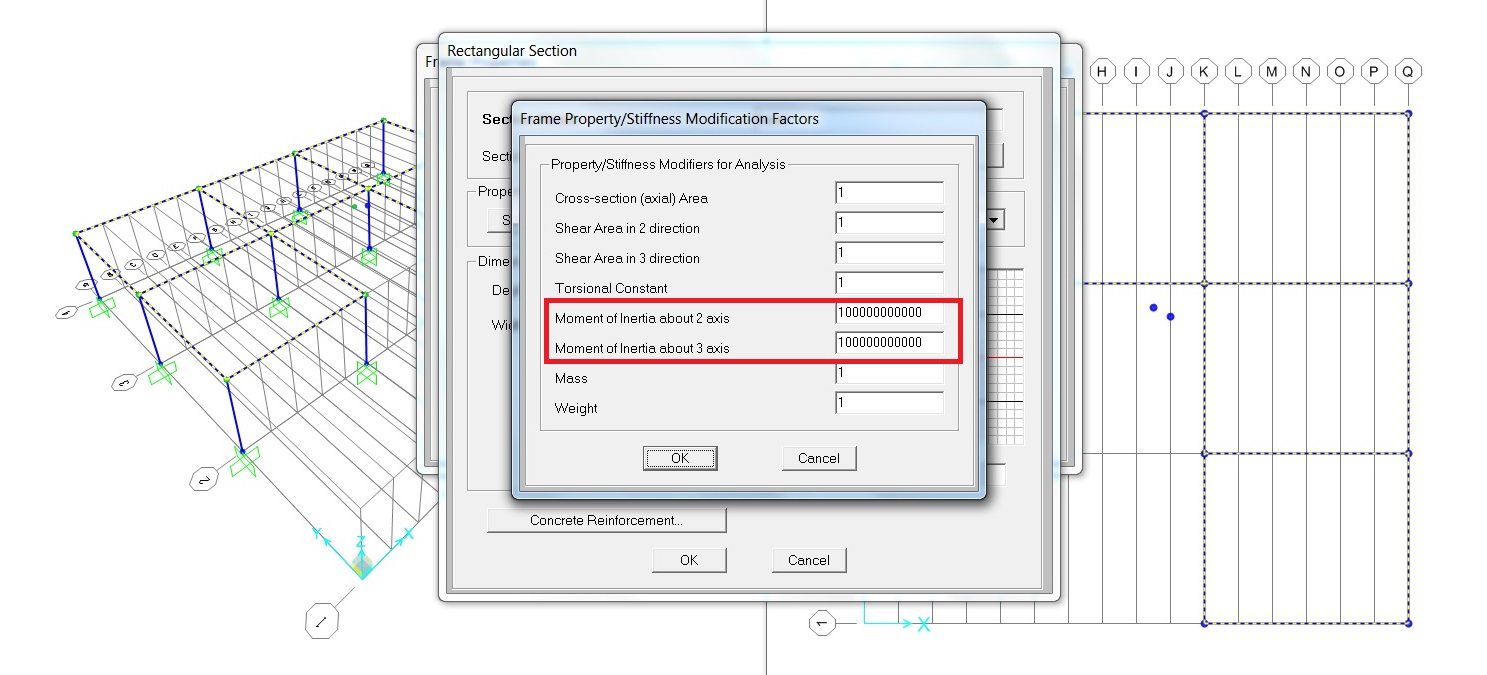
Dal momento che stiamo utilizzando un telaio shear type, renderemo indeformabili le travi: per farlo possiamo decidere di aumentare considerevolmente il momento di inerzia, andando su ‘Assign’>’Frame’>’Frame Sections’.

Si aprirà una finestra, ‘Frame Properties’, selezioniamo la nostra sezione delle travi e quindi su ‘Modify/Show Property’, si aprirà un’altra finestra, ‘I/Wide Flange Section’. Cliccare su ‘Set Modifiers’.

Nell’ultima finestra che si apre, ‘Frame Property/Stiffess Modification Factors’, andiamo ad aumentare la voce ‘Moment of Inertia about 2 axis’. Infine su ‘OK’. 

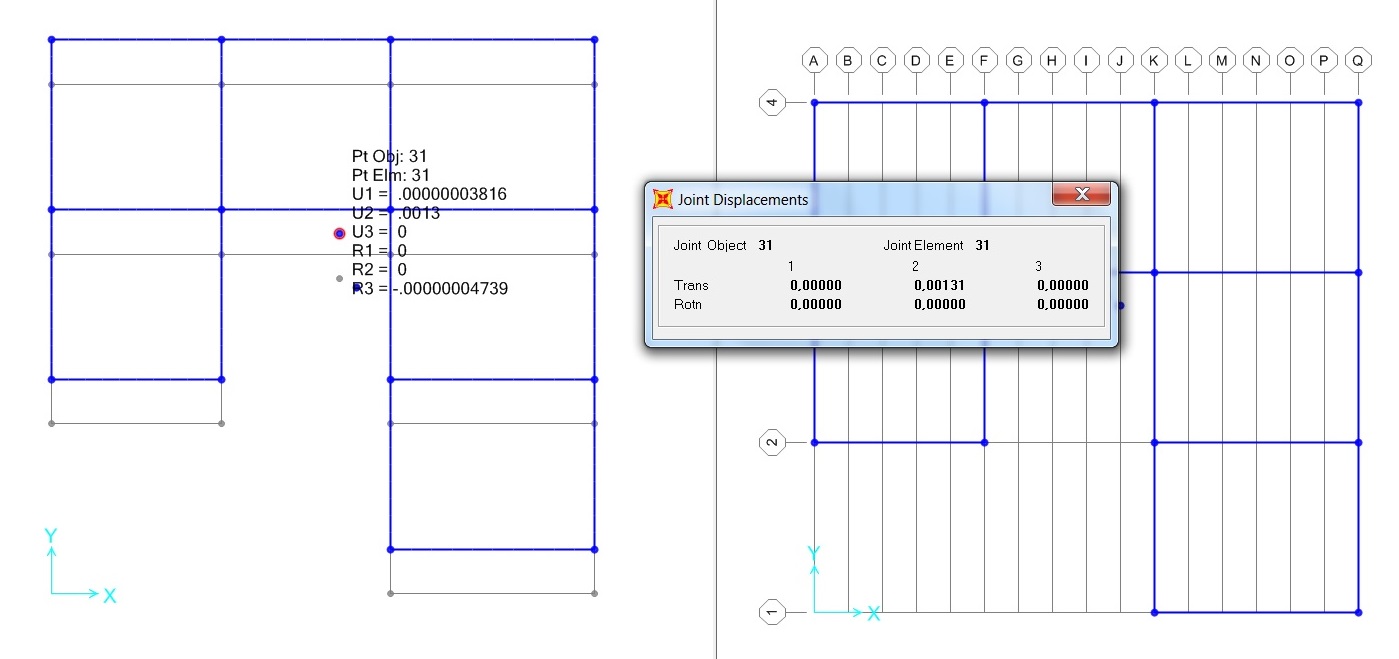
Possiamo adesso assegnare una forza puntuale applicata al centro delle rigidezze, in direzione Y pari alla ‘Forza Sismica Orizzontale’ trovata in precedenza con il foglio excel (132 KN)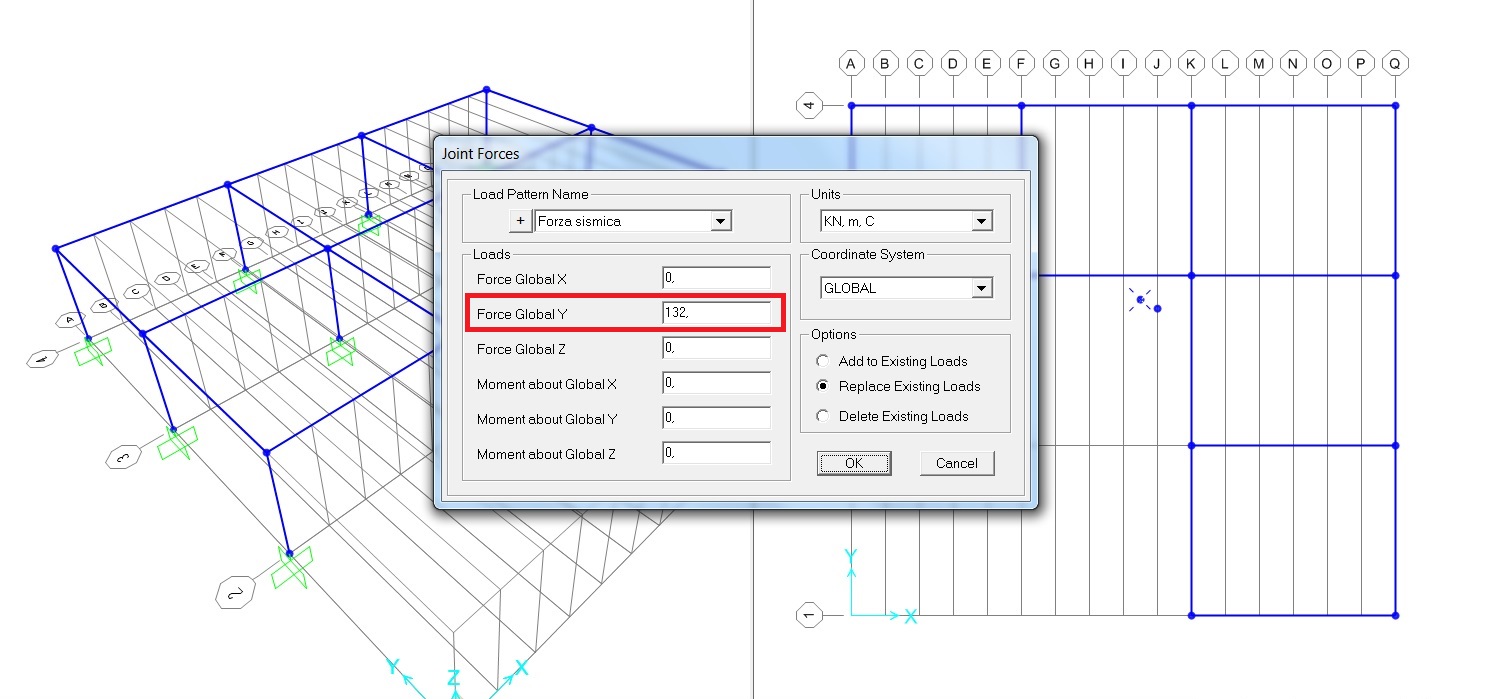

Avviamo l’analisi e vediamo come si comporta l’impalcato.  Come previsto, la deformata mostra una traslazione rigida lungo l’asse y dell’impalcato (la rotazione è praticamente irrisoria).