Esercitazione 4_ Centro delle rigidezze

La quarta esercitazione riguardo lo studio della ripartizione di una sollecitazione orizzontale, o forza sismica.

Per resistere a spinte di questo genere, l’edificio ha bisogno di controventi.

Un telaio Shear Type funziona bene come controvento e per questo abbiamo deciso di utilizzarlo in questa esercitazione.

Studiamo una struttura di un piano in cemento armato.

Avendo  un telaio Shear-Type, la rigidezza del singolo pilastro sarà pari a K=12EJ/12.

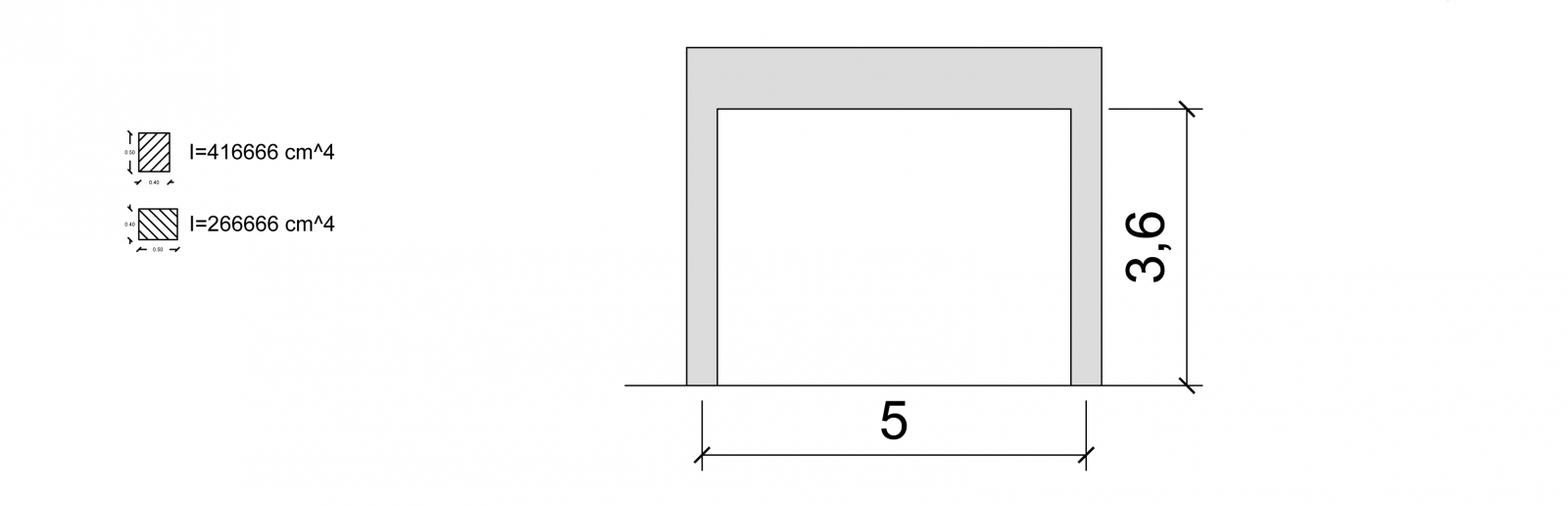
Il momenti di inerzia, I=b*h^3/12 per le sezioni rettangolari, cambierà a seconda del verso in cui è collocato il pilastro:

• con b= 40 cm e h=50 cm avremo Ix=416 666, 66 cm^4
• con b=50 cm e h=40 cm avremo Ix=266 666,66 cm^4

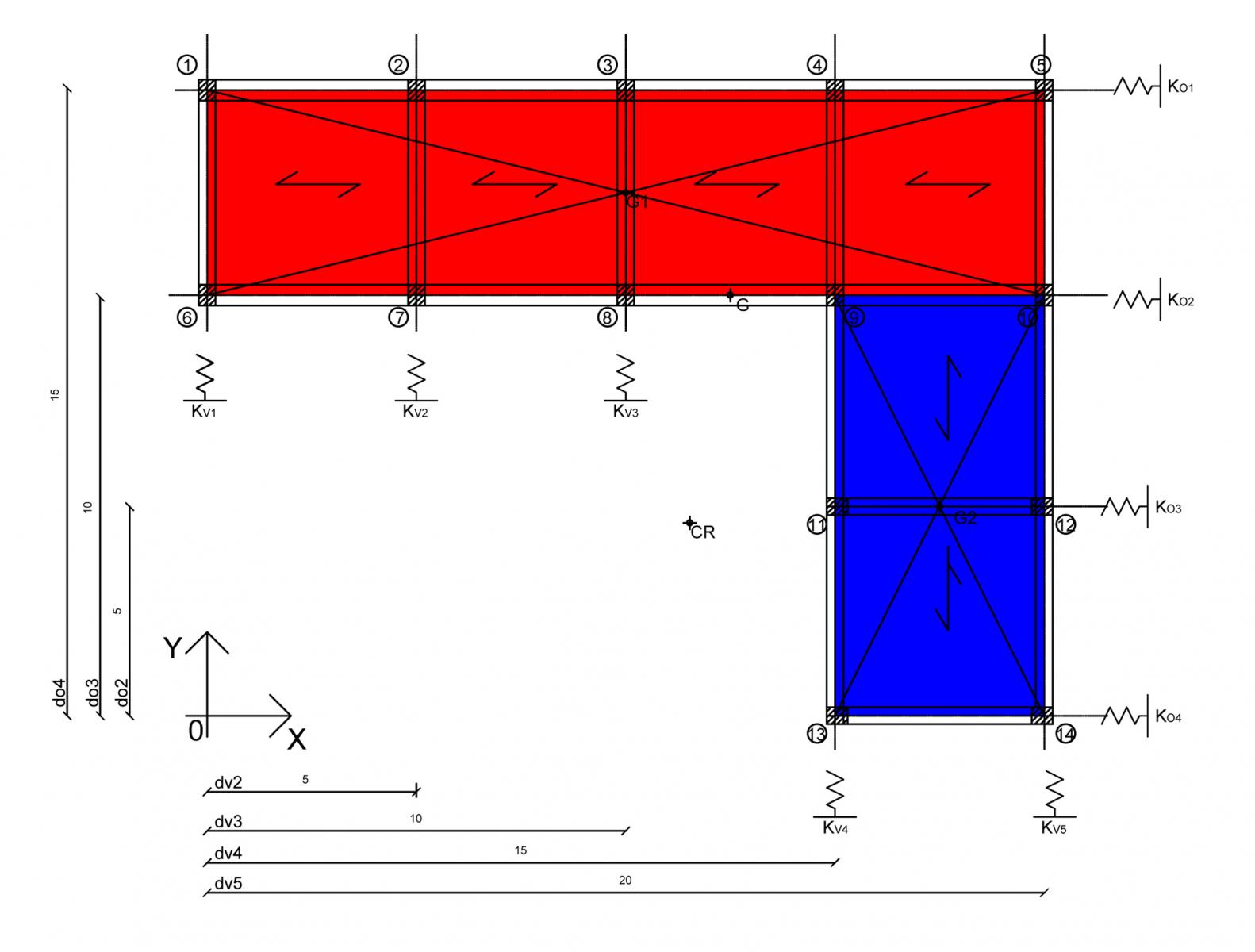
Iniziamo con il calcolo delle rigidezze traslanti dei controventi dell’edificio.

Andranno inseriti:

- i pilastri, numerati in precedenza per essere riconosciuti;

- E, il modulo di elasticità del materiale, in questo caso cls, quindi E=21000 N/mmq;

- H, altezza del pilastro

- I, momento di inerzia di ogni singolo pilastro

Fino ad ottere Kv, o Ko, per individuare la rigidezza complessiva del telaio.

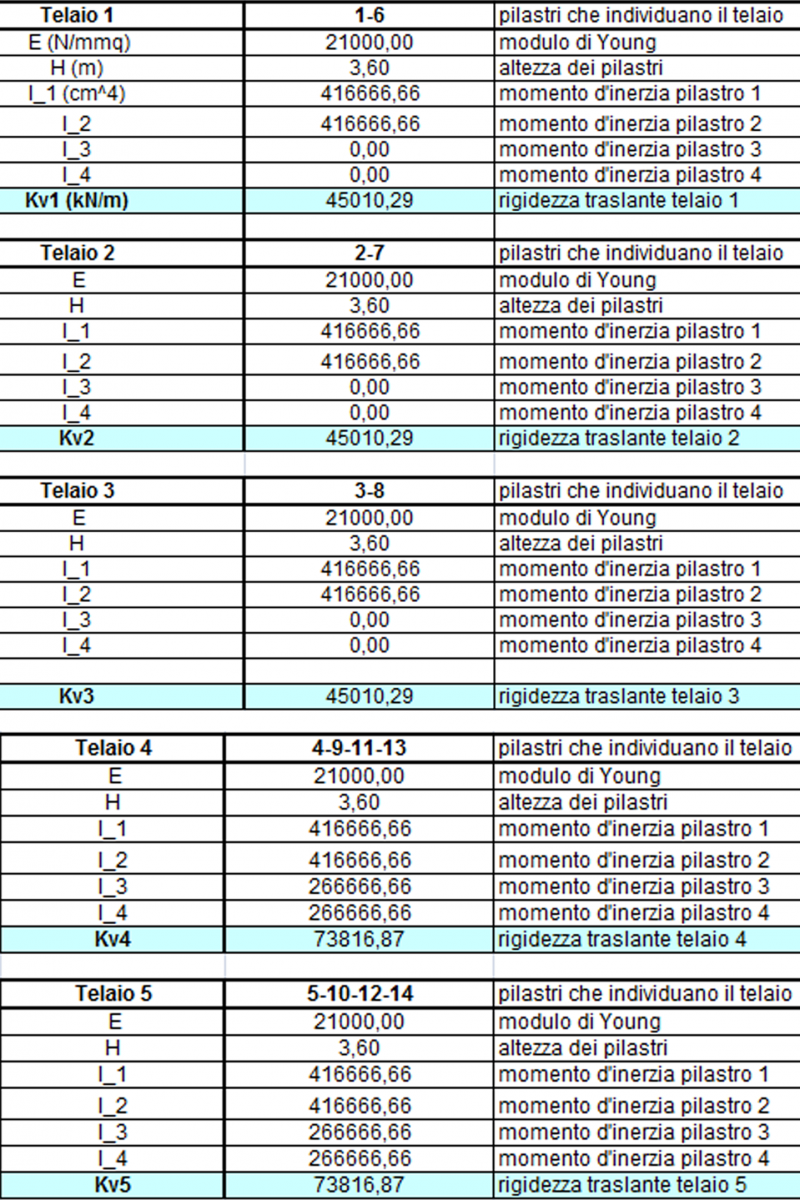
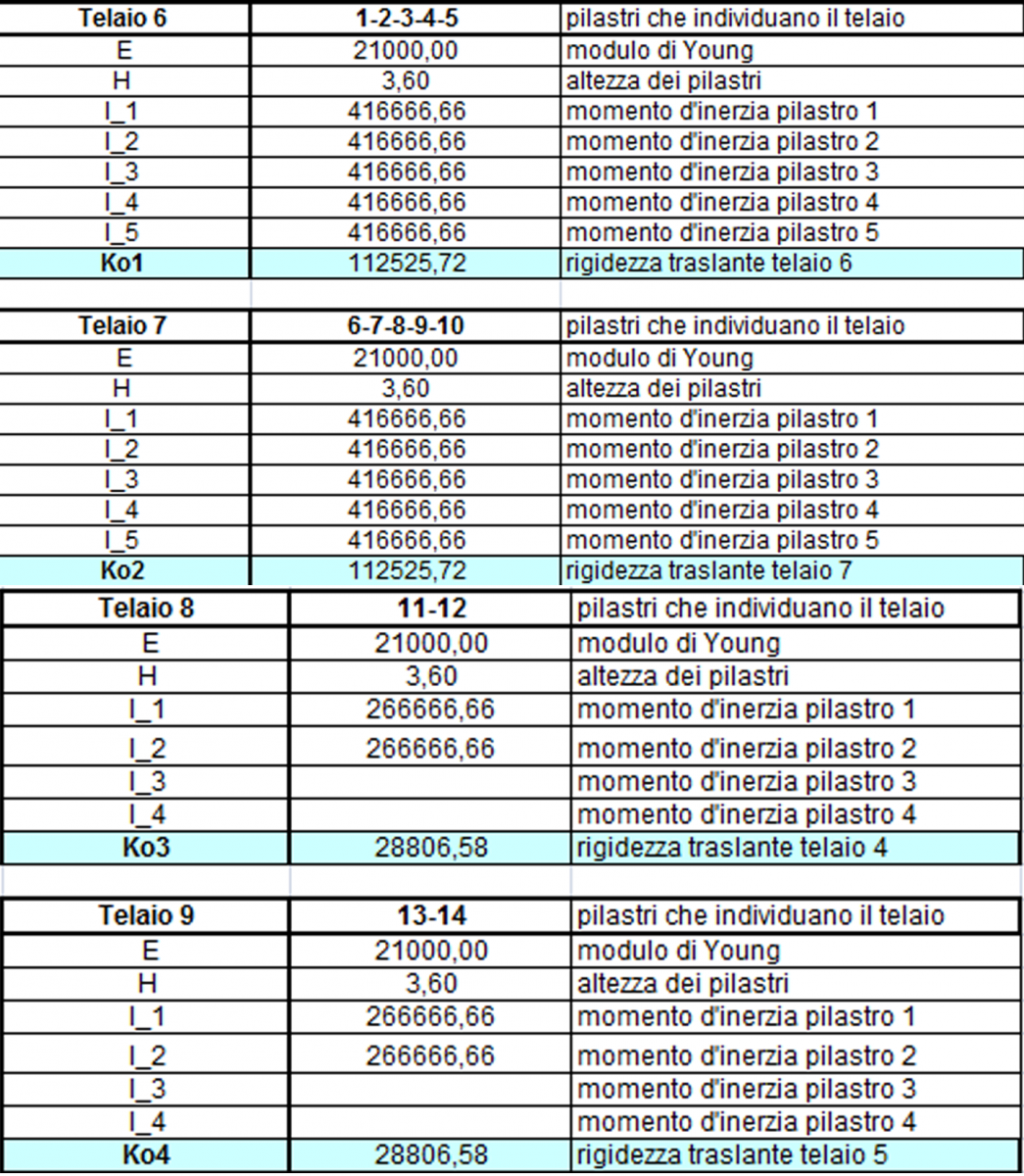
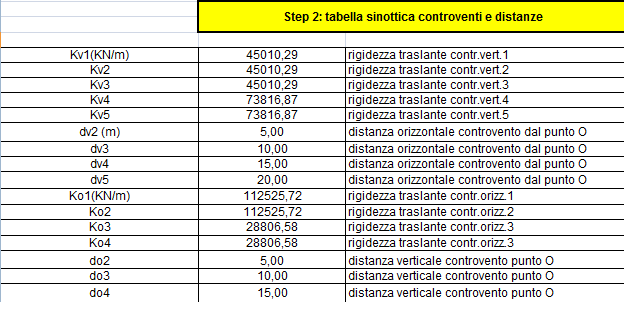
Il secondo passaggio riassume i valori trovati nelle tabelle superiori e incorpora le distanze di questi telai da un punto 0 indicato. Servirà per calcolare il centro di massa della struttura.

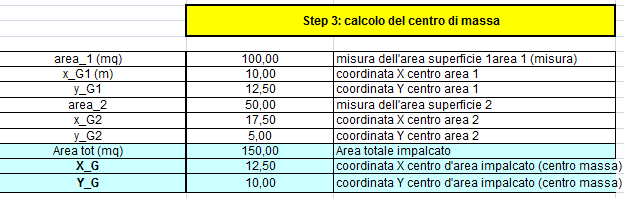
Il terzo passo è il calcolo del baricentro della struttura. Troveremo le coordinate di G: (X_G; Y_G)

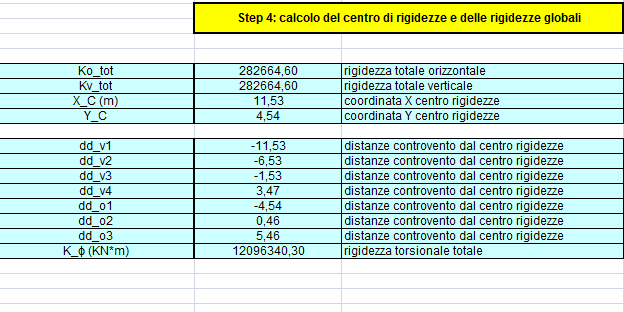
Il quarto passo riguarda il centro delle rigidezze C: (X_C; Y_C) e il calcolo del valore della rigidezza torsionale totale

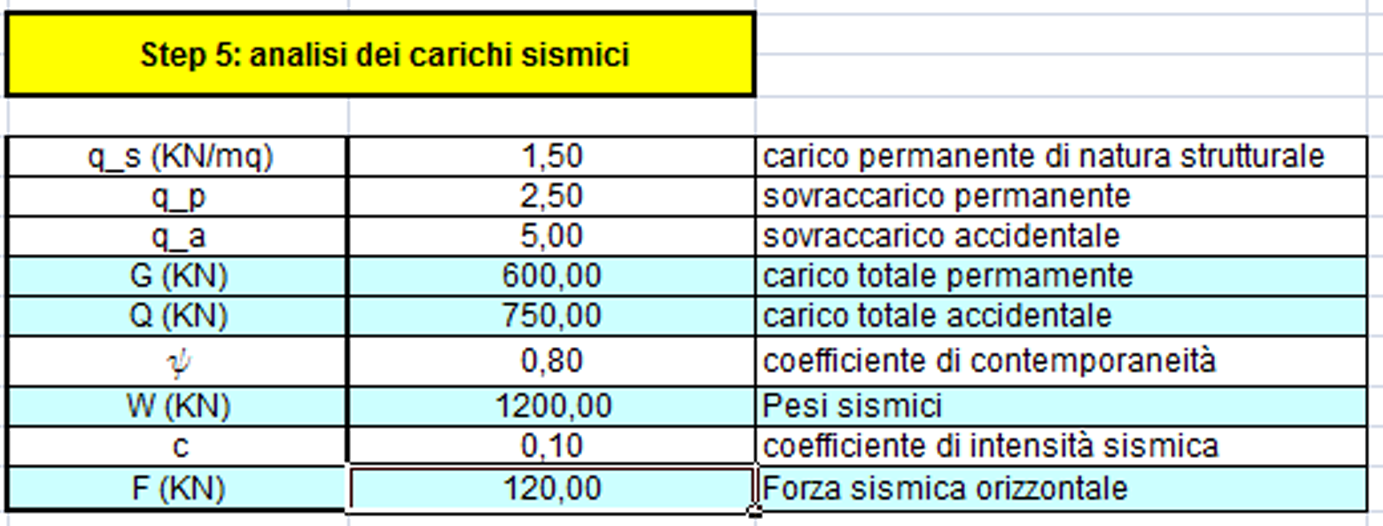
Il quinto passo è un calcolo che riguarda l’analisi dei carichi sisimici totali: studio dei carichi fino ad ottenere W, ovvero il totale dei pesi sismici, che moltiplicato per il coefficiente di intensità sismica ci da la F, la forza sismica orizzontale.

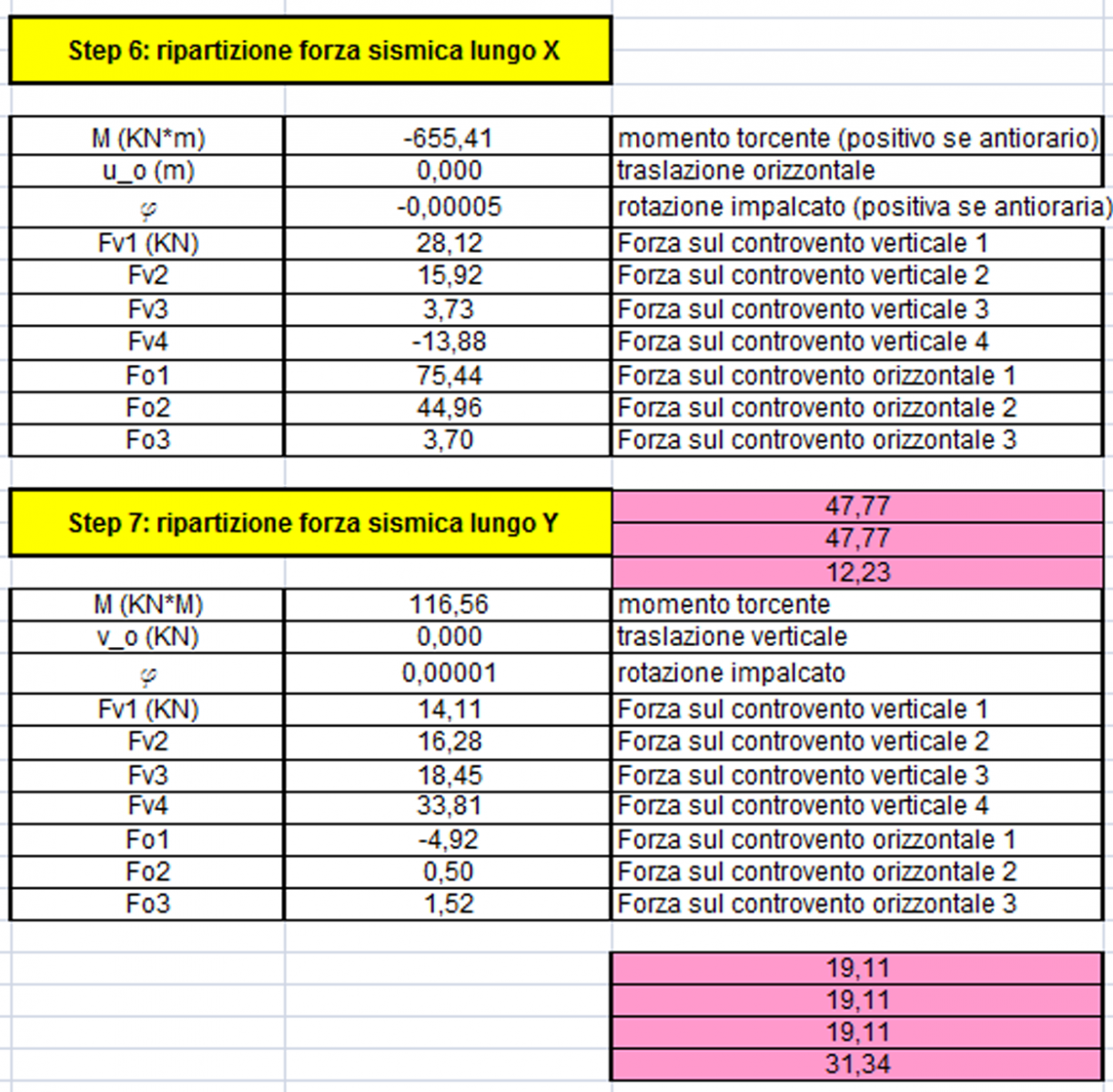
Il passo 6 e 7 studiano F sismica nelle componenti orizzontali e verticali.

I pilastri presi in esame sono sottoposti ad una momento torcente pari a:

M torcente lungo X = F *(X_C-X_G)

M torcente lungo Y = F *(Y_C-Y_G)

Il braccio è la distanza tra centro delle rigidezze e centro di massa, individuato in X o in Y a secondo del momente torcente studiato.

I pilastri non traslano nell’estremità inferiore in quanto hanno un incastro alla basa, ma lo fanno superiormente.

La forza sismica è assorbita dalle rigidezze del telaio.

Avremo che la traslazione verticale è data da:

v_o=Fsismica/Kv_tot

Mentre quella orizzontale è data da:

u_o=Fsismica/Ko_tot

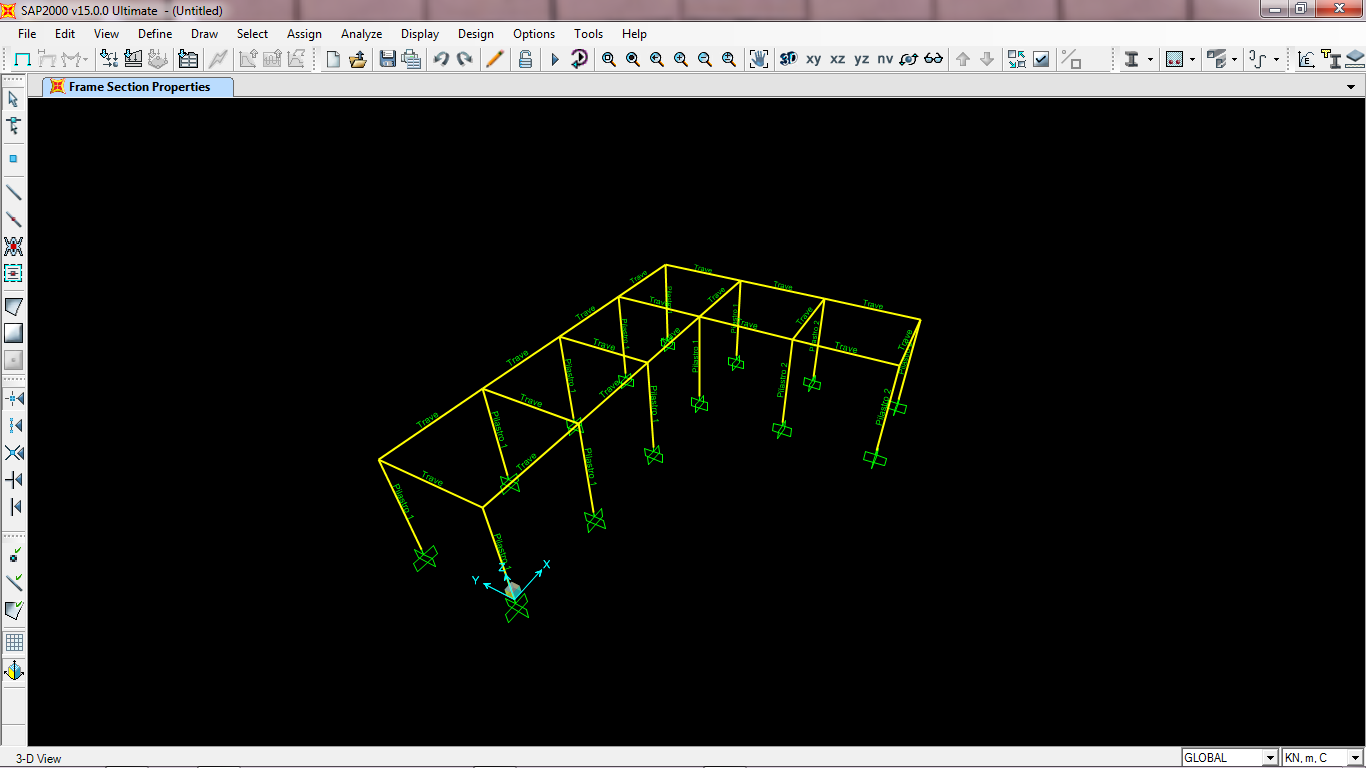
Importiamo la struttura su Sap, impostiamo gli incastri alla base dei pilastri.

Per ipotesi del telaio Shear Type sappiamo che le travi di questo sono infinitamente rigide, quindi, nel materiale, andiamo a modificare E rendendolo molto grande.

Andiamo anche a definire le sezioni dei pilastri, in quanto una tipologia avrà 30x40 cm, mentre un’altra ne avrà 40x30 cm.

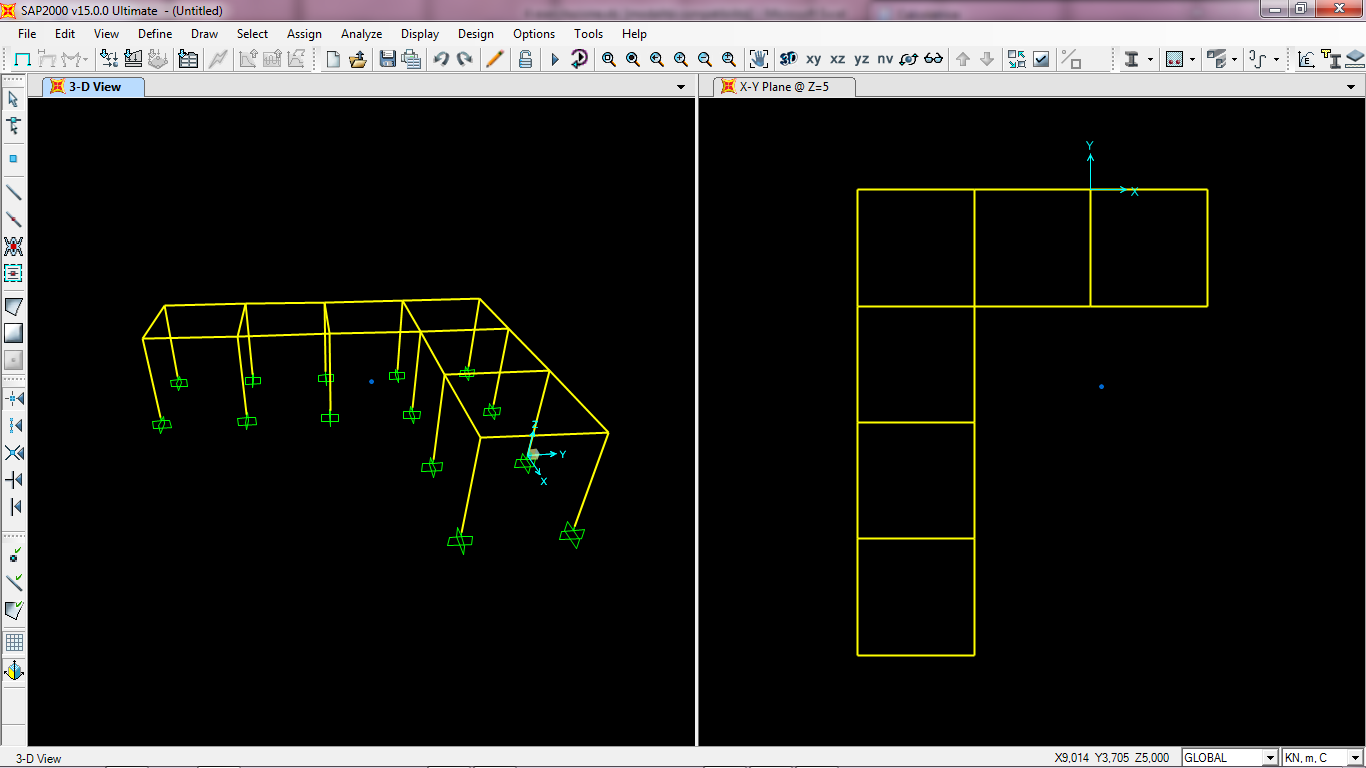
Colloco il centro delle rigidezze con coordinate C (11,53, 4,54), con il nuovo centro di riferimento del piano cartesiano saranno CR (0,46, -8,47).

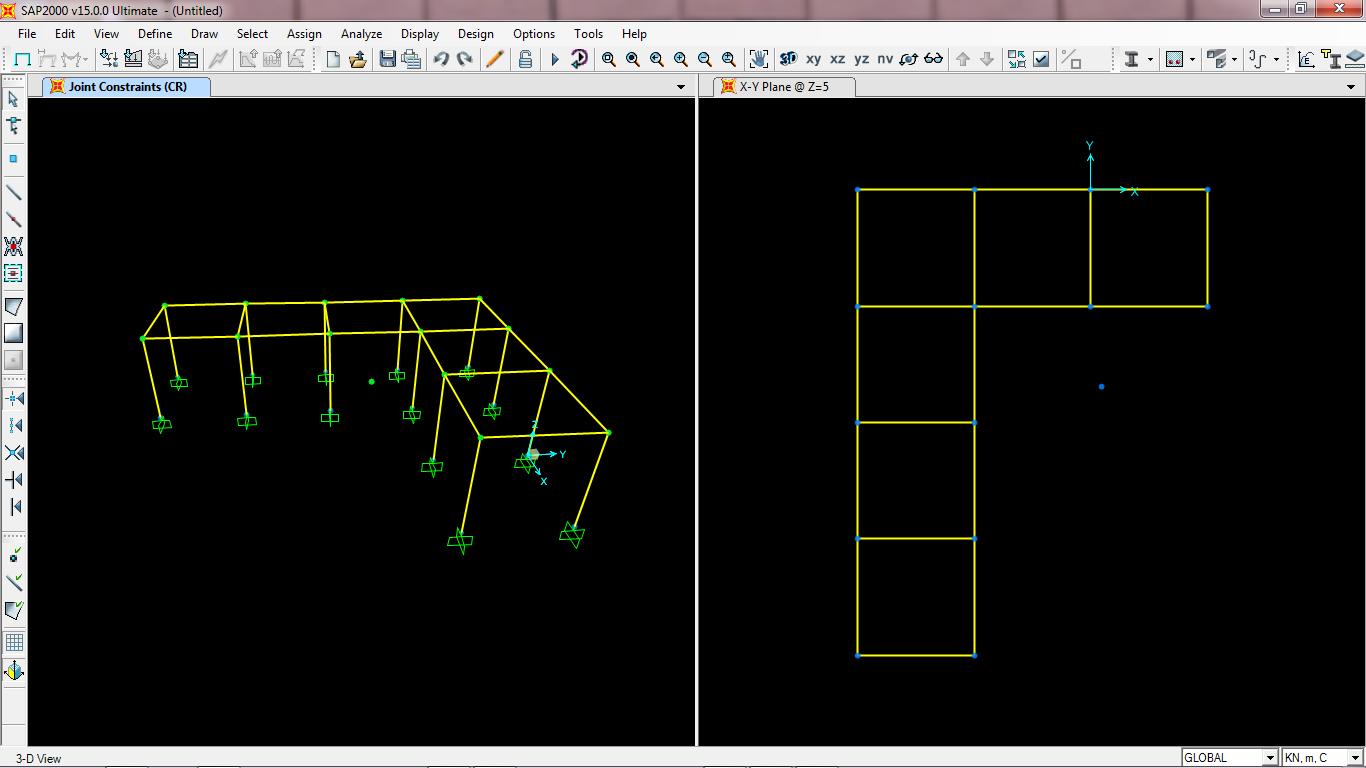
Imposto il comando Diaphragm, in modo che tutti i nodi del telaio siano collegati al CR.

Applico una forza orizzontale lungo l’asse X F=120 kN

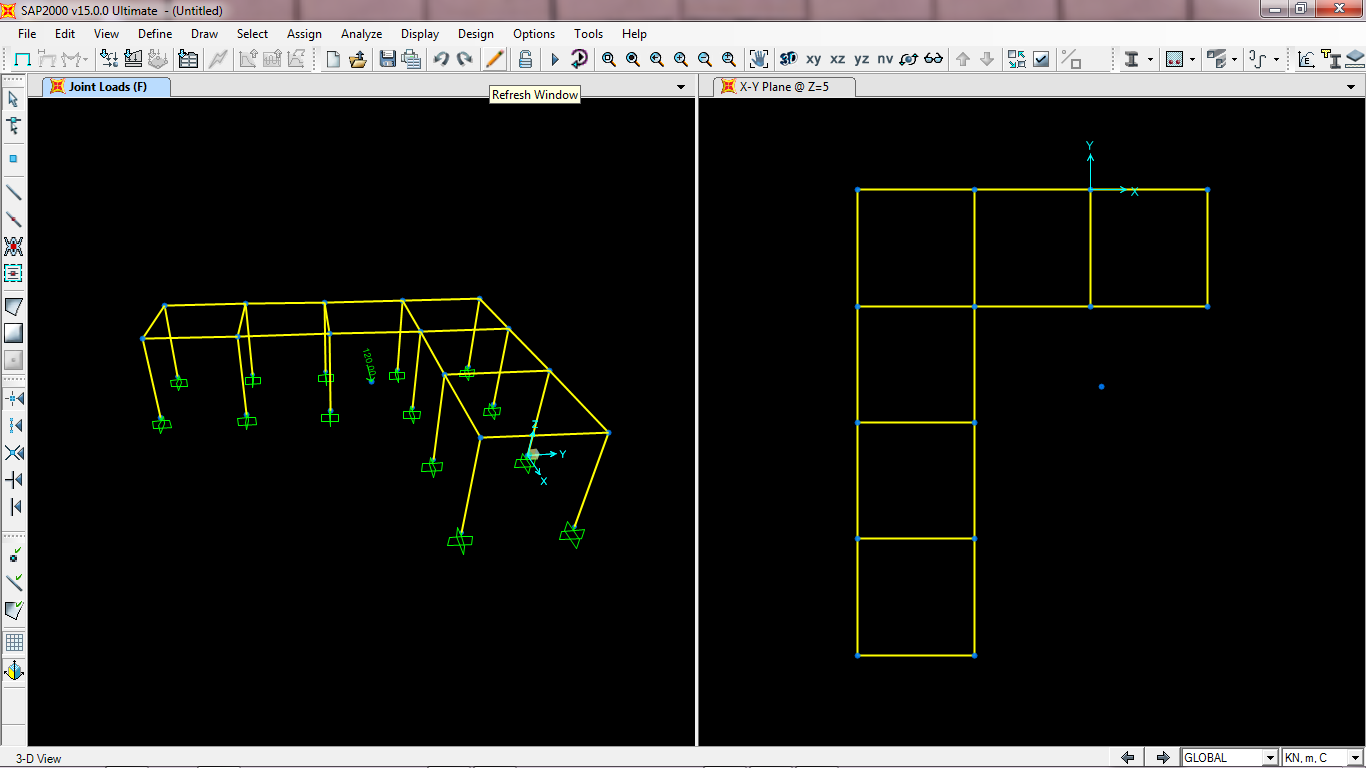
Clicco sul comando Run, facendo “correre” solo F=120 kN

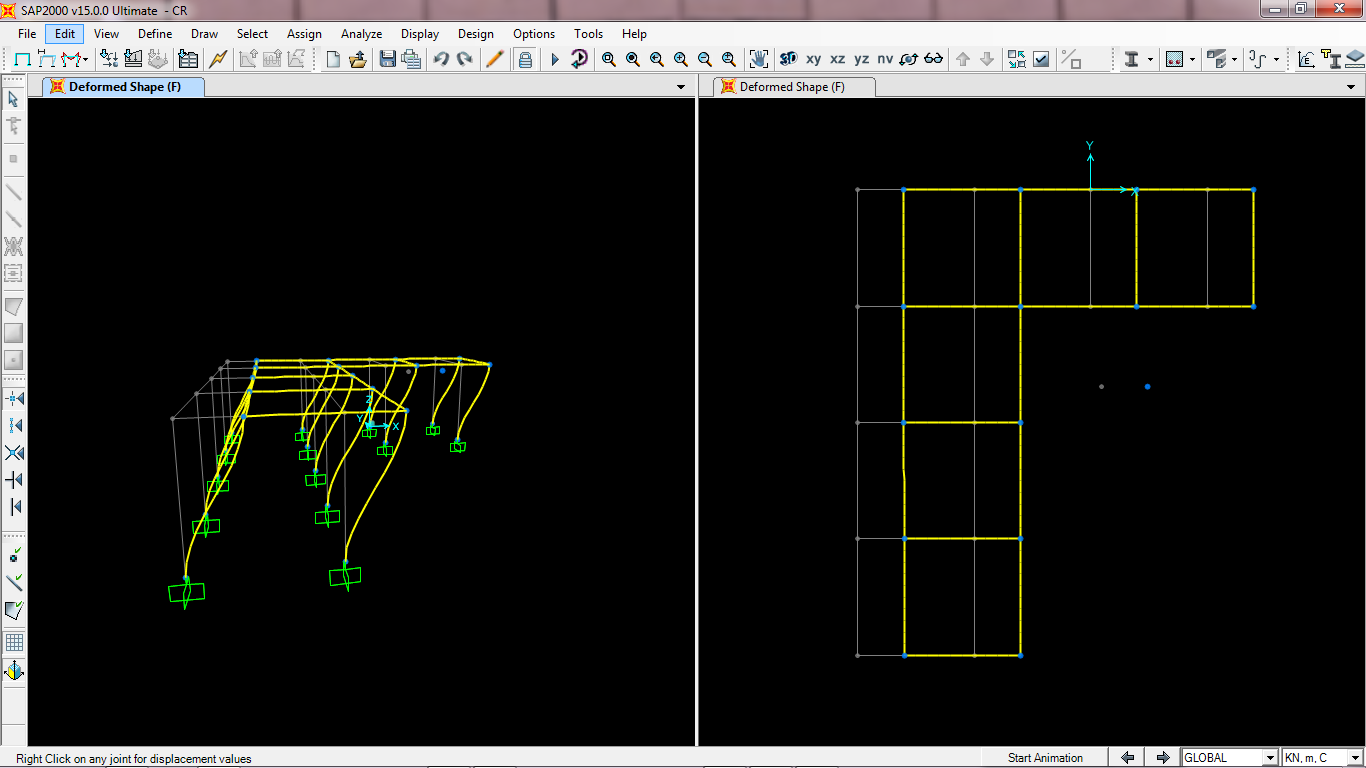
Il telaio trasla lungo X senza ruotare e il pilastri si deformano ad “S”.

I calcoli eseguiti su Excel sono verificati!