ES 1a - Reticolare 2D
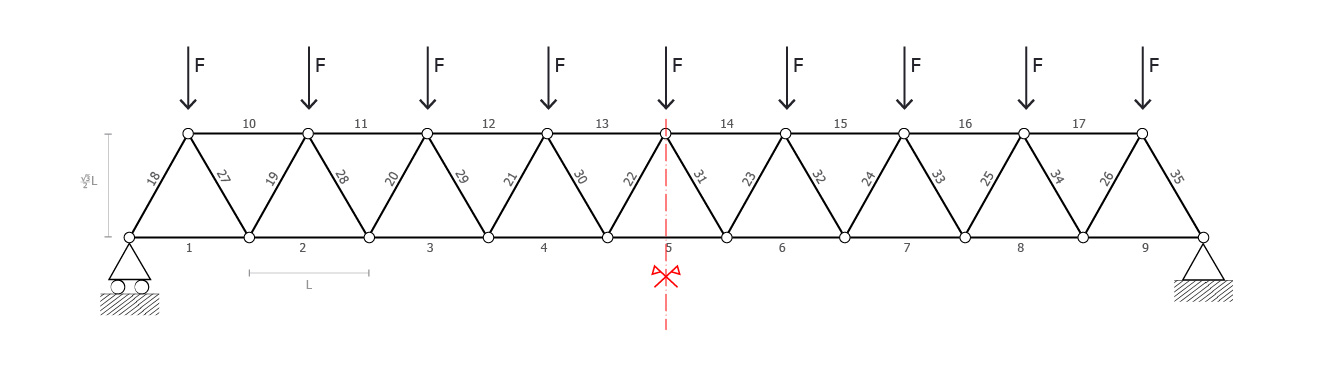
Mi appresto a risolvere questa reticolare piana. Si tratta di una struttura composta da triangoli equilateri. Così composta oltretutto, la struttura può essere considerata simmetrica, ecco perché posso permettermi di concentrarmi su una delle due parti della struttura, al suo simmetrico il comportamento sarà appunto, simmetrico.
Prima procederò con il Metodo delle Sezioni di Ritter (1) e in seconda battuta con il programma SAP2000 (2).
(1) Metodo delle Sezioni di Ritter
In questa fase farò un'analisi cercando di trovare quali siano le parti più sollecitate della struttura e quindi le aste poste a maggior sforzo (siano esse tiranti o puntoni), le quali immagino già siano in corrispondenza del modulo centrale. Posso ricavarmi le reazioni vincolari R=9/2 F

Il metodo, in sostanza, taglia tre aste. Ognuna delle aste ha un suo sforzo normale che vado a rappresentare uscente da essa (con verso completamente casuale, NDR).
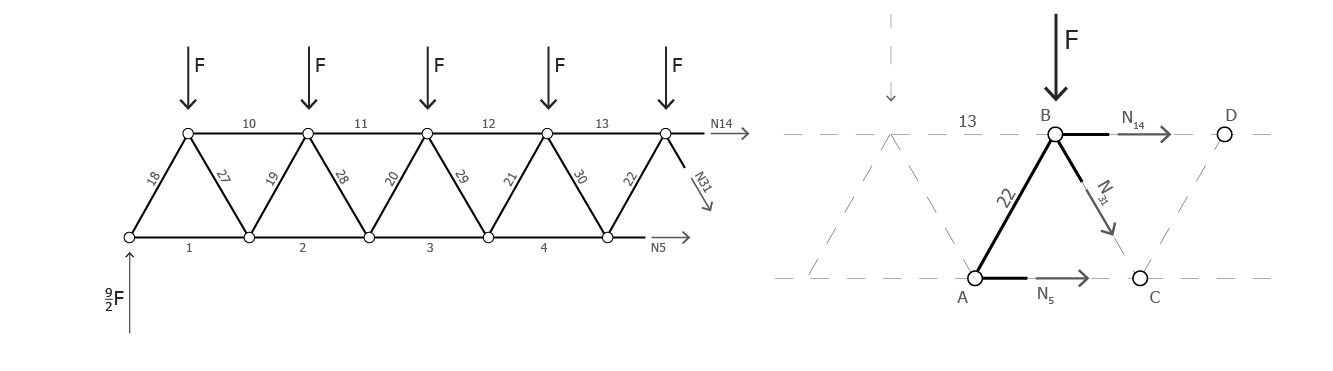
Procedo considerando l'equilibrio a rotazione per i nodi C e D
NODO C Mc=0 ⇒ -N14(3½/2)L+F(L/2)+F(3L/2)+F(5L/2)+F(7L/2)+F(9L/2)-(9F/2)5L=0 ⇒ N14=(-20*3½*F)/3
Il valore dello sforzo normale dell'asta 14 è negativo, siamo quindi in presenza di un'asta compressa, ovvero di un puntone. [Attenzione! Il verso di N14 così disegnato è sbagliato, si tratterebbe dell'opposto in quanto negativo] Allo stesso modo tutte le aste superiori della struttura saranno dei puntoni. L'intensità di N diminuirà all'avvicinarsi verso il vincolo in quanto sempre meno forze agiscono sulla parte di struttura presa in considerazione. Per esempio: N10=(-8*3½*F)/3 NODO D MD=0 ⇒ N5(3½/2)L+FL+F2L+F3L+F4L+F5L-(9F/2)5/2L=0 ⇒ N5=(5*3½*F)/2 Il valore dello sforzo normale dell'asta 1 è positivo, siamo quindi in presenza di un'astra in trazione, ovvero di un tirante. Allo stesso modo tutte le aste superiori della struttura saranno dei tiranti. L'intensità di N diminuirà all'avvicinarsi verso il vincolo in quanto sempre meno forze agiscono sulla parte di struttura presa in considerazione. Per esempio: N1=(13*3½*F)/3Procedo considerando l'equilibrio a traslazione verticale
-5F+9F/2-N31*3½/2=0 ⇒ N31=-(3½*F)/3
Il valore dello sforzo normale dell'asta 31 è positivo, siamo quindi in presenza di un'astra in trazione, ovvero di un tirante.
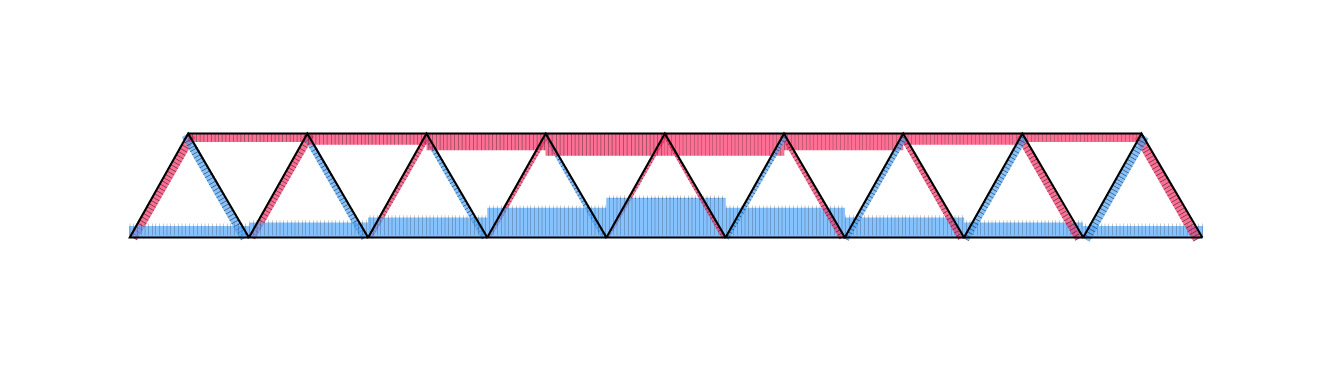
Ecco quindi come si presenta il diagramma dello sforzo normale della struttura, utile per individuare puntoni e tiranti, nonché le aste maggiormente sollecitate.
(2) SAP2000
Cercherò di riprodurre la stessa struttura in SAP2000.
Creando il file nuovo seleziono [2D Trusses] e imposto i valori della reticolare: numero di moduli di base, lunghezza (3 m) e altezza (2,60 m) di questi.
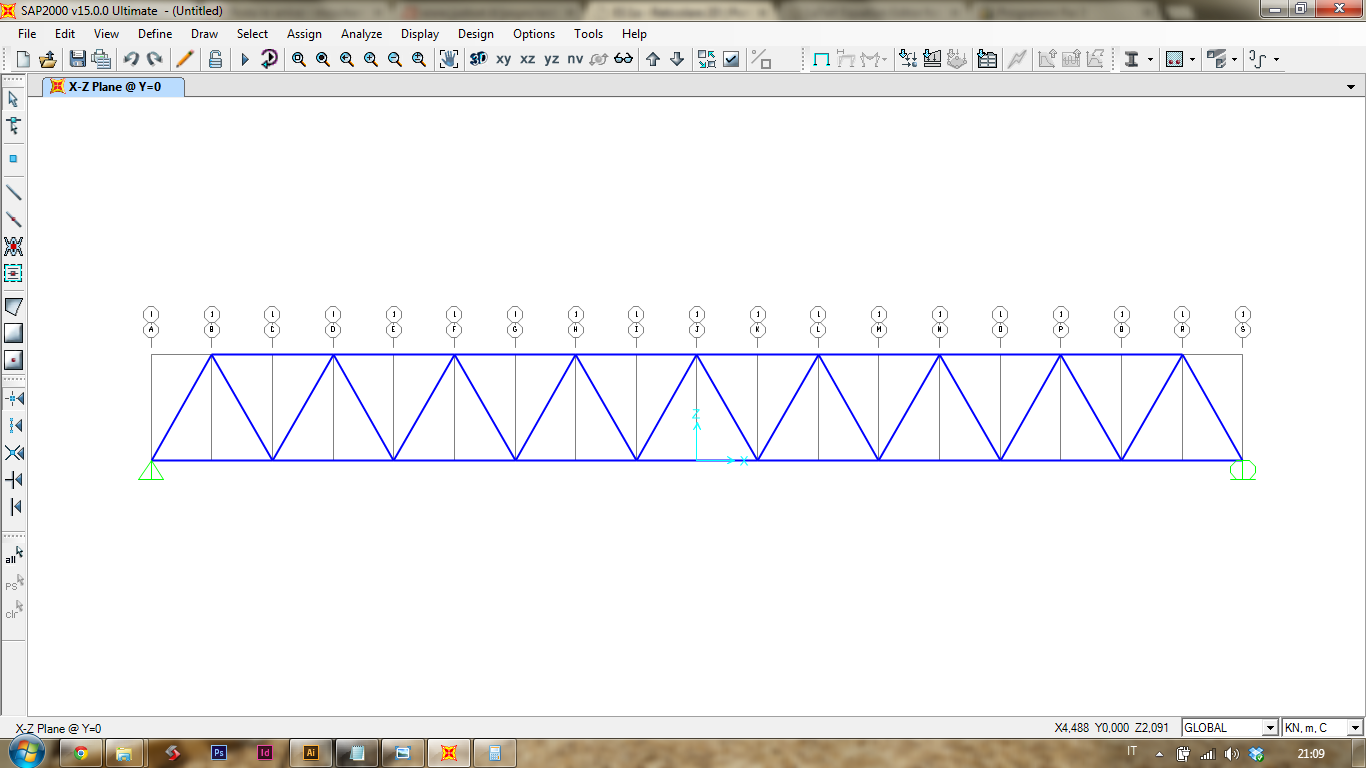
Ed ecco qui la mia struttura.
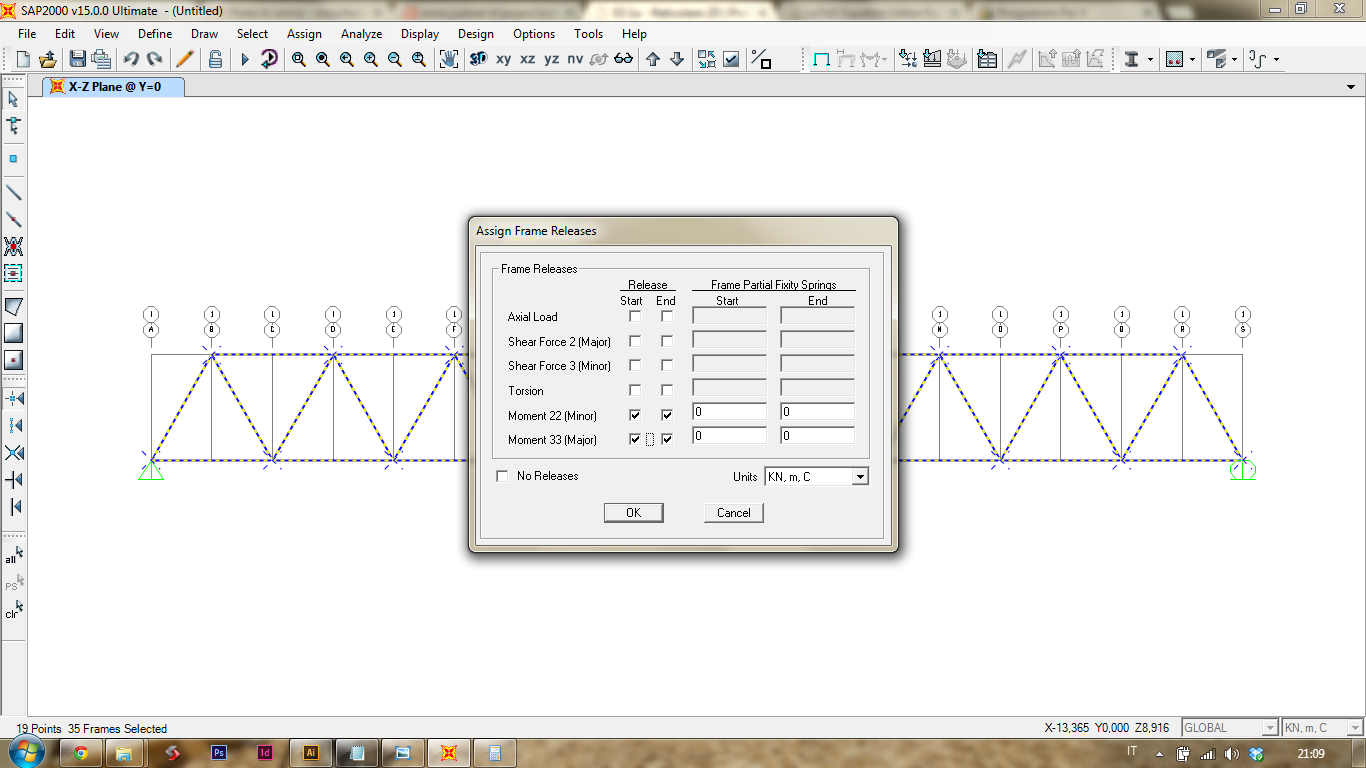
In primo luogo devo "sistemare" alcuni difetti del modello per assicurarmi il corretto funzionamento della struttura.
Impongo che i nodi non trasmettano momento. Selezionando tutta la struttura vado al comando [Assign]>[Frame]>[Release/Partial Fixity]
Selezionando Moment 22 e Moment 33 dando valore 0.
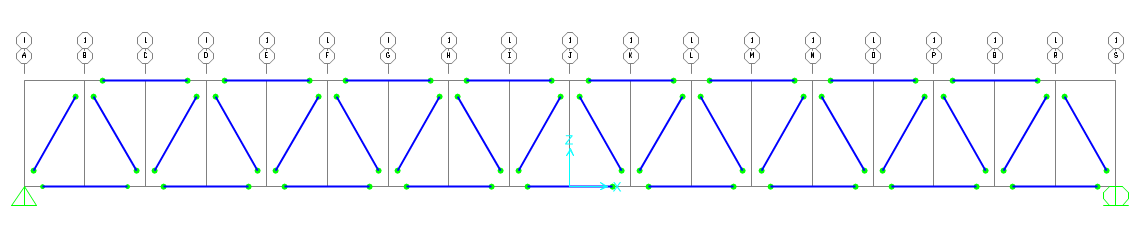
La struttura ora viene visualizzata così.
Imposto ora la sezione delle aste. [Assign]>[Frame]>[Frame Section] e clicco su Add New Property per creare una nuova proprietà disezione.
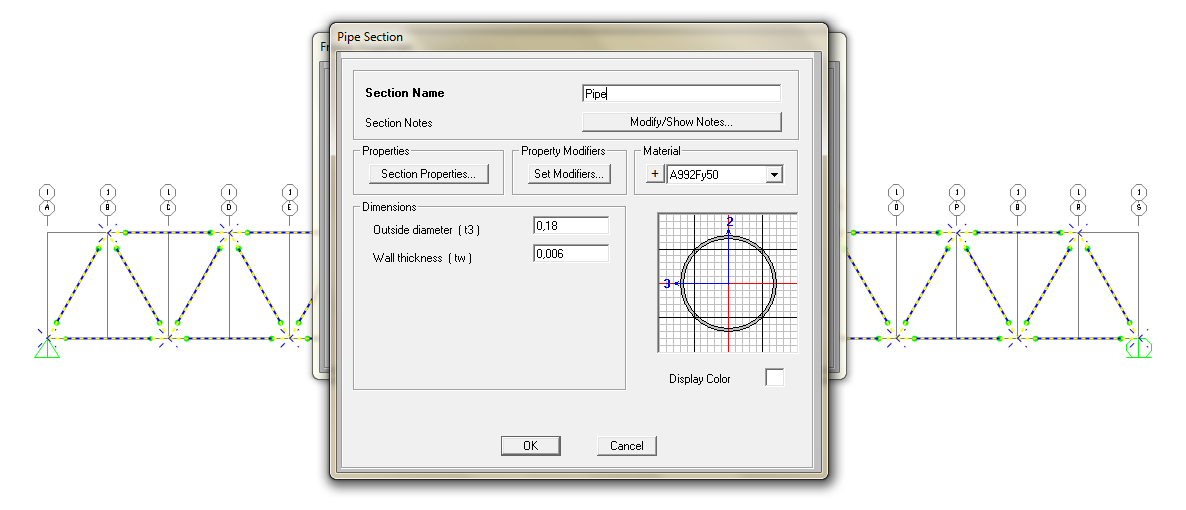
E seleziono il profilato cilindrico in acciaio. Al quale do parametri diametro 18 cm e spessore 6 mm.
E' ora di imporre le forze che esercitano sulla struttura. Essendo una reticolare le forze insistono sui nodi, ecco perché devo stare attento a selezionare solo quelli che mi interessano.

[Assign]>[Joint Loads]>[Forces]
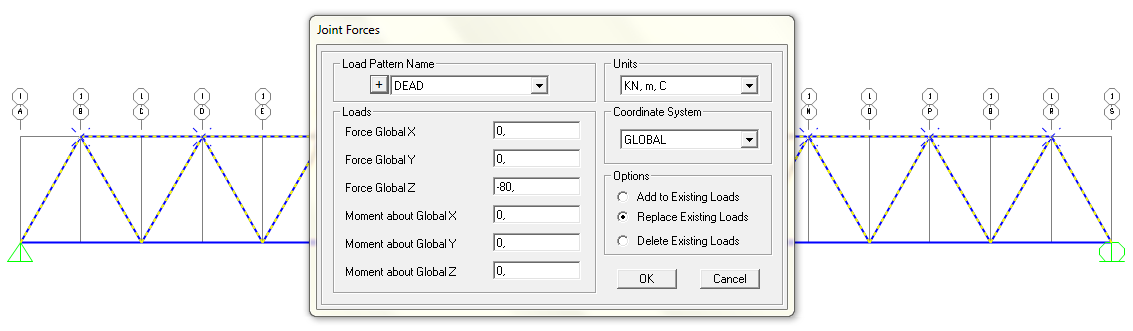
Clicco su + per aggiungere una nuova entità di carico. Scrivo il nome Carico e clicco Add New Load Pattern
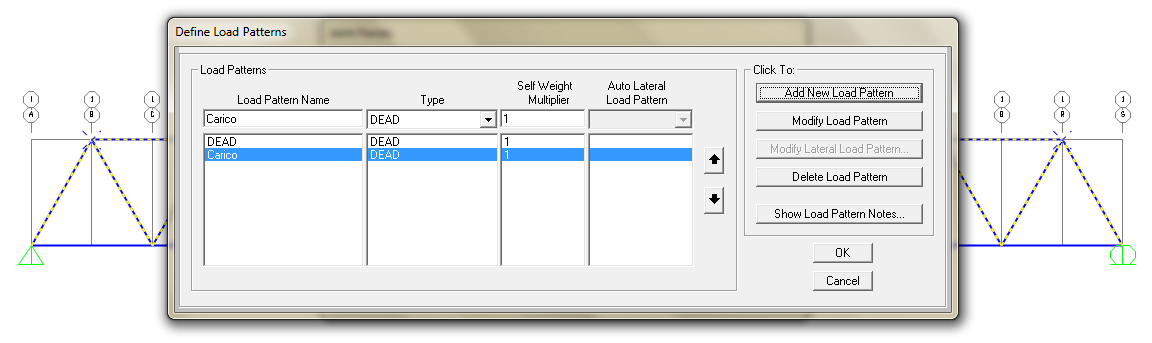
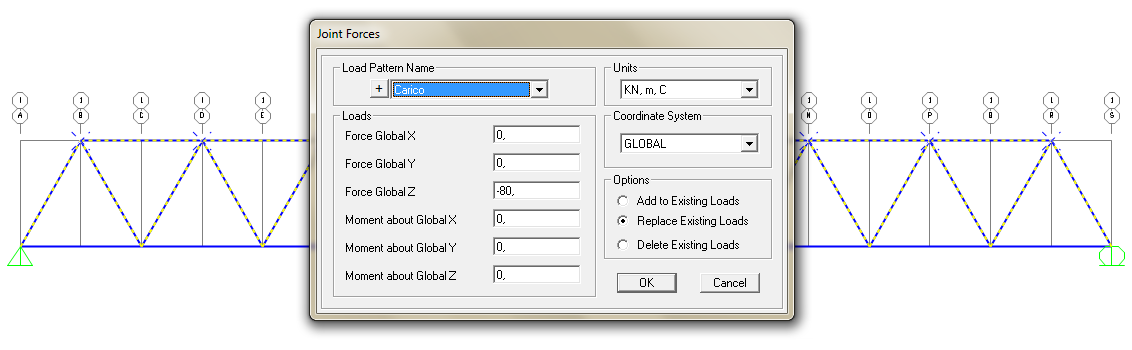
Stando attento a selezionare Carico dal menù a tendina impongo una forza dall'alto che insista sulla struttura. Quindi su Globale Z inserisco il valore -80KN. (Negativo perché verso il basso)
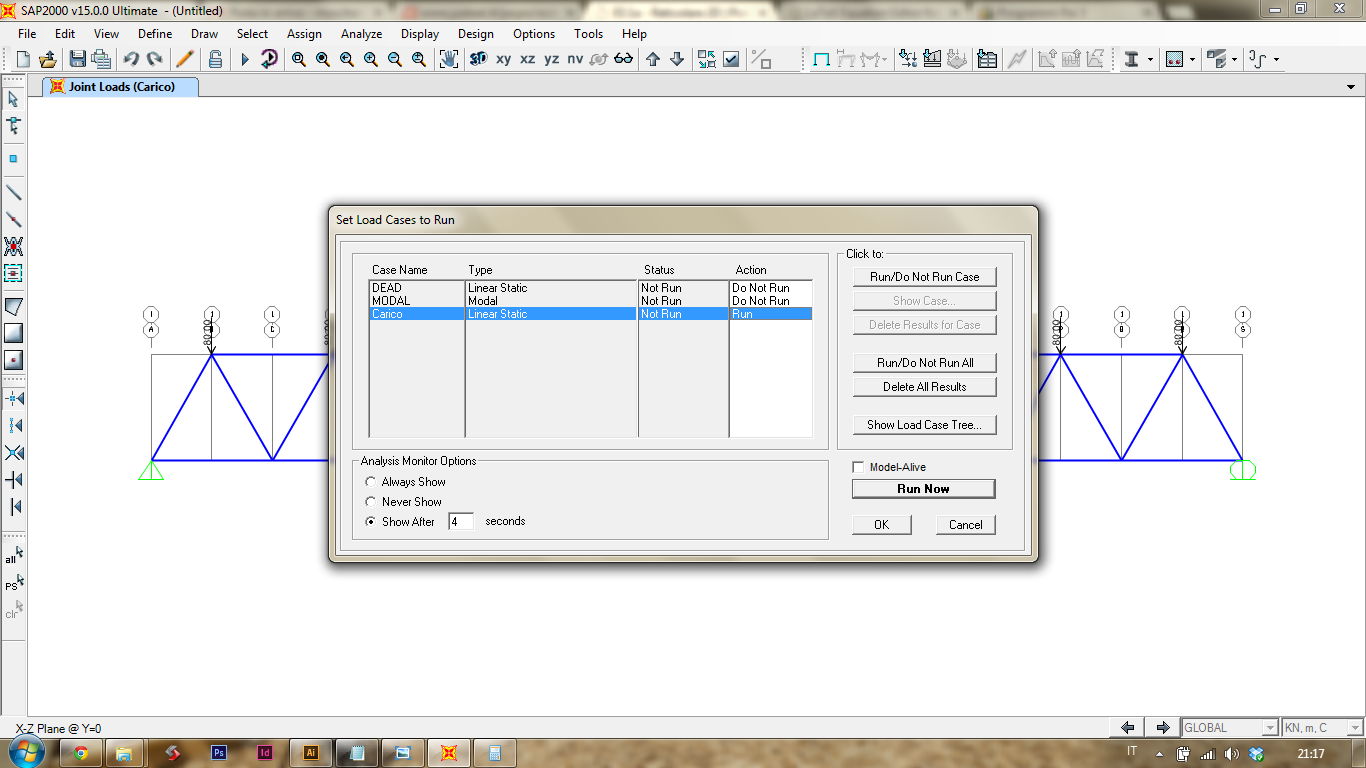
Sono pronto per l'analisi. [Analyze]>[Run Analysis]. Devo solo avere l'accortezza di inserire in analisi solo l'azione delle forze che ho imposto. Quindi dando Run/Do not Run Case in modo che resti selezionato solo Carico.
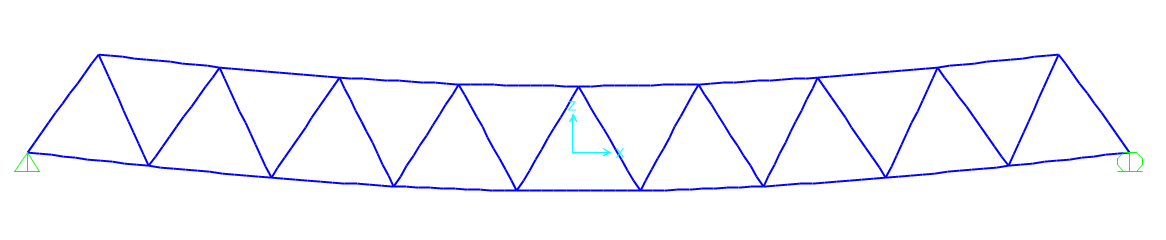
SAP2000 mostra subito la deformata, poco rassicurante, della struttura.
Adesso posso andare a vedere il diagramma dello sforzo normale. Ma prima voglio vedere il numero delle aste in modo da poter confrontare i risultati.
[View]>[Set Display Options] e selezionare Labels dalla seconda colonna. In questo modo ogni asta avrà un suo "nome", o meglio un numero.
[Display]>[Show Forces/Stresses]>[Frame/Cables/Tendons] e selezionando Axial Forces posso vedere il diagramma che mi interessa. In basso alla finestra si può Anche selezionare Fill Diagram o Show Values on Diagram, i quali rispettivamente mostrano un semplice diagramma colorato oppure permette di vedere i valori direttamente sul diagramma.
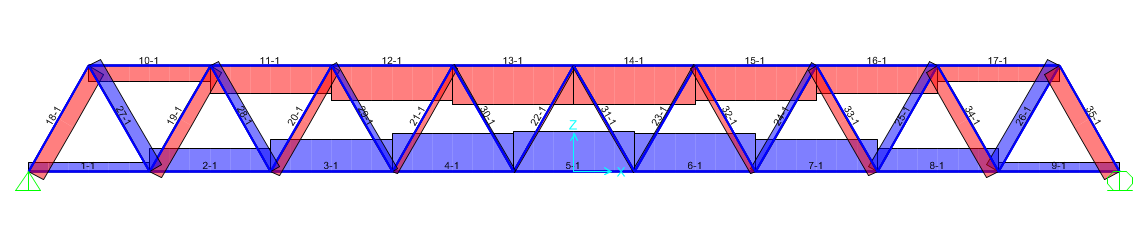
Beh sembra proprio che c'abbia preso.
Ora posso visualizzare anche le tabelle con tutti i valori. [Display]>[Show Table]. Selezionando dal sottomenù di Analysis Results > Element Output. La tabella che mi interessa è Element Forces - Frames.
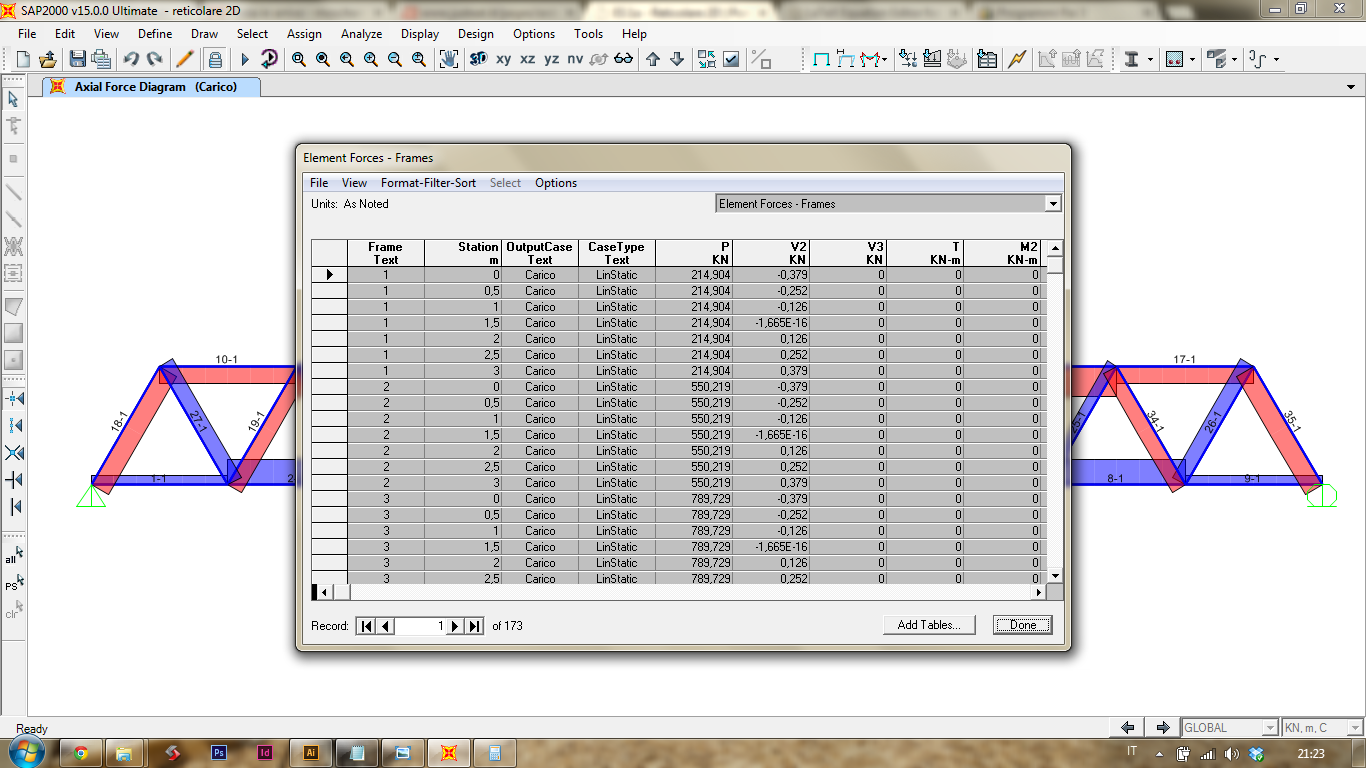
La tabella che mi si presenta ha molti valori. Per ogni asta vengono mostrate molte sezioni, essendo però lo sforzo normale costante posso selezionare solo una delle sezioni per ogni asta. Questo e molto altro per "pulire" la tabella ancor prima di esportarla si può fare dal menù [Format-Filter Sort] > [Filter Table]. Il valore che ci interessa dello sforzo normale è nella colonna P
[File] > [Export Current Table] > [To Excel]
I valori delle aste più sollecitate sono:
ASTA 5 = 981,338 KN tirante ASTA 13 = ASTA 14 = -957,824 KN puntone
E' anche interessante valutare la tensione esercitata sulle aste. Per questo una volta calcolata l'area della sezione (6669mm2) ho anche valutato σ=N/A.
ASTA 5 = 147,14 N/mm2 ASTA 13 = ASTA 14 = -143,6 N/mm2
Questi valori ci permettono di controllare se questa struttura può reggere il carico senza superare il limite di snervamento (quello cioè di una tensione ammissibile). Secondo normativa gli acciaio partono da un valore di Tensione di snervamento caratteristica pari a 235 MPa, direi che ci siamo.
Per tutti gli altri valori, allego la tabella excel.
