ES 6 - Gli archi

In quest'ultima esercitazione farò un veloce studio del comportamento degli archi.

Arco a tutto sesto - F (freccia dell'arco) = L (distanza dall'imposta dell'arco alla proiezione a terra della chiave)

Arco a sesto acuto - F > L

Arco a sesto ribassato - F < L

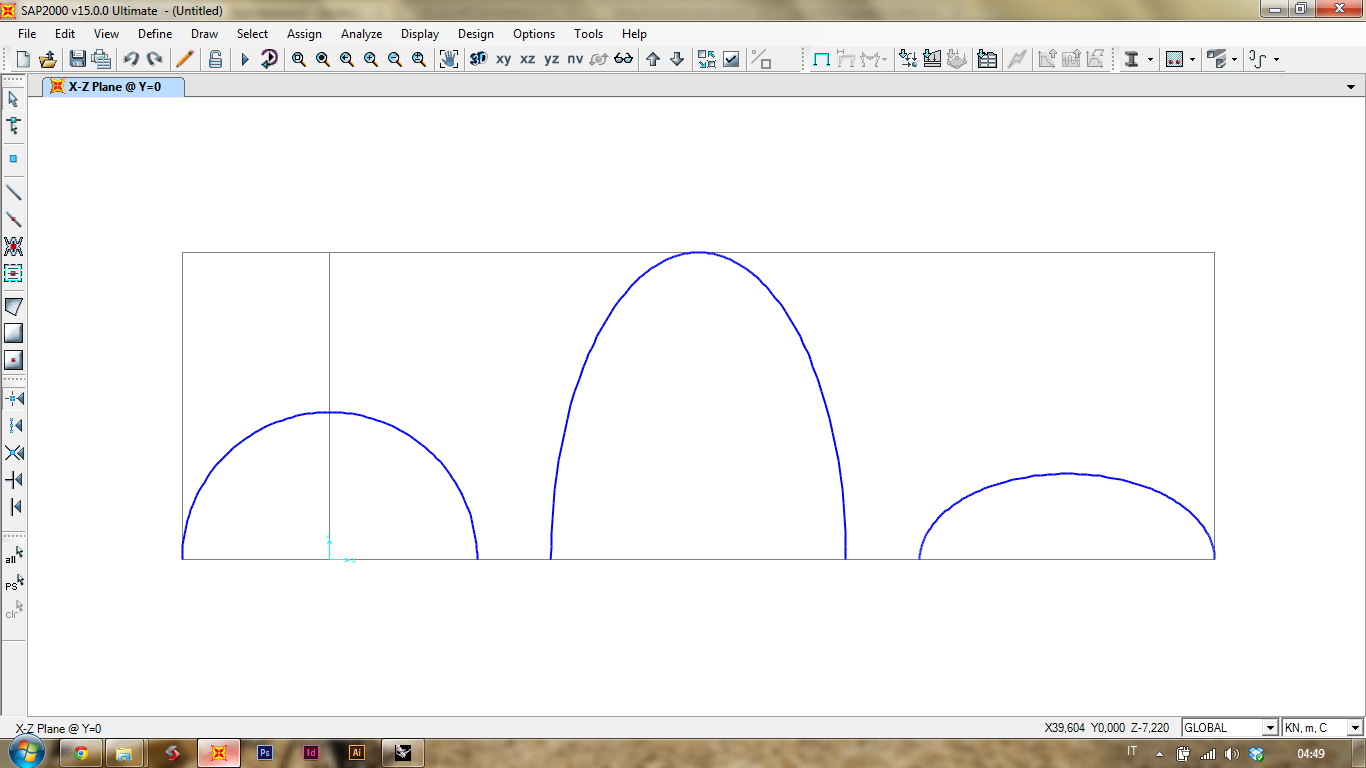
Ho disegnato i tre archi in Rhino per poi importarli in Sap. Ho sistemato il modello per evitarne "errori":

- ho usato il comando Merge Joints perché le curve importate erano in verità segmenti accostati. Questo comando mi permette di garantire una curva continua

- alla chiave di ogni arco ho annullato il trasporto del momento usando il comando Release/Partial Fixity. (come se ci fosse una cerniera)

Ad ogni imposta dell'arco ho assegnato un vincolo cerniera. Infine imposto anche la sezione della trave.

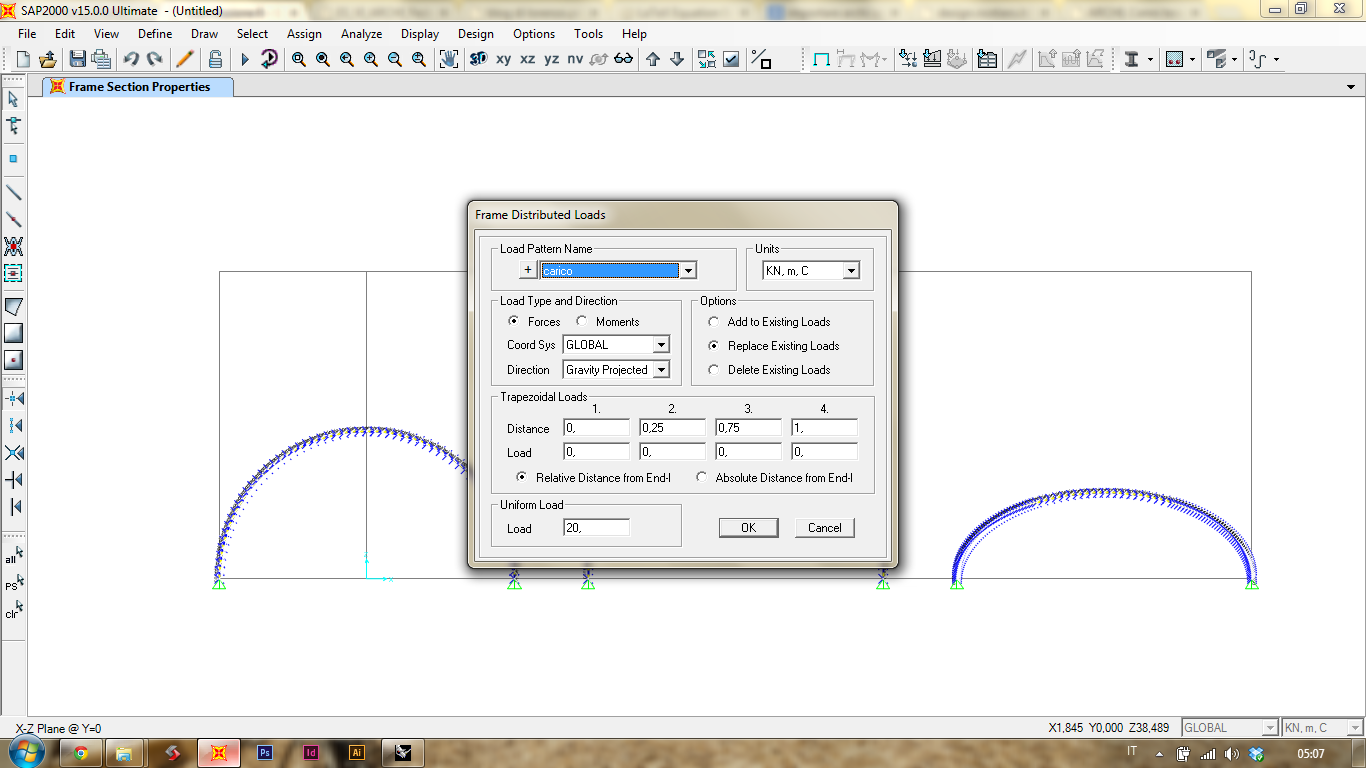
Impongo un carico uniformemente distribuito (20KN)che agisca su una luce pari a quella degli archi (Gravity Projected)

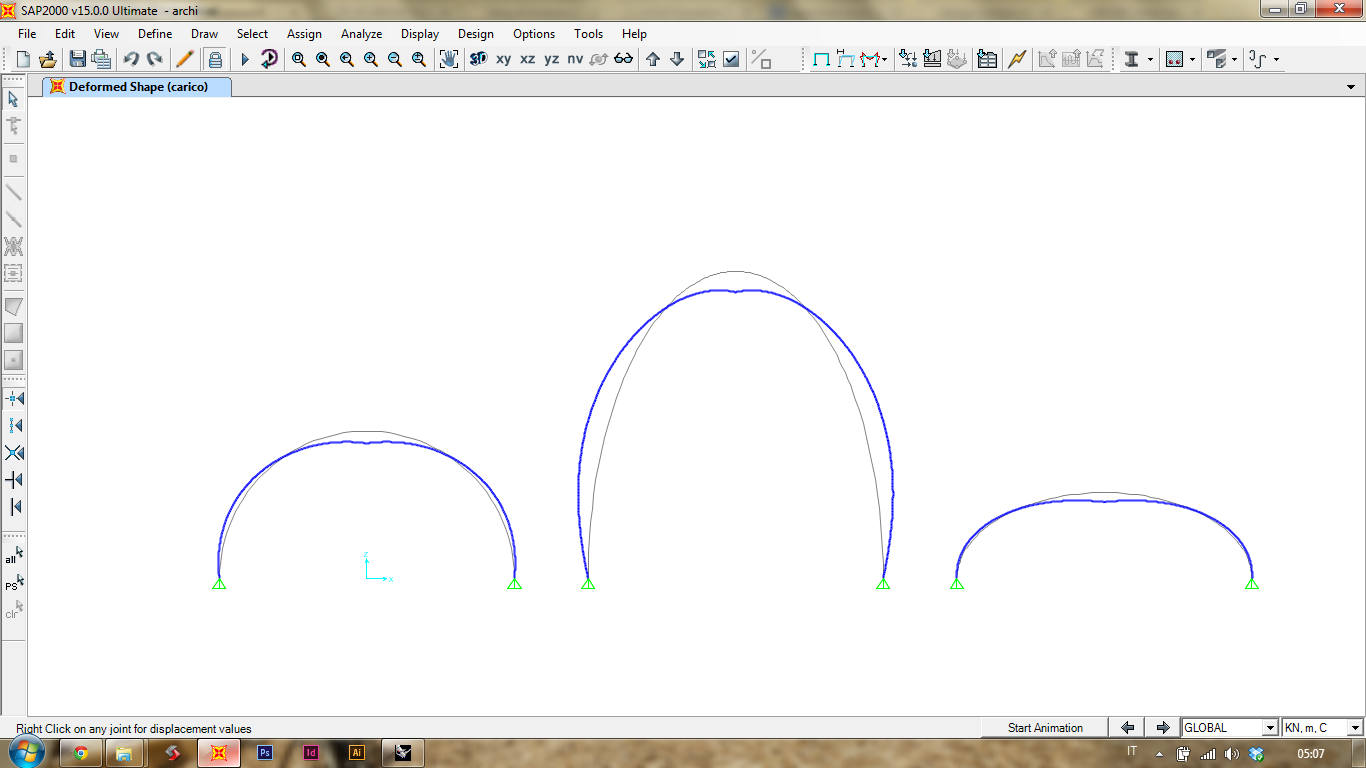
Ora posso far partire l'analisi. Ecco la deformata.

Posso anche vedere i diagrammi di Sforzo Normale, Taglio e Momento.

N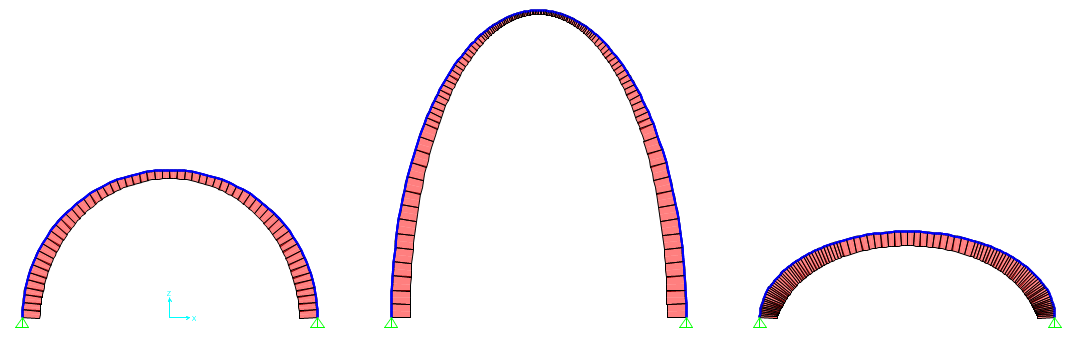   

T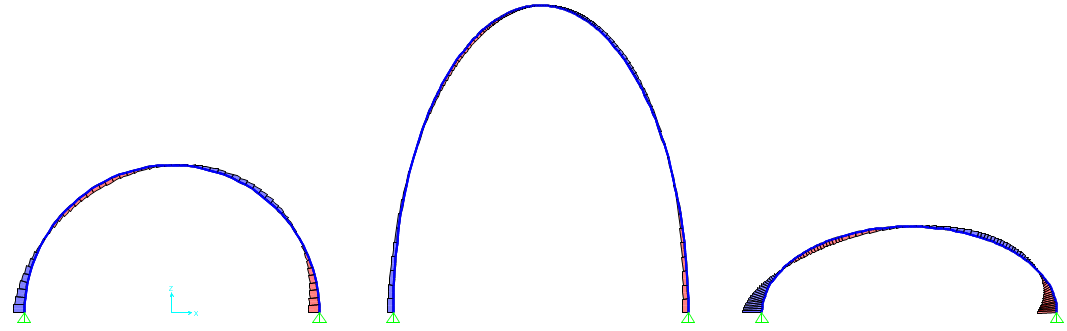    

M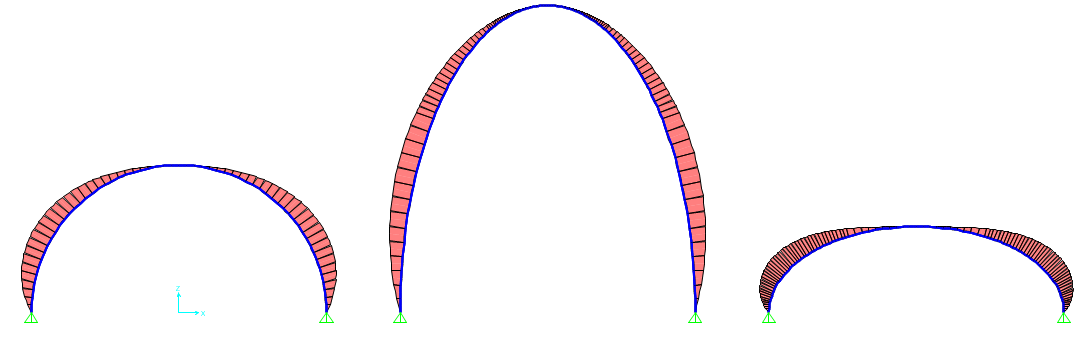   

Soprattutto Sforzo Normale e Taglio sono interessanti da analizzare in quanto essi sono strettamente legati alle reazioni vincolari delle cerniere all'imposta. Si può notare infatti che più ci si sposta verso l'imposta dell'arco e più la spinta dell'arco aumenta. Essa è infatti l'opposto delle reazioni vincolari.

In particolare questa, dipende dalla freccia dell'arco che più è bassa e più è alta la spinta. Se andiamo a vedere nelle tabelle SAP le reazioni vincolari delle cerniere possiamo notare che l'arco a tutto sesto ha una spinta quasi due volte superiore a quella dell'arco acuto ma molto inferiore rispetto a quella dell'arco ribassato.