I ESERCITAZIONE_ Dimensionamento trave in cls, in acciaio e in legno

La struttura è definibile come l’insieme di tutti quegli elementi la cui funzione principale consiste nel resistere alle azioni che l’ambiente esterno esercita sulla struttura stessa.

La natura di queste azioni è varia può dipendere da agenti esterni o dal peso stesso della struttura. Il peso e le altre azioni devono essere trasmesse al terreno, in modo tale che le reazioni vincolari, annullando le azioni, possano garantire l’equilibrio della costruzione.

Le azioni si classificano secondo la loro durata e possono essere permanenti o variabili, quelle permanenti sono le azioni che permangono per tutta la vita utile della struttura, quelle variabili tengono conto delle condizioni ambientali e della destinazione d’uso dell’edificio (carichi di esercizio), delle condizioni eccezionali (incendi, esplosioni ecc.) e delle condizioni sismiche.

Le azioni permanenti a loro volta si suddividono in strutturali e non strutturali, le prime sono legate al peso proprio del materiale le seconde individuano opere non strutturali ma comunque fisse (es. pavimento, impermeabilizzazione ecc.).

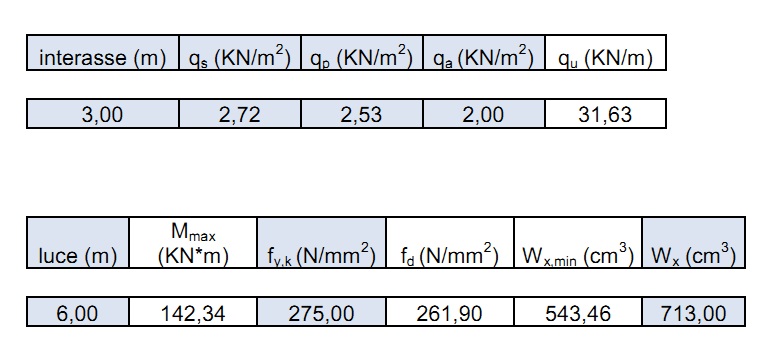
Per poter dimensionare la trave più sollecitata del solaio rappresentato in fig.1 è necessario individuare le azioni permanenti strutturali q_S, non strutturali q_p e le azioni variabili q_a (espresse in KN/m² ) in modo da inserirle nell’equazione di combinazione dei carichi ( in questo caso sarà la combinazione dei carichi allo SLU).

γ_{G1 =  coefficiente di combinazione dei carichi permanenti strutturali pari a 1,3}

γ_{G2 = coefficiente di combinazione dei carichi permanenti non strutturali pari a 1,5}

γ_{q = coefficiente di combinazione del carico variabile principale pari a 1,5}

 

Attraverso l’equazione di combinazione dei carichi sarà possibile ottenere un carico totale q_t, ovvero il carico agente su un metro quadrato di solaio.

A questo punto è necessario ricavare il carico agente sulla trave più sollecitata evidenziata in fig.1, in KN/m, quindi si trova l’area d’influenza della trave

A = interasse x luce

Carico area influenza trave (q_{area inf. trave} )= q_t x A    =    (q_{area inf. trave} )= q_t x i x l

Trovato il carico agente sulla fascia di influenza è possibile, dividendo per l, ottenere il carico lineare incidente sulla trave (q _lineare), passando quindi da un modello tridimensionale di trave a fibre ( trave di Galileo) al modello di trave di Bernoulli bidimensionale, in cui la trave è ridotta a un asse baricentrico.

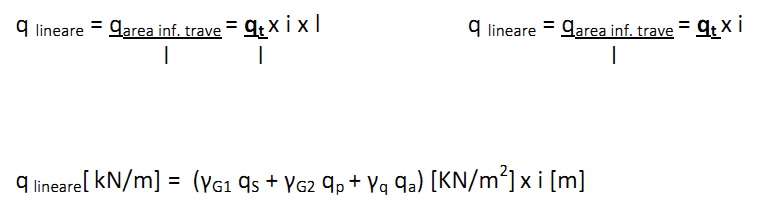
Procediamo quindi con l’individuazione dei carichi per quel che riguarda un solaio in cls con luce di 6 m e interasse di 3 m.

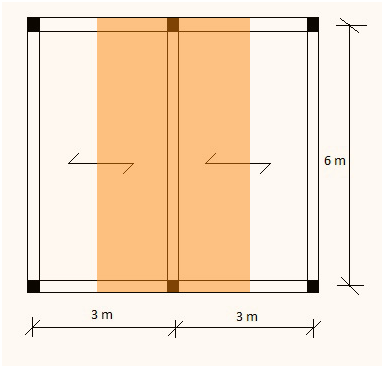Fig.1

SOLAIO IN CLS

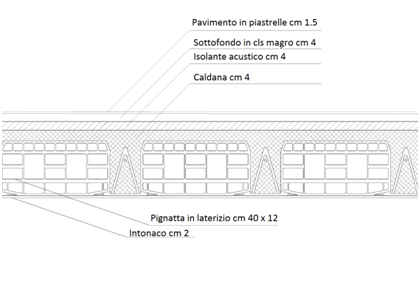
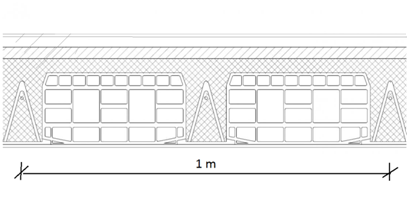Fig. 2

 

q _{a  TOTALE}   2 KN/m²  edifici residenziali

( in questo caso consideriamo tra tutti i carichi variabili solo il carico di esercizio per edifici residenziali)

 

q_{t =} γ_G1 q_S + γ_G2 q_p + γ_q q_a + Ʃ γ_q Ψ q_a

q_t = ( 1.3 x 2.12) + ( 1.5 x 3) + ( 1.5 x 2 ) = 10.25  KN/ m²    (carico su un metro quadro di solaio)

q _lineare[ kN/m] =  (γ_G1 q_S + γ_G2 q_p + γ_q q_a) [KN/m²] x i [m]

q_u = 10.25 [KN/m²] x 3 [m] = 30.77  kN/m   (carico lineare incidente sulla trave)

Queste operazioni vengono svolte direttamente nella tabella Excel  immettendo i carichi.

In questo caso si sta studiando una trave appoggiata appoggiata con carico uniformemente distribuito il cui momento è ql²/8

Quindi sostituendo il carico q_u a q  e la luce si otterrà:

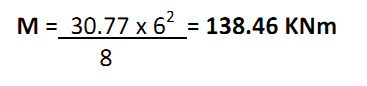
Per le armature si sceglie una resistenza caratteristica fyk=450 MPa (la tensione caratteristica di snervamento) da questa si ricava fyd, poiché:

fyd= fyk/γ_s,

dove γ_s è il coeff. di sicurezza dell’acciaio da cemento armato pari a 1.15.     

 

Per il cls si sceglie C 40/50 ( il primo valore si riferisce alla resistenza caratteristica cilindrica fck in compressione e il secondo alla resistenza caratteristica cubica Rck in compressione ).

Dalla fck è possibile ricavare la fcd, poiché:

fcd= α fck/γ_s ,

dove α è il coeff. Che tiene conto delle deformazioni lente

γ_c è il coeff. di sicurezza relativo al calcestruzzo pari a 1.5.     

Quindi è possibile scegliere la base b=30cm e ottenere l’altezza minima della sezione della trave maggiormente sollecitata pari a 37.20 cm,  ingegnerizzando si porta l’altezza a 40 cm.

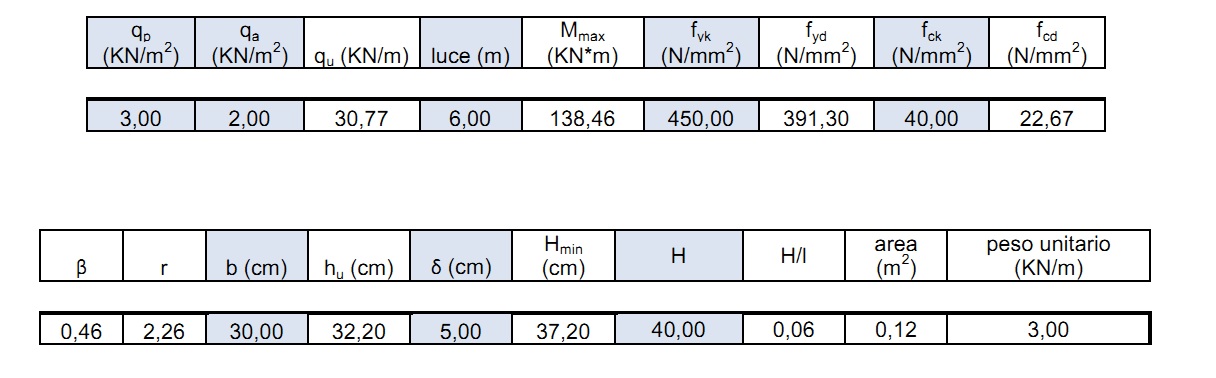
Si ottiene il peso unitario della trave ingegnerizzata, utile per la verificare se l’altezza scelta e quindi la sezione è in grado di supportare i carichi calcolati.

Verifica

 

SOLAIO IN ACCIAIO

 

                      

q _{a  TOTALE}   2 KN/m²  edifici residenziali

( in questo caso consideriamo tra tutti i carichi variabili solo il carico di esercizio per edifici residenziali)

q_{t =} γ_G1 q_S + γ_G2 q_p + γ_q q_a + Ʃ γ_q Ψ q_a

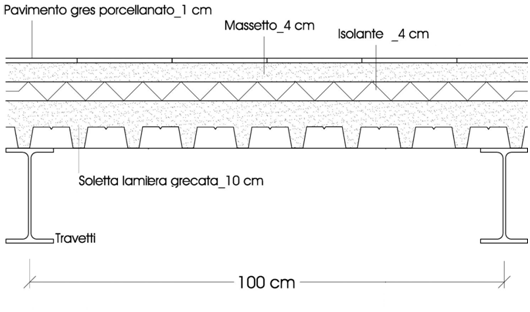
q_t = ( 1.3 x 2.72) + ( 1.5 x 2.53) + ( 1.5 x 2 ) = 10.32  KN/ m²    (carico su un metro quadro di solaio)

q _lineare[ kN/m] =  (γ_G1 q_S + γ_G2 q_p + γ_q q_a) [KN/m²] x i [m]

q_u = 10.32  [KN/m²] x 3 [m] =  31.63  kN/m   (carico lineare incidente sulla trave)

Queste operazioni vengono svolte direttamente nella tabella Excel  immettendo i carichi .

In questo caso si sta studiando una trave appoggiata appoggiata con carico uniformemente distribuito il cui momento è ql²/8

Quindi sostituendo il carico q_u a q  e la luce si otterrà:

Si sceglie una S275 con f yk = 275 Mpa (tensione caratt. di snervamento)

Dalla fyk è possibile ricavare la fyd, poiché:

f yd=  fyk/γ_s         

In fine si ottiene  W x,min dalla formula sottostante potendo così scegliere l’IPE.

W x,min = Mmax / f yd     

                  

 Si sceglie IPE 360 con W_x = 903 cm³

Per verificare è possibile aggiungere il peso della trave ai carichi q_u, il peso della trave IPE 360 è pari a 57.9 Kg/m.

Come si può notare nel caso dell’acciaio il peso stesso della trave è poco influente infatti q_u varia di poco e dunque la sezione è verificata.

SOLAIO IN LEGNO

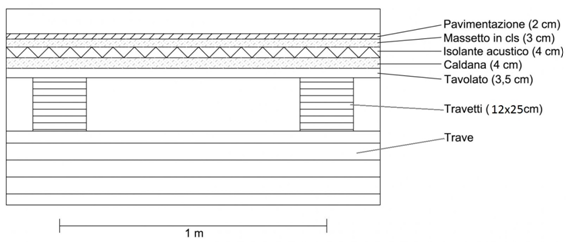
q _{a  TOTALE}   2 KN/m²  edifici residenziali

( in questo caso consideriamo tra tutti i carichi variabili solo il carico di esercizio per edifici residenziali)

 

q_{t =} γ_G1 q_S + γ_G2 q_p + γ_q q_a + Ʃ γ_q Ψ q_a

q_t = ( 1.3 x 0.39) + ( 1.5 x 3.07) + ( 1.5 x 2 ) =  8  KN/ m²    (carico su un metro quadro di solaio)

q _lineare[ kN/m] =  (γ_G1 q_S + γ_G2 q_p + γ_q q_a) [KN/m²] x i [m]

q_u = 8 [KN/m²] x 3 [m] =24.34  kN/m   (carico lineare incidente sulla trave)

Queste operazioni vengono svolte direttamente nella tabella Excel  immettendo i carichi .

In questo caso si sta studiando una trave appoggiata appoggiata con carico uniformemente distribuito il cui momento è ql²/8

Quindi sostituendo il carico q_u a q  e la luce si otterrà:

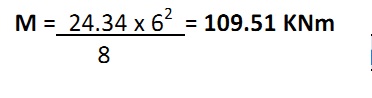
Si sceglie un legno lamellare GL 24h che ha una resistenza a flessione  f mk = 24 Mpa  e grazie alla quale sarà possibile calcolare la tensione di progetto.

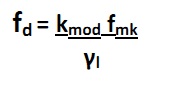
dove:

k_mod  è un coefficiente diminutivo dei valori di resistenza del materiale

f_mk   è la resistenza caratteristica del legno

γ_l   coeff. parziale di sicurezza nel caso del legno lamellare è pari a 1.45

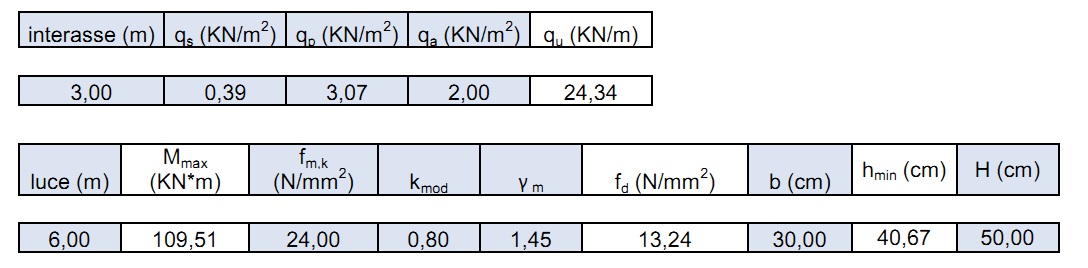
h_min= 40.67 ingegnerizzando l’altezza si porta a 50 cm.

Ora è possibile verificare la sezione inserendo nel calcolo del q_u  anche il peso della trave.

Peso unitario legno 6 KN/m³            

(0.30 x 0.50 x 1 ) mc x 6 KN/m³  = 0.9 KN/m

 

Come si può notare nel caso del legno il peso stesso della trave è poco influente infatti q_u varia di poco e dunque la sezione è verificata.