Esercitazione3_Dimensionamento e verifica deformabilità mensola

La terza esercitazione prevede il dimensionamento e la verifica di deformabilità della mensola più sollecitata del solaio di carpenteria in tre diverse tecnologie: legno, acciaio e cemento armato.

Utilizzeremo un foglio di calcolo Excel, molto simile a quello della prima esercitazione, ma in questo caso diviso in due parti diverse.
Una prima parte, in cui ragioniamo in termini di SLU, uguale al foglio utilizzato nella prima esercitazione.
Una seconda parte, in cui invece ragioniamo in termini di SLE, in cui otteniamo i valori relativi allo spostamento e la deformabilità della mensola.
Questi due tipi di analisi diversi presuppongono inoltre coefficienti di sicurezza diversi.

Legno

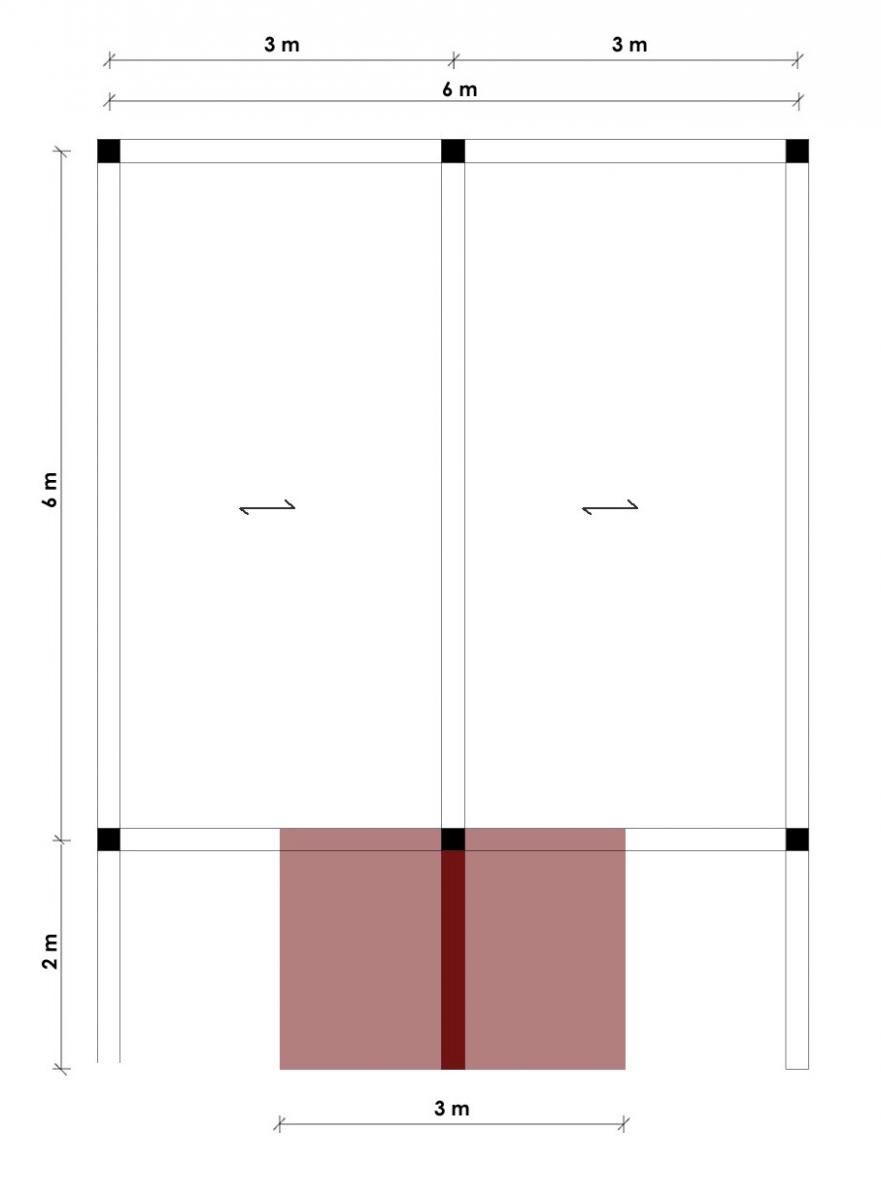
Per questo solaio  la mensola maggiormente sollecitata è quella centrale, che presenta una luce di 2m e un interasse di 3m.
Poiché il solaio preso in considerazione è lo stesso della prima esercitazione, i valori dei diversi carichi presenti (strutturale, permanente e accidentale) sono gli stessi.

Inserendo i valori ottenuti nel foglio di calcolo excel, otteniamo il valore del carico ultimo, ottenuto moltiplicando i diversi carichi agenti per i rispettivi coefficienti di sicurezza.

Ottenuto il valore del carico ultimo possiamo inoltre trovare il valore del momento massimo, che per una mensola, di lunghezza l e sottoposta a carica q, equivale a  ql²/2.

Per il progetto scegliamo un legno lamellare GL24H, con resistenza a flessione caratteristica
fm,k = 24 MPa, e scegliamo come coefficiente di durata del carico kmod = 0,8 e come coefficiente parziale di sicurezza del materiale γ m = 1,45.
Con l’utilizzo di questi dati è possibile calcolare la tensione ammissibile di progetto fd.

Impostando in seguito la base della trave da calcolare, ci viene fornita l’altezza minima della stessa.

Scegliendo quindi una base di 25 cm otteniamo un’altezza minima di circa 31 cm.
Essendo questo valore il valore minimo dell’altezza della trave, scegliamo un’altezza di 40 cm, ottenendo una trave di sezione 25cm x 40 cm.

Dopo aver dimensionato la trave inizia la parte relativa allo SLE, inserendo il valore del modulo elastico del legno, E = 8000 MPa, ottengo i valori del carico allo SLE, qe, che non tiene in considerazione il peso proprio della trave, essendo il legno un materiale leggero, del momento di inerzia, I_x, e dello spostamento massimo, v_max = 0,26 cm.
Questo dato mi conferma il progetto, in quanto il rapporto tra il momento di inerzia e quello dello spostamento è maggiore di 250 ( I_x/ v_max >250).

Acciaio

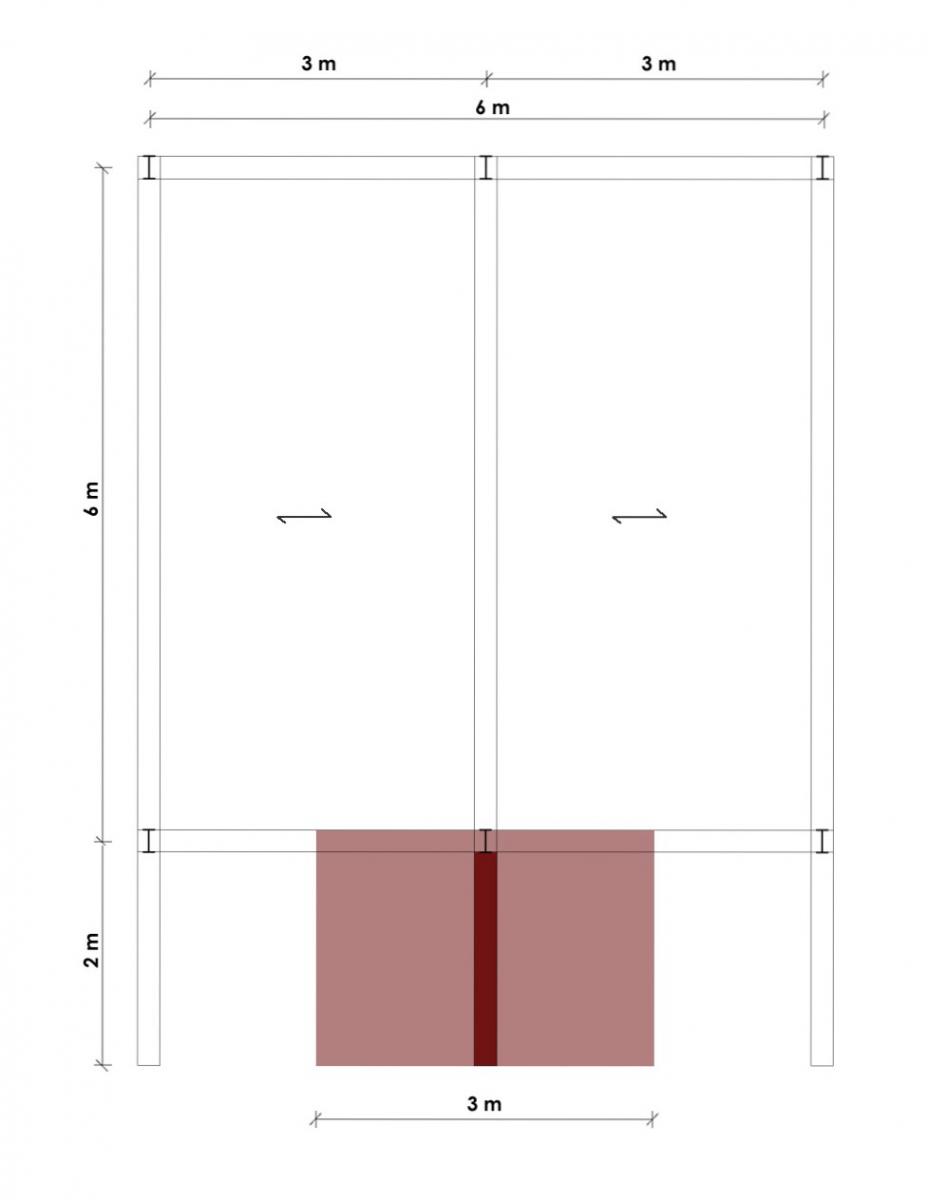
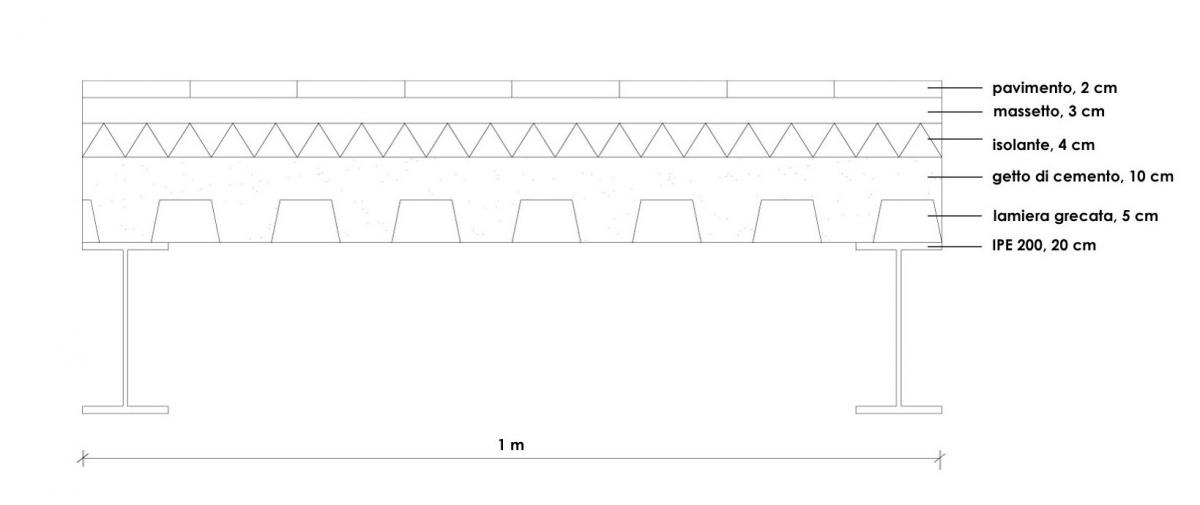
Per questo solaio  la mensola maggiormente sollecitata è quella centrale, che presenta una luce di 2m e un interasse di 3m.
Poiché il solaio preso in considerazione è lo stesso della prima esercitazione, i valori dei diversi carichi presenti (strutturale, permanente e accidentale) sono gli stessi.

Inserendo i valori ottenuti nel foglio di calcolo excel, otteniamo il valore del carico ultimo, ottenuto moltiplicando i diversi carichi agenti per i rispettivi coefficienti di sicurezza.

Ottenuto il valore del carico ultimo possiamo inoltre trovare il valore del momento massimo, che per una mensola, di lunghezza l e sottoposta a carica q, equivale a  ql²/2.

Per il progetto di questa trave scegliamo un acciaio S235 con resistenza a flessione caratteristica
fy,k = 235 MPa.

Con l’utilizzo di questi dati è possibile calcolare la tensione ammissibile di progetto fd, e il modulo di resistenza Wx minimo, di circa 260 cm3.

Scegliamo quindi una trave IPE 240, con modulo di resistenza Wx pari a 324,3 cm3, momento di inerzia Ix pari a 3892 cm4, e peso di 0,307 kN/m.

Anche in questo caso, inserendo questi dati, e il modulo elastico dell’acciaio E = 210000 MPa, otteniamo i valori del carico allo SLE, qe, che in questo caso tiene in considerazione anche il peso proprio della trave, e dello spostamento massimo, v_max = 0,438 cm.
Questo dato mi conferma il progetto, in quanto il rapporto tra il momento di inerzia e quello dello spostamento è maggiore di 250 ( I_x/ v_max >250).

Cemento armato

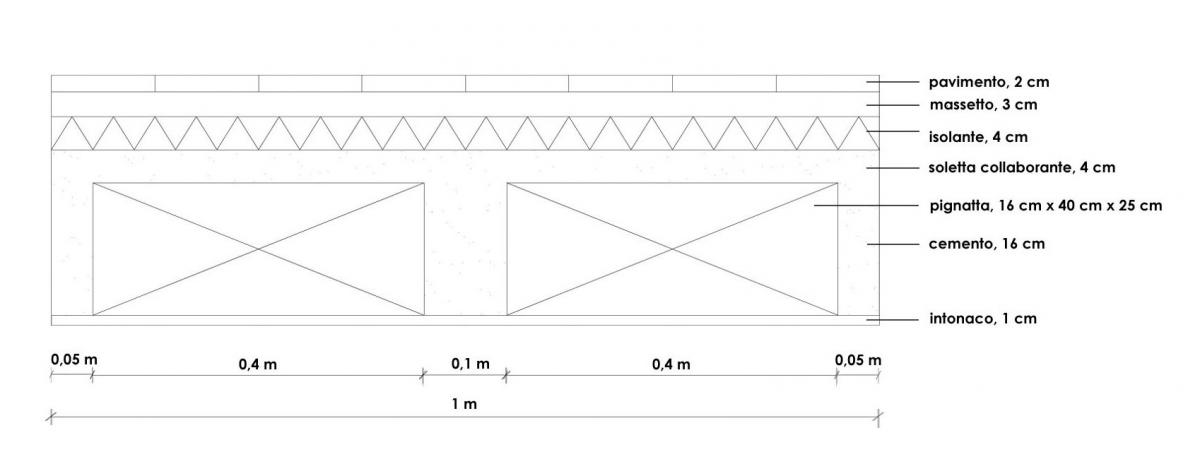
Per questo solaio  la mensola maggiormente sollecitata è quella centrale, che presenta una luce di 2m e un interasse di 3m.
Poiché il solaio preso in considerazione è lo stesso della prima esercitazione, i valori dei diversi carichi presenti (strutturale, permanente e accidentale) sono gli stessi.

Inserendo i valori ottenuti nel foglio di calcolo excel, otteniamo il valore del carico ultimo, ottenuto moltiplicando i diversi carichi agenti per i rispettivi coefficienti di sicurezza.

Ottenuto il valore del carico ultimo possiamo inoltre trovare il valore del momento massimo, che per una mensola, di lunghezza l e sottoposta a carica q, equivale a  ql²/2.

Per il progetto di questa trave scegliamo per l’armatura un acciaio con resistenza a flessione caratteristica fy,k = 450 MPa, e un calcestruzzo con resistenza fc,k = 60 MPa.

Con l’utilizzo di questi dati è possibile calcolare le tensioni di progetto fyd e fcd, rispettivamente dell'acciaio e del cemento.
Impostando in seguito la base della trave da calcolare e la dimensione del copriferro, ci viene fornita l’altezza utile e l’altezza minima della stessa.

Scegliendo quindi una base di 20 cm e un copriferro di 5 cm, otteniamo un’altezza utile di circa 20 cm, e quindi una altezza minima di circa 25 cm.
Essendo questo valore il valore minimo dell’altezza della trave, scegliamo un’altezza di 30 cm, ottenendo una trave di sezione 20 cm x 30 cm.

Con l’utilizzo di questi dati è possibile calcolare l’area e il peso della trave, che viene tenuto in considerazione nel calcolo del carico allo SLE, in quanto il cemento armato non ha un peso trascurabile.

Anche in questo caso, inserendo questi dati, e il modulo elastico E, otteniamo i valori del carico allo SLE, qe, del momento di inerzia, I_x, e dello spostamento massimo, v_max = 0,42 cm.
Questo dato mi conferma il progetto, in quanto il rapporto tra il momento di inerzia e quello dello spostamento è maggiore di 250 ( I_x/ v_max >250).