blog di Marta Faienza

La quinta esercitazione consiste nel calcolare la ripartizione di una forza orizzontale, come il sisma o il vento, sui diversi telai che compongono una struttura, attraverso il metodo delle rigidezze. 

Prendiamo in considerazione un generico edificio, il cui piano tipo è costituito da telai shear-type, un particolare tipo di telaio in c.a. che, oltre a trasmettere i carichi verticali a terra, è capace di svolgere il ruolo di controvento.

Step 1: calcolo delle rigidezze traslanti dei controventi dell'edificio

In pianta possiamo rappresentare i controventi come molle, ovvero vincoli cedevoli elastici, che esercitano una forza reattiva, ma subiscono comunque una deformazione.

Nella prima parte del foglio Excel ricaviamo la rigidezza traslante di ogni telaio, inserendo i dati relativi ai pilastri che compongono i telai stessi. Essendo i pilastri di sezione rettangolare, in particolare 30x50 cm avranno momenti di inerzia diversi in base al loro orientamento. I due valori ottenuti sono 112500,00 cm⁴ e 312500,00 cm⁴.

Step 2

Nello step 2 del foglio Excel sono riportate le rigidezze di ogni telaio, e la loro distanza relativa dall’origine.

Step 3 : calcolo del centro di massa

Nello step 3 del foglio Excel possiamo calcolare il centro di massa dell’impalcato in considerazione.
Per questo suddividiamo l’impalcato in due figure geometriche semplici, due rettangoli rispettivamente di area, A₁ e A₂. Infatti dati l’area e il baricentro di ognuno dei due rettangoli possiamo ricavare le coordinate del centro di massa, che risulterà sulla retta congiungente i due diversi centri di massa dei rettangoli.
Le coordinate del centro di massa saranno:

X_g = A₁*X_g1 + +A₂*X_g2 / A_tot  

Y_g = A₁*Y_g1 + A₂*Y_g2 / A_tot

Il centro di massa avrà coordinate G (19,69; 10,03).

Step 4 : calcolo del centro delle rigidezze

Possiamo ora calcolare a questo punto il centro delle rigidezze con il foglio Excel. Le cui coordinate risulteranno:

X_c= K_v1*d_v1 + K_v2*d_v2 + ... + K_vn*d_vn/ K_vtot 

Y_c= K_o1*d_o1 + K_o2*d_o2 + ...... + K_on*d_on/ K_otot 

Il centro delle rigidezze avrà coordinate C (19,34; 8,25).

Il centro di massa e il centro delle rigidezze, non sono molto distanti, ma non coincidendo generano un braccio rispetto alla forza applicata, e di conseguenza un momento.

Infatti la forza sismica F, sia in direzione X che in direzione Y, viene applicata nel centro di massa G, e avendo braccio rispetto al centro delle rigidezze C, genererà una rotazione oltre che una traslazione.

Step 5 : analisi dei carichi sismici

Nello step 5 del foglio Excel possiamo, attraverso l’analisi dei carichi sismici, ricavare la forza complessiva che agisce sul centro di massa. Inserendo infatti i valori di qs, qp e qa trovati nella prima esercitazione, per un solaio in laterocemento, e il coefficiente di contemporaneità ψ = 0,3, dato dalla destinazione d’uso dell’edificio, e il coefficiente di intensità sismica c = 0,10, dato dall’area geografica in cui si trova l’edificio, otteniamo il valore della forza sismica orizzontale (F = 280,14 kN).

La forza sismica F verrà applicata sia in X che in Y.

Step 6,7 : ripartizione forza sismica lungo X e lungo Y

In questi ultimi step la forza sismica viene ripartita sui controventi, e possiamo quantificare la cinematica dell’impalcato: la traslazione orizzonte u, la traslazione verticale v, e la rotazione φ.

u = = F/k_{o_tot} 

v = F/k_{v_tot}

φ = W/kφ 

Possiamo schematizzare gli effetti della forza sismica lungo X:

Possiamo schematizzare gli effetti della forza sismica lungo Y:

La quarta esercitazione prevede il dimensionamento del pilastro più sollecitato, attraverso l’utilizzo di un foglio di calcolo excel,  in tre diverse tecnologie: legno, acciaio e cemento armato.

Legno

Considerato il seguente impalcato il pilastro più sollecitato sarà sicuramente il pilastro centrale al piano terra, in quanto su di esso convoglia il peso dei piani superiori. Il pilastro in questione ha un’area di influenza di lati, 6m e 3m, per un’area di 18 mq.

Il foglio di calcolo excel presenta una prima parte che contiene le informazioni relative alla struttura scelta, e quindi l’area di influenza e il peso delle travi, che ci permettono di calcolare lo sforzo normale agente sul pilastro stesso. Questo infatti sarà sicuramente influenzato dal numero di piani della struttura e dai pesi gravanti su di esso.

Una seconda parte del foglio Excel invece contiene le informazioni relative ai carichi del solaio (strutturale, permanente e accidentale), considerando il solaio della prima esercitazione.
Inoltre vengono richiesti i dati relativi alle caratteristiche del materiale in questione.
Attraverso questi dati è possibile determinare una base e una altezza minima.

In questo caso il pilastro ottenuto ha una sezione di 20x30 cm, la cui area è minore dell’area minima richiesta (600 cm2 < 482,9 cm2).

Acciaio

Cosi come per il legno, il pilastro più sollecitato è il pilastro centrale, evidenziato in rosso. Il pilastro in questione ha un’area di influenza di lati, 6m e 3m, per un’area di 18 mq.

Anche in questo caso la prima parte del foglio Excel richiede i dati relativi alla struttura, per calcolare lo sforzo normale agente sul pilastro.

Nella seconda parte possiamo inserire i dati relativi alle caratteristiche del materiale scelto, che ci forniscono una area minima, e un momento di inerzia minimo. Attraverso questi dati è possibile dimensionare il pilastro con un profilato HEA che rispetti i requisiti minimi.

In questo caso la sezione del pilastro sarà un profilato HEA160.

Cemento

Poiché la struttura presa in considerazione è la stessa scelta per le precedenti tecnologie, il pilastro maggiormente sollecitato sarà sempre il pilastro centrale, con la stessa area di influenza, di 18 mq.

Inserendo i dati relativi alla struttura nel foglio Excel possiamo ottenere il valore dello sforzo normale agente sul pilastro in considerazione.

Inserendo ora invece i dati relativi alle caratteristiche del materiale, otteniamo una base e una altezza minima che ci permettono di dimensionare il pilastro, in modo che questo verifichi le precedenti limitazioni.

In questo caso il pilastro avrà una sezione di 20x40 cm, in quanto è la sezione che verifica i requisiti richiesti. Infatti risulta che  σ_max   <  f_cd  (27,34 Mpa < 34 Mpa).

La terza esercitazione prevede il dimensionamento e la verifica di deformabilità della mensola più sollecitata del solaio di carpenteria in tre diverse tecnologie: legno, acciaio e cemento armato.

Utilizzeremo un foglio di calcolo Excel, molto simile a quello della prima esercitazione, ma in questo caso diviso in due parti diverse.
Una prima parte, in cui ragioniamo in termini di SLU, uguale al foglio utilizzato nella prima esercitazione.
Una seconda parte, in cui invece ragioniamo in termini di SLE, in cui otteniamo i valori relativi allo spostamento e la deformabilità della mensola.
Questi due tipi di analisi diversi presuppongono inoltre coefficienti di sicurezza diversi.

Legno

Per questo solaio  la mensola maggiormente sollecitata è quella centrale, che presenta una luce di 2m e un interasse di 3m.
Poiché il solaio preso in considerazione è lo stesso della prima esercitazione, i valori dei diversi carichi presenti (strutturale, permanente e accidentale) sono gli stessi.

Inserendo i valori ottenuti nel foglio di calcolo excel, otteniamo il valore del carico ultimo, ottenuto moltiplicando i diversi carichi agenti per i rispettivi coefficienti di sicurezza.

Ottenuto il valore del carico ultimo possiamo inoltre trovare il valore del momento massimo, che per una mensola, di lunghezza l e sottoposta a carica q, equivale a  ql²/2.

Per il progetto scegliamo un legno lamellare GL24H, con resistenza a flessione caratteristica
fm,k = 24 MPa, e scegliamo come coefficiente di durata del carico kmod = 0,8 e come coefficiente parziale di sicurezza del materiale γ m = 1,45.
Con l’utilizzo di questi dati è possibile calcolare la tensione ammissibile di progetto fd.

Impostando in seguito la base della trave da calcolare, ci viene fornita l’altezza minima della stessa.

Scegliendo quindi una base di 25 cm otteniamo un’altezza minima di circa 31 cm.
Essendo questo valore il valore minimo dell’altezza della trave, scegliamo un’altezza di 40 cm, ottenendo una trave di sezione 25cm x 40 cm.

Dopo aver dimensionato la trave inizia la parte relativa allo SLE, inserendo il valore del modulo elastico del legno, E = 8000 MPa, ottengo i valori del carico allo SLE, qe, che non tiene in considerazione il peso proprio della trave, essendo il legno un materiale leggero, del momento di inerzia, I_x, e dello spostamento massimo, v_max = 0,26 cm.
Questo dato mi conferma il progetto, in quanto il rapporto tra il momento di inerzia e quello dello spostamento è maggiore di 250 ( I_x/ v_max >250).

Acciaio

Per questo solaio  la mensola maggiormente sollecitata è quella centrale, che presenta una luce di 2m e un interasse di 3m.
Poiché il solaio preso in considerazione è lo stesso della prima esercitazione, i valori dei diversi carichi presenti (strutturale, permanente e accidentale) sono gli stessi.

Inserendo i valori ottenuti nel foglio di calcolo excel, otteniamo il valore del carico ultimo, ottenuto moltiplicando i diversi carichi agenti per i rispettivi coefficienti di sicurezza.

Ottenuto il valore del carico ultimo possiamo inoltre trovare il valore del momento massimo, che per una mensola, di lunghezza l e sottoposta a carica q, equivale a  ql²/2.

Per il progetto di questa trave scegliamo un acciaio S235 con resistenza a flessione caratteristica
fy,k = 235 MPa.

Con l’utilizzo di questi dati è possibile calcolare la tensione ammissibile di progetto fd, e il modulo di resistenza Wx minimo, di circa 260 cm3.

Scegliamo quindi una trave IPE 240, con modulo di resistenza Wx pari a 324,3 cm3, momento di inerzia Ix pari a 3892 cm4, e peso di 0,307 kN/m.

Anche in questo caso, inserendo questi dati, e il modulo elastico dell’acciaio E = 210000 MPa, otteniamo i valori del carico allo SLE, qe, che in questo caso tiene in considerazione anche il peso proprio della trave, e dello spostamento massimo, v_max = 0,438 cm.
Questo dato mi conferma il progetto, in quanto il rapporto tra il momento di inerzia e quello dello spostamento è maggiore di 250 ( I_x/ v_max >250).

Cemento armato

Per questo solaio  la mensola maggiormente sollecitata è quella centrale, che presenta una luce di 2m e un interasse di 3m.
Poiché il solaio preso in considerazione è lo stesso della prima esercitazione, i valori dei diversi carichi presenti (strutturale, permanente e accidentale) sono gli stessi.

Inserendo i valori ottenuti nel foglio di calcolo excel, otteniamo il valore del carico ultimo, ottenuto moltiplicando i diversi carichi agenti per i rispettivi coefficienti di sicurezza.

Ottenuto il valore del carico ultimo possiamo inoltre trovare il valore del momento massimo, che per una mensola, di lunghezza l e sottoposta a carica q, equivale a  ql²/2.

Per il progetto di questa trave scegliamo per l’armatura un acciaio con resistenza a flessione caratteristica fy,k = 450 MPa, e un calcestruzzo con resistenza fc,k = 60 MPa.

Con l’utilizzo di questi dati è possibile calcolare le tensioni di progetto fyd e fcd, rispettivamente dell'acciaio e del cemento.
Impostando in seguito la base della trave da calcolare e la dimensione del copriferro, ci viene fornita l’altezza utile e l’altezza minima della stessa.

Scegliendo quindi una base di 20 cm e un copriferro di 5 cm, otteniamo un’altezza utile di circa 20 cm, e quindi una altezza minima di circa 25 cm.
Essendo questo valore il valore minimo dell’altezza della trave, scegliamo un’altezza di 30 cm, ottenendo una trave di sezione 20 cm x 30 cm.

Con l’utilizzo di questi dati è possibile calcolare l’area e il peso della trave, che viene tenuto in considerazione nel calcolo del carico allo SLE, in quanto il cemento armato non ha un peso trascurabile.

Anche in questo caso, inserendo questi dati, e il modulo elastico E, otteniamo i valori del carico allo SLE, qe, del momento di inerzia, I_x, e dello spostamento massimo, v_max = 0,42 cm.
Questo dato mi conferma il progetto, in quanto il rapporto tra il momento di inerzia e quello dello spostamento è maggiore di 250 ( I_x/ v_max >250).

La seconda esercitazione prevede l’analisi di una struttura reticolare tridimensionale, attraverso l’utilizzo del software SAP2000.

Il modello realizzato con SAP, ha un modulo di base quadrato, ed è quindi una struttura reticolare formata da diversi cubi reticolari.

Il primo passo è quello di realizzare il modello con SAP, che nel mio caso ha come modulo di base un quadrato, di lato 2m per 2m. La griglia con cui viene realizzato il modello tridimensionale, che è quindi formato da diversi cubi, varia in modo diverso su x,y e z.
Attribuendo i diversi valori, x=3, y=4 e z=2, ottengo un modello formato da sei cubi di lato 2m, e  con diagonali di 2,83 m.

In seguito, dopo aver verificato che nella struttura non ci siano duplicati delle stesse aste, assegniamo la cerniera come vincolo ai quattro appoggi angolari.
Inoltre svincoliamo i nodi al momento in tutte le direzioni, in quanto la struttura reticolare lavora a solo sforzo normale, di trazione o compressione.

Un ulteriore passo è quello di definire un materiale, in questo caso un tubolare in acciaio, e assegnare ai nodi superiori una forza, in questo caso F pari a 150 kN.

A questo punto è possibile far partire l’analisi lineare statica, che ha come oggetto l’azione della forza F, da noi impostata.

Posso adesso vedere la struttura deformata e i diagrammi delle sollecitazioni, a cui è sottoposta la struttura, che in questo caso dovranno essere nulli per T e M.

Posso inoltre, attraverso una tabella, che verrà poi esportata in Excel, ottenere i diversi valori di sforzo assiale, di trazione o compressione, sulle diverse aste.

Esportata la tabella, contrassegnati i valori delle aste diagonali (in rosso), posso eliminare i duplicati, e procedere con il dimensionamento delle aste, attraverso l’utilizzo di un ulteriore foglio di calcolo Excel, in cui dividiamo le aste tese (valori positivi) da quelle compresse (valori negativi).

Trazione
Per dimensionare le aste a trazione, aggiungo i valori di N di trazione al foglio di calcolo Excel, le caratteristiche dell’acciaio scelto (fyk = 235 MPa), ed il coefficiente  γ_m = 1,05, e ottengo per ogni asta una area minima. In base a questo valore posso dimensionare le aste, che dovranno avere una area maggiore del valore ottenuto.

Compressione
Per dimensionare le aste a compressione, invece, aggiungo i valori di N a compressione al foglio di calcolo Excel, le caratteristiche dell’acciaio scelto (fyk = 235 MPa), il coefficiente  γ_m = 1,05, ed ottengo nel modo precedente una area minima per ogni asta.
Poiché per la compressione dobbiamo considerare anche il fenomeno di instabilità, bisogna aggiungere anche i valori del modulo di elasticità dell’acciaio, E = 210000 MPa, e di un coefficiente che dipende dai vincoli delle aste, beta = 1.

Ottengo, attraverso questi dati, tre diversi valori, Lambda, Rho_min e I_min, necessari per il dimensionamento delle aste. I profilati scelti dovranno infatti soddisfare tutti e tre questi valori.

La prima esercitazione prevede il dimensionamento della trave più sollecitata del solaio di carpenteria in tre diverse tecnologie: legno, acciaio e cemento armato.

Solaio in legno

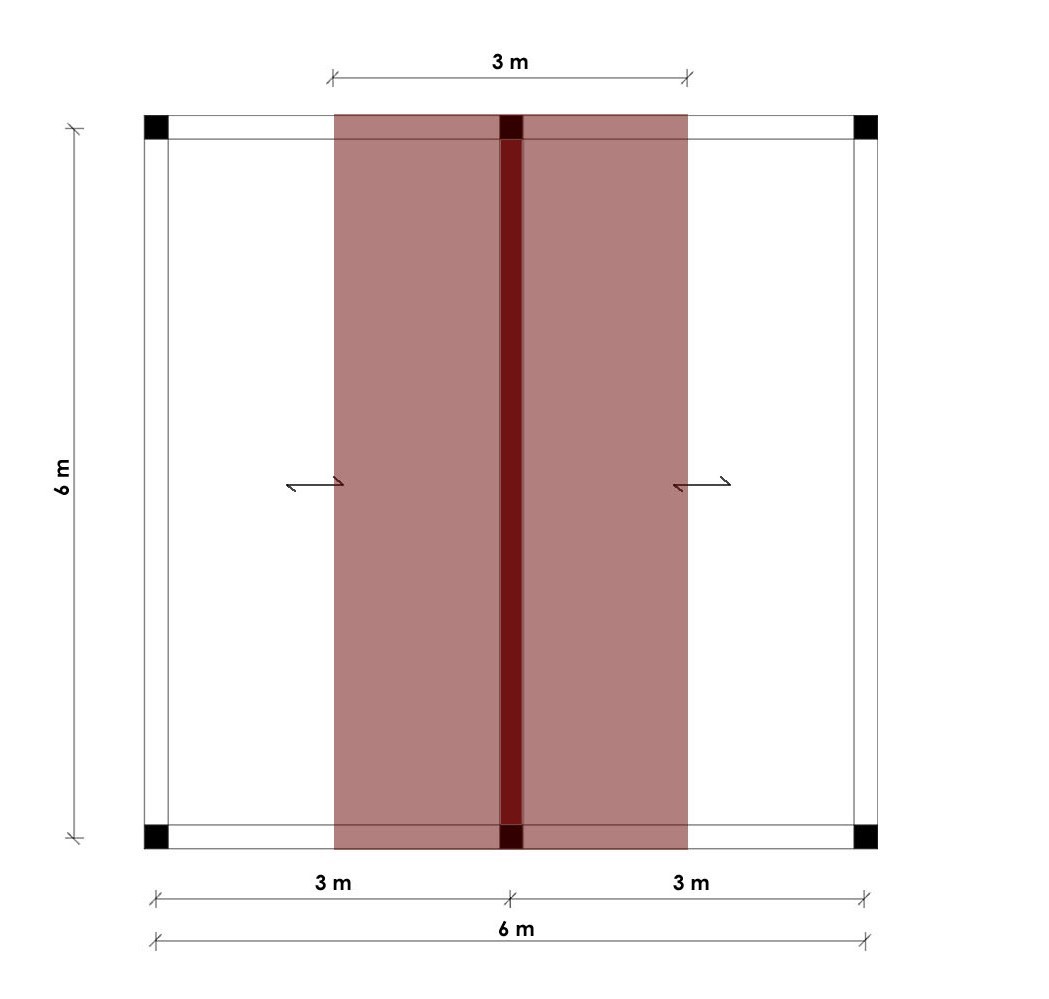
In questo caso la trave maggiormente sollecitata è la trave centrale, che presenta una luce di 6m e un interasse di 3m.

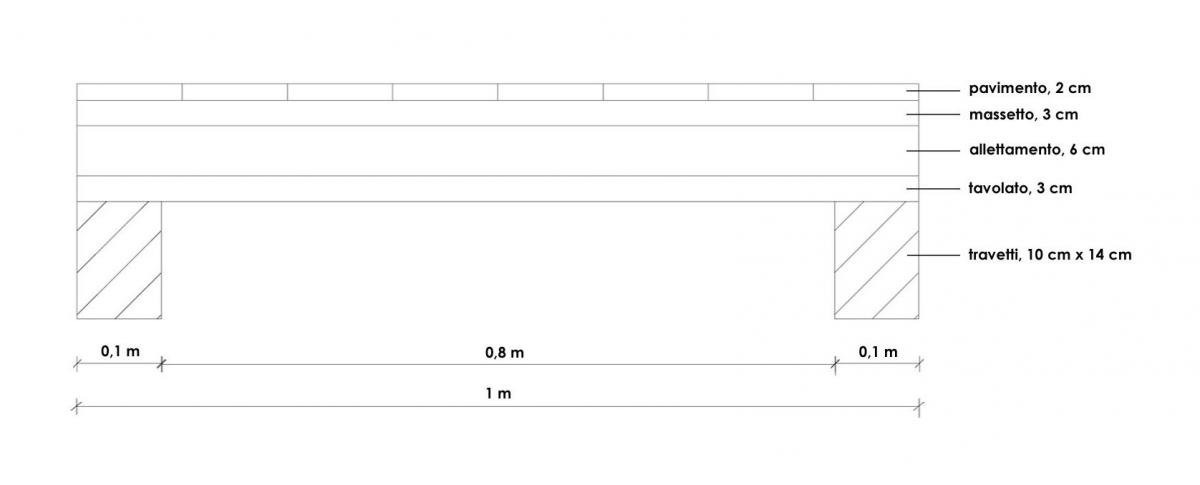
Il solaio preso in considerazione è composto da:
- Pavimento, 2 cm, con peso specifico di 40 kg/mq (=0,4 kN/mq)
- Massetto, 3 cm, con peso specifico di 1900 kg/mc (=19 kN/mc)
- Allettamento, 6 cm, con peso specifico di 1400 kg/mc (=14 kN/mc)
- Tavolato, 3 cm, con peso specifico di 530 kg/mc (=5,3 kN/mc)
- Travetti, 14 cm x 10 cm, con peso specifico di 530 kg/mc (=5,3 kN/mc)

Calcoliamo i diversi carichi agenti sul solaio.

Carico strutturale, qs:

- Travetti: 2 [(5,3 kN/mc)] [(0,14 m) (0,1 m) (1 m)] / 1 mq = 0,15 kN/mq

- Tavolato: [(5,3 kN/mc) (0,03 mc)] / 1 mq = 0,16 kN/mq

Qs = 0,15 kN/mq + 0,16 kN/mq = 0,31 kN/mq

Carico permanente, qp:

- Allettamento: [(14 kN/mc) (0,06 mc)] / 1 mq = 0,84 kN/mq

- Massetto: [(19 kN/mc) (0,03 mc)] / 1 mq = 0,57 kN/mq

- Pavimento: 0,4 kN/mq

- Impianti: 0,5 kN/mq

- Tramezzi: 1 kN/mq

Qp = 0,84 kN/mq + 0,57 kN/mq + 0,4 kN/mq + 1,5 kN/mq = 3,31 kN/mq

Carico accidentale, qa:

Considerando un edificio ad uso residenziale, Qa = 2 kN/mq

Inserendo i valori ottenuti  nel foglio di calcolo excel, otteniamo il valore del carico ultimo, ottenuto moltiplicando i diversi carichi agenti per i rispettivi coefficienti di sicurezza.

Ottenuto il valore del carico ultimo possiamo inoltre trovare il valore del momento massimo, che per una trave appoggiata-appoggiata, di lunghezza l e sottoposta a carica q, equivale a  ql²/8.

Per il progetto di questa trave scegliamo un legno lamellare GL24H, con resistenza a flessione caratteristica fm,k = 24 MPa, e scegliamo come coefficiente di durata del carico kmod = 0,8 e come  coefficiente parziale di sicurezza del materiale γ m = 1,45.
Con l’utilizzo di questi dati è possibile calcolare la tensione ammissibile di progetto fd.
Impostando in seguito la base della trave da calcolare, ci viene fornita l’altezza minima della stessa.

Scegliendo quindi una base di 30 cm otteniamo un’altezza minima di circa 41 cm.
Essendo questo valore il valore minimo dell’altezza della trave, scegliamo un’altezza di 50 cm, ottenendo una trave di sezione 30cm x 50 cm.

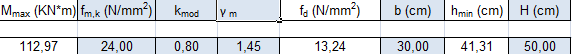
Non avendo considerato il peso stesso della trave, andrebbe verificato che sommando questo peso ai carichi già agenti sulla trave, questa stessa fosse verificata.

Solaio in acciaio

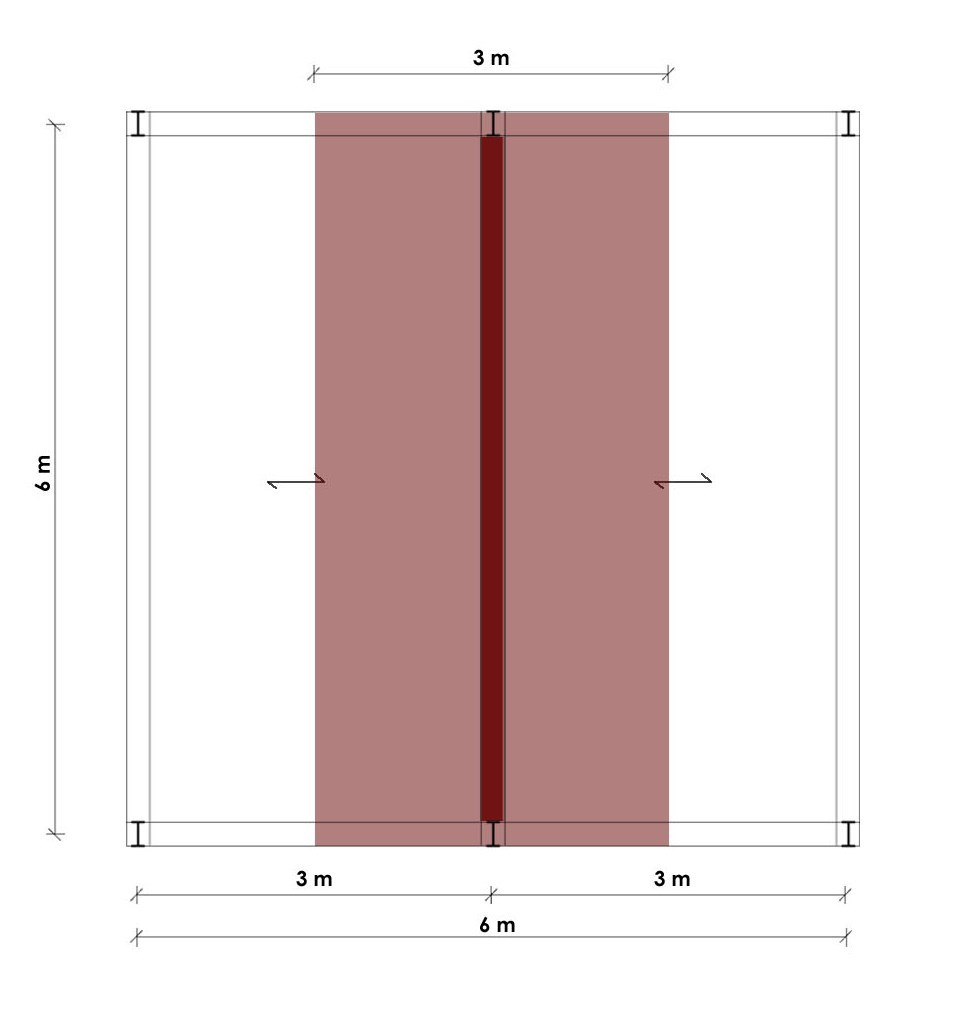
In questo caso la trave maggiormente sollecitata è la trave centrale, che presenta una luce di 6m e un interasse di 3m.

Il solaio preso in considerazione è composto da:
- Pavimento, 2 cm, con peso specifico di 40 kg/mq (=0,4 kN/mq)
- Massetto, 3 cm, con peso specifico di 1900 kg/mc (=19 kN/mc)
- Isolante, 4 cm, con peso specifico di 0,2 kN/mc
- Getto in calcestruzzo e lamiera grecata, 10 cm, con peso specifico di 21 kN/mc
- IPE 200, 20 cm x 10 cm, area di 28,5 cm2, con peso specifico di 78,5 kN/mc

Calcoliamo i diversi carichi agenti sul solaio.

Carico strutturale, qs:

- IPE 200: 2 [(78,5 kN/mc)] [(0,00285 mq)( 1 m)] / 1 mq = 0,45 kN/mq

- Getto in calcestruzzo e lamiera grecata: [(21 kN/mc) (0,075 mc)] / 1 mq = 1,86 kN/mq

Qs = 0,45 kN/mq + 1,86 kN/mq = 2,31 kN/mq

Carico permanente, qp:

- Isolante: [(0,2 kN/mc) (0,04 mc)] / 1 mq = 0,008 kN/mq

- Massetto: [(19 kN/mc) (0,03 mc)] / 1 mq = 0,57 kN/mq

- Pavimento: 0,4 kN/mq

- Impianti: 0,5 kN/mq

- Tramezzi: 1 kN/mq

Qp = 0,008 kN/mq + 0,57 kN/mq + 0,4 kN/mq + 1,5 kN/mq  = 2,55 kN/mq

Carico accidentale, qa:

Considerando un edificio ad uso residenziale, Qa = 2 kN/mq

Inserendo i valori ottenuti  nel foglio di calcolo excel, otteniamo il valore del carico ultimo, ottenuto moltiplicando i diversi carichi agenti per i rispettivi coefficienti di sicurezza.

Ottenuto il valore del carico ultimo possiamo inoltre trovare il valore del momento massimo, che per una trave appoggiata-appoggiata, di lunghezza l e sottoposta a carica q, equivale a  ql²/8.

Per il progetto di questa trave scegliamo un acciaio S235 con resistenza a flessione caratteristica
fy,k = 235 MPa.

Con l’utilizzo di questi dati è possibile calcolare la tensione ammissibile di progetto fd, e il modulo di resistenza Wx minimo, di circa 590 cm3.

Scegliamo quindi una trave IPE 330, con modulo di resistenza Wx pari a 713,10 cm3.

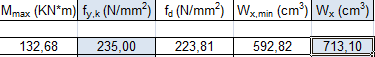
Non avendo considerato il peso stesso della trave, andrebbe verificato che sommando questo peso ai carichi già agenti sulla trave, questa stessa fosse verificata.

Solaio in cemento armato

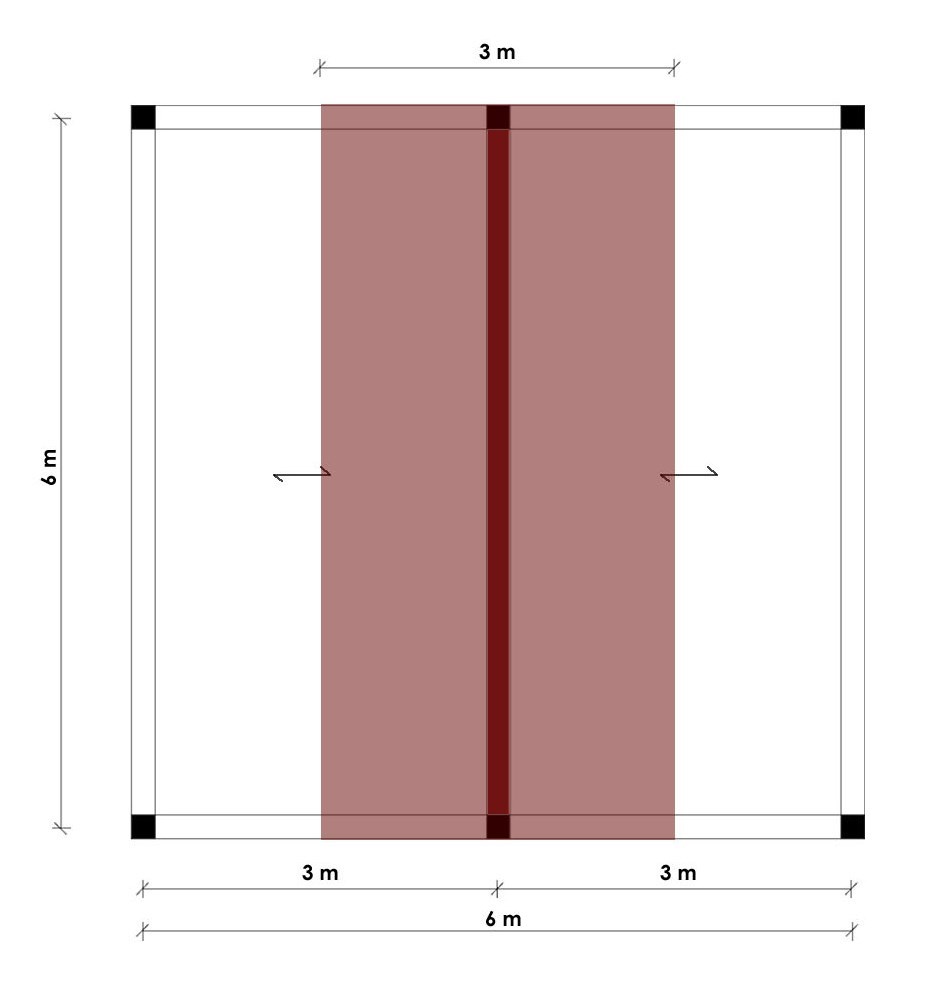
In questo caso la trave maggiormente sollecitata è la trave centrale, che presenta una luce di 6m e un interasse di 3m.

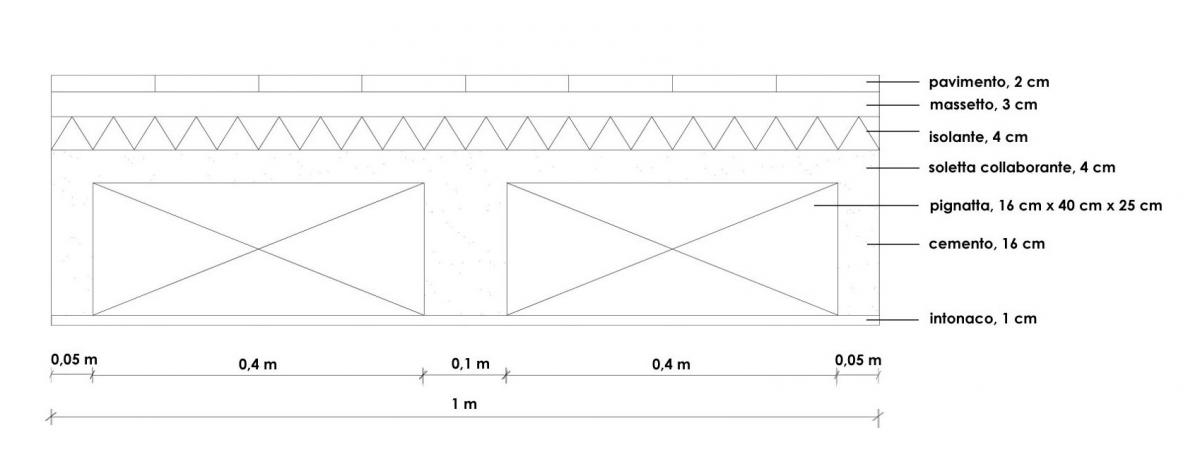
Il solaio preso in considerazione è composto da:
- Pavimento, 2 cm, con peso specifico di 40 kg/mq (=0,4 kN/mq)
- Massetto, 3 cm, con peso specifico di 1900 kg/mc (=19 kN/mc)
- Isolante, 4 cm, con peso specifico di 0,2 kN/mc
- Getto in calcestruzzo, 20 cm (16 cm + 4 cm), con peso specifico di 24 kN/mc
- Pignatta, 16 cm x 40 cm x 25 cm, con peso di 9,1 kg (= 0,091 kN)
-Intonaco, 1 cm, con peso specifico di 18 kN/mc

Calcoliamo i diversi carichi agenti sul solaio.

Carico strutturale, qs:

- Getto in calcestruzzo: [(24 kN/mc) (0,04 m) (1 m) (1 m)] / 1 mq = 0,96 kN/mq

- Getto in calcestruzzo: [(24 kN/mc) (0,16 m) (0,10 m) (1 m)] / 1 mq = 0,77 kN/mq

- Pignatte: 8 (0,091 kN) / 1 mq = 0,73 kN/mq

Qs = 0,96 kN/mq + 0,77 kN/mq + 0,73 = 2,46 kN/mq

Carico permanente, qp:

- Isolante: [(0,2 kN/mc) (0,04 mc)] / 1 mq = 0,008 kN/mq

- Massetto: [(19 kN/mc) (0,03 mc)] / 1 mq = 0,57 kN/mq

- Pavimento: 0,4 kN/mq

- Impianti: 0,5 kN/mq

- Tramezzi: 1 kN/mq

- Intonaco: [(18 kN/mc) (0,01 mc)] / 1 mq = 0,18 kN/mq

Qp = 0,008 kN/mq + 0,57 kN/mq + 0,4 kN/mq + 1,5 kN/mq + 0,18 kN/mq  = 2,66 kN/mq

Carico accidentale, qa:

Considerando un edificio ad uso residenziale, Qa = 2 kN/mq

Inserendo i valori ottenuti  nel foglio di calcolo excel, otteniamo il valore del carico ultimo, ottenuto moltiplicando i diversi carichi agenti per i rispettivi coefficienti di sicurezza.

Ottenuto il valore del carico ultimo possiamo inoltre trovare il valore del momento massimo, che per una trave appoggiata-appoggiata, di lunghezza l e sottoposta a carica q, equivale a  ql²/8.

Per il progetto di questa trave scegliamo per l’armatura un acciaio con resistenza a flessione caratteristica fy,k = 450 MPa, e un calcestruzzo con resistenza fc,k = 60 MPa.

Con l’utilizzo di questi dati è possibile calcolare le tensioni di progetto fyd e fcd, rispettivamente dell'acciaio e del cemento.
Impostando in seguito la base della trave da calcolare e la dimensione del copriferro, ci viene fornita l’altezza utile e l’altezza minima della stessa.

Scegliendo quindi una base di 20 cm e un copriferro di 3 cm, otteniamo un’altezza utile di circa 29 cm, e quindi una altezza minima di circa 32 cm.
Essendo questo valore il valore minimo dell’altezza della trave, scegliamo un’altezza di 35 cm, ottenendo una trave di sezione 20cm x 35 cm.

Non avendo considerato il peso stesso della trave, va verificato che sommando questo peso ai carichi già agenti sulla trave, questa stessa fosse verificata.

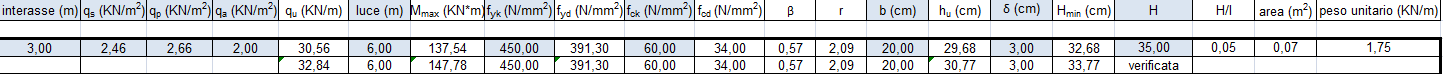
La trave scelta di sezione 20 cm x 35 cm è verificata per il solaio in questione.