Dimensionamento di una trave a sbalzo

Per la seconda esercitazione abbiamo dimensionato una trave a sbalzo.

La trave a sbalzo apparterrà ad un solaio di nostra scelta. Quello preso in considerazione è costituito in modo tale che la trave a sbalzo più sollecitata è quella centrale, con le seguenti caratteristiche:

Interasse: 3,5 m

luce: 2 m

Da qui proseguiremo quindi con il dimensionamento della trave nei confronti delle tre tipologie costruttive: legno, calcestruzzo armato e acciaio

Solaio in legno

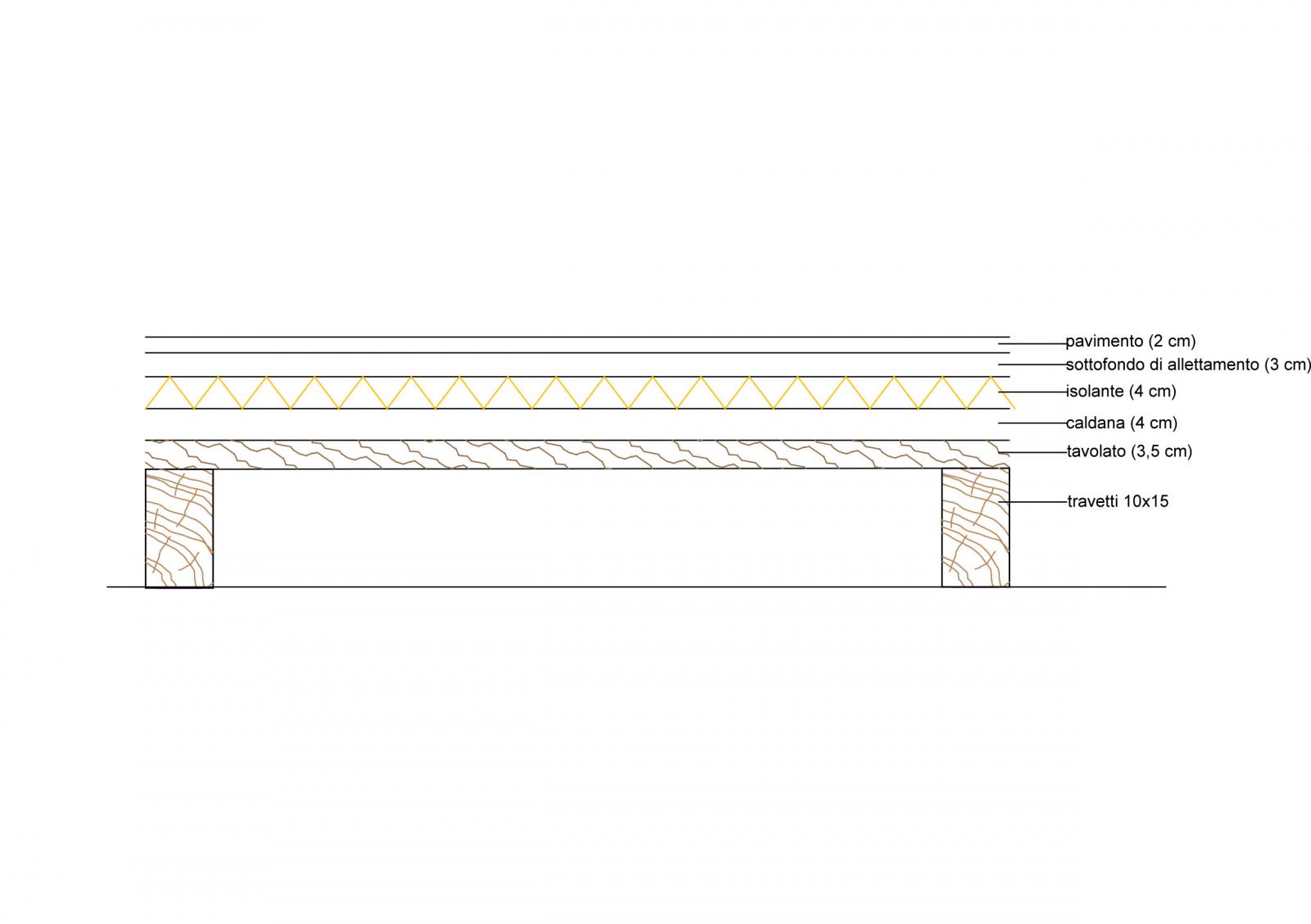La prima tecnologia analizzata è quella di un solaio in legno, costiuito dai seguenti elementi:

Pavimento: 7,5 KN/Mc (2 cm)

sottofondo di allettamento: 18 KN/Mc (3 cm)

isolante: 0,2 KN/Mc (4 cm)

caldana: 25 KN/Mc (4 cm)

tavolato: 6 KN/Mc (3,5 cm)

travetti: 5,3 KN/Mc travetti 10x15

Calcolo ora il carico strutturale, il carico permanente e il carico accidentale.

pavimento:      7,5 x 1 x 1 x 0,02 = 0,15 KN/mq

sottofondo:     18 x 1 x 1 x 0,03 = 0,54 KN/mq

isolante:          0,2 x 1 x 1 x 0,04 = 0,008 KN/mq

caldana:          25 x 1 x 1 x 0,04 = 1 KN/mq

tavolato:          3,5 x 1 x 1 x 0,035 = 0,122 KN/mq

travetti:            3,5 x 10 x 10 x 2 = 0, 106 KN/mq

qs: 1 + 0,106 + 0,122= 1,22 KN/mq

qp: 0,36 + 0,54 + 0,008 + 0,5 + 1 = 2,19 KN/mq

qa: 2 KN/mq 

Prendendo quindi in considerazione la misura di interasse della trave, il valore dei carichi strutturali, permanenti e accidentali otterremo il carico qu= 1,3qs + 1,5qp + 1,5qa = 27,5 KN/m

Inserisco poi la luce della trave a sbalzo.

Calcolerò così il momento max Mmax: ql^2/2 = 55 KNm

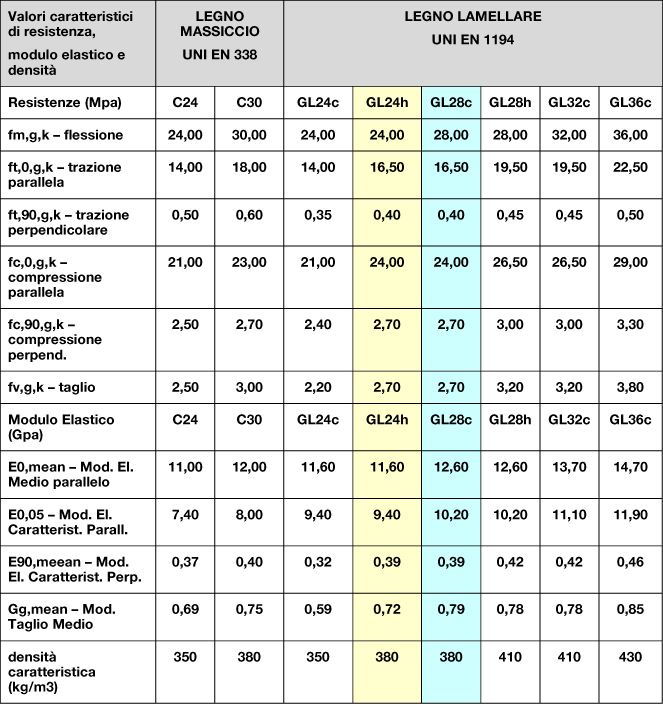
Scegliamo di utilizzare un legno massiccio C24 con resistenza caratteristica fmk: 24 KN/mmq , coeff. di riduzione kmod:0,5 . Introduciamo poi un ulteriore fattore di riduzione ym= 1,5 da normativa.

Fissando una base di 30 cm otterremo una altezza min di hmin= ( 6 X Mmax x 1000/ b x fd,C)^0,5 = 38,56

La nostra sarà quindi una trave in legno C24 30 x 40.

Calcoleremo poi il carico di esercizio qe: (qs + qp + 0,5qa)x interasse= 15 KN/m e da questo sarà valutato l'abbassamento max Vmax= qe x 10 x ( l x 100)^4/8 x E x Ix = 0, 46 cm

Solaio in acciaio

Il solaio in acciaio sarà costiutito dai seguenti elementi:

pavimento: 7,5 KN/mc (2 cm)

sottofondo: 18 KN/mc ( 30 cm)

isolante: 0,2 KN/mc ( 40 cm)

soletta: 2,5 KN/mq ( 15 cm di cui lamiera grecata 7,5 cm)

travetti: 78,5 KN/mc  IPE 100

Calcolo quindi i carichi agenti

qs:  (2,5 x 1 x 1) + (78,5 x 0,001032 x 2) = 2,66 KN/mq

qp: (0,2 x 0,04 x 1 x 1) + (18 x 0,03 x 1 x 1) + (18 x 0,02 x 1 x 1) + 0,5 + 1 = 2,4 KN/mq

qa: 2 KN/mq

Calocleremo quindi, ugualmente a prima, il carico ultimo qu: 35,2 KN/m e il momento massimo Mmax: 70,40 KNm

Utilizzeremo un acciaio S235 con resistenza caratteristica fyk:235 N/mmq e fyd: fyk/1,05= 223,81 N/mmq

Otterremo quindi la resistenza elastica Wx: Mmax/fyd= 314,58 cm^3

Il profilato da noi scelto sarà quello corrispondente al valore di Wx subito maggiore ossia Wx=428,9 ossia una IPE 270

Possiamo ora inserire il peso e il momento d'inerzia corrispondenti

Calcoleremo il carico di esercizio qe: ( qs + qp + 0,5qa) x interasse + peso= 21, 57 KN/m

Infine prendendo in considerazione il modulo elastico E=210000 N/mmq calcoliamo l'abbassamento massimo

Vmax= qe x 10 x (l x 100)^4 / 8 x E x Ix

Solaio in laterocemento

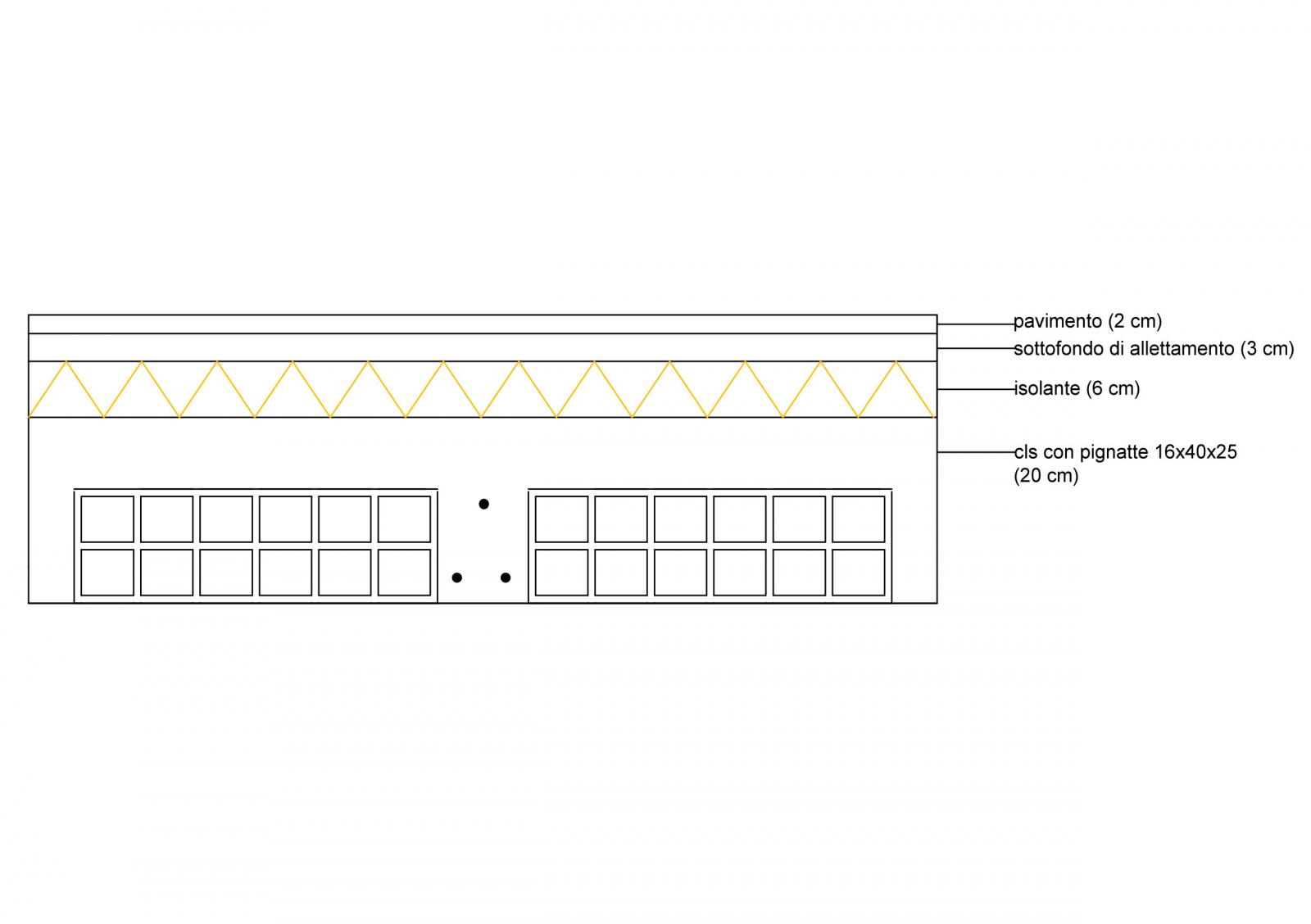
Formato dai seguenti elementi:

pavimento: 40 kg/mq ( 2 cm)

massetto: 19 KN/mc ( 3 cm)

isolante: 20 kg/ mq ( 6 cm)

soletta cls: 24 KN/mc (16 cm) con pignatte 16 x 40 x 25 da 9,1 kg/mq

Calcoliamo quindi i carichi agenti

qs: (24 x 1 x 1 0,04) + (24 x 2 x 0,16 x 0,1 x 1) + (9,1 x 8)= 2, 46 KN/mq

qp: 0,4 + (19 x 0,003 x 1 x 1) + (0,2 x 0,06 x 1 x 1) + (18 x 0,01 x 1 x 1)= 1,162 KN/mq

qa: 2 KN/mq

Calcoliamo come le altre volte il carico ultimo e il momento max.

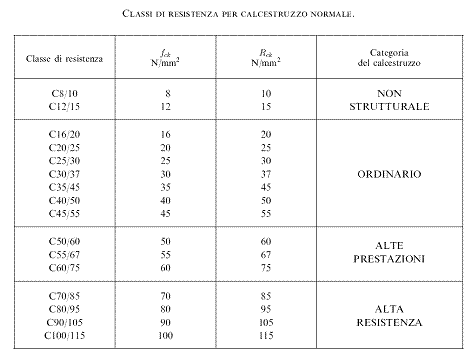
Utilizzeremo per la nostra sezione un acciaio S450 con resistenza caratteristica fyk=450 N/mmq e fyd= 391,3 N/mmq e calcestruzzo C30 con resistenza caratteristica fck: 30 N/mmq e fcd: 0,86 x fck/1,5= 17 N/mmq

scegliendo una base del nostro profilato b= 30 cm otterremo una altezza utile hu: 25,22 a cui sommeremo il copreiferro da noi scelto pari a 5 cm, ottenendo così una altezza minima Hmin=31,22 cm

Sceglieremo quindi di utilizzare una sezione 30 x 50

Inserendo quindi il modulo elastico E otterremo il suo abbassamento massimo ossia Vmax=0,06 cm