ESERCITAZIONE 3: Deformabilità di una trave a sbalzo (mensola)

Questa terza esercitazione consiste nel dimensionare una trave a sbalzo in legno, in acciaio

e in c.a., in modo che alla fine il valore dello spostamento massimo v_max  soddisfi la

disequazione l / v_max > 250.

La prima differenza rispetto alla prima esercitazione è nel valore del momento massimo:

infatti lo schema statico di riferimento non è più quello della trave doppiamente appoggiata

(M_max = q_ul²/8) ma quello della mensola (M_max = q_ul²/2). Inoltre per questa esercitazione

bisogna prendere in considerazione il valore del modulo elastico E proprio di ogni materiale e

del momento di inerzia I_x, che servono a calcolare lo spostamento massimo.

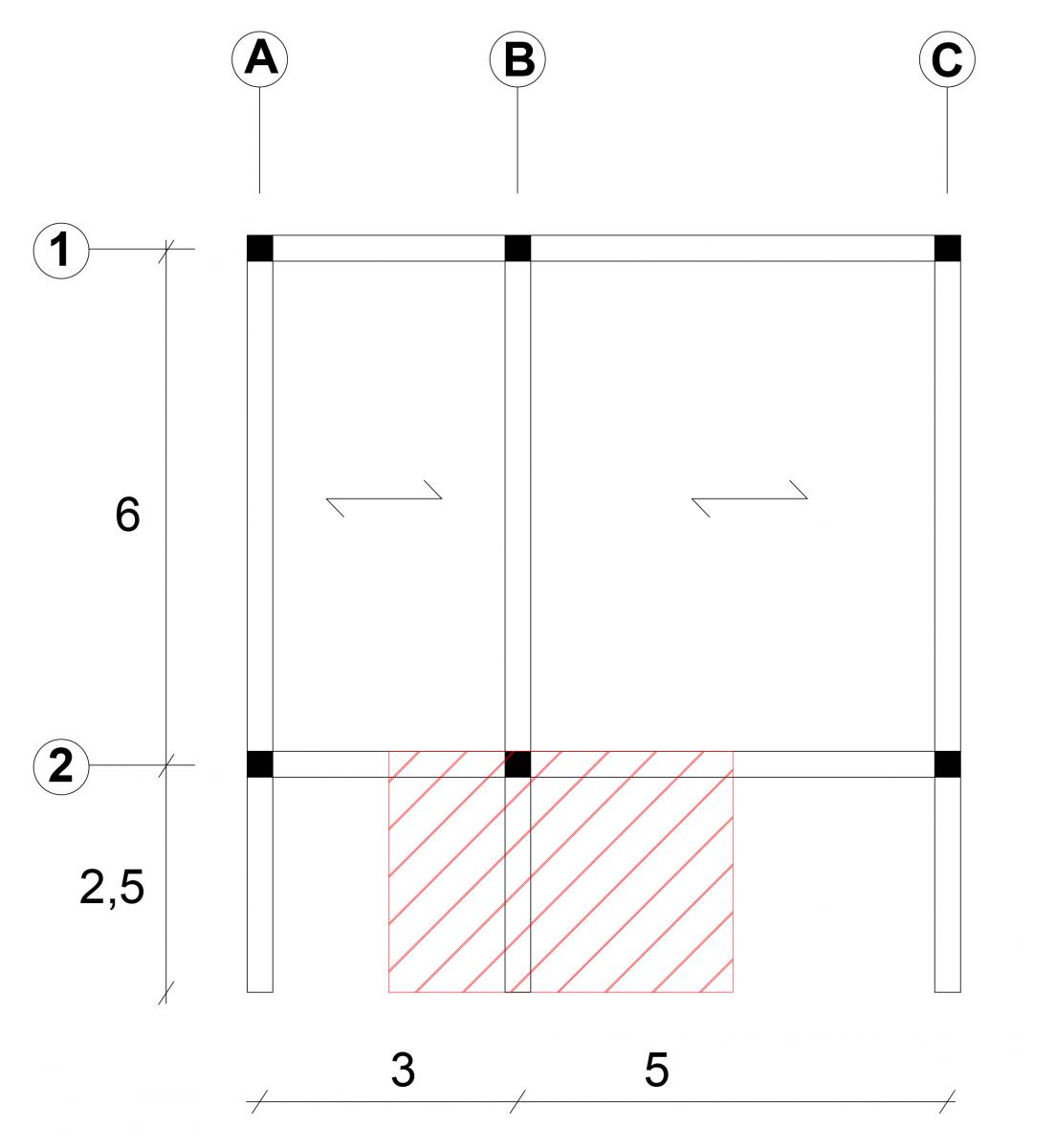
Prendo in esame la trave maggiormente sollecitata, ovvero la trave B.

SOLAIO IN LEGNO

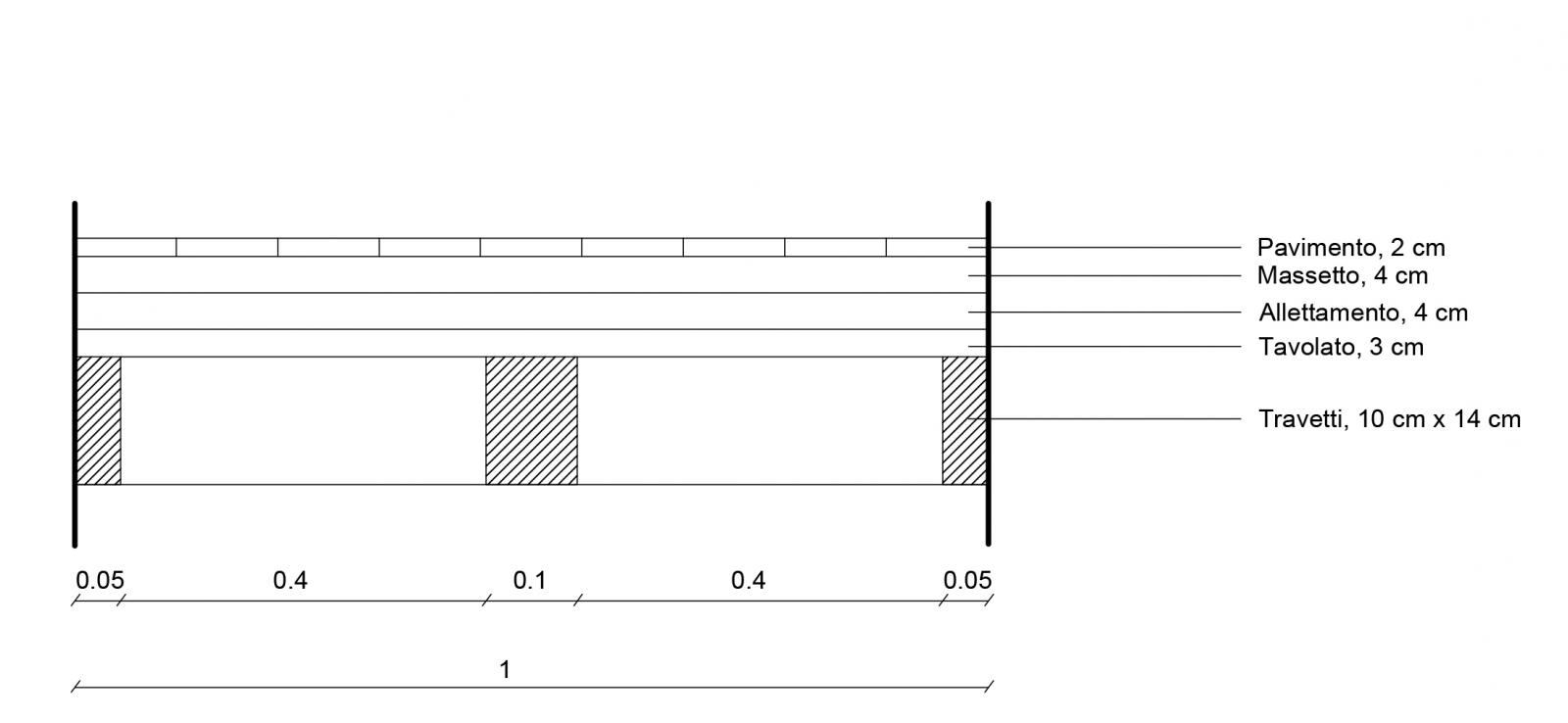
La sezione del solaio è la stessa di quella usata nella ESERCITAZIONE 1, per questo motivo

ho già i valori q_s = 0,33 KN/mq      q_p = 3, 22 KN/mq       q_a = 2 KN/mq, che mi

determinano  q_u = 33,036 KN/mq.

Scelgo un legno lamellare GL24H che ha f_m,k = 24,00 MPa, k_mod = 0,80  e y_m = 1,45.

Imposto come base 25 cm e, siccome viene determinata un'altezza minima di 43,26 cm,

scelgo un altezza di 45 cm. Inserisco poi il modulo elastico del materiale  E = 8000 N/mm²

e il momento di inerzia I_x = 189844 cm⁴.

A questo punto il sistema calcola lo spostamento massimo e siccome

 l / v_max = 427,25 > 250 la trave 25 cm x 45 cm risulta verificata. 

SOLAIO IN ACCIAIO

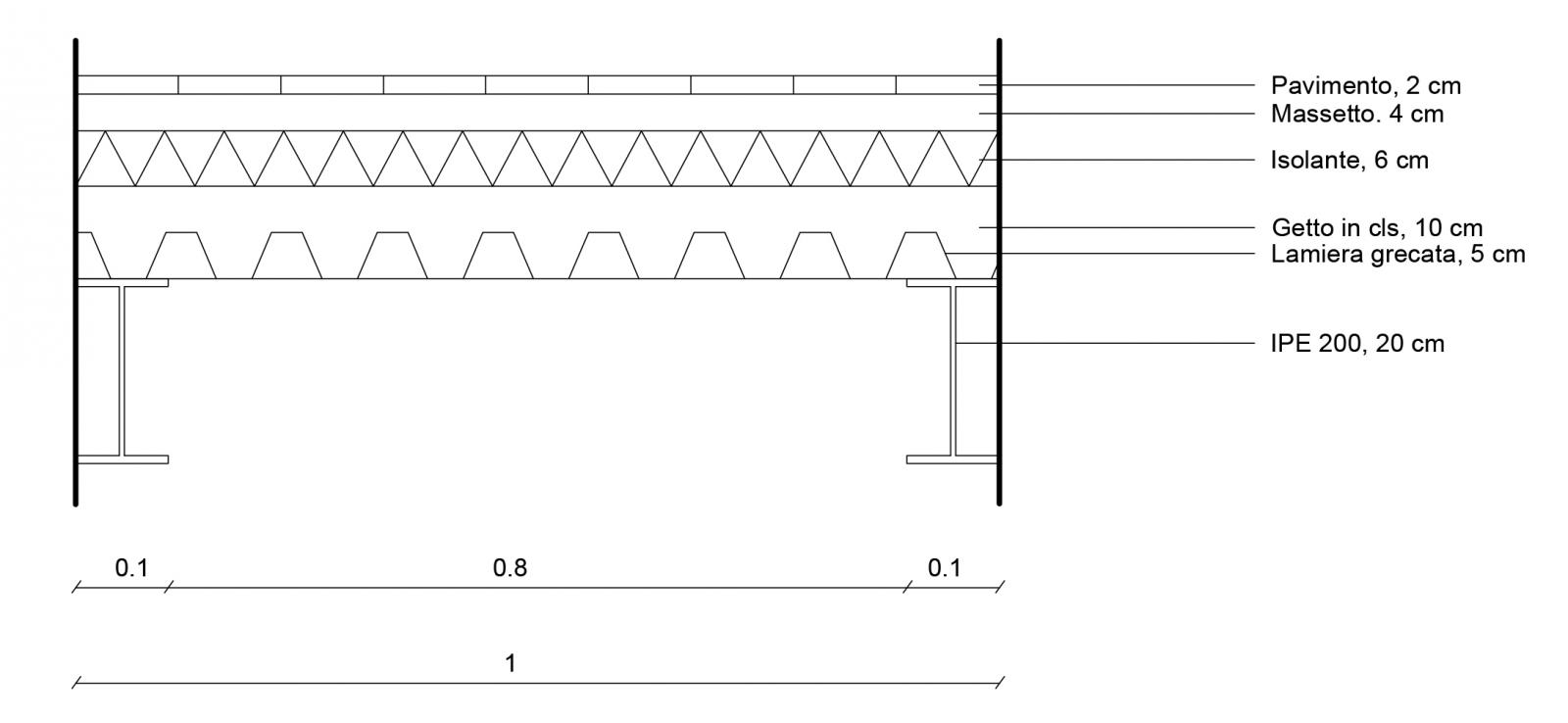
Anche per il solaio in acciaio ho già i valori q_s = 2,31 KN/mq      q_p = 2,672 KN/mq    

q_a = 2 KN/mq, che mi determinano q_u = 40,044 KN/mq.

Scelgo poi un acciaio S235 che ha f_y,k = 235 N/mm².

Siccome W_x,min = 559,13 cm³ , scelgo un profilato IPE 330 (W_x = 713, 1 cm³) e inserisco il

suo I_x = 11770 cm⁴ e il suo peso P = 0,49 KN/m. 

Inserendo poi il modulo elastico dell'acciaio E = 210000 N/mm², il sistema calcola lo

spostamento massimo e siccome l / v_max = 518,269 > 250 la trave scelta risulta verificata.

SOLAIO IN C.A.

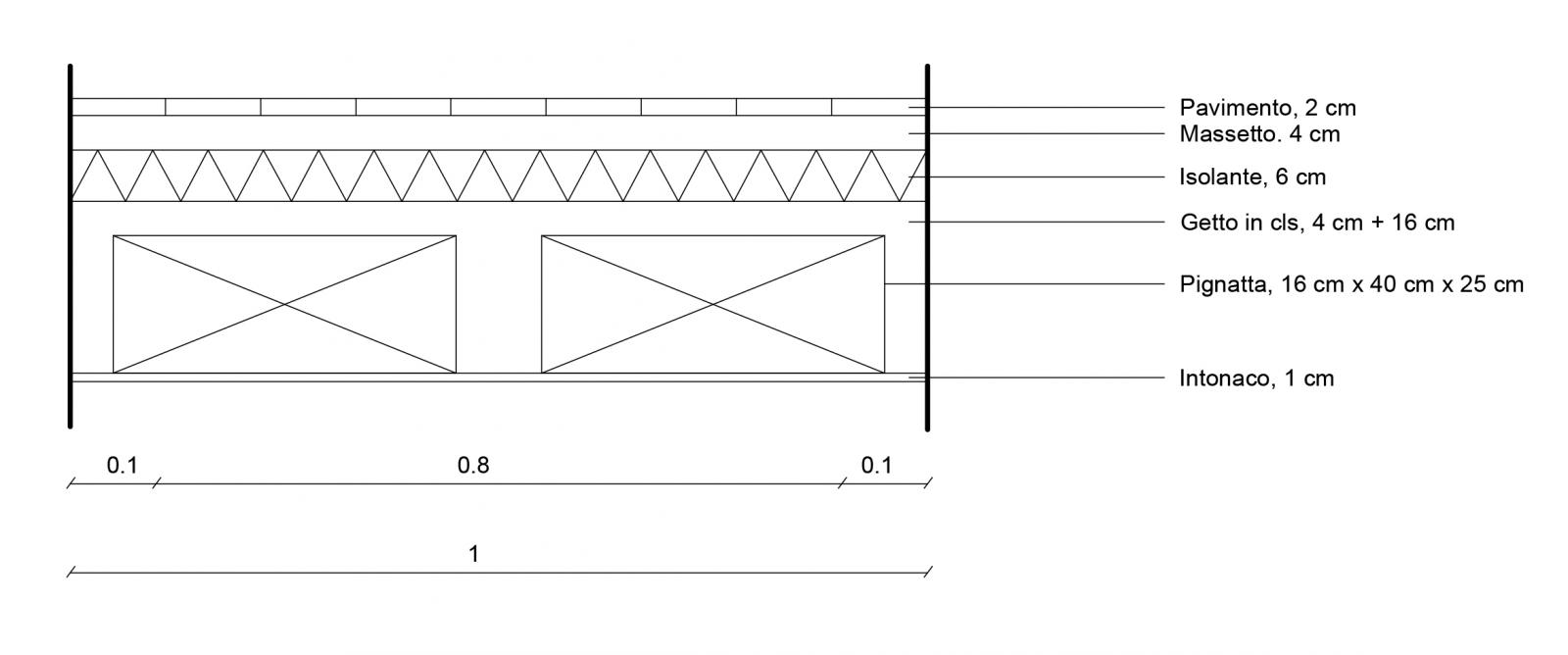
Anche per il solaio in c.a. ho già i valori q_s = 2,46 KN/mq      q_p = 2,852 KN/mq       

q_a = 2 KN/mq, che mi determinano q_u = 41,90 KN/mq.

A seconda dell'acciaio e del cls che scelgo per la trave inserisco f_y,k e f_c,k, che nel mio caso

sono  f_y,k = 450 N/mm²  e  f_c,k  = 60 N/mm². 

Imposto una base di 20 cm e, siccome l'altezza minima viene di 33,96 cm, scelgo un'altezza

di 40 cm.

Il sistema, aggiungendo il peso proprio della trave, calcola un'altezza minima di 33,96 cm e

quindi la trave 20 cm x 40 cm risulta verificata. 

Inserendo poi il modulo elastico E = 21000 N/mm² , il sistema calcola I_x = 106667 cm⁴.

Ne deriva lo spostamento massimo e siccome il rapporto l / v_max = 420,90 > 250 la trave

scelta risulta verificata anche in relazione all'abbassamento.