La quarta esercitazione prevede il dimensionamento , tramite un foglio di calcolo Excel, del
pilastro più sollecitato di un edificio generico a più livelli nelle varie tecnologie : in legno,
acciaio e c.a.
Per quanto riguarda il legno e l'acciaio, il foglio Excel può essere diviso in quattro parti: la
prima riguarda i dati relativi all'area di influenza del pilastro, la seconda mira ad ottenere il
valore dello sforzo normale agente sul pilastro, la terza ci permette di calcolare l'area
minima che la sezione del pilastro dovrà avere per far sì che il materiale non arrivi a rottura e
infine la quarta parte riguarda l'area finale del pilastro e il suo momento di inerzia minimo.
Nel foglio di calcolo relativo al c.a. vi è in più una quinta parte che prende in considerazione il
fatto che il cemento armato, oltre allo sforzo di compressione, è soggetto anche a presso-flessione.
PIANTA PIANO TIPO E SEZIONE DELL'EDIFICIO
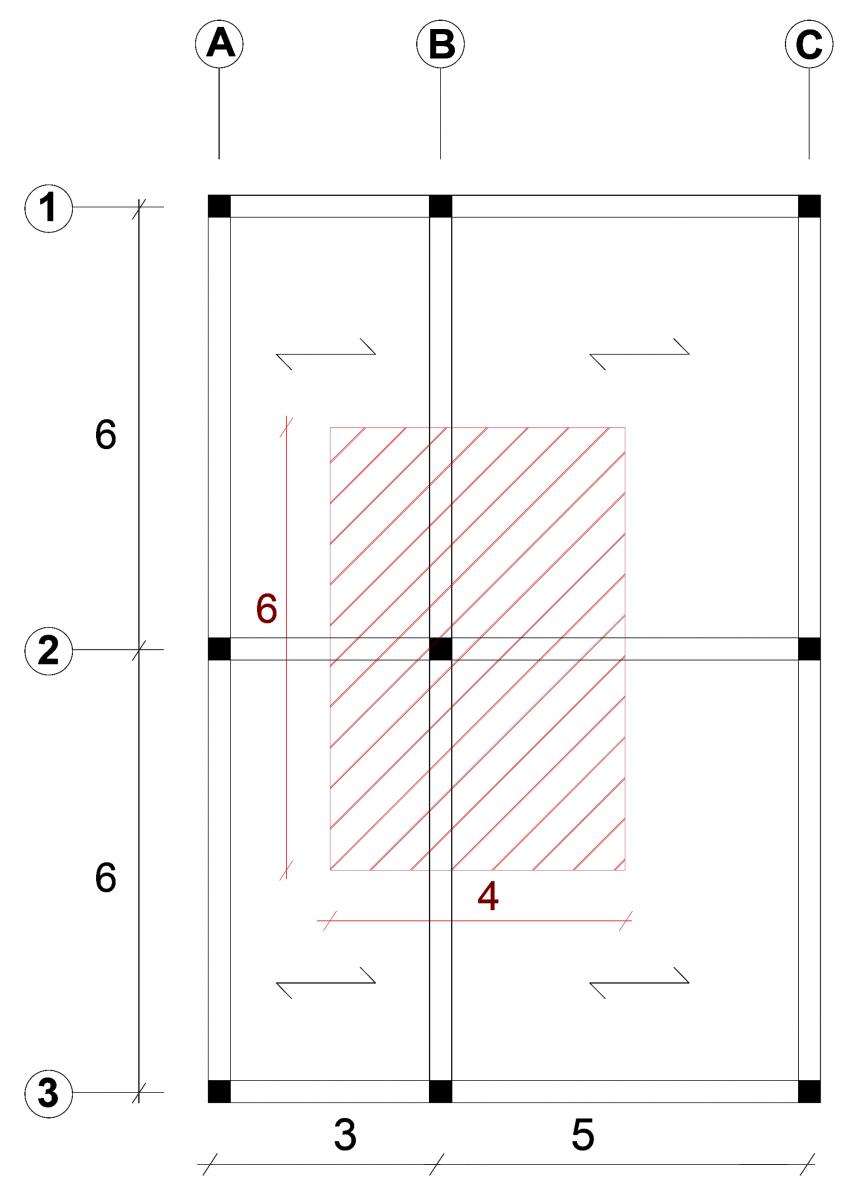
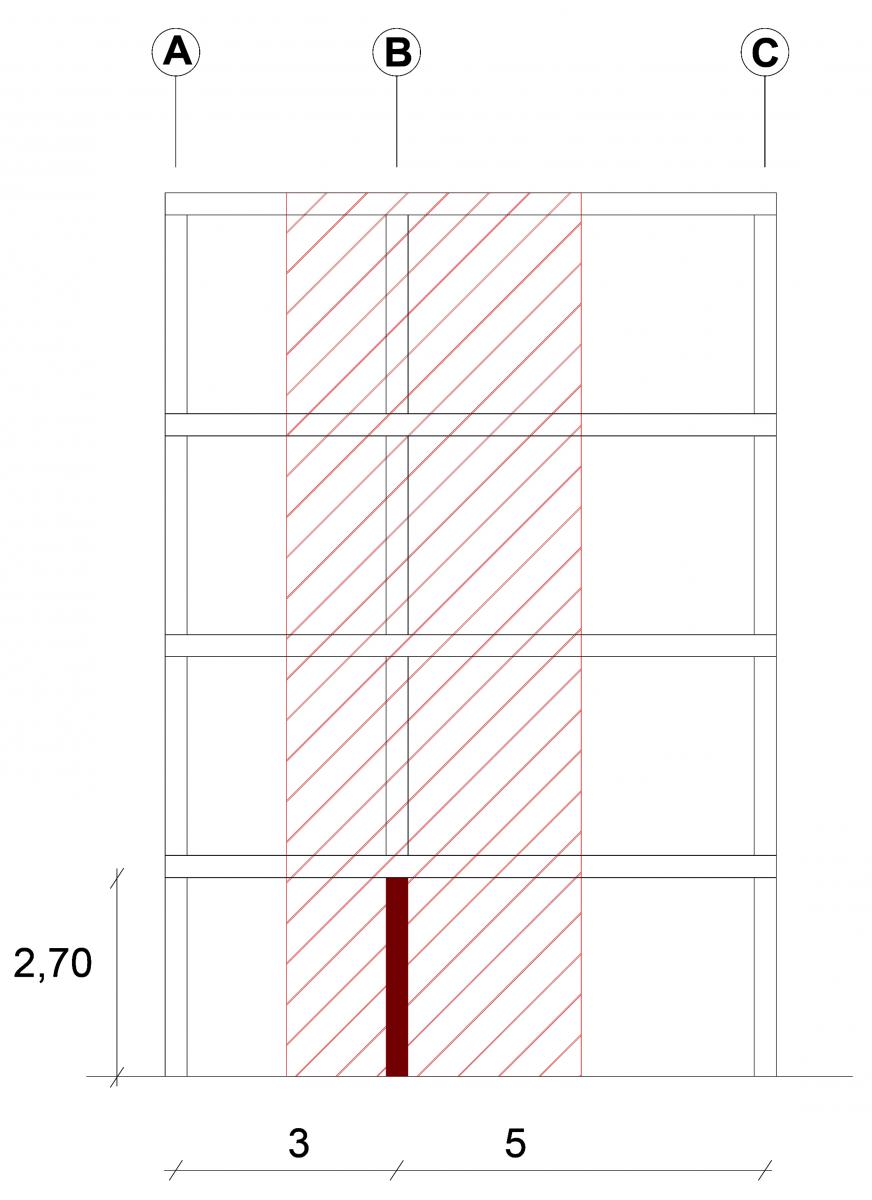
Considerato il seguente impalcato, il pilastro più sollecitato sarà sicuramento il pilastro B2 al
piano terra. Esso ha un'area di influenza di lati 6m x 4m, per un totale di 24m2, e un'altezza di
2,70m.
LEGNO
Per prima cosa inserisco i dati relativi all'area di influenza del pilastro. Poi inserisco il peso
delle travi e il carico del solaio (per i quali faccio riferimento alla prima
esercitazione http://design.rootiers.it/strutture/node/1810) che, insieme
al numero di livelli dell'edificio, contribuiscono a calcolare lo sforzo normale totale agente sul
pilastro.

Come si può vedere dalla tabella, lo sforzo normale è pari a N = 847 kN.
Procedo poi con l'inserimento dei dati relativi alle caratteristiche del materiale, a partire dalla
resistenza, che mi permettono di calcolare l'Area minima che la sezione del pilastro dovrà
avere, il momento di inerzia minimo e il valore massimo sopportato di snellezza.
Questi risultati mi permettono di calcolare la base e l'altezza minima della sezione del
pilastro, in questo caso bmin = 11,55 cm e hmin = 42,67 cm.

Sovradimensionando questi valori, ottengo un pilastro di 15 cm x 45 cm, la cui area finale
Adesign = 675 cm2 > Amin = 640 cm2.
ACCIAIO
Anche nel caso dell'acciaio per prima cosa inserisco i dati relativi all'area di influenza del
pilastro, al peso delle travi e del solaio (ancora una volta faccio riferimento ai risultati della
prima esercitazione http://design.rootiers.it/strutture/node/1810) e al numero di piani
dell'edificio.
Questa volta lo sforzo normale agente sul pilastro risulta pari a N = 983 kN.

Aggiungo poi le informazioni che riguardano le proprietà del materiale, che mi permettono di
calcolare l'area minima che il pilastro dovrà avere, il raggio di inerzia minimo, il momento di
inerzia minimo e il valore di snellezza massimo consentito.
Tenendo conto di questi risultati posso infine scegliere un profilato che soddisfi tutte le
condizioni necessarie.

In questo caso il profilato migliore è un HEA180, con :
Adesign = 45,3 cm2 > Amin = 37,5 cm2
Idesign = 2510 cm4 > Imin = 346 cm4
ρmin = 7,45 cm > ρmin = 3,04 cm.
C.A.
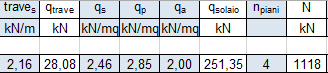
Come per l'acciaio e il legno, anche per il cemento armato come prima cosa inserisco le
informazioni finalizzate al calcolo dello sforzo normale agente sul pilastro, in questo caso pari
a N = 1118 kN.
Passo poi all'inserimento dei dati relativi alle caratteristiche del materiale, che mi permettono
di ottenere la base e l'altezza minima che la sezione del pilastro dovrà avere. In questo caso
bmin = 4,89 cm e hmin = 19,72 cm.
Da notare il valore di β, diverso rispetto ai casi precedenti perchè tiene conto dell'incastro
presente nel nodo del telaio in c.a. (a differenza della cerniera nel caso del legno e
dell'acciaio).

Sovradimensionando i valori della bmin e della hmin, ottengo un pilastro di 25 cm x 50 cm.
La sezione scelta verifica i requisiti richiesti, infatti: σmax = 21,01 Mpa < fcd = 22,7 Mpa.

Commenti recenti