ESERCITAZIONE 5: Ripartizione forza sismica

La quinta esercitazione consiste nel calcolare la ripartizione di una forza orizzontale, come

può essere il sisma o il vento, sui diversi telai che compongono una struttura. 

Prendiamo in considerazione un generico edificio, il cui piano tipo è costituito da telai

shear-type, un particolare tipo di telaio in c.a. che, oltre a trasmettere i carichi verticali a

terra, è capace di svolgere il ruolo di controvento.

STEP 1

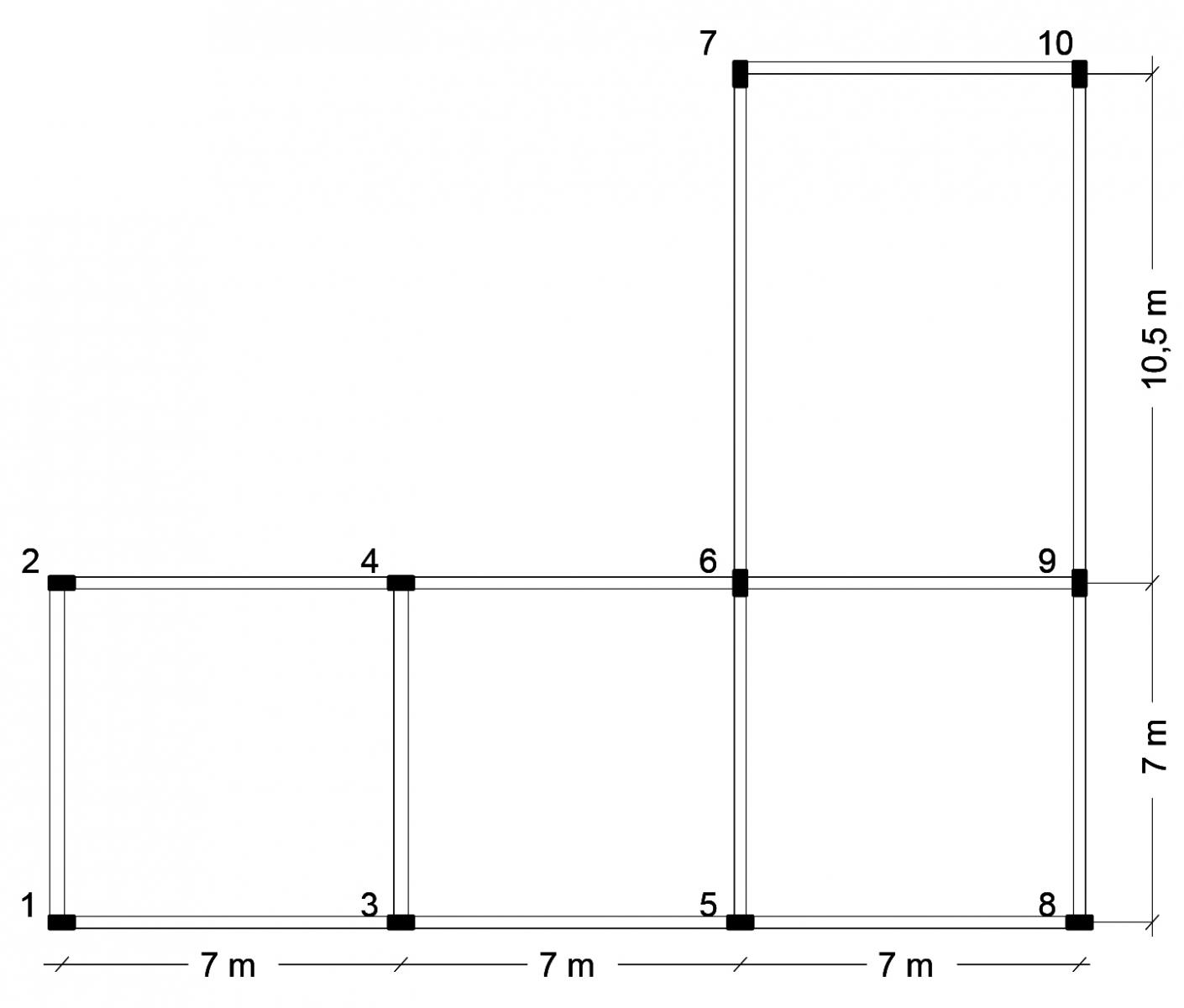
La pianta strutturale dell'edificio preso in considerazione è composta da 7 telai, di cui 4

verticali e 3 orizzontali.

I pilastri hanno sezione 25 cm x 50 cm.

Possiamo dividere i telai in questo modo:

v₁ = pilastri 1 e 2                                        o₁ = pilastri 1, 3, 5 e 8

v₂ = pilastri 3 e 4                                        o₂ = pilastri 2, 4, 6 e 9

v₃ = pilastri 5, 6 e 7                                    o₃ = pilastri 7 e 10

v₄ = pilastri 8, 9 e 10

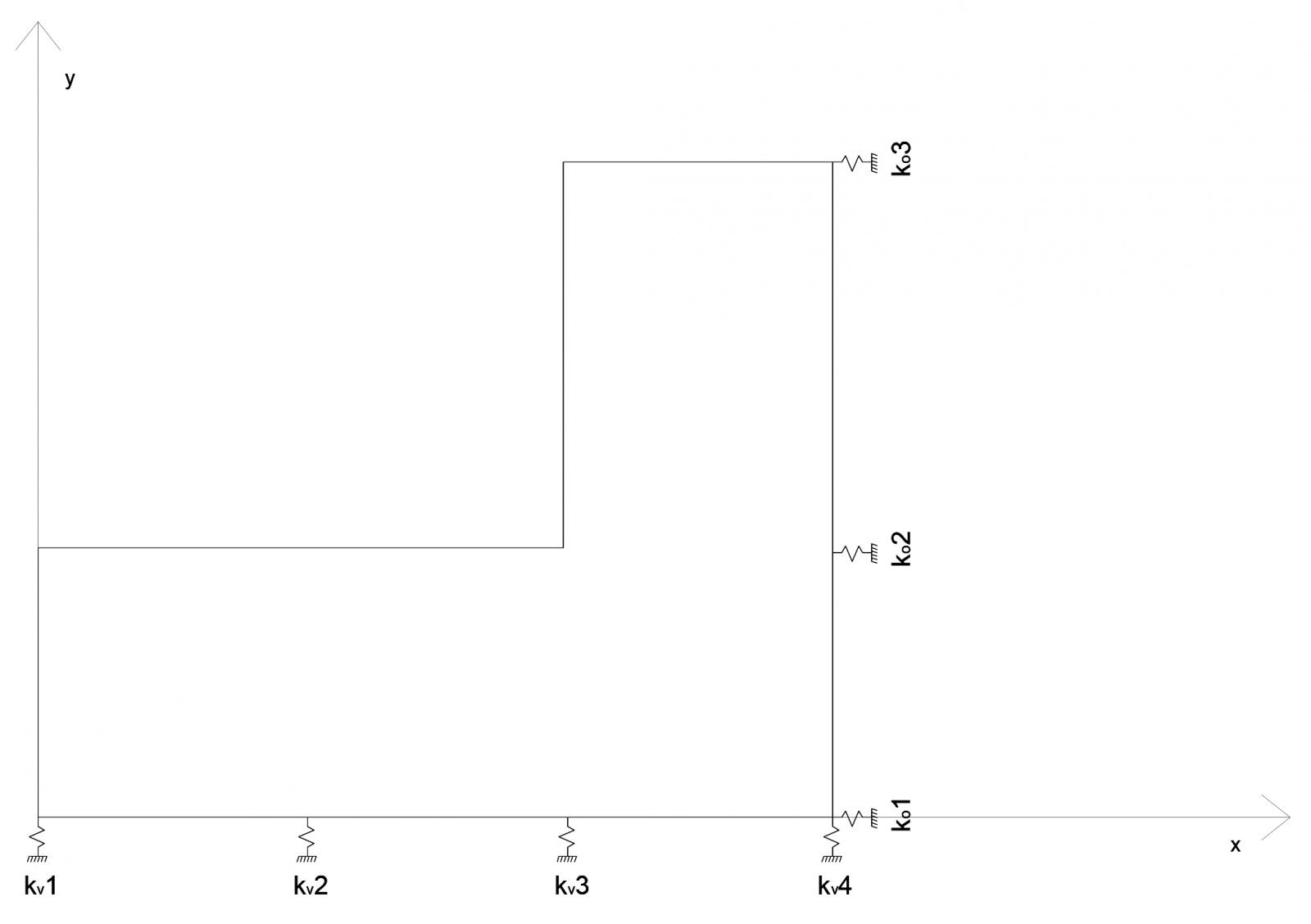
Posso rappresentare in pianta i controventi come molle, ovvero come vincoli elastici. Questi

sono un particolare tipo di vincoli che esercitano una forza reattiva ma allo stesso tempo

subiscono una deformazione. Forza reattiva e deformazione sono direttamente proporzionali. 

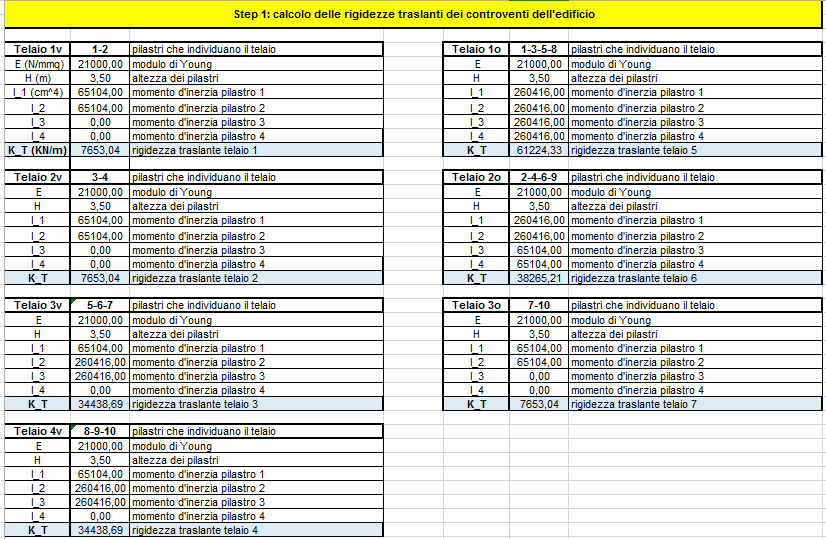
Nella prima parte del foglio Excel mi ricavo la rigidezza traslante di ogni telaio data dalla

formula k = 12 EI/ h³ + 12 EI/ h³.

Bisogna però fare attenzione al momento d'inerzia di ogni pilastro, diverso a seconda del loro

orientamento.

I due valori possibili sono 65.104 cm⁴ e 260.416 cm⁴.

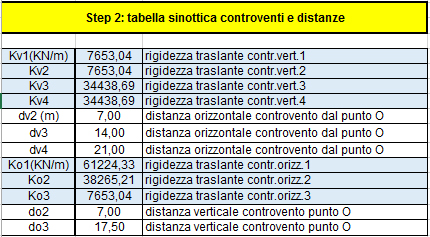
STEP 2

Nella seconda tabella sono riportate le rigidezza di ogni telaio, e la distanza di ciascuno di

essi dall'origine.

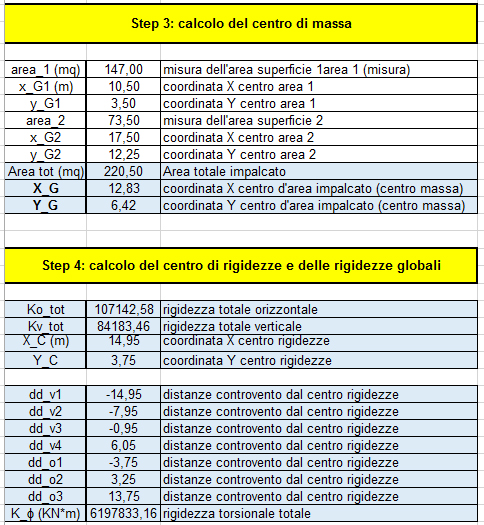
STEP 3 e STEP 4

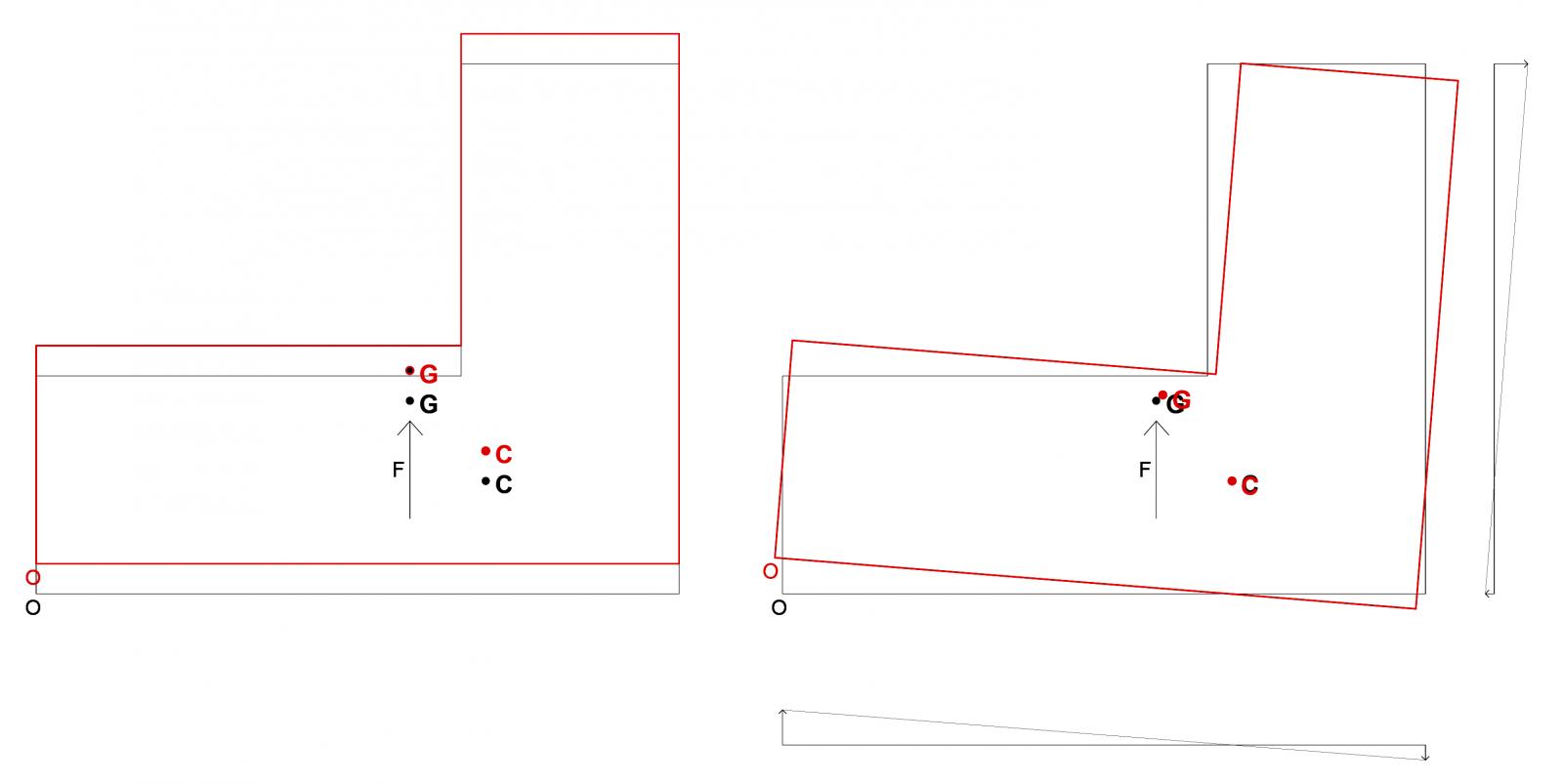
La terza e quarta tabella servono a trovare il centro di massa G e il centro delle rigidezze C.

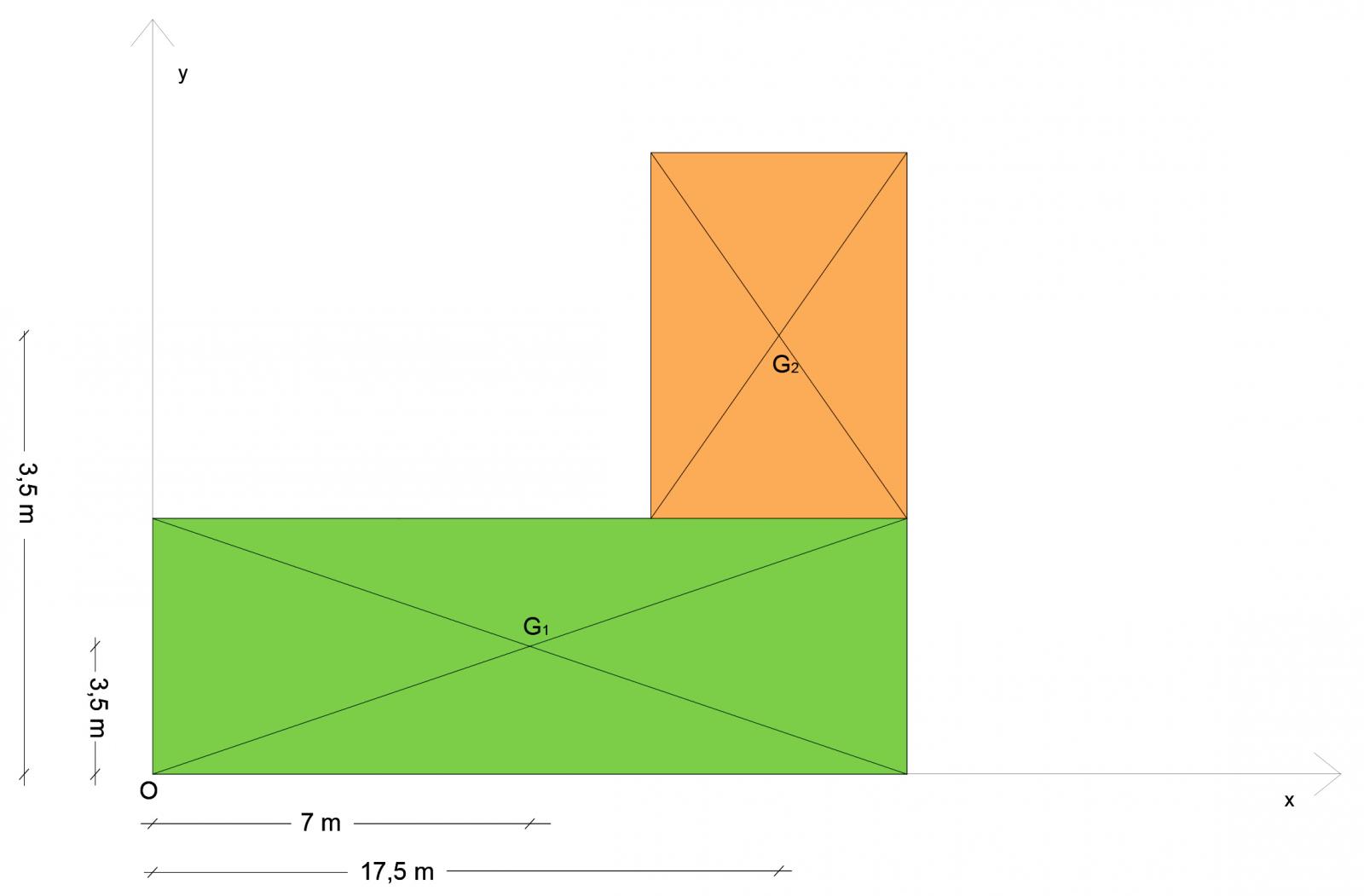
Per calcolare G suddivido l'impalcato in due figure elementari

1) il rettangolo verde, di area pari a 147,00 mq

2) il rettangolo arancione, di area pari a 73,50 mq

Dopo aver individuato il centro di massa dei due rettangoli, trovo G dell'impalcato con la

seguente formula:

x_G = A₁ x_G1 + A₂ x_G2  / A_tot

y_G = A₁ y_G1 + A₂ y_G2  / A_tot

Il centro di massa G dell'impalcato ha coordinate (12,83; 6,42).

Sostituendo nella formula del centro di massa la rigidezza dei telai al posto dell'area e la loro

distanza da O al posto di x_G1, x_G2, y_G1 e y_G2 è possibile trovare il centro delle rigidezze C

dell'impalcato.

Il centro delle rigidezze C dell'impalcato ha coordinate (14,95; 3,75).

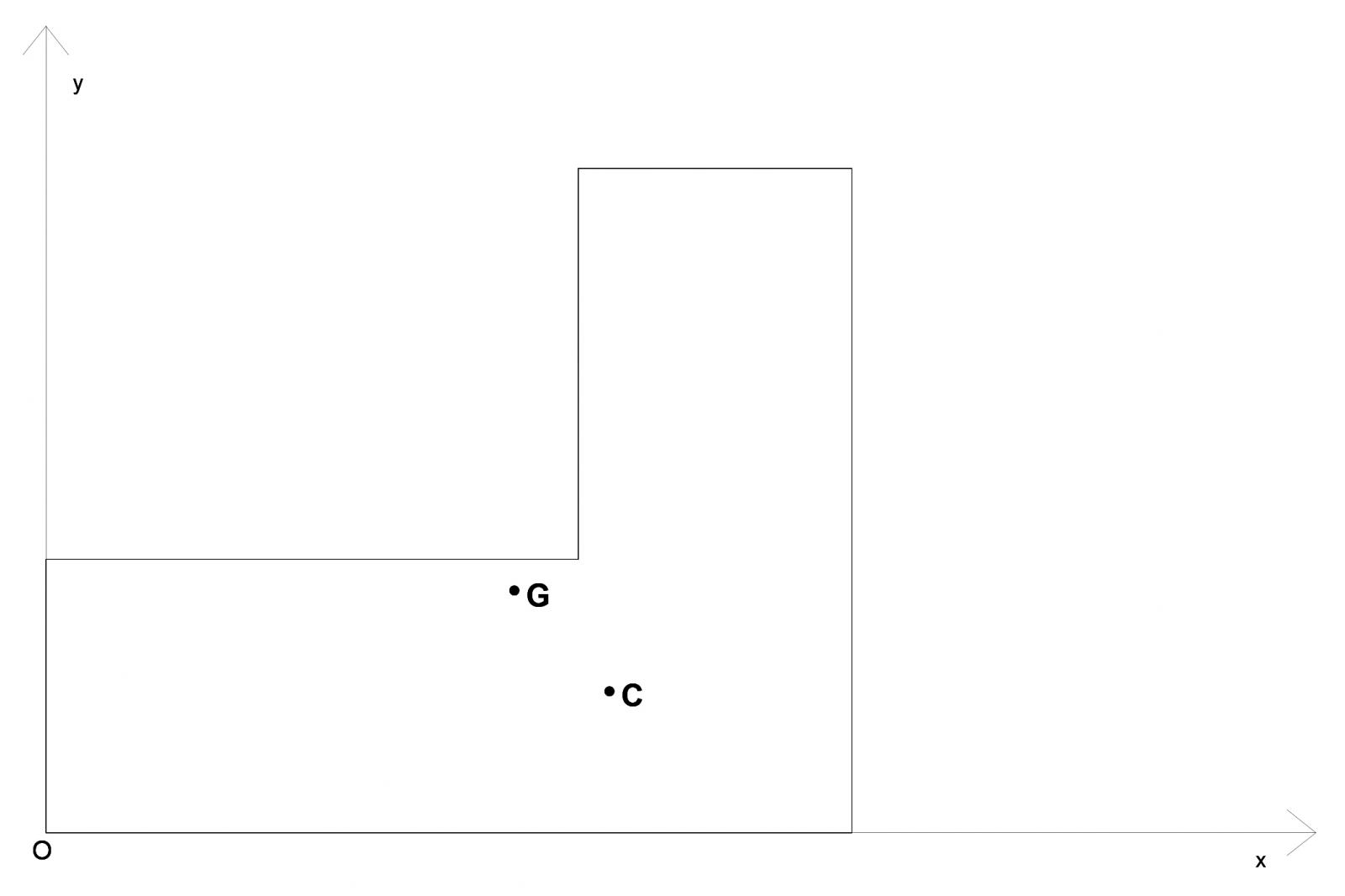
Siccome la forza sismica F, sia in direzione x che in direzione y, viene applicata nel centro di

massa, se G e C coincidessero l'impalcato sarebbe soggetto solo a traslazione verticale e

orizzontale. In questo caso però G e C non coincidono e la loro distanza crea un braccio che

genera un Momento. Quindi la forza sismica, oltre alla traslazione, provocherà anche una

rotazione.

STEP 5

Nella quinta tabella attraverso l'analisi dei carichi sismici siamo in grado di ricavare la forza

sismica complessiva che agisce sul centro di massa. Ho ripreso i valori di q_s, q_p e q_a trovati

nella prima esercitazione, mentre il valore del coefficiente di contemporaneità ψ = 0,3 è dato

dalla destinazione d'uso ( residenziale) dell'edificio. Il valore del coefficiente di intensità

sismica c è invece dato dall'area geografica dell'edificio e in questo caso c = 0,10. 

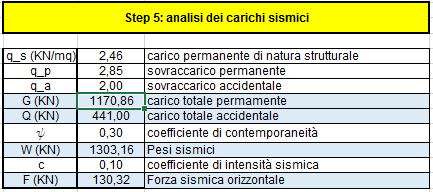
La forza sismica F = 130, 32 KN e deve essere applicata sia in direzione x che in

direzione y. 

STEP 6 e STEP 7

Le ultime due tabelle servono a capire la ripartizione della forza sismica sui vari telai e quali

effetti essa produca sull'impalcato. Nella tabella 6 si analizza la traslazione e la rotazione

dovute a Fx, mentre nella tabella 7 quelle dovute a Fy.

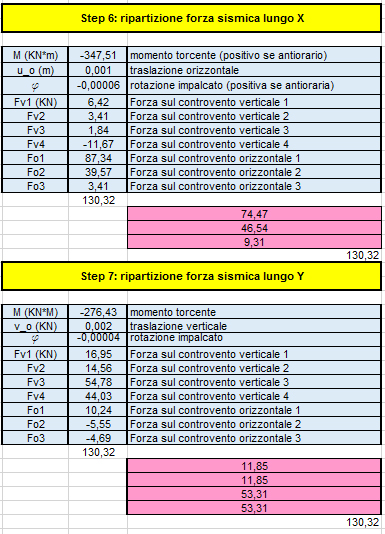
Schematicamente possiamo dire che gli effetti dovuti a Fx sono:

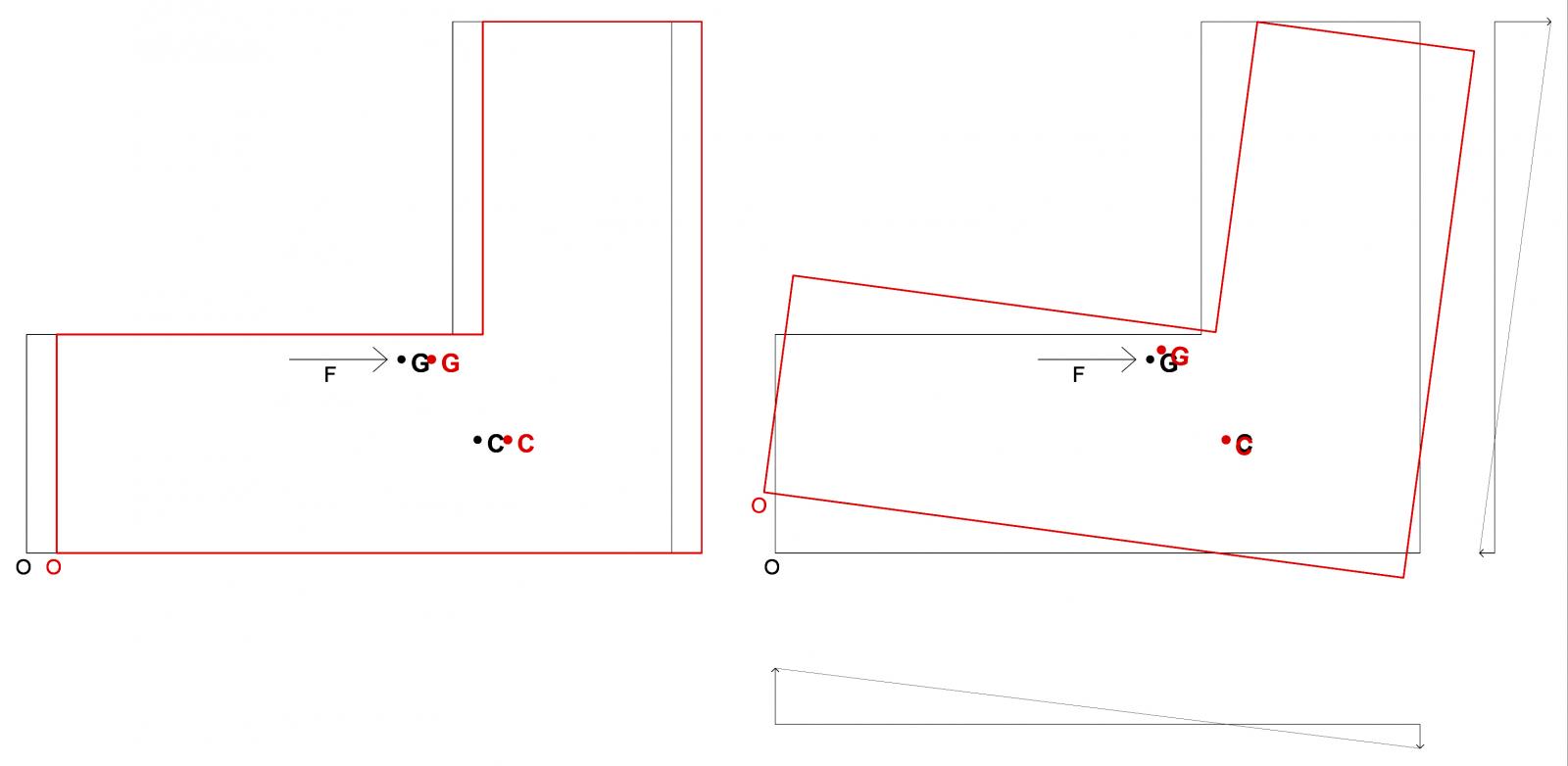
Mentre quelli provocati da Fy sono: