Es_3 Deformazione di una mensola
Per questa esercitazione è stato richiesto di studiare il comportamento di una mensola di un telaio a nostra scelta nelle tre tecnologie:legno, cls armato e acciaio. Il telaio da me scelto è un evoluzione di quello utilizzato per la prima esercitazione. Gli aggetti della mensola non sono fantasiosi, sono di 2,5 m. (f.1)
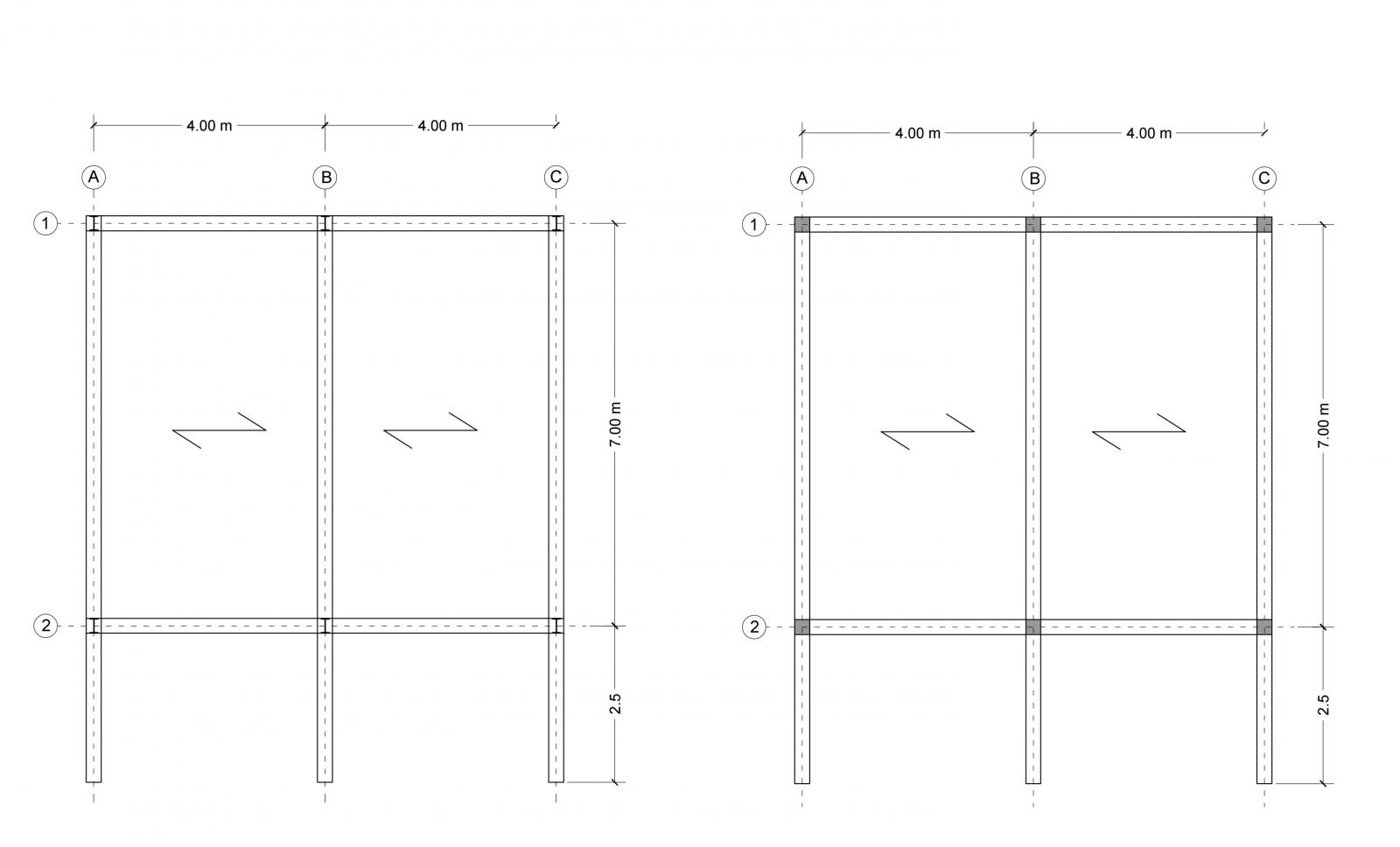 f.1
f.1
L'area d'influenza della trave A = I x L = 4 m x 2,5 m = 10 m2 è evidenziata in azzurro (f.2) La trave più sollecitata è quella centrale.
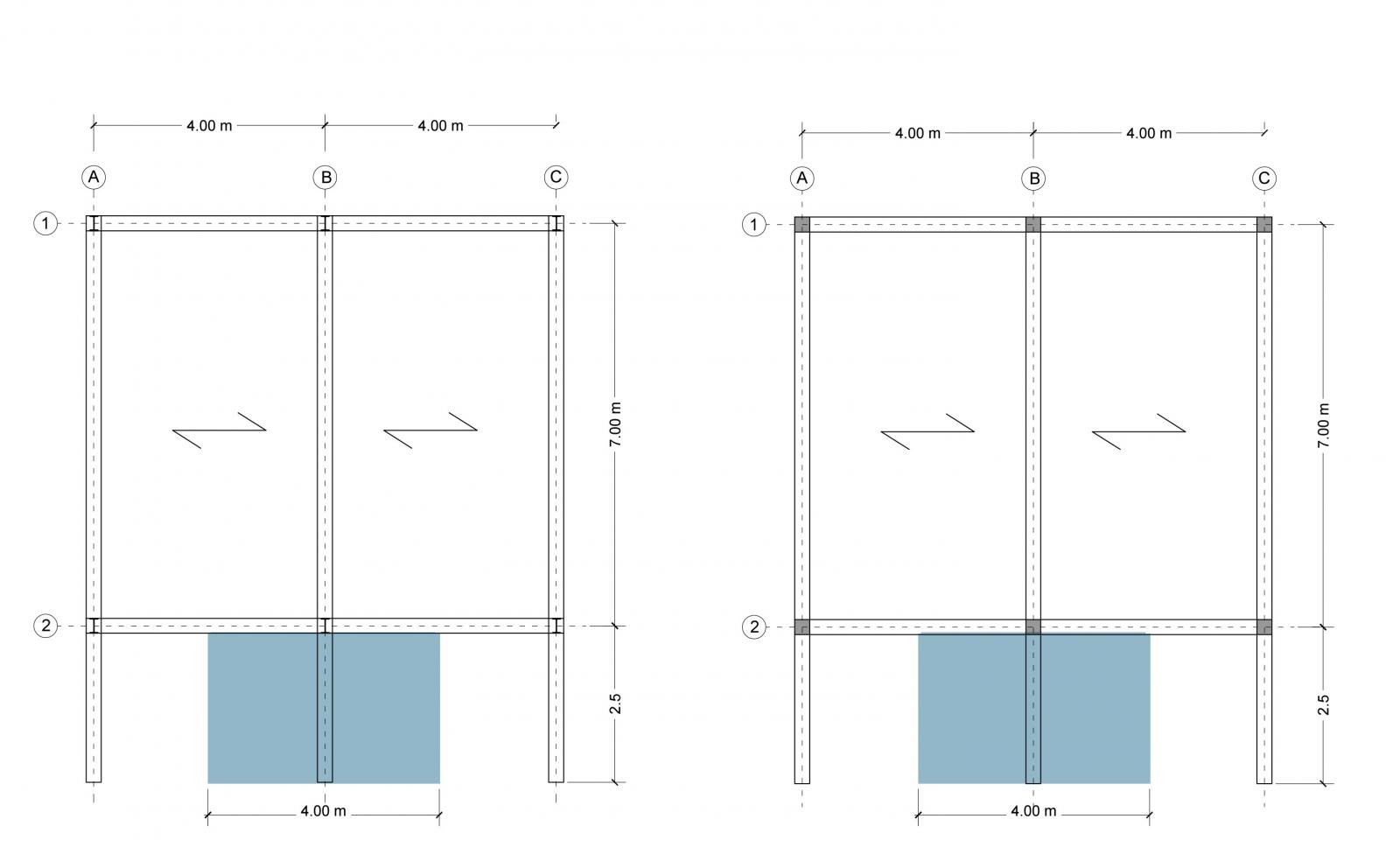 f.2
f.2
I pacchetti di solaio utilizzati, sono gli stessi della prima esercitazione.
Legno
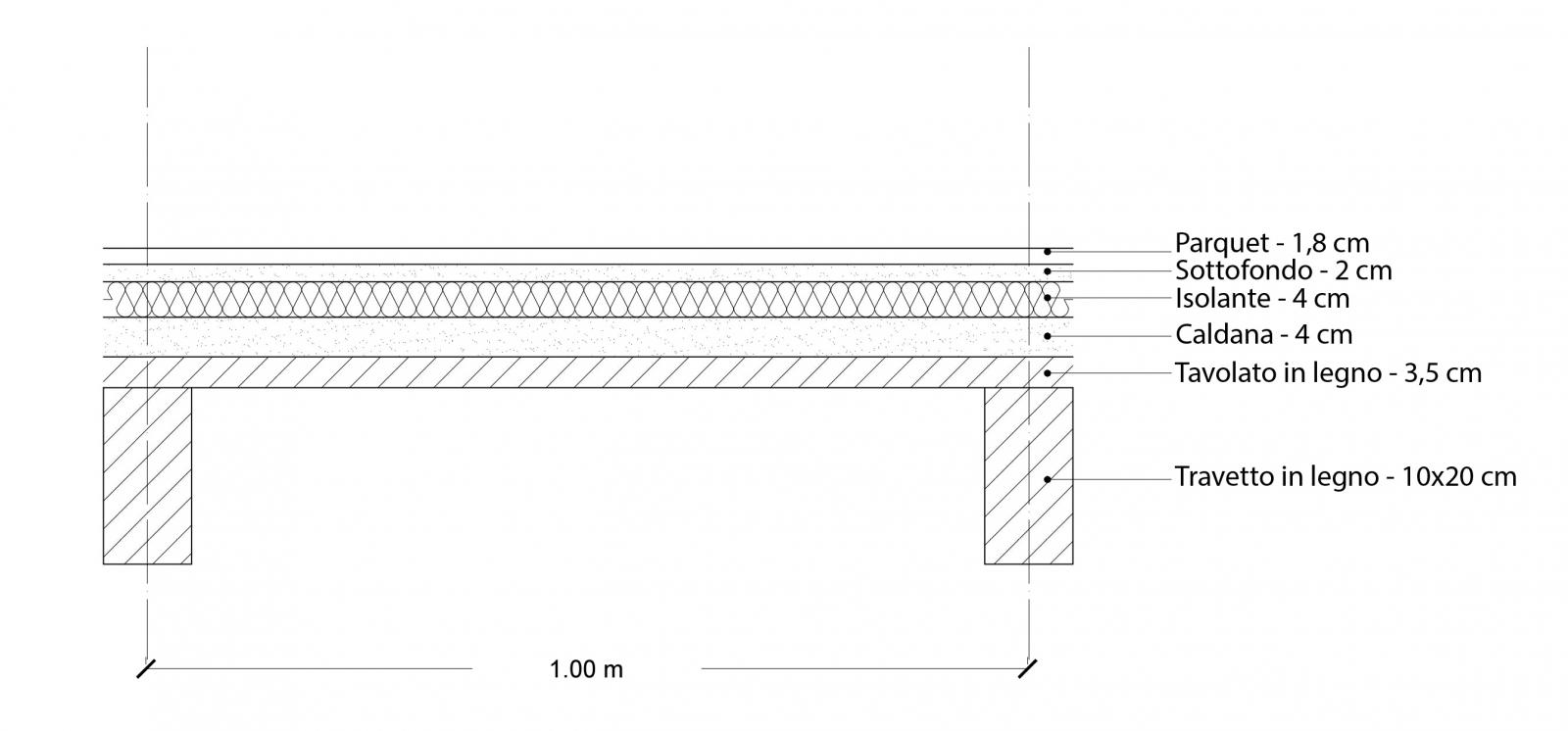
Calcolo dei carichi strutturali qs (escluso peso proprio della trave)
qs = 0,1 kN/mq + 0,21 kN/mq = 0,31 kN/mq
Calcolo dei carichi portati qp
qp = (0,7 + 0,012 + 0,4 + 0,13 + 0,5 + 1) = 2,742 kN/mq
Calcolo dei carichi accidentali qa
qa = 2 kN/mq
Questa volta ho a disposizione un nuovo foglio excel, questo foglio mi permette di controllare che la mia trave non si deformi troppo. Il momento inserito in tabella però non è più qL2/8 ma qL2/2 in quanto siamo in presenza di una mensola.
Come per la precedente esercitazione, inserisco i dati da me conosciuti dopo aver scelto il tipo di legno che voglio utlizzare, e ipotizzo una base 25 cm, e partendo da un Hmin ipotizzo un altezza di 50 cm; ottenendo così una sezione rettangolare 25x50cm. Devo però per prima cosa capire se la mia sezione è stata dimensionata nel modo giusto una volta preso in considerazione il peso proprio della trave.
Pt = [(0,25 m x 0,50 m x 1 m)/mq] x (5 kN/mq) = (0,125 mc/mq) x (5 kN/mq) = 0,625
qu= (qs x 1,3) + (qp x 1,5) + (qa x 1,5) + (Pt x 1,3)
Dopo aver insierito anche questo dato controllo che la deformazione della mia trave sia accettabile. In questo caso lo è in quanto vmax = 0,38 cm (f.4)
 f.4
f.4
Acciaio
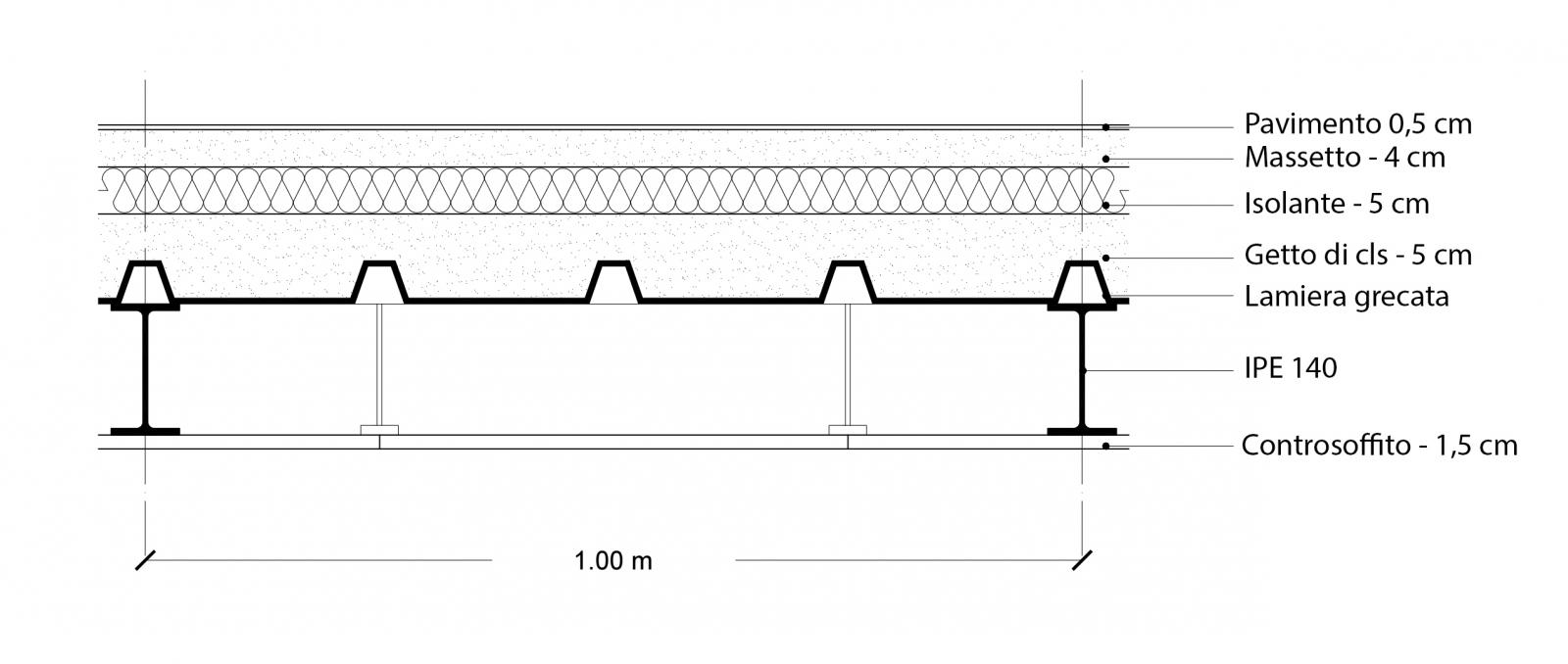
Calcolo dei carichi strutturali qs (escluso peso proprio della trave)
qs = 0,1256 kN/mq + 0,0589 kN/mq + 1,97 kN/mq = 2,15 kN/mq
Calcolo dei carichi portati qp
qp = 0,17 kN/mq + 0,015 kN/mq + 0,96 kN/mq + 0,035 kN/mq + 1 kN/mq + 0,5 kN/mq = 2,68 kN/mq
Calcolo dei carichi accidentali qa
qa = 2 kN/mq
Procedo come fatto per il legno, inserisco i dati da me conosciuti all'interno della tabella. In questo caso mi dovrò ricavare un Wx min che tramite tabellario mi permetterà di ingegnerizzare la mia sezione scegliendo un IPE con un Wx appena superiore. Come per il legno devo prendere in considerazione il peso proprio della trave.
Il profilato IPE 300 ha un area di 53,81 cmq = 0,005381 mq con un P = 78,5 kN/mc.
Pt= [(0,005381 mq x 1 m)/mq] x (78,5 kN/mc) = (0,005381 mc/mq) x (78,5 kN/mc) = 0,422 kN/mq
Inserisco il peso proprio della trave a qu moltiplicato per 1,3
qu= (qs x 1,3) + (qp x 1,5) + (qa x 1,5) + (Pt x 1,3)
Dopo aver insierito anche questo dato controllo che la deformazione della mia trave sia accettabile. In questo caso lo è in quanto vmax = 0,66 cm (f.6)
 f.6 (la prima riga rappresenta la mia trave)
f.6 (la prima riga rappresenta la mia trave)
Cemento Armato
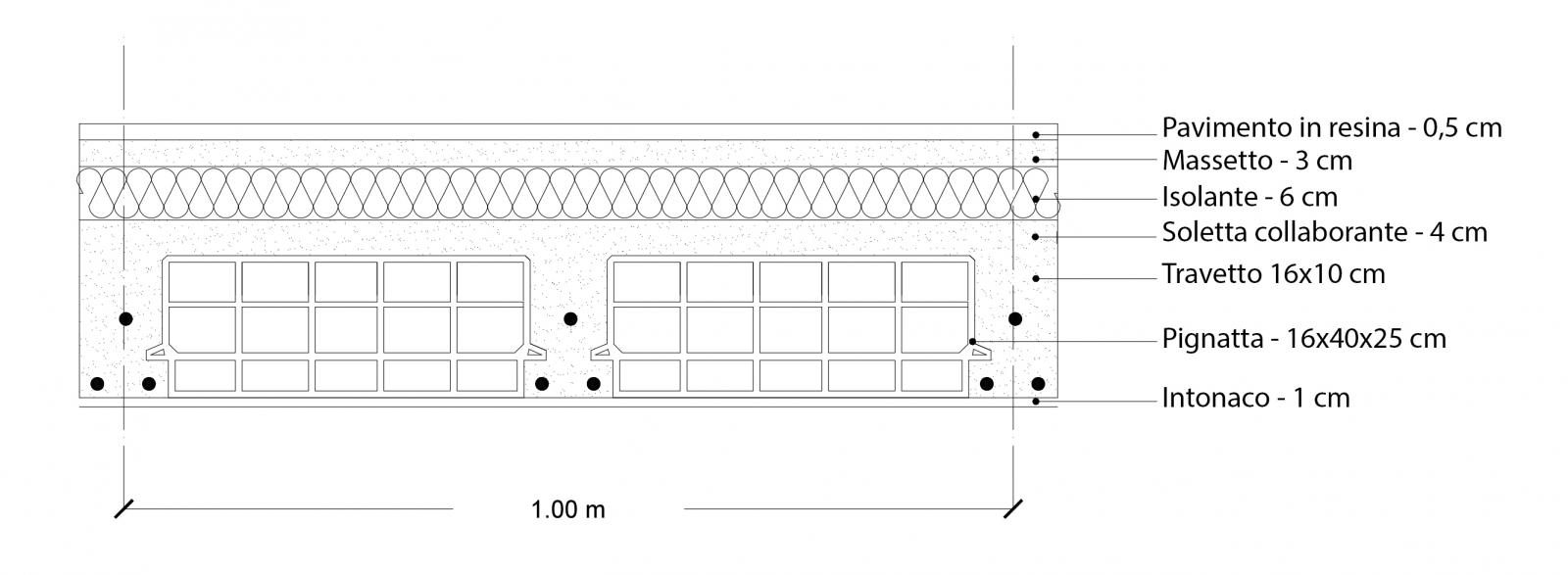
Calcolo dei carichi strutturale qs (escluso peso proprio della trave)
qs= 0,768 kN/mq + 0,738 kN/mq + 0,96 kN/mq = 2,46 kN/mq
Calcolo dei carichi portati qp
qp= 0,13 kN/mq + 0,57 kN + 0,018 kN/mq + 0,18 kN/mq + 0,5 kN/mq + 1 kN/mq = 2,39 kN/mq
Calcolo dei carichi accidentali qa (da norma):
qa = 2 kN/mq
Come per legno e acciaio, scelgo il tipo di cemento e di ferro per l'armatura e inserisco i dati in tabella. Ipotizzo una sezione rettangolare di 30x50 cm. Non devo calcolare il peso proprio in questo caso in quanto viene gia preso in considerazione e esemplificato nella tabella.
Controllo che la deformazione della mia trave sia accettabile. In questo caso lo è in quanto vmax = 0,20 cm (f.8)

