blog di Matteo Molinari

La quinta esercitazione consiste nel calcolare attraverso il metodo delle rigidezza come una forza orizzontale (vento o sismica) si ripartisca sui telai che compongono la struttura.

Per questa esercitazione ho preso in considerazione una struttura semplificata di un piano tipo dell’edificio in fase di progettazione nel Laboratorio di Progettazione Architettonica del prof. Desideri.

La struttura è in calcestruzzo armato.

Il primo passo consiste nel disegnare la pianta di carpenteria e individuare i telai verticali e orizzontali. In questo caso si hanno 11 telai, 6 verticali e 5 orizzontali.

To1 = p. 1, p. 2, p. 3, p. 4

To2 = p. 5, p. 6, p. 7, p. 8

To3 = p. 9, p. 10

To4 = p. 11, p. 12, p. 13, p. 14

To5 = p. 15, p.16, p. 17, p, 18

Tv1 = p. 1, p. 5, p. 9, p. 11, p. 15

Tv2 = p. 2, p. 6, p. 10, p. 12, p. 16

Tv3 = p. 3, p.7

Tv4 = p. 4, p. 8

Tv5 = p. 13, p. 17

Tv6 = p.14, p. 18

La sezione dei pilastri presi in considerazione è di 30x40 cm

Devo calcolare il momento d’inerzia rispetto all’asse x e all’asse y

Ix = bh³/12 = 40x30³/12 = 90.000 cm⁴

Iy = bh³/12 = 30x40³/12 = 160.000 cm⁴

Una volta calcolato inserisco il momento d'inerzia nella tabella excel. Ho dovuto modificare tutto il foglio excel e le relative formule per poter prendere in considerazione più di 7 telai.

Una volta fatto questo, posso rappresentare in pianta i controventi come delle molle.

 

A questo punto bisogna calcolare il centro di massa della struttura. Per poter fare ciò devo dividere la struttura in figure geometriche elementari. Questo rende possibile trovare il centro d'area, che coincide con il centro di massa in questo caso,  di ogni figura per poi trovare quello comune. Divido la mia struttura in 3 rettangoli.

Rettangolo 1: Area 60 mq

Rettangolo 2: Area 33 mq

Rettangolo 3: Area 45 mq

Per trovare il centro dell'intero impalcato devo applicare due semplici formule, una per le coordinate x e una per le coordinate  y

X_g= A₁*X_g1 + A₂*X_g2 + A₃*X_g3 / A_{to  Le formule sono delle sommatorie, se avessi avuto quattro aree avrei dovuto utilizzarne 4.}

Y_g= A₁*Y_g1 + A₂*Y_g2 + A₃*Y_g3 / A_tot

Rappresento il centro d'area nel mio impalcato:

Nel disegno si può vedere come ho suddiviso la struttura nei 3 rettangoli e dove è posizionato il centro d'area.

Adesso devo trovare il centro delle rigidezze. CI sono due possibilità, la prima che coincida con il centro d'area, e la seconda che sia spostato. La prima opzione è la più favorevole, ma in questo caso, ancora prima di fare i calcoli ci si accorge che i due punti non si potranno mai trovare nello stesso punto. Quindi la struttura oltre a subire una traslazione subisce anche una rotazione. Per fare in modo che la rotazione sia piccola devo fare in modo che il braccio sia molto ridotto. Da cosa è dato il braccio? il braccio è la distanza tra il cento delle rigidezze e il centro d'area dell'impalcato.

Mi calcolo le coordinate del centro delle rigidezze e poi lo schematizzo nella pianta dell'impalcato.

Adesso devo calcolarmi G Q W per poter fare l'analisi dei carichi sismici

G = (q_s + q_p) x A_tot 

Q = q_a x A_tot ​

 

 W = G + (Q x  ψ)

Il coeff. c invece è un valore da inserire e corrisponde alla pericolosità sismica dell'area, serve a ridurre l'accelerazione del di gravità. per Roma c = 0,10

L'ultima fase è vedere come la forza sismica agisce sui controventi orizzontali e verticali:

In questa quarta esercitazione è richiesto di dimensionare a compressione un pilastro nelle tre tecnologie: legno, acciaio cemento.

Per questa consegna ho deciso di utilizzare la stessa carpenteria utilizzata nella prima esercitazione, aumentando semplicemente di una campata la struttura. Questo mi permette di utilizzare la stessa trave principale che avevo dimensionato a flessione e gli stessi pacchetti di solaio. 

La struttura ipotizzo sia alta tre piani, con un altezza netta di 2,70 m per piano.

f.1

f.2

La prima cosa da fare è capire qual’è il pilastro maggiormente sollecitato, in questo caso è il B2 in quanto A = L1 x L2 = 4 m x 7 m = 28 mq. Possiamo vedere l'area d'influenza graficizzata nella f.1 e f.2

 

Legno

In quanto devo calcolare lo sforzo normale che grava sul mio pilastro, il riutilizzare la carpenteria dimensionata nella prima esercitazione è stato fondamentale per ridurre di molto i passaggi. f.3

f.3

Il primo passaggio è stato calcolare attraverso la tabella l’area d’influenza della trave, per poi andare a inserire: il peso proprio della trave principale e secondaria, i carichi che gravano sul pilastro e quanti piani ha il mio edificio. Inserire il numero di piani è fondamentale. Questo ci ha permesso ci calcolare lo sforzo Normale che grava sul pilastro con la formula:

N = ( Q_trave x Q_solaio ) x n_piani 

Il prossimo passaggio consiste nell’inserire le caratteristiche di resistenza del materiale. Per il pilastro ho deciso di usare le stesse utilizzate per la trave, quindi un F_ck = 24 MPa k_mod = 0,80 e Y_m=1,45.

Una volta Inserite questi valori nel foglio excel attraverso delle formula pre impostate mi calcola l’area minima che il mio pilastro deve avere. f.4

f.4

L’ultima parte della tabella mi permette di calcolarmi la sezione del pilastro e poi verificare che A_d<A_min

Per poter arrivare a questo punto però devo definire il modulo elastico del materiale, il Beta del pilastro e la sua altezza. Fatto questo ipotizzo una base, e la tabella mi dice rispetto alla base da me scelta qual’è l’altezza minima della sezione del pilastro. f.5

f.5

Nel mio caso con una forza Normale di 664 kN, un A_min = 501,3 ho scelto una base di 15 cm con un H_min = 33,42. Questo mi ha permesso di scegliere una sezione di 15 cm x 35 cm in quanto l’altezza di 33 cm era troppo specifica e non rispettava i canoni di produzione industriali dei profilati pre-impostati.

L’ultima verifica da fare è vedere se l’ A_design>A_min in questo caso 525 cmq >501,3 cmq

VERIFICATO 

 

CLS

Come nel legno ho riutilizzato il pacchetto solaio calcolato nella prima esercitazione. f.6

f.6

Nel dimensionare il pilastro avevo pensato di utilizzare lo stesso fck utilizzato per il dimensionamento a flessione della trave cioè 60MPa. Mi sono accorto però col procedere dei i calcoli che era esagerato in quanto la sezione veniva troppo piccola e il pilastro troppo snello. Per questo ho deciso di utilizzare un f_ck = 40 MPa.

Per il dimensionamento a compressione del pilastro bisogna effettuare due verifiche:

1. A_design>A_min
2. σ_max<f_cd

Facendo un ragionamento di dimensionamento solo a compressione il materiale da tenere in conto è il cemento.

Come per il legno inserisco in tabella tutti i dati relativi all’area d’influenza e ai carichi in modo da ottenere la forza normale agente sul pilastro. Una volta ottenuta la forza normale posso continuare inserendo il valore di f_ck, E, Beta e l’altezza del pilastro. Fatto questo ottengo dei valori di base e altezza minimi.

f.7

f.8

Ho notato che dimensionando il pilastro aumentando leggermente le dimensioni rispetto a quelle minime per esempio 20x20 ottengo il punto 1 verificato ma non il punto 2. Per far si che il σ_max<f_cd devo utilizzare una sezione di 40 x 40 cm infatti ottengo: 

1. 1600 cmq > 415 cmq

2. 20,87<22,7

VERIFICATO

 

Acciaio 

Come per il legno e cls riutilizzo il pacchetto solaio della prima esercitazione e inserisco i dati nella tabella.

f.9

Come per il cemento ho due verifiche da fare:

1. A_design>A_min
2. λ<λ_max

 

Come per il dimensionamento della trave a flessione ho scelto di utilizzare un acciaio con un coefficiente di resistenza f_yk = 275 MPA

Dopo aver inserito tutti i dati conosciuti ottengo un valore di Amin e attraverso una tabella cerco il suo profilo industriale. Devo utilizzare un HEA in quanto un IPE non è adatta ad essere utilizzata come pilastro in quanto è specificamente disegnata per resistere a sforzi a flessione.

La mia area minima è di 32,3 cm quindi scelgo la prima area più grande industrializzata che corrisponde a 38,8 cm, un HEA 160.

f.10

Ottengo:

1.  38,8 cmq > 32,3 cmq

2. 67,84 < 88,96

VERIFICATO

 

Considerazioni

Importante notare che il dimensionamento del pilastro è stato fatto senza considerare la presenza dei pilastri sui piani superiori. 

Un ragionamento da fare sarebbe aggiungere al carico totali anche il peso di tutti i pilastri presenti in quella parte di solaio che grava sul pilastro che io voglio dimensionare.

Passaggio 1 : dimensionamento del pilastro preliminare

Passaggio 2 : ridimensiono il pilastro riutilizzando come sezione di base quella calcolata nel passaggio 1 ma aggiungendo al Qtot anche il peso dei pilastri

Passaggio 3 : Verifico che la sezione scelta nel Passaggio 1 sia verificata nel Passaggio 2  se no devo aumentare la sezione.

Un altro modo potrebbe essere cominciare a dimensionare il pilastro dall'ultimo piano, in modo da sapere sempre la sezione del pilastro al piano superiore. Ovvimanete più si va in alto più la sezione del pilastro dovrebbe diminuire in quanto vi sono meno forze verticali che agiscono su esso.

In quanto il legno è un materiale leggero in alcuni casi è possibile non effettuare quest’ulteriore verifica.

Per questa esercitazione è stato richiesto di studiare il comportamento di una mensola di un telaio a nostra scelta nelle tre tecnologie:legno, cls armato e acciaio. Il telaio da me scelto è un evoluzione di quello utilizzato per la prima esercitazione. Gli aggetti della mensola non sono fantasiosi, sono di 2,5 m. (f.1)

f.1

L'area d'influenza della trave A = I x L = 4 m x 2,5 m = 10 m² è evidenziata in azzurro (f.2) La trave più sollecitata è quella centrale.

f.2

I pacchetti di solaio utilizzati, sono gli stessi della prima esercitazione.

Legno

Calcolo dei carichi strutturali   qs (escluso peso proprio della trave)

qs = 0,1 kN/mq + 0,21 kN/mq = 0,31 kN/mq

Calcolo dei carichi portati     qp

qp = (0,7 + 0,012 + 0,4 + 0,13 + 0,5 + 1) = 2,742 kN/mq

Calcolo dei carichi accidentali     qa

qa = 2 kN/mq

Questa volta ho a disposizione un nuovo foglio excel, questo foglio mi permette di controllare che la mia trave non si deformi troppo. Il momento inserito in tabella però non è più qL²/8 ma qL²/2 in quanto siamo in presenza di una mensola.

Come per la precedente esercitazione, inserisco i dati da me conosciuti dopo aver scelto il tipo di legno che voglio utlizzare, e ipotizzo una base 25 cm, e partendo da un Hmin ipotizzo un altezza di 50 cm; ottenendo così una sezione rettangolare 25x50cm. Devo però per prima cosa capire se la mia sezione è stata dimensionata nel modo giusto una volta preso in considerazione il peso proprio della trave.

Pt = [(0,25 m x 0,50 m x 1 m)/mq] x (5 kN/mq) = (0,125 mc/mq) x (5 kN/mq) = 0,625

qu= (qs x 1,3) + (qp x 1,5) + (qa x 1,5) + (Pt x 1,3)

Dopo aver insierito anche questo dato controllo che la deformazione della mia trave sia accettabile. In questo caso lo è in quanto vmax = 0,38 cm (f.4)

f.4

Acciaio

Calcolo dei carichi strutturali qs (escluso peso proprio della trave)

qs = 0,1256 kN/mq + 0,0589 kN/mq + 1,97 kN/mq = 2,15 kN/mq

Calcolo dei carichi portati qp

qp = 0,17 kN/mq + 0,015 kN/mq + 0,96 kN/mq + 0,035 kN/mq + 1 kN/mq + 0,5 kN/mq = 2,68 kN/mq

Calcolo dei carichi accidentali     qa

qa = 2 kN/mq

Procedo come fatto per il legno, inserisco i dati da me conosciuti all'interno della tabella. In questo caso mi dovrò ricavare un Wx min che tramite tabellario mi permetterà di ingegnerizzare la mia sezione scegliendo un IPE con un Wx appena superiore. Come per il legno devo prendere in considerazione il peso proprio della trave.

Il profilato IPE 300 ha un area di 53,81 cmq = 0,005381 mq con un P = 78,5 kN/mc.

Pt= [(0,005381 mq x 1 m)/mq] x (78,5 kN/mc) = (0,005381 mc/mq) x (78,5 kN/mc) = 0,422 kN/mq

Inserisco il peso proprio della trave a qu moltiplicato per 1,3

qu= (qs x 1,3) + (qp x 1,5) + (qa x 1,5) + (Pt x 1,3)

La seconda esercitazione consiste nel dimensionare una travatura reticolare a nostra scelta. Nel mio caso ho optato per una travatura reticolare composta da corpi cubici di luce 2 m, con aste inclinate ti 2,82 m. Il corpo consiste di 3x5 moduli, quindi 6x10m. (fig.1)

f.1

Per disegnare la trave reticolare ho utilizzato SAP2000. Come si può vedere nella f. 1 ho vincolato la trave alle 4 estremità con un vincolo a cerniera, ASSIGN, JOINTS, RESTRAIN. Per questa esercitazione ho deciso di usare delle aste tubolari, quindi è stato necessario assegnare a ciascuna asta la sezione cilindrica sul programma tramite il comando ASSIGN, FRAME, FRAME SECTION. (f.2) é stato necessario rimuovere anche i momenti dalle aste. In quanto trave reticolare e non soggetta a Momento Flettente ma solamente a sforzi di compressione e trazione.

f.2

Ai nodi superiori, ho assegnato una forza concentrata F=150 kN (f.3) Il valore immesso è negativo in quanto deve essere rivolta verso il basso.

f.3

Una volta assegnati i carichi, aver controllato che non vi sono doppie aste una sopra l'altra, aver controllato le giunture e il moltiplicatore di peso della trave sia 0 posso far partire l'analisi.

Appena finita, l'analisi, mi mostra la travatura deformata (f.4) ma posso anche impostare una vista che mi permette di vedere il corpo prima della deformazione con i diagrammi di sforzo normale (f.5). Dimensionare una trave guardando gli sforzi solo dal 3d sarebbe troppo complicato, quindi tramite il comando SHOW TABLES posso esportare un file excel, con tutte le aste e i loro rispettivi sforzi normali. Le aste sono numerate, in modo da poter controllare quali siano quelle inclinate e quali non.

f.4

f.5

Una volta esportato il file excel, la prima cosa è rimuovere tutti i doppioni. Infatti SAP fa un analisi ogni 0,5 m, questo fa si che nella mia tabella io abbia 5 valori per ogni asta (0-0,5-1-1,5-2). Una volta eliminati i doppioni (tramite il comando elimina duplicati) posso riordinare le mie aste per aste soggette a trazione e compressione.

Il dimensionamento per un asta a trazione e compressione è diverso, per questo devo utilizzare due fogli excel differenti. Comincio a spiegare quello a trazione. Io so che nel progetto di un asta tesa:

                                                                                   A=N/f_yd

In quanto N è un valore conosciuto, risultato dalla mia analisi in SAP, f_yd è dato dal rapporto f_yk/ γ_m nel quale fyk  dipende dal tipo di acciaio scelto (nel mio caso S235) posso ricavarmi l'aria minima che la mia asta deve avere. Una volta ricavata l'area minima basta prendere un semplice tabellario e prendere l'asta con l'area direttamente superiore. In questo caso non è importante differenziare tra aste inclinate e aste non, in quanto il dimensionamento non prende in considerazione la luce dell'asta. (f.6-f.7-f.8)

f.6

f.7

f.8

Per le aste soggette a sforzo di compressioe il discorso è diverso. In quanto sono soggette all'instabilità euleriana la luce gioca un ruolo fondamentale nel progettare il tipo di asta che si vuole utilizzare. Quindi come ho fatto nelle aste tese, devo ricavarmi un Amin, l'area a questo punto non è più il solo fattore che influenza la trava ma anche il momento d'inerzia e il raggio d'inerzia. Ingegnerizzando la mia asta devo infatti prestare attenzione che i valori I, ro e Lambda del profilato da me scelto in base all'area non siano inferiori a I_min , ro_min e lambda_min(f.9) metto un esempio solo delle prime 39 aste

f.9

La E presenta solo un errore di visualizzazione, ho controllato che il valore inserito sia effettivamente ll modulo elastico dell'acciaio.

La prima esercitazione consiste nel dimensionare a flessione una trave in: legno, cemento e acciaio di un telaio a nostra scelta.

Il telaio preso in considerazione (f.1 per legno e cemento, f.2 per acciaio) ha due campate da 4 m con una luce di 7 m.

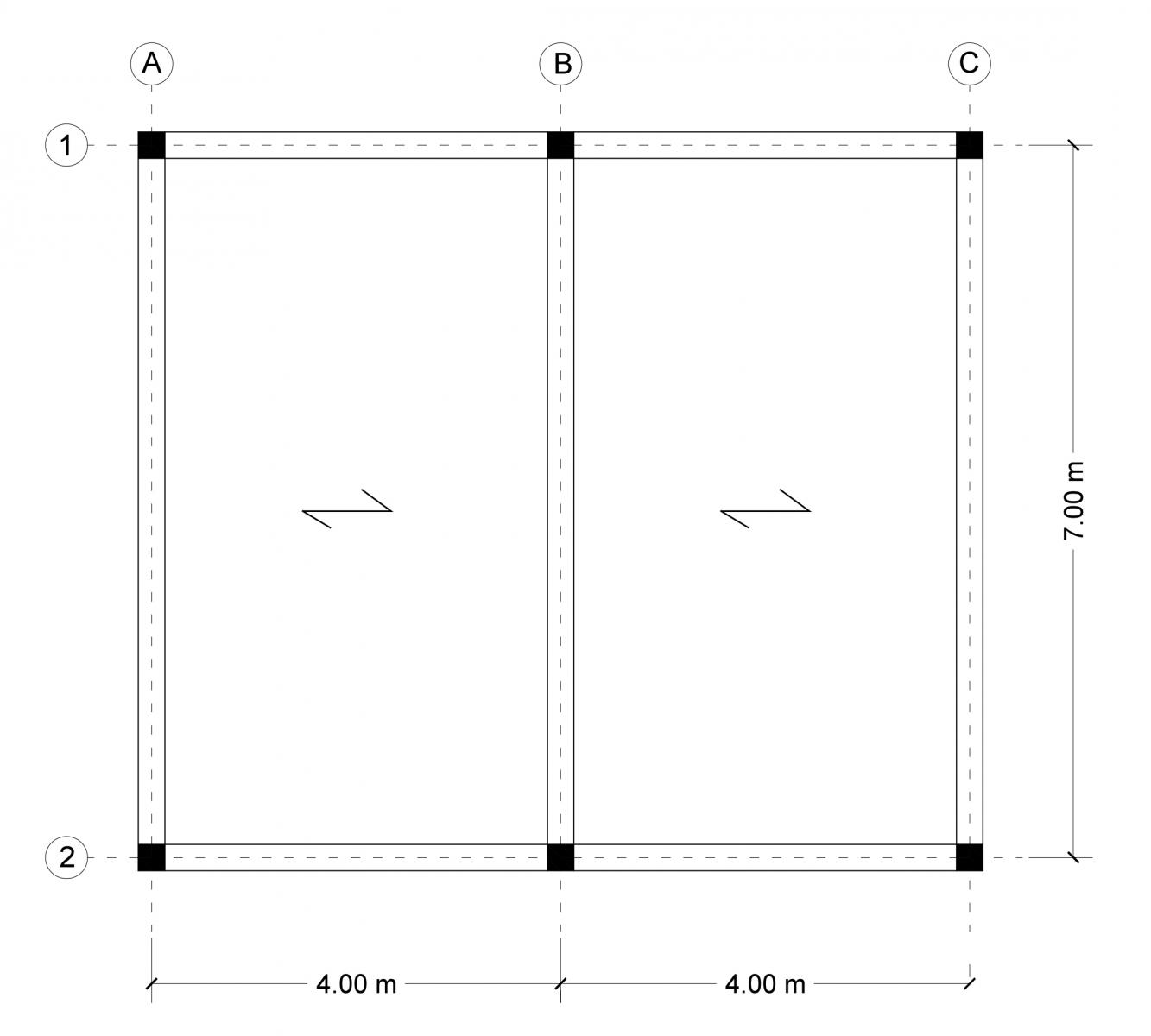f.1f.2

La trave più sollecitata è la trave centrale (B) in quanto ha un'area d'influenza maggiore. (f.3)

A=IxL= 4 m x 7 m = 28mq 

Dove "I" è l'interasse della trave e "L" è la luce.

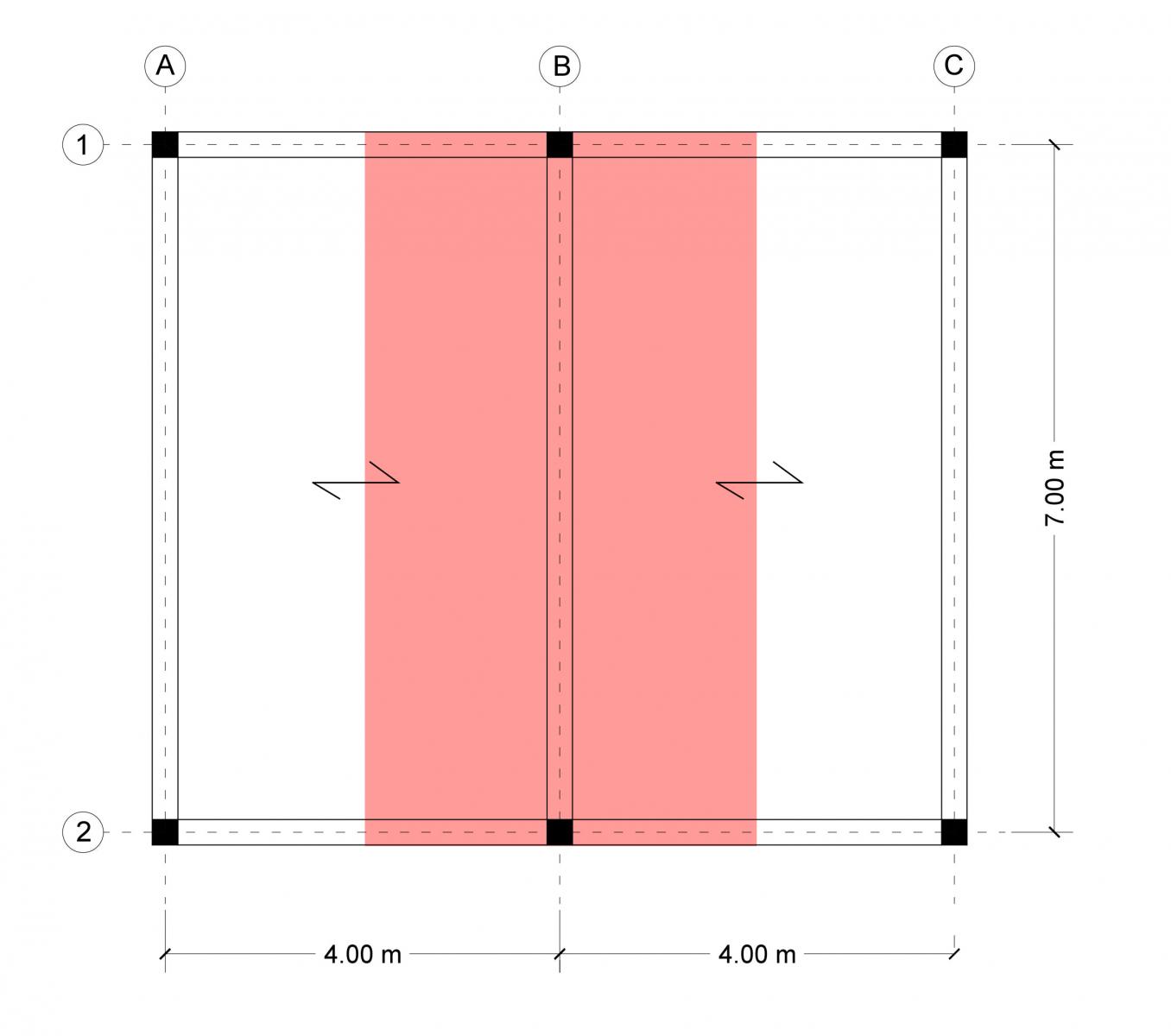                                                          f.3

Dimensionamento di una trave in legno

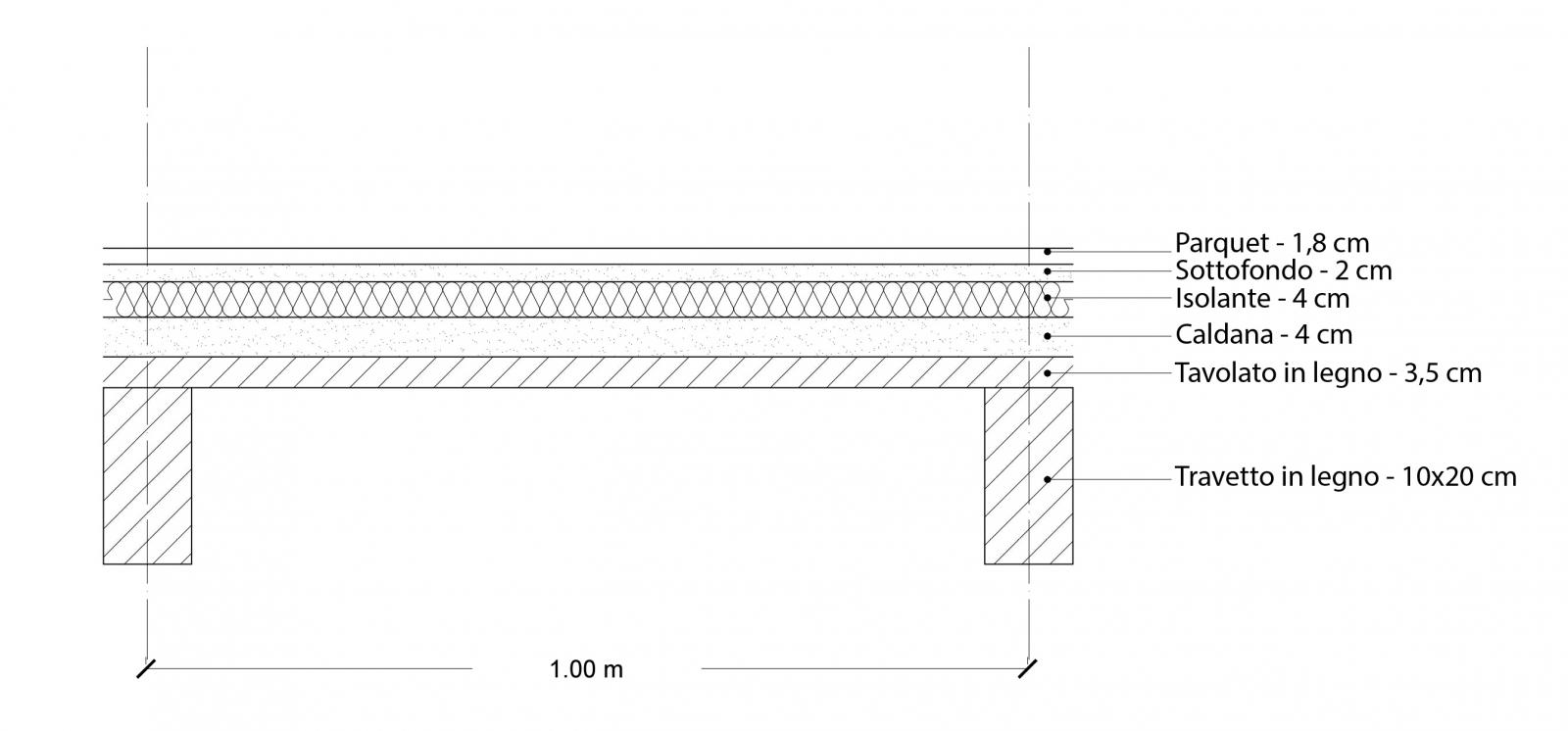                                                         f.4

Elementi che compongono il solaio: (f.4)

Travetti: 20x10 cm                                         P=500 kg/mc

Tavolato: 3,5 cm                                             P=0,21 kN/mq

Caldana: 4,5 cm                                             P=2000 kg/mc

Isolante Termico:  Lana di roccia 4 cm           P=30 kg/mc

Sottofondo: 2 cm                                           P=2000 kg/mc

Pavimento: parquet di rovere 1,8 cm             P=7,2 kN/mc

Calcolo dei carichi strutturali   qs (escluso peso proprio della trave)

Travetti

[(0,2 m x 0,1 m x 1 m)/mq] x (5 kN/mc)= (0,02 mc/mq) x (5 kN/mc) = 0,1 kN/mq

Tavolato

0,21 kN/mq

qs = 0,1 kN/mq + 0,21 kN/mq = 0,31 kN/mq

Calcolo dei carichi portati     qp

Caldana

[(0,035 m x 1 m x 1 m)/mq] x (20 kN/mc) = (0,035 mc/mq) x (20 kN/mc) = 0,7 kN/mq

Isolante Termico

[(0,04 m x 1 m x 1 m)/mq] x (0,3 kN/mc) = (0,04 mc/mq) x (0,3 kN/mc) = 0,012 kN/mq

Sottofondo

[(0,02 m x 1 m x 1 m)/mq] x (20 kN/mc) = (0,02 mc/mq) x (20 kN/mc) = 0,4 kN/mq

Pavimento

[(0,018 m x 1 m x 1 m)/mq] x (7,2 kN/mc) = (0,018 mc/mq) x (7,2 kN/mc) = 0,13 kN/mq

Impianti

0,5 kN/mq

Tramezzi

1 kN/mq

qp = (0,7 + 0,012 + 0,4 + 0,13 + 0,5 + 1) = 2,742 kN/mq

Calcolo dei carichi accidentali     qa

La struttura è per un ambiente ad uso residenziale, quindi da normativa:

qa = 2 kN/mq

Dopo aver calcolato i tre tipi di carico, vado ad inserirli nella tabella excel insieme ai dati dell’interasse e della luce del solaio preso in considerazione. Il momento massimo della trave è dato dalla tabella tramite l'inserimento della formula di M_max di una trave con doppio appoggio ql²/8. Per questo solaio è stato scelto un legno lamellare GL24h con resistenza caratteristica fm,k=24MPa. La resistenza deve essere inserita in tabella. Imposto la base della trave, in questo modo il foglio excel (attraverso delle formule pre-impostate h = l x radq[(3/4) x (q/bxfd)] ) calcola l’altezza minima che la sezione della trave deve avere. (f.5)

f.5

Data un altezza minima di 52 cm, ipotizzo una sezione di 30x55 cm. Il carico strutturale preso in considerazione prima non comprendeva il peso proprio della trave; devo quindi calcolare il peso proprio della trave e inserirlo nel qu moltiplicato per 1,3 e verificare che la sezione scelta sia adatta.

Pt = [(0,30 m x 0,55 m x 1 m)/mq] x (5 kN/mq) = (0,165 mc/mq) x (5 kN/mq) = 0,825

qu= (qs x 1,3) + (qp x 1,5) + (qa x 1,5) + (Pt x 1,3) 

f.6

Dopo aver inserito il carico strutturale comprendente il peso proprio della trave si nota come l’altezza minima non sia più 52 cm ma 53 cm.

L’ipotesi di sezione di trave fatta precedentemente  30x55 cm è quindi verificata. (f.6)

Dimensionamento di una trave in cls armato

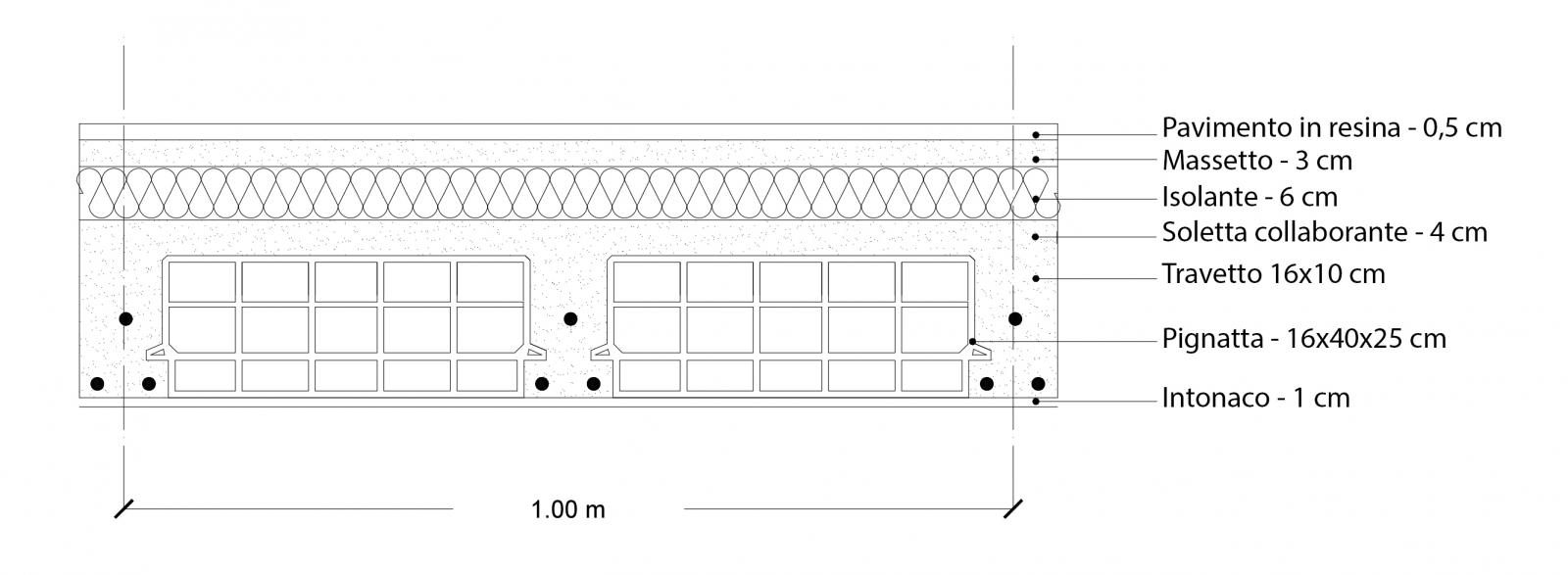                                                     f.7

Elementi che compongono il solaio: (f.7)

Travetti: 10x16 cm                                     P= 24 kN/mc

Pignatte: 16x40x25 cm n=8                       P= 9,1 kg

Soletta Collaborante: 4 cm                          P= 24 kN/mc

Intonaco: 1 cm                                           P= 18 kN/mc

Isolante Termico: lana di roccia 6 cm         P= 30 kg/mc = 0,3 kN/mc

Massetto: 3 cm                                          P= 1900 kg/mc = 19 kN/mc

Pavimento: Parquet di rovere 1,8 cm         P= 7,2 kN/mc

Calcolo dei carichi strutturale qs (escluso peso proprio della trave)

Travetti

2[(0,16 m x 0,10 m x 1 m)/mq] x (24 kN/mc) = (0,032 mc/mq) x (24 kN/mc) = 0,768 kN/mq

Pignatte

sono 8 in 1 mq

8 x 9,1 kg/mq = 73,8 kg/mq = 0,738 kN/mq

Soletta collaborante

[(0,04 m x 1 m x 1 m)/mq] x (24 kN/mc) = (0,04 mc/mq) x (24 kN/mc) = 0,96 kN/mq

qs= 0,768 kN/mq + 0,738 kN/mq + 0,96 kN/mq = 2,46 kN/mq

Calcolo dei carichi portati qp

Pavimento

[(0,018 m x 1 m x 1 m)/mq] x (7,2 kN/mc) = (0,018 mc/mq) x (7,2 kN/mc) = 0,13 kN/mq

Massetto

[(0,03 m x 1 m x1 m)/mq] x (19 kN/mc) = (0,03 mc/mq) x (19 kN/mq) = 0,57 kN/mq

Isolante

[(0,06 m x 1 m x 1 m)/mq] x (0,3 kN/mc) = (0,06 mc/mq) x (0,3 kN/mc) = 0,018 kN/mq

Intonaco

[(0,01 m x 1 m x 1 m)/mq] x (18 kN/mc) = (0,01 mc/mq) x (18 kN/mc) = 0,18 kN/mq

Impianti

0,5 kN/mq

Tramezzi

1 kN/mq

qp= 0,13 kN/mq + 0,57 kN + 0,018 kN/mq + 0,18 kN/mq + 0,5 kN/mq + 1 kN/mq = 2,39 kN/mq

Calcolo dei carichi accidentali     qa (da norma):

La struttura è per un ambiente ad uso residenziale

qa = 2 kN/mq

Inserisco le tre tipologie di carico in tabella exel insieme alla luce e all’interasse come fatto precedentemente per il legno. Scelgo un acciaio per le armature con un coefficiente di resistenza caratteristica per le armature pari a fyk=450 MPa e un calcestruzzo con resistenza a compressione pari a Fck=60 MPa. Imposto una base b pari a 25 cm. Ho scelto questo valore in quanto con una base di 30 l’altezza minima era di 35; la sezione della trave non era adatta in quanto avrebbe presentato un momento d’inerzia non abbastanza grande. Con una base di 25 cm l’altezza utile è di 35 e l’altezza minima di 40,05. (f.8)

f.8

Devo considerare che nel dimensionamento non è stato preso in considerazione il peso proprio della trave quindi è preferibile sovradimensionate la trave con una sezione di 25x45 cm.

Mi calcolo quindi il peso proprio della trave Pt:

Pt = [(0,25 m x 0,45 m x 1 m)/mq] x (25 kN/mc) = (0,1125 mc/mq) x (25 kN/mc) = 2,81 kN/mq

Inserisco il peso proprio della trave a qu moltiplicato per 1,3

qu= (qs x 1,3) + (qp x 1,5) + (qa x 1,5) + (Pt x 1,3) 

f.9

Dopo aver inserito il valore del peso proprio della trave possiamo notare com l’altezza minima sia di 41,65 cm. Quindi era giusta l’ipotesi di una sezione 25x45 cm e la sezione è verificata. (f.9)

DImensionamento di una trave in acciaio

                                            f.10

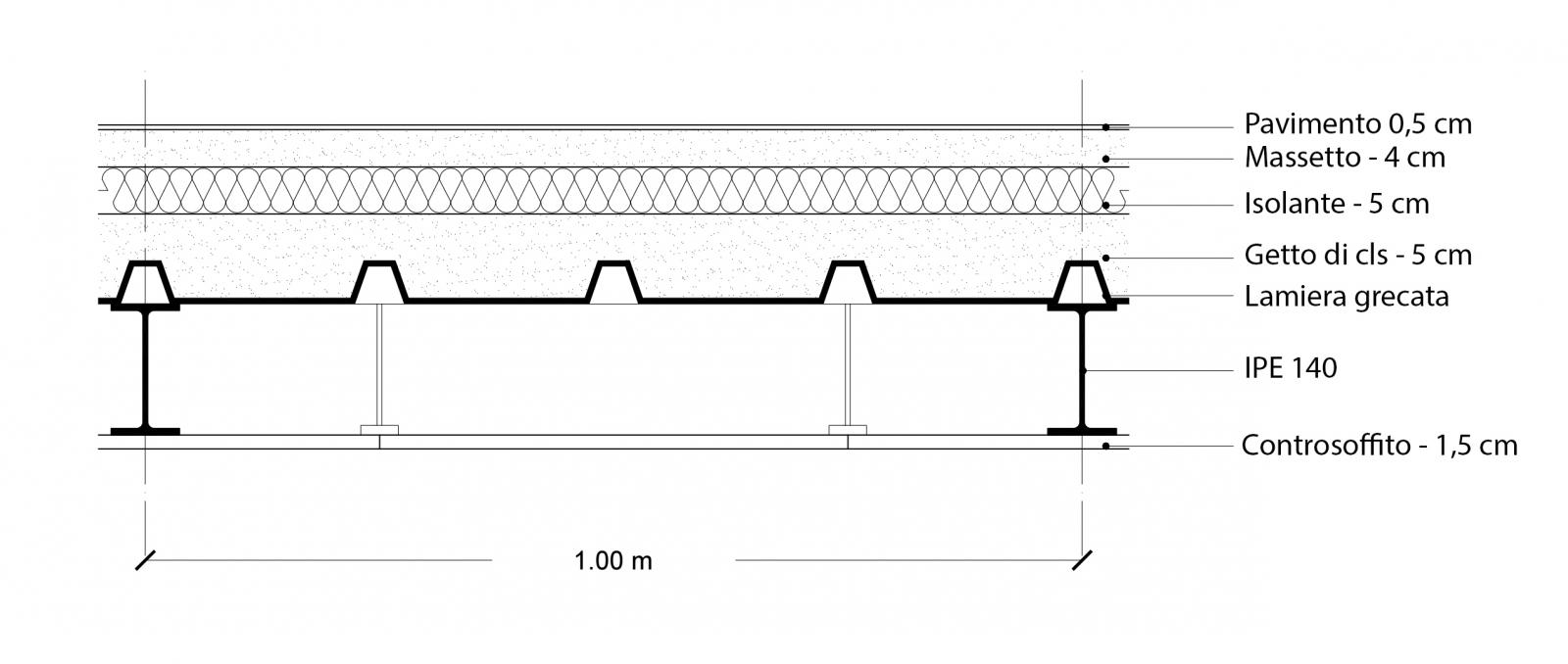
Elementi che compongono il solaio: (f.10)

Travi secondarie: IPE 140 A=16,43 cmq= 0,0016 mq                P = 78,5 kN/mc

Lamiera Grecata: FM 40/1000 spessore 0,6cm                          P = 5,89 kg/mq= 0,0589 kN/mq

Controsoffitto: Knauf D-111 1,5 cm                                          P = 17 kg/mq = 0,17 kN/mq

Getto di cls: 5 cm                                                                      P = 24 kN/mc

Isolante: Lana di roccia 5 cm                                                      P = 30 kg/mc = 0,3 kN/mc

Massetto: 4 cm                                                                           P = 24 kN/mc

Pavimento in resina: 0,5 cm                                                        P = 3,5 kg/mq = 0,035 kN/mq

Calcolo dei carichi strutturali qs (escluso peso proprio della trave)

Travi secondarie

[(0,0016 mq x 1 m)/mq] x (78,5 kN/mc) = (0,0016 mq/mc) x (78,5 kN/mc) = 0,1256 kN/mq

Lamiera Grecata

0,0589 kN/mq

Getto di cls + parte di riempimento della lamiera

[(0,0823 mq x 1 m)/mq] x (24 kN/mc) = (0,0823 mc/mq) x (24 kN/mc) = 1,97 kN/mq

qs = 0,1256 kN/mq + 0,0589 kN/mq + 1,97 kN/mq = 2,15 kN/mq

Calcolo dei carichi portati qp

Controsoffitto

0,17 kN/mq

Isolante

[(0,05 m x 1 m x 1 m)/mq] x (0,3 kN/mc) = (0,05 mc/mq) x (0,3 kN/mc) = 0,015 kN/mq

Massetto

[(0,04 m x 1 m x 1 m)/mq] x (24 kN/mq) = (0,04 mc/mq) x (24 kN/mc) = 0,96 kN/mq

Pavimento in resina

0,035 kN/mq

Impianti

0,5 kN/mq

Tramezzi

1 kN/mq

qp = 0,17 kN/mq + 0,015 kN/mq + 0,96 kN/mq + 0,035 kN/mq + 1 kN/mq + 0,5 kN/mq = 2,68 kN/mq

Calcolo dei carichi accidentali     qa

La struttura è per un ambiente ad uso residenziale (da norma):

qa = 2 kN/mq

Inserisco i dati dei carichi, dell’interasse e della luce nella tabella excel. Considero un fyk= 275 MPa dato il tipo d’acciaio scelto. Risulta un Wxmin=918,15 cmc quindi devo considerare una IPE con il Wx maggiore di 918,15. Prendo il profilato IPE appena più grande IPE 400 con Wx = 1156 cmc. Il pilastro è sovradimensionato in quanto si deve prendere in considerazione il non aver calcolato la trave nei carichi strutturali. (f.11)

f.11

Adesso devo calcolare il peso proprio della trave, come fatto per legno e cls e verificare che il profilato sia verificato.

Il profilato IPE 400 ha un area di 84,46 cmq = 0,008446 mq con un P = 78,5 kN/mc.

Pt= [(0,008446 mq x 1 m)/mq] x (78,5 kN/mc) = (0,008446 mc/mq) x (78,5 kN/mc) = 0,66 kN/mq

Inserisco il peso proprio della trave a qu moltiplicato per 1,3

qu= (qs x 1,3) + (qp x 1,5) + (qa x 1,5) + (Pt x 1,3)

Dopo aver inserito il dato in tabella noto che il coefficiente Wx = 938,21 cmc <1156 cmc.

Posso quindi considerare verificata la mia sezione con profilato IPE 400.