ESERCITAZIONE 3 _ Dimensionamento di una trave a sbalzo

In questa esercitazione verrà pre-dimensionata una mensola e tenendo conto della sua predisposizione a deformarsi sarà necessaria un verifica dell’abbassamento. L’abbassamento massimo della trave più sollecitata non dovrà superare 1/250 della luce.

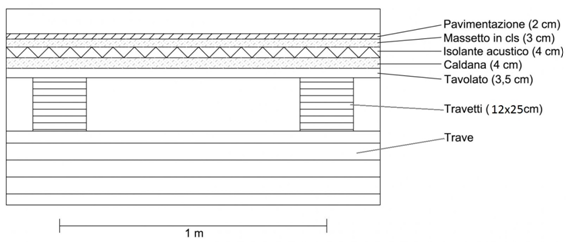
Vengono riportati i carichi calcolati nella prima esercitazione che ricordiamo essere carichi strutturali permanenti q_s , carichi strutturali non permanenti q_p  e i carichi accidentali q_a  nelle tre tecnologie, legno, acciaio e cemento armato.

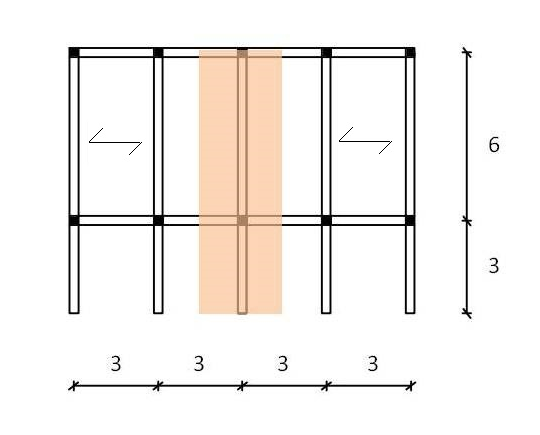Fig.1

TRAVE IN CALCESTRUZZO

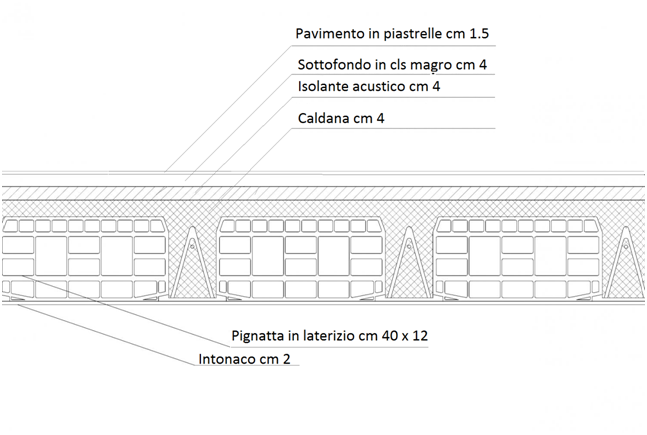Fig. 2

q_s  = 2.12 KN/m²

q_p =  3 KN/m²

q_a = 2 KN/ m²

Con la combinazione di carico allo stato limite ultimo si calcola q_t e tenendo conto della nuova pianta di carpenteria avente luce pari a 3 m e interasse pari a 3 m è possibile calcolare il q_u.

_{COMBINAZIONE DEI CARICHI ALLO SLU:}

q_u =(1.3 x q_s) + ( 1.5 x q_p) + (1.5 x q_a) [KN/ m²] x i [m]

Nel caso della carpenteria mostrata in fig. 1 l’interasse è pari a 3 quindi si trova q_u

q_u =(1.3 x 2.12) + ( 1.5 x 3) + (1.5 x 2) [KN/ m²] x 3 [m] = 30.77 KN/m

Sapendo ch il momento massimo in una mensola è pari a M_max = ql²/2 , è possibile sostituendo il q_u trovato precedentemente, ottenere il M_max riferito al caso in esame.

M_max =30.77 [KN/m]   x 3² [m] /2 = 138.46 KNm

Scelta la resistenza caratteristica dell’acciaio fy_K e la classe di resistenza del calcestruzzo è possibile, fissando la misura della base della trave ed il copriferro, ricavare l’altezza minima.

L’altezza ingegnerizzata della trave in esame sarà quindi pari a 50 cm.

Ora si prosegue con la verifica dell’abbassamento. La verifica si effettua allo Stato Limite di Esercizio poiché riguarda principalmente l’aspetto e la funzionalità della struttura.

Allo SLE i carichi vengono calcolati secondo la combinazione frequente.

q_e = (G₁ + G₂ + Ψ ₁₁ x Q₁ ) x i

Nel caso della struttura in cls è necessario considerare il peso proprio della trave che va aggiunto al peso del solaio.

Inserendo il valore del modulo elastico E = 210000 N/mm²  è possibile trovare lo spostamento massimo V_max .

Se il rapporto l/V_max > 250 la sezione sarà verificata.

TRAVE IN ACCIAIO

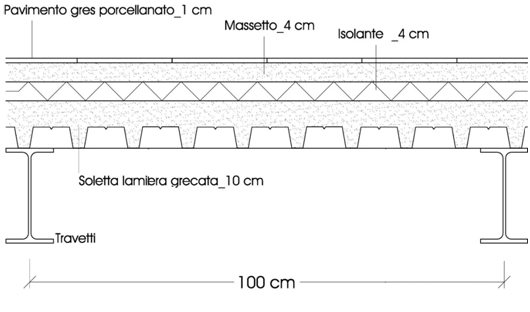  Fig. 3

q_s  = 2.72 KN/m²

q_p =  2.53 KN/m²

q_a = 2 KN/ m²

Con la combinazione di carico allo stato limite ultimo si calcola q_t e tenendo conto della nuova pianta di carpenteria avente luce pari a 3 m e interasse pari a 3 m è possibile calcolare il q_u.

_{COMBINAZIONE DEI CARICHI ALLO SLU:}

q_u =(1.3 x q_s) + ( 1.5 x q_p) + (1.5 x q_a) [KN/ m²] x i [m]

Nel caso della carpenteria mostrata in fig. 1 l’interasse è pari a 3 quindi si trova q_u

q_u =(1.3 x 2.72) + ( 1.5 x 2.53) + (1.5 x 2) [KN/ m²] x 3 [m] = 30.993 KN/m

Sapendo ch il momento massimo in una mensola è pari a M_max = ql²/2 , è possibile sostituendo il q_u trovato precedentemente, ottenere il M_max riferito al caso in esame.

M_max =30.993 [KN/m]   x 3² [m] /2 = 139.46 KNm

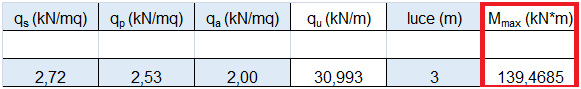
Scelta la classe dell’acciaio f_yk è possibile ricavare il modulo di resistenza a flessione minimo W_{x min.}  

Dal profilario si individua la W_xmin immediatamente superiore a quella trovata e di conseguenza anche il momento di inerzia I_x correlatoVengono inseriti i valori corrispondenti all Ix.

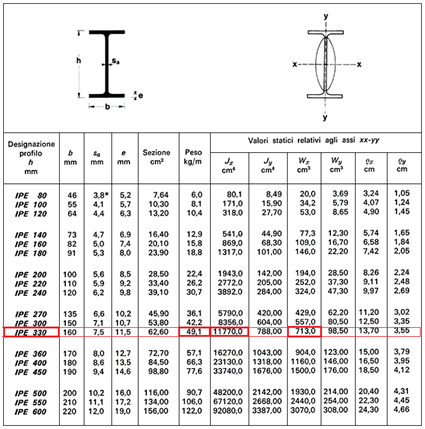
Vengono inseriti i valori corrispondenti a I_x  e al peso della del profilo scelto in questo caso una IPE 330.

Ora si prosegue con la verifica dell’abbassamento.

Allo SLE i carichi vengono calcolati secondo la combinazione frequente.

q_e = (G₁ + G₂ + Ψ ₁₁ x Q₁ ) x i

Anche nel caso della struttura in acciaio è necessario considerare il peso proprio della trave che va aggiunto al peso del solaio.

Se il rapporto l/V_max > 250 la sezione sarà verificata.

TRAVE IN LEGNO

q_s  = 0.39 KN/m²

q_p =  3.07 KN/m²

q_a = 2 KN/ m²

Con la combinazione di carico allo stato limite ultimo si calcola q_t e tenendo conto della nuova pianta di carpenteria avente luce pari a 3 m e interasse pari a 3 m è possibile calcolare il q_u.

_{COMBINAZIONE DEI CARICHI ALLO SLU:}

q_u =(1.3 x q_s) + ( 1.5 x q_p) + (1.5 x q_a) [KN/ m²] x i [m]

Nel caso della carpenteria mostrata in fig. 1 l’interasse è pari a 3 quindi si trova q_u

q_u =(1.3 x 0.39) + ( 1.5 x 3.07) + (1.5 x 2) [KN/ m²] x 3 [m] = 24.336 KN/m

Sapendo ch il momento massimo in una mensola è pari a M_max = ql²/2 , è possibile sostituendo il q_u trovato precedentemente, ottenere il M_max riferito al caso in esame.

M_max =24.336 [KN/m]   x 3² [m] /2 = 109.512 KNm

Si sceglie la dimensione della base e inserendola nella tabella si ricava l’altezza minima della trave che deve essere ingegnerizzata.

Ora si prosegue con la verifica dell’abbassamento. La verifica si effettua allo Stato Limite di Esercizio poiché riguarda principalmente l’aspetto e la funzionalità della struttura.

Allo SLE i carichi vengono calcolati secondo la combinazione frequente.

q_e = (G₁ + G₂ + Ψ ₁₁ x Q₁ ) x i

Nel caso della struttura in legno non è necessario considerare il peso proprio della trave poiché il materiale in quanto leggero non apporta considerevoli modifiche al peso iniziale.

Se il rapporto l/V_max > 250 la sezione sarà verificata.