Esercitazione 3_ dimensionamento di una trave a sbalzo

L’esercitazione si basa sul progetto di una TRAVE A SBALZO

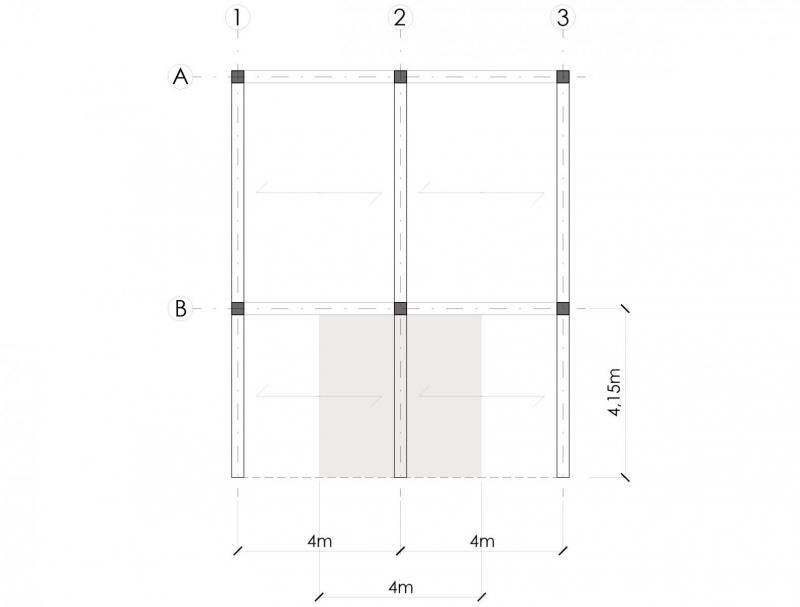
L (luce della trave a sbalzo)= 4.15m                                                                                                                                   I (interasse delle travi)= 4m

La trave più sollecitata è quella lungo il filo fisso 2, poiché l’area di influenza è di 16 mq.

SOLAIO IN ACCIAIO

Dalla precedente esercitazione ho ricavato i carichi del solaio gravanti sulla trave

• carichi strutturali qs = 0.078 + 1.44 +0.45 = 1.97 KN/mq
• carichi permanenti qp = 0.012 + 0.9+ 0.4 +1.5 = 2.81 KN/mq
• carichi accidentali qa = 2.00 KN/mq

Il foglio di calcolo permette di ottenere il valore del carico lineare agente sulla trave  qu

                                  (ricordando che qu =  qtot x A solaio influ trave / L)

Ora siamo in grado di calcolare il Momento massimo della mensola  M=  ql^2 /2  [KNm]

Scelgo il materiale di progetto:    Acciaio S275 con tensione caratteristica di snervamento fyk= 275 [ Mpa]; inserisco il dato sul foglio Excel che calcola la tensione di progetto fyd = fyk/1.05  [Mpa]

Ricavo quindi il valore del Modulo di resistenza a flessione della sezione della trave  Wmin= Mmax/ fyd  [cm^3]

Una volta calcolato Wmin posso consultare la tabella dei profilati  IPE in acciaio scegliendo una sezione con Wx maggiore di quello derivante dal calcolo. Scelta la sezione della trave posso individuare la sua inerzia I ( molto importante nella verifica a deformabilità). La sezione è quindi completamente determinata. Posso inserire nel foglio di calcolo il peso della trave ( KN/m).

Tale procedimento mi ha permesso di progettare una trave con una sezione tale da resistere alle sollecitazioni di progetto (Mmax). Devo però verificare che la deformabilità massima che la trave progettata subisce sia conforme ai limiti imposti dalla normativa (Luce della trave / spostamento max >= 250).

Quando si progetta una sezione a deformabilità la verifica che si deve fare ricade nel campo dello SLE ( stati limite di esercizio): la deformabilità di un elemento infatti non pregiudica la sua funzionalità strutturale ma la possibilità di continuare a svolgere adeguatamente la funzione per cui l’edificio è progettato.

Pertanto devo ricalcolare i carichi agenti sulla trave ( inserendo anche il peso della trave che ora conosco) moltiplicandoli per i coefficienti di sicurezza dello SLE (combinazione dei carichi frequente).

Ora il foglio di calcolo mi permette di ricavare il valore dello spostamento massimo  vmax= qe L^4 /8EIx [cm]

Se tale valore è maggiore uguale a 250 la verifica è soddisfatta; in caso contrario devo cambiare uno o piu parametri che influiscono su Vmax : scegliere una sezione con inerzia più grande oppure diminuire la luce della trave a sbalzo.

SOLAIO IN LEGNO

Dalla precedente esercitazione ho ricavato i carichi del solaio gravanti sulla trave che devono essere maggiorati da coefficienti di sicurezza allo SLU

• carichi strutturali qs = 0.16 + 0.15 = 0.31 KN/mq
• carichi permanenti qp = 1.08 + 0.012 + 0.72+ 0.4 +1.5 = 3.71 KN/mq
• carichi accidentali qa = 2.00 KN/mq

Il foglio di calcolo permette di ottenere il valore del carico lineare agente sulla trave  qu e quindi anche il Mmax.

Scelgo il materiale di progetto:  Legno lamellare GL 32c con resistenza a flessione fmk= 32  [Mpa];            inserisco il dato sul foglio Excel che calcola la tensione di progetto fd =  Kmod  fyk/1.45  [Mpa]

A differenza della trave in acciaio, nel progetto in legno devo imporre per progetto la dimensione di una dei due lati della sezione: impongo la base e ricavo l’altezza che ingegnerizzo.

Ora devo verificare che la trave appena progettata non si deformi troppo. Trascurando il peso proprio della trave, che nel legno è un valore irrilevante, ricalcolo i carichi allo SLE.

Come per la trave in acciaio, ora il foglio di calcolo permette di ottenere il valore dello spostamento massimo Vmax.  La verifica è soddisfatta.

SOLAIO IN CLS

Dalla precedente esercitazione ho ricavato i carichi del solaio gravanti sulla trave che devono essere maggiorati da coefficienti di sicurezza allo SLU

• carichi strutturali qs = 0.76 + 1.20 + 0.73 = 2.69 KN/mq
• carichi permanenti qp = 0.012 + 0.72 + 0.4 + 1.5 + 0.18 + 0.09 = 2.90 KN/mq
• carichi accidentali qa = 2.00 KN/mq

Il foglio di calcolo permette di ottenere il valore del carico lineare agente sulla trave  qu e quindi anche il Mmax.

Scelgo il materiale di progetto:  Acciaio per le armature  B450C con tensione caratteristica  di snervamento     f yk = 450 [Mpa];  inserisco il dato sul foglio Excel che calcola la tensione di progetto fyd= fyk / 1.15 [Mpa]

                                                        Cls  classe  C60/75  con fck = 60 Mpa  da cui  fcd= 0.85 fck / 1.5 [Mpa]

Impongo quindi la dimensione della base della sezione e quella del copri ferro. Devo quindi calcolare l’altezza utile della sezione. Per farlo utilizzo lo stesso procedimento dell’esercitazione 1 calcolando attraverso il foglio Excel i valori di β e r e trovando quindi l’unica incognita hu.

Ricavo il valore dell’altezza minima che andrò ad ingegnerizzare. Ora devo verificare che lo spostamento massimo sia nei limiti consentiti dalla norma. Utilizzo lo stesso procedimento delle precedenti tecnologie.