blog di federica melocchi

RIPARTIZIONE DELLE FORZE SISMICHE

Obbiettivo: calcolo della forza orizzontale ripartita su una struttura costituita da telai

 

Pilastri:  0.30cm x 0.45cm    l(altezza pilastri) = 3.50m

Telaio Av = pilastro 1-5                                   Telaio Ao = pilastro 1-2-3-4

Telaio Av = pilastro 2-6-9                                Telaio Bo = pilastro 5-6-7-8

Telaio Cv = pilastro 3-7-10                              Telaio C0 = pilastro 9-10-11

Telaio Dv = pilastro 4-8-11

Possiamo individuare i telai rappresentandoli come molle (vincoli cedevoli elasticamente)

Calcolo della rigidezza traslante dei telai SHARE- TYPE

• Controventi verticali

k=  12EIx/ l^3 (per ciascun pilastro)       con Ix = bh^3/12 = 0.45 x (0.3)^3/12= 101250 cm4

K(telaio 1-5) = 2 x 12EIx/ l^3= 11902.4 KN/m

K(telaio 2-6-9)= k(telaio 3-7-10)= k(telaio 4-8-11) = 3 x 12EIx/ l^3= 17853 KN/m

• Controventi orizzontali

k=  12EIy/ l^3 (per ciascun pilastro)       con Iy = hb^3/12 = 0.45 x (0.3)^3/12= 227812.5cm4

K(telaio 1-2-3-4)= k(telaio 5-6-7-8) = 4 x 12EIy/ l^3= 53559.2 KN/m

K(telaio 9-10)= 2 x 12EIy/ l^3= 40169.4 KN/m

 

 

 

Calcolo delle distanze dei controventi dal punto O

Si fissa l’origine di un sistema di riferimento e si calcolano le distanze dei controventi ddo, ddv(orizzontali e verticali) da O

Calcolo del centro di massa dell’impalcato

Obbiettivo: calcolo del punto dell’impalcato in cui sarà concentrata la forza sismica

Si divide l’impalcato in figure geometriche semplici di cui calcoliamo l’area e le coordinate del centro di massa (ripetto a O).

[il centro di massa coincide con il centro d’area quando l’impalcato ha massa uniforme]

A1= 36m2    CM= ( 3m, 3m);      A2= 80m2    CM= (13.5m, 6m);     

Il foglio di calcolo permette di ottenere le coordinate del centro di massa dell’intero impalcato

CMtot=  [(x1*A1+ x2*A2) / Atot, (y1*A1+ y2*A2 +)/Atot]

 

Calcolo del centro delle rigidezze dell’impalcato

Obbiettivo: calcolo del braccio della forza sismica che produce una rotazione rigida dell’impalcato.

Il foglio Excel calcola    Kvtot    e    Kotot

CR= [ (kv2* ddv2 + Kvn* ddvn)/ Kvtot , ko2* ddo2 + Kon* ddon)/ Kotot )

Si calcolano anche le distanze d dei controventi (orizzontali e verticali) da CR

Il foglio di calcolo permette di ottenere quindi il valore della rigidezza torsionale totale   Kφ= K*d^2

Kφtot = Kv1*dv1^2 + Kvn*dn^2  + Ko1* do1^2 + Kon*don^2

Analisi dei carichi sismici

Obbiettivo: calcolo della forza sismica concentrata, proporzionale al peso dell’impalcato

Fs (forza sismica) = W(peso edificio) x c      

con W= G +γ x Q

con   G= (qs + qp)x Atot impalcato = (2.69 + 2.9) x 216 KN= 1207,44 KN

con  Q= qa x Atot impalcato = 2.00 x 216 KN= 432 KN

con  γ(coef. Contemporaneità - uffici)= 0.3

W= 1006.2 + 0.3 x 360 KN= 1337 KN

Fs = 4452.15 x 0.15 = 200.6 KN

La forza sismica può colpire l’impalcato orizzontalmente o verticalmente. Dovranno essere analizzate entrambe le ipotesi

• Ripartizione della forza sismica lungo x

Quando la forza sismica agisce in direzione x , sono i controventi ORIZZONTALI a rispondere alla sollecitazione. F produrrà una traslazione orizzontale e una rotazione rigida.

Il foglio Excel calcola gli spostamenti prodotti

U= traslazione orizzontale = F / Kotot      U= 200.6 KN / ktot KN/m= 0.001m

La rotazione rigida è trascurabile. Pertanto le forze reattive alla forza sismica saranno prodotte dai soli controventi orizzontali.

F1= F2= 72.93 KN      F3= 54.7 KN

 

 

• Ripartizione della forza sismica lungo y

Quando la forza sismica agisce in direzione y , sono i controventi VERTICALI a rispondere alla sollecitazione. F produrrà una traslazione verticale e una rotazione rigida.

V= traslazione verticale=  F / Kvtot      v= 200.6 KN / ktot KN/m= 0.003m

La rotazione rigida è trascurabile. Pertanto le forze reattive alla forza sismica saranno prodotte dai soli controventi verticali.

F1= 36.46 KN          F2=F3=F4 54.7 KN

 

L’esercitazione prevede il dimensionamento dei pilastri di un piccolo edificio di 5 piani, progettato nelle tre tecnologie: cls, acciaio e legno.

 

Lp(trave principale)= 6m

Ls/(trave secondaria)=4m

Npiani= 5

Il dimensionamento prenderà in considerazione il pilastro più sollecitato: il pilastro del piano terra con area d’influenza 6mx4m (pilastro B2)

I pilastri sono elementi strutturali sottoposti a sforno normale di compressione: la loro tendenza è quella di sbandare lateralmente.

CLS

Per dimensionare correttamente il pilastro si deve tenere conte del peso proprio delle travi (principali e secondarie) che il peso del solaio in un mq, ricavando poi il peso totale dell’area d’influenza che il pilastro devo sopportare.

Peso unitario trave principale = (0.3mx0.5m) x 25KN/mc= 3.75 KN/m

Peso unitario trave secondaria = 3.75 KN/m

Il foglio di calcolo permette di ottenere il peso delle travi:

trave p= 3.75 KN/m x 6.00m x 1.3 (è un carico strutturale permanente)= 29.25 KN

trave s= 3.75KN/m x 4.00m X 1.3= 19.5 KN

qtrave= 48.75 KN

 

Ora bisogna aggiungere il carico del solaio (esercitazione1)

qs= 2.70 KN/mq

qp= 2.90 KN/mq

qa= 2.00 KN/mq

area d’influenza= 24mq

qsolaio= (1.3 x 2.70 + 1.5 x 2.90 + 1.5 x 2) KN/mq x 24mq = 260.64 KN

Una volta trovati i carichi che agiscono sul pilastri posso ricavare il valore dello sforzo normale agente sul pilastro più sollecitato del piano terra. Questo pilastro sarà soggetto alla sollecitazione derivante dai piani sovrastanti ( 5 piani).

N= 5 x (260.64 + 48.75)KN= 1547KN

Scelgo il materiale (nel progetto del pilastro in cls posso trascurare l’acciaio, considero una sezione omogenea di cls)

fck=  60MPa

fcd= 0.85x fck /1.5= 34 Mpa

il foglio Excel calcola l’area minima= N/fcd= 455 cmq

Una volta trovata l’area minima devo capire cose essa deve essere distribuita: posso decidere che la sezione del pilastro è quadrata

bmin= radq Amin = 21.3cm

 

ora devo considerare i valori che entrano in gioco per il calcolo dell’instabilità

E= 21000 Mpa     l(altezza del pilastro)= 3.50m   β(dipende dal vincolo: appoggio/appo)=1

 

Posso quindi definire la snellezza del pilastro:

λ= π x radq(E/fcd)= 78.08

 

posso trovare il raggio d’inerzia minimo:

ρ= βl/λ= 1 x 3.50 /78.08m =4.48cm

ricalcolo la base minima conoscendo il raggio minimo d’inerzia:

bmin= ρmin/ radq 12  (sapendo che ρmin= radq (Imin/Amin)

bmin= 4.48cm x radq12= 15.53cm

ora posso ingegnerizzare la sezione: 40 x40 cm con Hmin= Amin/b= 15.53cm

 

Infine attraverso il foglio Excel posso trovare altri valori correlati alla geometria della sezione.

Per verificare che il dimensionamento sia corretto è necessario che σmax < fcd

σmax è la tensione generata dallo sforzo normale di compressione e dal momento flettente che le travi trasmettono al pilastro (c’è un incastro)

σmax= N/A + M/Wmax= 21.89MPa < 34Mpa= fcd

 

 

ACCIAIO

Il dimensionamento del pilastro in acciaio segue lo stesso procedimento di quello in cls. Le travi principali e secndarie sono IPE 360 con un peso unitario di 0.57KN/m

Calcolo il peso strutturale delle travi    qtrave= 1.3x ( 6.00x0.57 + 4.00x0.57 )= 7.41KN

Riporto i dati dell’esercitazione 1 sui carichi del solaio i acciaio:

qs= 1.97KN/m

qp=2.81KN/m

qa=2.00KN/m

scelgo la classe dell’acciaio  fyk= 275MPa

dopo aver trovare il raggio d’inerzia minimo posso scegliere una sezione con ρ più grande. Il profilo scelto è HEA 160. Il dimensionamento termina con la verifica della sezione: la snellezza del pilastro deve essere inferiore a 250.

λ= βxl /ρmin = 87.94 < 250 

LEGNO

Il peso unitario delle travi è di 0.82 KN/m

qs= 0.31KN/m

qp= 3.71KN/m

qa= 2,00KN/m

scelgo la classe del legno   fck= 21 Mpa

il foglio di calcolo permette di ottenere il valore di Amin= 975 cm2; posso ingegnerizzare la base e l’altezza min maggiorando quella ricavata dal foglio Excel. La sezione sarà 35x35 cm. La sezione è verificata se Adesign> Amin

Amin= 975cm2 < Adesign= 1225 cm2

L’esercitazione si basa sul progetto di una TRAVE A SBALZO

L (luce della trave a sbalzo)= 4.15m                                                                                                                                   I (interasse delle travi)= 4m

La trave più sollecitata è quella lungo il filo fisso 2, poiché l’area di influenza è di 16 mq.

SOLAIO IN ACCIAIO

Dalla precedente esercitazione ho ricavato i carichi del solaio gravanti sulla trave

• carichi strutturali qs = 0.078 + 1.44 +0.45 = 1.97 KN/mq
• carichi permanenti qp = 0.012 + 0.9+ 0.4 +1.5 = 2.81 KN/mq
• carichi accidentali qa = 2.00 KN/mq

 

Il foglio di calcolo permette di ottenere il valore del carico lineare agente sulla trave  qu

                                  (ricordando che qu =  qtot x A solaio influ trave / L)

Ora siamo in grado di calcolare il Momento massimo della mensola  M=  ql^2 /2  [KNm]

Scelgo il materiale di progetto:    Acciaio S275 con tensione caratteristica di snervamento fyk= 275 [ Mpa]; inserisco il dato sul foglio Excel che calcola la tensione di progetto fyd = fyk/1.05  [Mpa]

Ricavo quindi il valore del Modulo di resistenza a flessione della sezione della trave  Wmin= Mmax/ fyd  [cm^3]

Una volta calcolato Wmin posso consultare la tabella dei profilati  IPE in acciaio scegliendo una sezione con Wx maggiore di quello derivante dal calcolo. Scelta la sezione della trave posso individuare la sua inerzia I ( molto importante nella verifica a deformabilità). La sezione è quindi completamente determinata. Posso inserire nel foglio di calcolo il peso della trave ( KN/m).

Tale procedimento mi ha permesso di progettare una trave con una sezione tale da resistere alle sollecitazioni di progetto (Mmax). Devo però verificare che la deformabilità massima che la trave progettata subisce sia conforme ai limiti imposti dalla normativa (Luce della trave / spostamento max >= 250).

Quando si progetta una sezione a deformabilità la verifica che si deve fare ricade nel campo dello SLE ( stati limite di esercizio): la deformabilità di un elemento infatti non pregiudica la sua funzionalità strutturale ma la possibilità di continuare a svolgere adeguatamente la funzione per cui l’edificio è progettato.

Pertanto devo ricalcolare i carichi agenti sulla trave ( inserendo anche il peso della trave che ora conosco) moltiplicandoli per i coefficienti di sicurezza dello SLE (combinazione dei carichi frequente).

Ora il foglio di calcolo mi permette di ricavare il valore dello spostamento massimo  vmax= qe L^4 /8EIx [cm]

Se tale valore è maggiore uguale a 250 la verifica è soddisfatta; in caso contrario devo cambiare uno o piu parametri che influiscono su Vmax : scegliere una sezione con inerzia più grande oppure diminuire la luce della trave a sbalzo.

SOLAIO IN LEGNO

Dalla precedente esercitazione ho ricavato i carichi del solaio gravanti sulla trave che devono essere maggiorati da coefficienti di sicurezza allo SLU

• carichi strutturali qs = 0.16 + 0.15 = 0.31 KN/mq
• carichi permanenti qp = 1.08 + 0.012 + 0.72+ 0.4 +1.5 = 3.71 KN/mq
• carichi accidentali qa = 2.00 KN/mq

Il foglio di calcolo permette di ottenere il valore del carico lineare agente sulla trave  qu e quindi anche il Mmax.

Scelgo il materiale di progetto:  Legno lamellare GL 32c con resistenza a flessione fmk= 32  [Mpa];            inserisco il dato sul foglio Excel che calcola la tensione di progetto fd =  Kmod  fyk/1.45  [Mpa]

A differenza della trave in acciaio, nel progetto in legno devo imporre per progetto la dimensione di una dei due lati della sezione: impongo la base e ricavo l’altezza che ingegnerizzo.

Ora devo verificare che la trave appena progettata non si deformi troppo. Trascurando il peso proprio della trave, che nel legno è un valore irrilevante, ricalcolo i carichi allo SLE.

Come per la trave in acciaio, ora il foglio di calcolo permette di ottenere il valore dello spostamento massimo Vmax.  La verifica è soddisfatta.

SOLAIO IN CLS

Dalla precedente esercitazione ho ricavato i carichi del solaio gravanti sulla trave che devono essere maggiorati da coefficienti di sicurezza allo SLU

• carichi strutturali qs = 0.76 + 1.20 + 0.73 = 2.69 KN/mq
• carichi permanenti qp = 0.012 + 0.72 + 0.4 + 1.5 + 0.18 + 0.09 = 2.90 KN/mq
• carichi accidentali qa = 2.00 KN/mq

Il foglio di calcolo permette di ottenere il valore del carico lineare agente sulla trave  qu e quindi anche il Mmax.

Scelgo il materiale di progetto:  Acciaio per le armature  B450C con tensione caratteristica  di snervamento     f yk = 450 [Mpa];  inserisco il dato sul foglio Excel che calcola la tensione di progetto fyd= fyk / 1.15 [Mpa]

                                                        Cls  classe  C60/75  con fck = 60 Mpa  da cui  fcd= 0.85 fck / 1.5 [Mpa]

Impongo quindi la dimensione della base della sezione e quella del copri ferro. Devo quindi calcolare l’altezza utile della sezione. Per farlo utilizzo lo stesso procedimento dell’esercitazione 1 calcolando attraverso il foglio Excel i valori di β e r e trovando quindi l’unica incognita hu.

Ricavo il valore dell’altezza minima che andrò ad ingegnerizzare. Ora devo verificare che lo spostamento massimo sia nei limiti consentiti dalla norma. Utilizzo lo stesso procedimento delle precedenti tecnologie.

La seconda esercitazione si basa sul dimensionamento di una travatura reticolare tridimensionale composta da aste sottoposte a trazione o compressione.  Per  riuscire a dimensionare questo elemento strutturale occorre utilizzare il programma SAP e il foglio di calcolo Excel.

Operazioni:

• Cliccare su file, new model, grid only selezionando una griglia su cui disegnare la reticolare
• Draw frame per disegnare le diverse aste che compongono la struttura. Decido di realizzare una struttura reticolare composta da cubi che dovranno essere controventati  su tutte le facce. Copiando la singola campata realizzo l’intera struttura.
• Seleziono i punti su cui mettere i vincoli; clicco su assign, join, restraint  per scegliere il tipo di vincoli.  (Vicoli scelti 4 cerniere)
• Selezionando l’intera struttura clicco su assign, frame, release: devo capire quali spostamenti sono ammissibile dal vincolo precedentemente scelto: nel mio caso la cerniera permette la rotazione, clicco quindi su Moment =0
• Clicco su assign, frame, frame sections, add new property, selezionando il materiale per le aste (steel, pipe)
• Nell’analisi delle sollecitazioni trascuro il peso proprio della struttura: define, load patterns, creo un nuovo elemento (A) inserendo 0 nel self weight
• Selezionando solo le facce superiori clicco assign, joint loads, forces (assegno carichi concentrati lungo l’asse z).
• Ora che la struttura è caricata posso far iniziare l’analisi, capendo come le aste rispondono alle sollecitazioni di trazione o compressione: run analysis, selezionando solo l’elemento da me creato (A).
• Clicco sul telaio show deformed shape per vedere la deformazione dell’elemento strutturale.
• Ora che ho le sollecitazioni devo esportare i dati sul foglio Excel: display, show tables, analysis result, select patterns, selezionando l’elemento da me creato A. esporto la tabella su Excel.

 

 

Dimensionamento delle aste tese

Dalla tabella esportata da SAP si è in grado di stabilire i valori di progetto degli sforzi di trazione N

Scelta del materiale: Acciaio S235 con tensione caratteristica di snervamento fyk= 235 Mpa. Con il foglio di calcolo si ottiene il valore della tensione di progetto fyd= fyk/1.05 Mpa

Conoscendo le caratteristiche del materiale e le sollecitazione si ottiene automaticamente il valore dell’area minima Amin= N/fyd [cm^2]. Sono ora in grado di ingegnerizzare la sezione. Decido di scegliere solo 2 dimensioni delle aste tubolari cave per una maggiore semplificazione: 4.53 cm^2 e  12.30 cm^2

 

 

Dimensionamento delle aste compresse

Stabiliti i valori di progetto degli sforzi di compressione e il materiale ( acciaio S235) posso procedere al dimensionamento delle aste compresse.

Dopo aver calcolato automaticamente l’area minima Amin (come il precedente caso)devo considerare nuovi parametri che entrano in gioco nell’instabilità delle aste compresse.

β è il parametro che dipende dal grado di vincolo. In questo caso β= 1 (asta doppiamente appoggiata)

L è la lunghezza delle aste ( paramento che influenza maggiormente l’instabilità): L= 4m e  L=5.65m ( per controventi)

 λ è la snellezza dell’elemento; è direttamente proporzionale a E (modulo di elasticità, nell’acciaio              E=210000 Mpa  e inversamente proporzionale alla tensione di progetto fyd

ρ è il rapporto tra la lunghezza di libera inflessione (β x L) e la snellezza λ

Imin è l’inerzia minima che la sezione deve avere Imin= Amin x ρ^2

Tutti questi valori sono calcolati automaticamente dal foglio Excel.

Ora posso ingegnerizzare la sezione andando a scegliere un’inerzia maggiore a quella calcolata. Come per il precedente caso, scelgo solo 2 dimensioni di profilo. La normativa impone che la snellezza λ= βL/ ρ  <200. La verifica è soddisfatta.

 

 

 

 

 

 

 

 

 

 

 

 

 

L’esercitazione prevede il dimensionamento della trave più sollecitata di un solaio nelle tre tecnologie: acciaio, legno, cls.

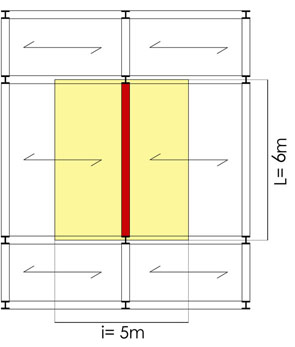
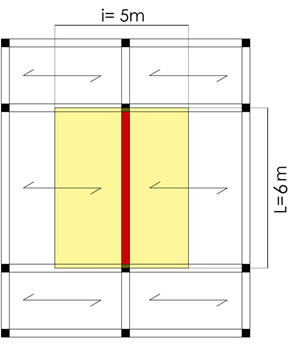
Si analizza quindi la trave di luce 6m più sollecitata con un’area d’influenza pari a 30 mq ( L di 6m x i di 5m).

SOLAIO IN ACCIAIO

 

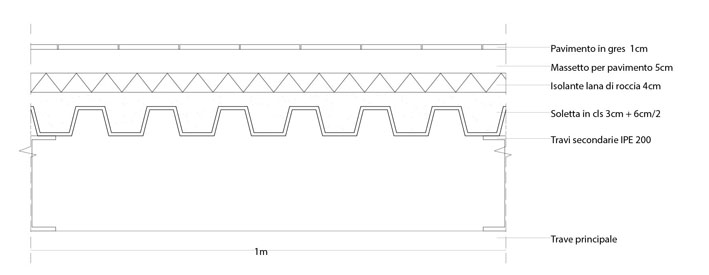
Carichi strutturali permanenti ( qs )  (ancora non tengo conto del peso della trave di cui non ne conosco le dimensioni)                            

                                                            

• Lamiera grecata         carico del materiale unif. distribuito su1mq di  solaio  = 7.85 kg/mq
• Soletta in cls                                              peso specifico di1mc di materiale = 24 KN/mc
• Travi secondarie (IPE 200)                     peso specifico di 1mc di materiale = 78.5 KN/mc

Carichi non strutturali permanenti ( qp )                

• Isolante lana di roccia                                 peso specifico di 1mc di materiale = 30 kg/mc
• Massetto pavimenti                                peso specifico di 1mc di materiale = 1800 kg/mc
• Pavimento in gres         carico del materiale unif. distribuito su 1mq di  solaio  = 40 kg/mq
• Tramezzi /impianti     carico tram. /impianti unif. distribuito su 1mq di solaio = 1.5 KN/mq

Carichi accidentali (qa)

• Carico di esercizio residenziale                                                                       2.00 KN/mq

ANALISI DEI CARICHI

     MATERIALE          SPESSORE          PESO UNITARIO            CARICO UNIF. DISTRIBUITO

•  Lamiera grecata                             7.85 kg/mq           7.85 /100 Kg/mq = 0.078KN/mq 
• Soletta in cls (0.03m+0.06/2m)mq   24 KN/mc   0.06 mc/mq x24 KN/mc = 1.44 KN/mq
•  Travett0   0.00285 mc           78.5 KN/mc   0.0057 mc/mq x 78.5 KN/mc =0.22 KN/mq

---

• Isolante    0.04mx1m x1m         30 kg/mc        0.04mc/mq x 0.3 KN/mc= 0.012 KN/mq
• Massetto   0.05 x1m x1m       1800 kg/mc           0.05 mc/mq x 18 KN/mc = 0.9 KN/mq   
• Pavimento                                 40 Kg/mq                           40/100 kg/mq = 0.4 KN/mq
•  Tramezzi /Impianti                                                                                        1.5 KN/mq

---

•  Carico d’esercizio                                                                                         2.00 KN/mq

Si calcolano i carichi totali ( maggiorati attraverso coefficienti di sicurezza nelle verifiche allo SLU):

• carichi strutturali qs = 0.078 + 1.44 +0.22 = 1.74 KN/mq
• carichi permanenti qp = 0.012 + 0.9+ 0.4 +1.5 = 2.81 KN/mq
• carichi accidentali qa = 2.00 KN/mq

Inserisco i carichi trovati(qs, qp, qa) nel foglio Excel che calcola il carico lineare sulla trave qu.

qtot = qs x 1.3 + qp x 1.5 + qa x 1.5           

qtot = 1.74 x 1.3 + 2.81 x1.5 + 2.0 x1.5 = 9.47 KN/mq (carico unif. distribuito su un mq  di solaio)                                                                                                                                     

A me serve il carico lineare agente sulla trave ( modello trave di Bernoulli).

Operazioni: 

- dal carico distribuito su un mq di solaio devo calcolare il carico distribuito sulla superficie del solaio d’influenza della trave:   qarea solaio influenza trave = qtot x A solaio influenza trave.

- dal carico distribuito sulla trave tridimensionale devo passare al modello  bidimensionale di Bernoulli (carico lineare [ KN/m]): q lineare sulla trave= qtot x A solaio influ trave / L

A influenza solaio = L x i      A = 6m x 5m = 30 mq  

 qu (lineare trave) = 9.47 KN/mq x 30 mq / 6m = 47.35 KN/m

Si può calcolare il momento massimo sulla trave in esame doppiamente appoggiata prodotto dal carico linearmente distribuito appena calcolato.

Mmax = qu (lineare trave ) x L^2  / 8         M max = 47.35KN/m x 36 mq / 8 = 213.08 KNm

Si sceglie la classe dell’acciaio della trave: acciaio S275

con tensione caratt. di snervamento f yk = 275 Mpa inserendola nel foglio di calcolo

f yk = 27.5 KN/cmq          f yd ( tensione snervamento progetto) = f yk / γs         

f yd = 27.5 / 1.05 KN/cmq = 26.19 KN/cmq (calcolata automaticamente dal foglio di calcolo).

Il foglio di calcolo permette di ottenere automaticamente  W x,min  per  scegliere l’IPE ( modulo di resistenza a flessione della sezione)

W x,min = Mmax / f yd           W x,min =  21308 KNcm / 26.19 KN/cmq = 813.59 cm3   

IPE 360  Wx  = 904 cm3

Ora che conosco le dimensioni della trave devo aggiungere il suo peso ai carichi strutturali permanenti.    IPE 360 peso di in metro di trave: 57.1 kg/m = 0.57 KN/m                                    

Aggiorno l’analisi dei carichi aggiungendo a quelli strutturali il peso della trave, verificando se la trave è in grado si resistere ai nuovi carichi complessivi.

q u = 9.47 KN/mq x 5m + 0.57 KN/m x 1.3 = 48.10 KN/m

M max = 48.10 KN/m x 36 mq / 8 = 216.45 KNm

W x,min =  21645 KNcm / 26.19 KN/cmq = 826.46 cm3   il modulo di resistenza a flessione della trave ricalcolata è minore di quello della trave di progetto, quindi la scelta dell’IPE 360 è corretta. 

 

SOLAIO IN LEGNO

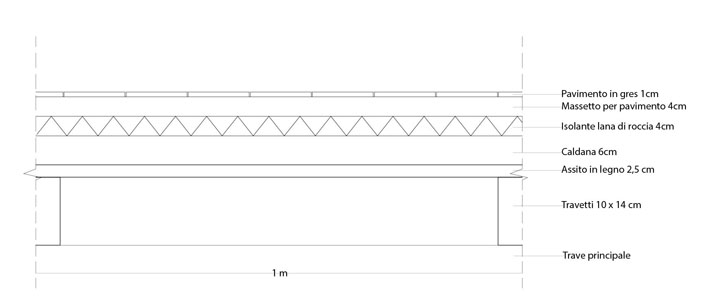
Carichi strutturali permanenti ( qs )

(ancora non tengo conto del peso della trave di cui non ne conosco le dimensioni)                                                              

• Travetti                                                  peso specifico di un mc di materiale = 6 KN/mc
• Assito in legno                                        peso specifico di un mc di materiale = 6 KN/mc

Carichi non strutturali permanenti ( qp )                

• Caldana                                             peso specifico di un mc di materiale = 1800 kg/mc
• Isolante lana di roccia                             peso specifico di un mc di materiale = 30 kg/mc
• Massetto pavimenti                            peso specifico di un mc di materiale = 1800 kg/mc
• Pavimento in gres                        carico  unif. distribuito su un mq di  solaio  = 40 kg/mq
• Tramezzi/impianticarico   tramezzi/ impianti unif. distribuito su1mq di solaio = 1.5 KN/mq

Carichi accidentali (qa)

• Carico di esercizio residenziale                                                                       2.00 KN/mq  

ANALISI DEI CARICHI

     MATERIALE         SPESSORE    PESO UNITARIO             CARICO UNIF. DISTRIBUITO

• Travetti   (0.10m x0.14m x1m)   6 KN/mc    0.014 mc/mq x 6 KN/mc  = 0.084 KN/mq
• Assito in legno  0.025mx1mx1m  6 KN/mc       0.025 mc/mq x 6 KN/mc = 0.15 KN/mq

---

• Caldana    0.06mx1mx1m      1800 kg/mc       0.06 mc/mq x  18 KN/mc = 1.08 KN/mq
•  Isolante   0.04mx1mx1m          30 kg/mc       0.04mc/mq x 0.3 KN/mc= 0.012 KN/mq
• Massetto   0.04mx1mx1m      1800 kg/mc        0.04 mc/mq x 18 KN/mc = 0.72 KN/mq 
• Pavimento                                  40 Kg/mq                         40/100 kg/mq = 0.4 KN/mq
• Tramezzi/Impianti                                                                                      0.15 KN/mq

---

•  Carico d ’esercizio                                                                                      2.00 KN/mq                                                                                                             

                                                     

Si calcolano i carichi totali ( maggiorati attraverso coefficienti di sicurezza nelle verifiche allo SLU):

• carichi strutturali qs = 0.084 + 0.15 = 0.23 KN/mq
• carichi permanenti qp = 1.08 + 0.012 + 0.72+ 0.4 +1.5 = 3.71 KN/mq
• carichi accidentali qa = 2.00 KN/mq

Inserisco i carichi trovati(qs, qp, qa) nel foglio Excel che calcola il carico lineare sulla trave q u.

q u =  44.32 KN/m

Si può calcolare il momento massimo sulla trave in esame doppiamente appoggiata prodotto dal carico linearmente distribuito appena calcolato.

Mmax = qu (lineare trave ) x L^2  / 8         M max = 44.32 KN/m x 36 mq / 8 = 199.44 KNm

Si sceglie la classe del legno della trave: legno lammellare GL 32c

con resistenza a flessione  f mk = 32 Mpa inserendola nel foglio di calcolo

f mk = 3.2 KN/cmq          f yd ( tensione  progetto) = k mod f mk / γm         f yd = 0.8 x 3.2 / 1.45 KN/cmq = 1.76 KN/cmq (calcolata automaticamente dal foglio di calcolo).

Per ricavare l’altezza della trave occorre imporre la dimensione della base b= 25 cm. Conoscendo le caratteristiche del materiale e la tensione di progetto l’altezza è l’unica incognita. Per l’equazione Wmin = Mx / fyd derivante dalla formula di Navier ,Wmin (resistenza a flessione della trave) è l’incognita. Posso calcolare Wmin per una sezione rettangolare.

Wmin= (bh^2 )/6       h^2min =  6 Mx / fd x b       hmin =   52.07 cm   ingegnerizzando la sezione si impone h = 55 cm.

Nel progetto della trave non si è tenuto conto del suo peso. Ora , una volta trovate le caratteristiche geometriche della trave, occorre verificare se il progetto è corretto. Aggiungo quindi il peso della trave ai carichi strutturali.

Peso di un metro di trave:  (0.25 x 0.55 x 1)mc/m x 6 KN/mc = 0.82 KN/m

q u = 44.32 KN/m + 0.82 KN/m x 1.3 = 45.39 KN/m          M max= 204.24 KNm    

hmin = 52.69cm

Pertanto la sezione progettata (25 x 55 cm) è corretta.

 

 

SOLAIO IN LATEROCEMENTO

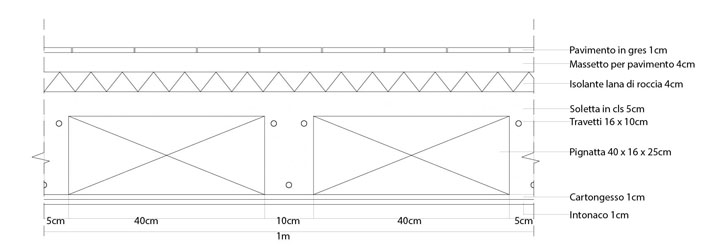
Carichi strutturali permanenti ( qs )                               

(ancora non tengo conto del peso della trave di cui non ne conosco le dimensioni)                            

                                                           

• Travetti in cls                                              peso specifico di 1mc di materiale = 24 KN/mc
• Soletta collaborante in cls                           peso specifico dic1mc di materiale = 24 KN/mc
• Pignatta                                                                 peso specifico di 1pignatta = 9.1kg/cad

Carichi non strutturali permanenti ( qp )                

• Isolante                                                         peso specifico di 1mc di materiale = 30 kg/mc
• Massetto pavimento                                   peso specifico di 1mc di materiale = 1800 kg/mc
• Pavimento in gres             carico del materiale unif. distribuito su 1mq di  solaio = 40 kg/mq
• Tramezzi/impianti      carico  tramezzi/impianti unif. distribuito su1mq di solaio = 1.5 KN/mq
• Cartongesso                                                 peso specifico di 1mc di materiale = 900 kg/mc
• Intonaco                                                       peso specifico di 1mc di materiale = 18 KN/mc

Carichi accidentali (qa)

• Carico di esercizio residenziale                                                                            2.00 KN/mq

 

ANALISI DEI CARICHI

     MATERIALE               SPESSORE        PESO UNITARIO         CARICO UNIF. DISTRIBUITO

•  Travetti in cls   2x(0.16mx0.1mx1m) 24 KN/ mc    0.032mc/mq x 24 KN/mc= 0.76 KN/mq
•   Soletta in cls    0.05m x 1m x 1m      24 KN/mc     0.05 mc/mq x 24 KN/mc = 1.20 KN/mq
•   Pignatta             8 pignatte/ mq              9.1 Kg                    8/ mq x 9.1 kg = 0.73 KN/mq

---

• Isolante          0.04m x 1m x 1m         30 kg/mc    0.04mc/mq x 0.3 KN/mc= 0.012 KN/mq
• Massetto        0.04m x 1m x 1m       1800 kg/m      0.04 mc/mq x 18 KN/mc = 0.72 KN/mq
•  Pavimento                                         40 Kg/mq                        40/100 kg/mq = 0.4 KN/mq
•  Tramezzi/Impianti                                                                                               1.5 KN/mq
• Cartongesso       0.01mx1mx1m        900 kg/mc                0.01mc/mq x 9KN= 0.09 KN/mq
•  Intonaco        0.01m x 1m x 1m        18 KN/mc                     0.01x18KN/mc= 0.18 KN/mq 

---

• Carico d’esercizio                                                                                               2.00 KN/mq

Si calcolano i carichi totali ( maggiorati attraverso coefficienti di sicurezza nelle verifiche allo SLU):

• carichi strutturali qs = 0.76 + 1.20 + 0.73 = 2.69 KN/mq
• carichi permanenti qp = 0.012 + 0.72 + 0.4 + 1.5 + 0.18 + 0.09 = 2.90 KN/mq
• carichi accidentali qa = 2.00 KN/mq

Inserisco i carichi trovati(qs, qp, qa) nel foglio Excel che calcola il carico lineare sulla trave q u.

q u (lineare trave) = 54.24 KN/m

M max = 54.24KN/m x 36 mq / 8 = 244.06 KNm

Dopo aver analizzato i carichi del solaio la procedura per il progetto della trave in cls armato è differente rispetto a quella in acciaio e legno.

La trave in cls armata è composta da due materiali: l’acciaio per le armature che rispondono alla trazione e  il cls che risponde a compressione. Occorre quindi scegliere la classe dei due materiali.

Acciaio per le armature:  B450C con tensione caratt. di snervamento f yk = 450 Mpa  

                                             f yd = 45 / 1.15 KN/cmq = 39.13 KN/cmq

cls:   classe C60/75  con    fck = 60 Mpa      f cd= 0.85 x 60 / 1.5 Mpa = 3.4 KN/cmq  

Fisso una base arbitraria della sezione della trave di progetto: b= 20 cm e copriferro= 4 cm

Sapendo che:

β= fcd  / (fcd + fyd/n) = 0.57        con n (coef. omogeneizzazione) = 15        xc = β x hu

Calcolo il braccio della coppia di forze ( risultante del cls compresso e risultante dell’acciaio teso che generano un M)

B= hu –xc/3 = (1 – β/3) x hu

 

Ora che conosco il braccio delle due forze posso calcolare il M prodotto.

M = fcd x  xc x b/2 x (1 – β/3) x hu     M è noto (momento di progetto della trave doppiamente appoggiata). La sola incognita è hu  (calcolata con l’equazione dal foglio di calcolo).

hu =  39.54 cm

ingegnerizzo la sezione H = 45 cm

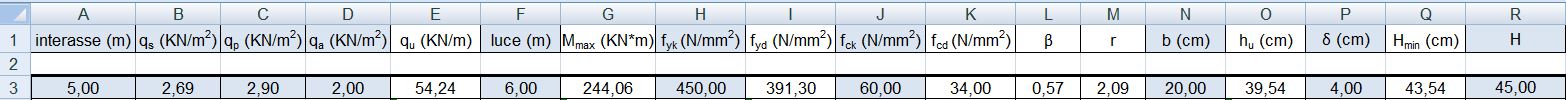
Una volta ingegnerizzato la sezione è nota la sua geometria (20 x 45 cm). Il foglio Excel calcola il peso unitario della trave (2.25 KN/m) e aggiunge tale peso specifico ai carichi strutturali verificando che la sezione progettata supporti anche il peso proprio.

La nuova sezione ( calcolata tenendo conto del peso della trave) deve avere un’altezza minima di 44.59 cm.  La sezione di progetto da me ingegnerizzata è di 45 cm. La sezione è quindi verificata.

ciao a tuttiiiiii!!!!!