Esercitazione 4_ dimensionamento pilasto

L’esercitazione prevede il dimensionamento dei pilastri di un piccolo edificio di 5 piani, progettato nelle tre tecnologie: cls, acciaio e legno.

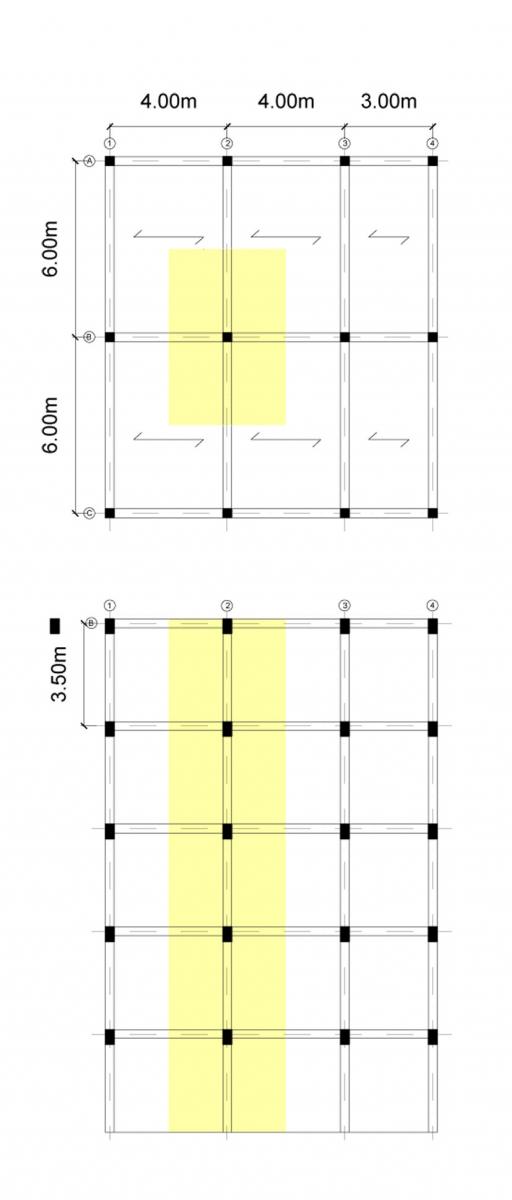
Lp(trave principale)= 6m

Ls/(trave secondaria)=4m

Npiani= 5

Il dimensionamento prenderà in considerazione il pilastro più sollecitato: il pilastro del piano terra con area d’influenza 6mx4m (pilastro B2)

I pilastri sono elementi strutturali sottoposti a sforno normale di compressione: la loro tendenza è quella di sbandare lateralmente.

CLS

Per dimensionare correttamente il pilastro si deve tenere conte del peso proprio delle travi (principali e secondarie) che il peso del solaio in un mq, ricavando poi il peso totale dell’area d’influenza che il pilastro devo sopportare.

Peso unitario trave principale = (0.3mx0.5m) x 25KN/mc= 3.75 KN/m

Peso unitario trave secondaria = 3.75 KN/m

Il foglio di calcolo permette di ottenere il peso delle travi:

trave p= 3.75 KN/m x 6.00m x 1.3 (è un carico strutturale permanente)= 29.25 KN

trave s= 3.75KN/m x 4.00m X 1.3= 19.5 KN

qtrave= 48.75 KN

Ora bisogna aggiungere il carico del solaio (esercitazione1)

qs= 2.70 KN/mq

qp= 2.90 KN/mq

qa= 2.00 KN/mq

area d’influenza= 24mq

qsolaio= (1.3 x 2.70 + 1.5 x 2.90 + 1.5 x 2) KN/mq x 24mq = 260.64 KN

Una volta trovati i carichi che agiscono sul pilastri posso ricavare il valore dello sforzo normale agente sul pilastro più sollecitato del piano terra. Questo pilastro sarà soggetto alla sollecitazione derivante dai piani sovrastanti ( 5 piani).

N= 5 x (260.64 + 48.75)KN= 1547KN

Scelgo il materiale (nel progetto del pilastro in cls posso trascurare l’acciaio, considero una sezione omogenea di cls)

fck=  60MPa

fcd= 0.85x fck /1.5= 34 Mpa

il foglio Excel calcola l’area minima= N/fcd= 455 cmq

Una volta trovata l’area minima devo capire cose essa deve essere distribuita: posso decidere che la sezione del pilastro è quadrata

bmin= radq Amin = 21.3cm

ora devo considerare i valori che entrano in gioco per il calcolo dell’instabilità

E= 21000 Mpa     l(altezza del pilastro)= 3.50m   β(dipende dal vincolo: appoggio/appo)=1

Posso quindi definire la snellezza del pilastro:

λ= π x radq(E/fcd)= 78.08

posso trovare il raggio d’inerzia minimo:

ρ= βl/λ= 1 x 3.50 /78.08m =4.48cm

ricalcolo la base minima conoscendo il raggio minimo d’inerzia:

bmin= ρmin/ radq 12  (sapendo che ρmin= radq (Imin/Amin)

bmin= 4.48cm x radq12= 15.53cm

ora posso ingegnerizzare la sezione: 40 x40 cm con Hmin= Amin/b= 15.53cm

Infine attraverso il foglio Excel posso trovare altri valori correlati alla geometria della sezione.

Per verificare che il dimensionamento sia corretto è necessario che σmax < fcd

σmax è la tensione generata dallo sforzo normale di compressione e dal momento flettente che le travi trasmettono al pilastro (c’è un incastro)

σmax= N/A + M/Wmax= 21.89MPa < 34Mpa= fcd

ACCIAIO

Il dimensionamento del pilastro in acciaio segue lo stesso procedimento di quello in cls. Le travi principali e secndarie sono IPE 360 con un peso unitario di 0.57KN/m

Calcolo il peso strutturale delle travi    qtrave= 1.3x ( 6.00x0.57 + 4.00x0.57 )= 7.41KN

Riporto i dati dell’esercitazione 1 sui carichi del solaio i acciaio:

qs= 1.97KN/m

qp=2.81KN/m

qa=2.00KN/m

scelgo la classe dell’acciaio  fyk= 275MPa

dopo aver trovare il raggio d’inerzia minimo posso scegliere una sezione con ρ più grande. Il profilo scelto è HEA 160. Il dimensionamento termina con la verifica della sezione: la snellezza del pilastro deve essere inferiore a 250.

λ= βxl /ρmin = 87.94 < 250 

LEGNO

Il peso unitario delle travi è di 0.82 KN/m

qs= 0.31KN/m

qp= 3.71KN/m

qa= 2,00KN/m

scelgo la classe del legno   fck= 21 Mpa

il foglio di calcolo permette di ottenere il valore di Amin= 975 cm2; posso ingegnerizzare la base e l’altezza min maggiorando quella ricavata dal foglio Excel. La sezione sarà 35x35 cm. La sezione è verificata se Adesign> Amin

Amin= 975cm2 < Adesign= 1225 cm2