Dimensionamento di una travatura reticolare tridimensionale _ Esercitazione 2

Questa seconda esercitazione si basa sul dimensionamento di una travatura reticolare tridimensionale. Attraverso il software SAP2000 è possibile disegnare la struttura e vincolarla esternamente tramite quattro appoggi.

Trattandosi di una struttura reticolare possiamo modellizzare i nodi come delle cerniere interne.

Una volta scelto il materiale (acciaio) e i profili delle sezioni (circolari cavi) sono state applicate forze concentrate sui nodi superiori della travatura.

 Il software permette di visualizzare la struttura deformata e i grafici relativi allo sforzo normale: in rosso le aste compresse (puntoni), in blu le aste tese (tiranti).

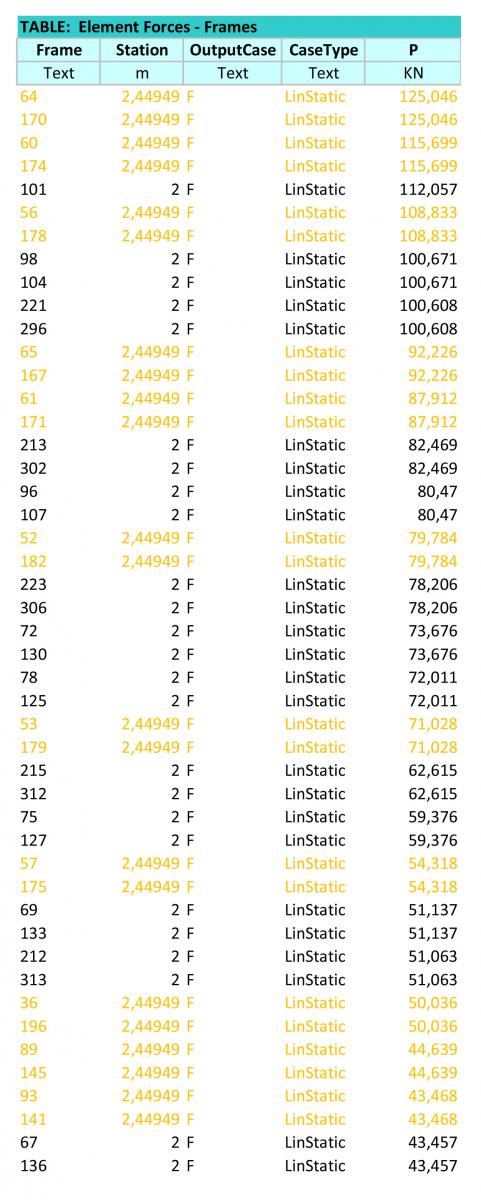
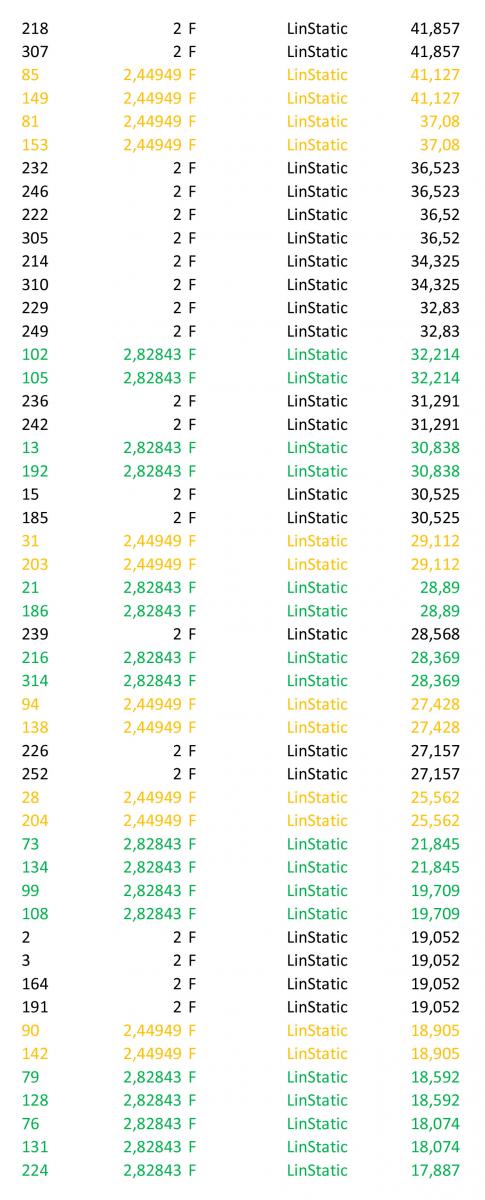
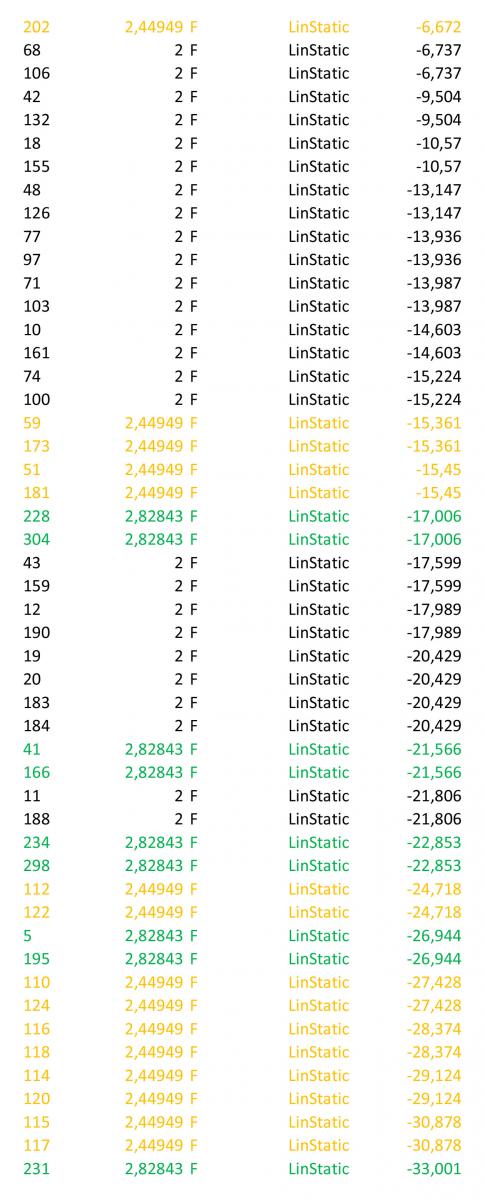
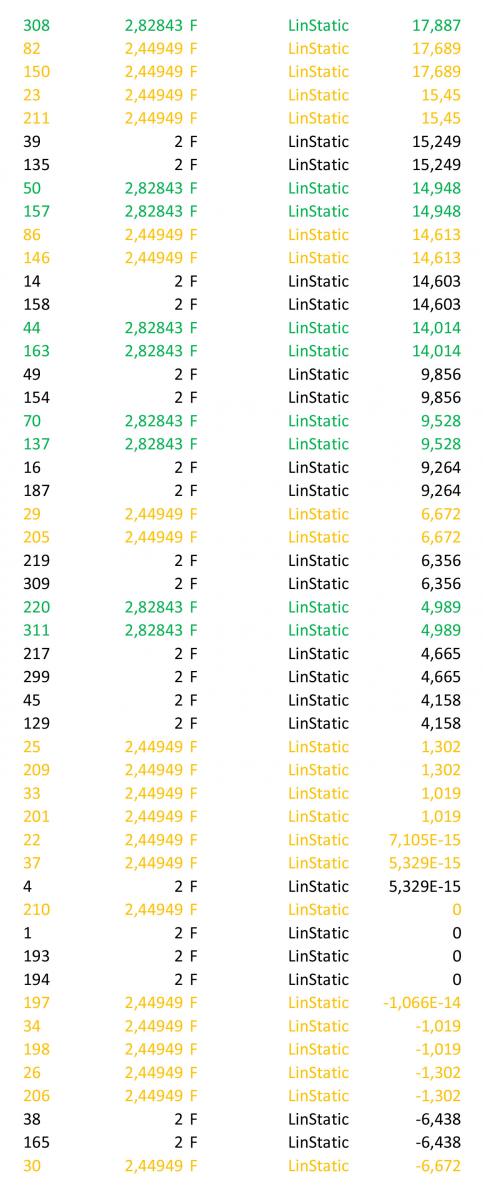
 È possibile poi esportare i valori numerici degli sforzi assiali delle singole aste in una foglio di calcolo.

Innanzitutto il file va pulito mantenendo solo i valori di station pari alla lunghezza effettiva dell’asta. Dunque nel caso di questa struttura è necessario mantenere le aste di 2m che corrispondono ai lati del quadrato di base (nere); le aste lunghe 2.82m che corrispondono alle diagonali dei quadrati di base (verde); le aste lunghe 2.44m che corrispondo ai lati della piramide (arancio).

Quindi è possibile ordinare la tabella in funzione dello sforzo normale dal valore maggiore al valore minore e quindi si possono individuare facilmente le aste più tese nella struttura (valori maggiori con segno positivo) e quali quelle più compresse (valori maggiori con segno negativo).

TRAZIONE

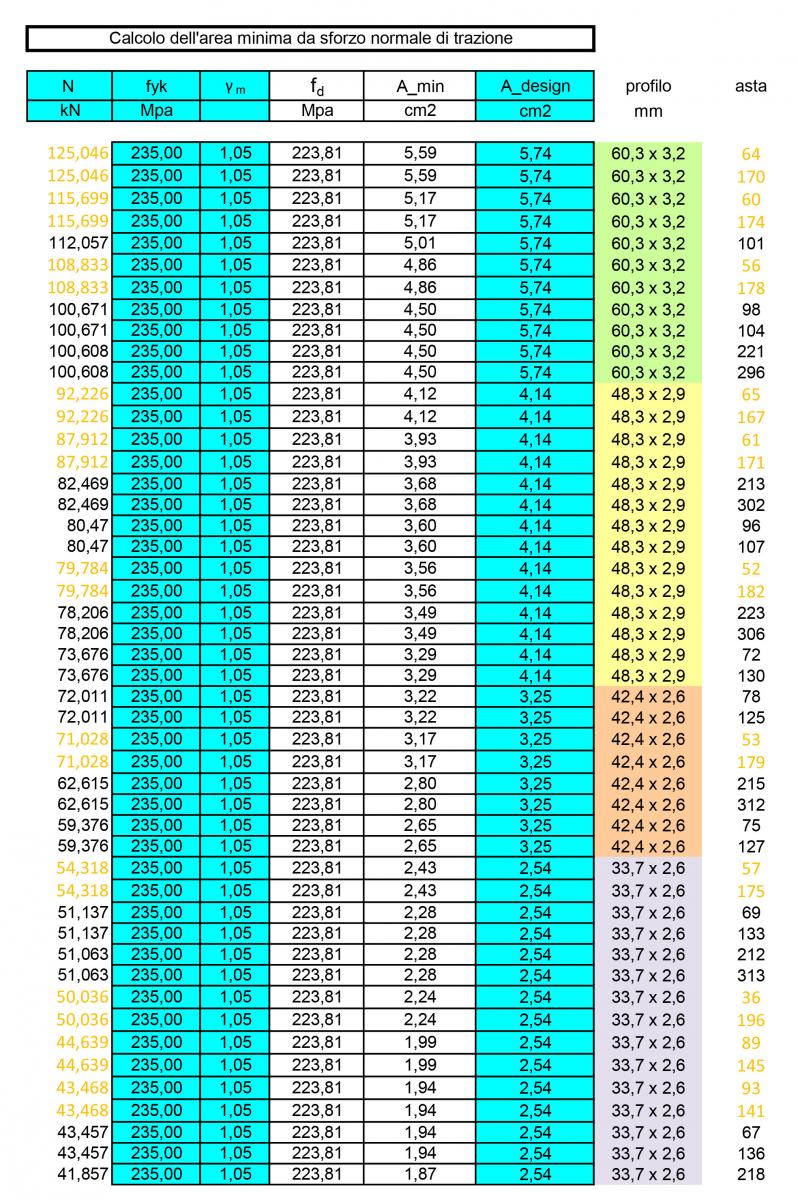
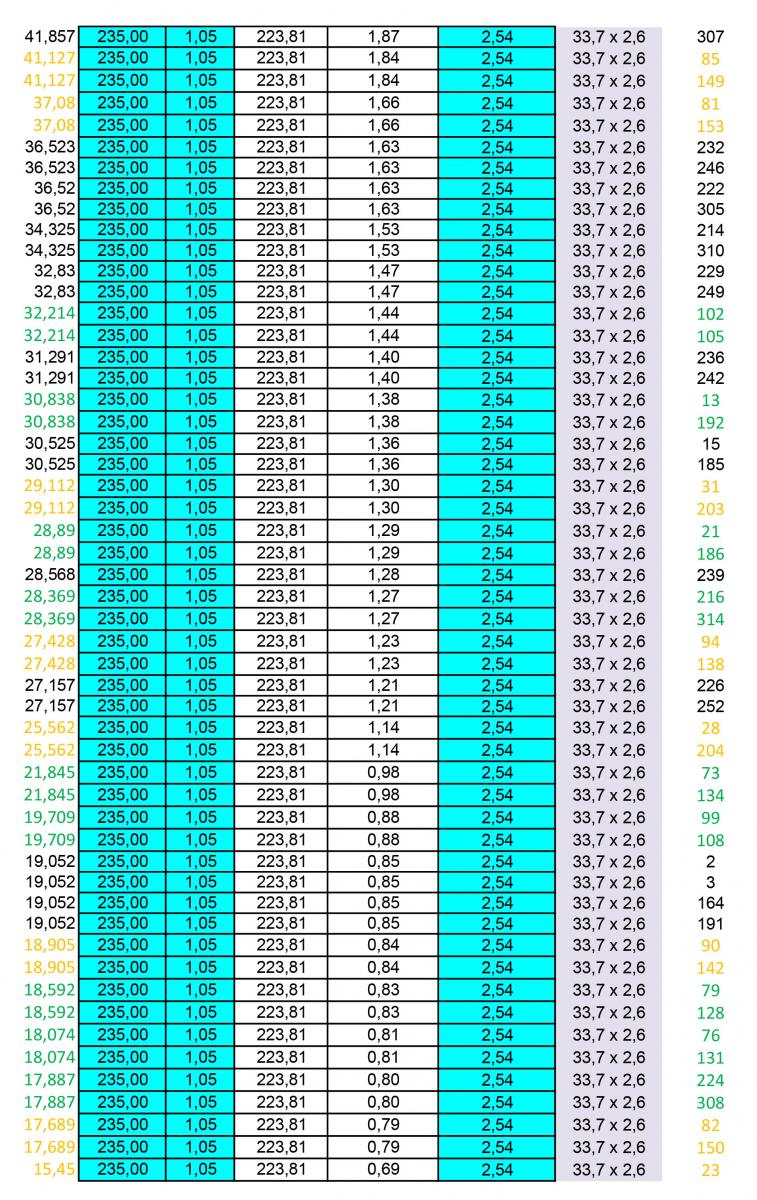
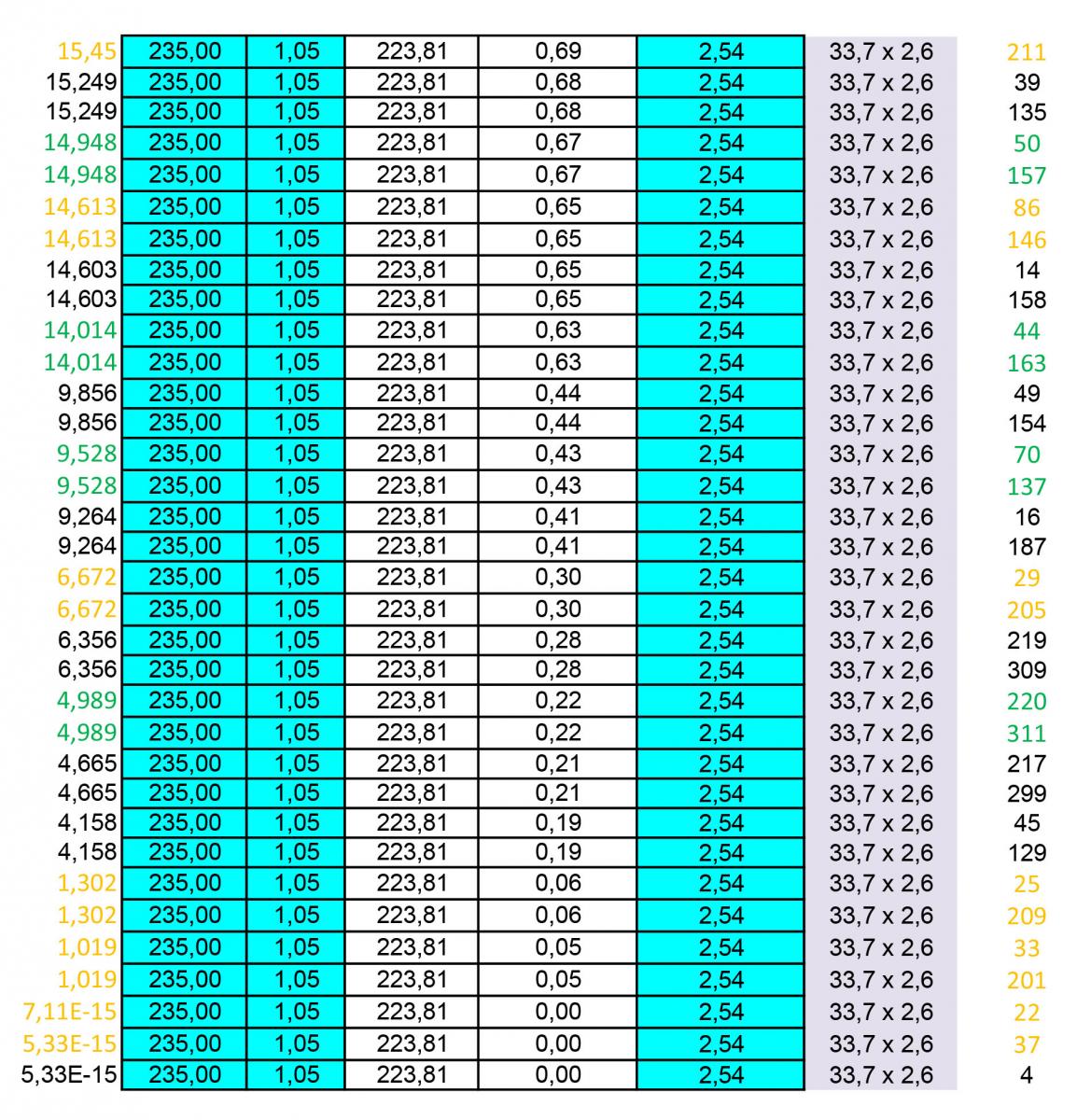
Un ulteriore foglio di calcolo ci permetterà di dimensionare i profili circolari cavi per le aste tese.

Infatti, una volta inseriti i valori degli sforzi normali e scelto il tipo di acciaio (un acciaio S235 con resistenza caratteristica fyk = 235 Mpa), il foglio calcolerà la resistenza di progetto fd correggendo quella caratteristica con un coefficiente di sicurezza γm=1.05 e l’area minima dividendo lo sforzo normale per la resistenza di progetto appena calcolata

Amin = N/fd

Infatti abbiamo imposto che σ=fd.

Consultando la tabella dei profilati circolari cavi dovremmo scegliamo il profilo con area immediatamente maggiore per ciascuna asta, ma ciò comporterebbe un eccessivo costo e difficoltà di montaggio nella realizzazione della reticolare. Dunque si scelgono 4 profili che soddisfino le aree minime delle aste tese. Si aggiungono dunque due nuove colonne con il tipo di profilo scelto e il numero di asta corrispondente.

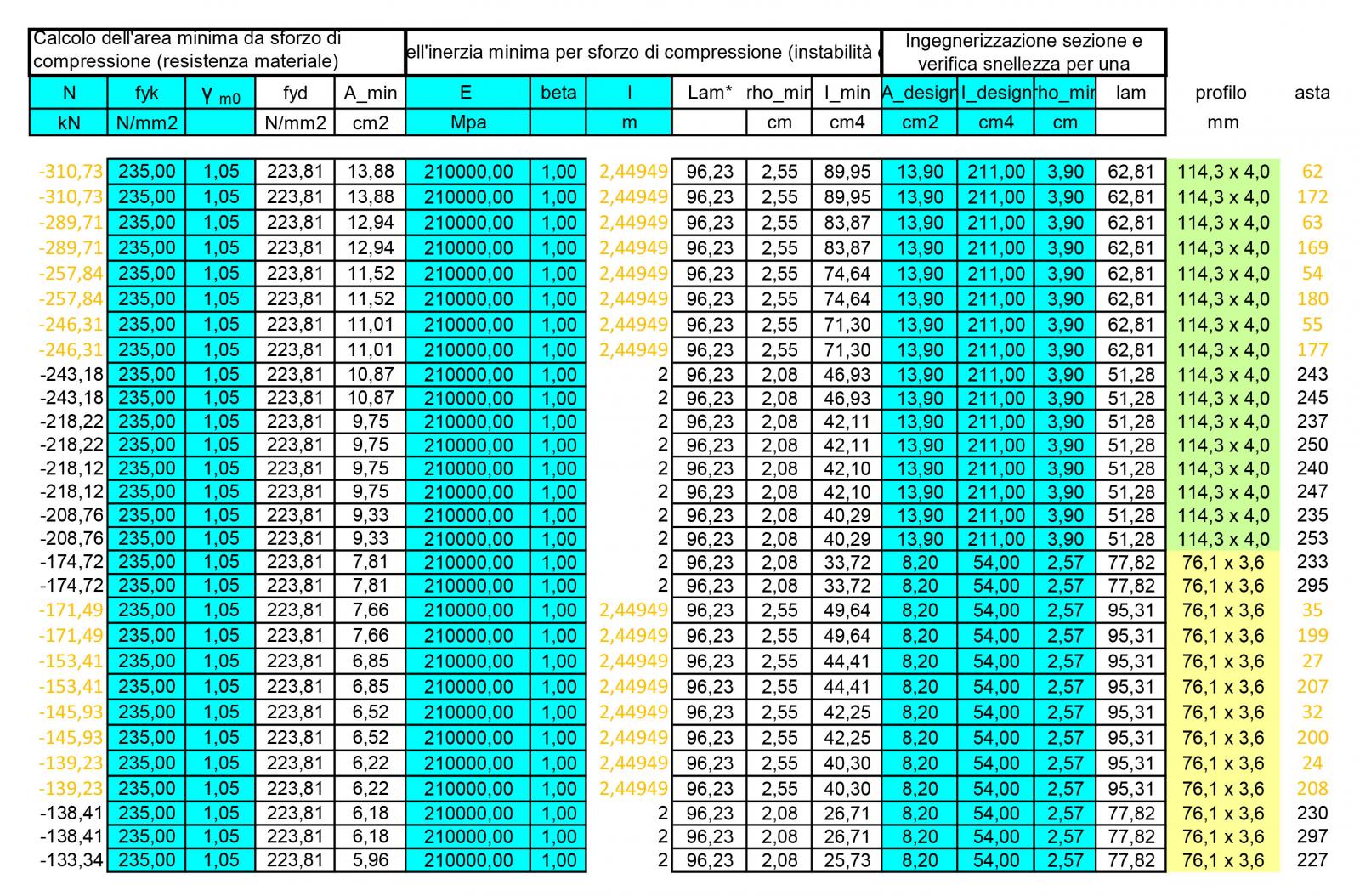
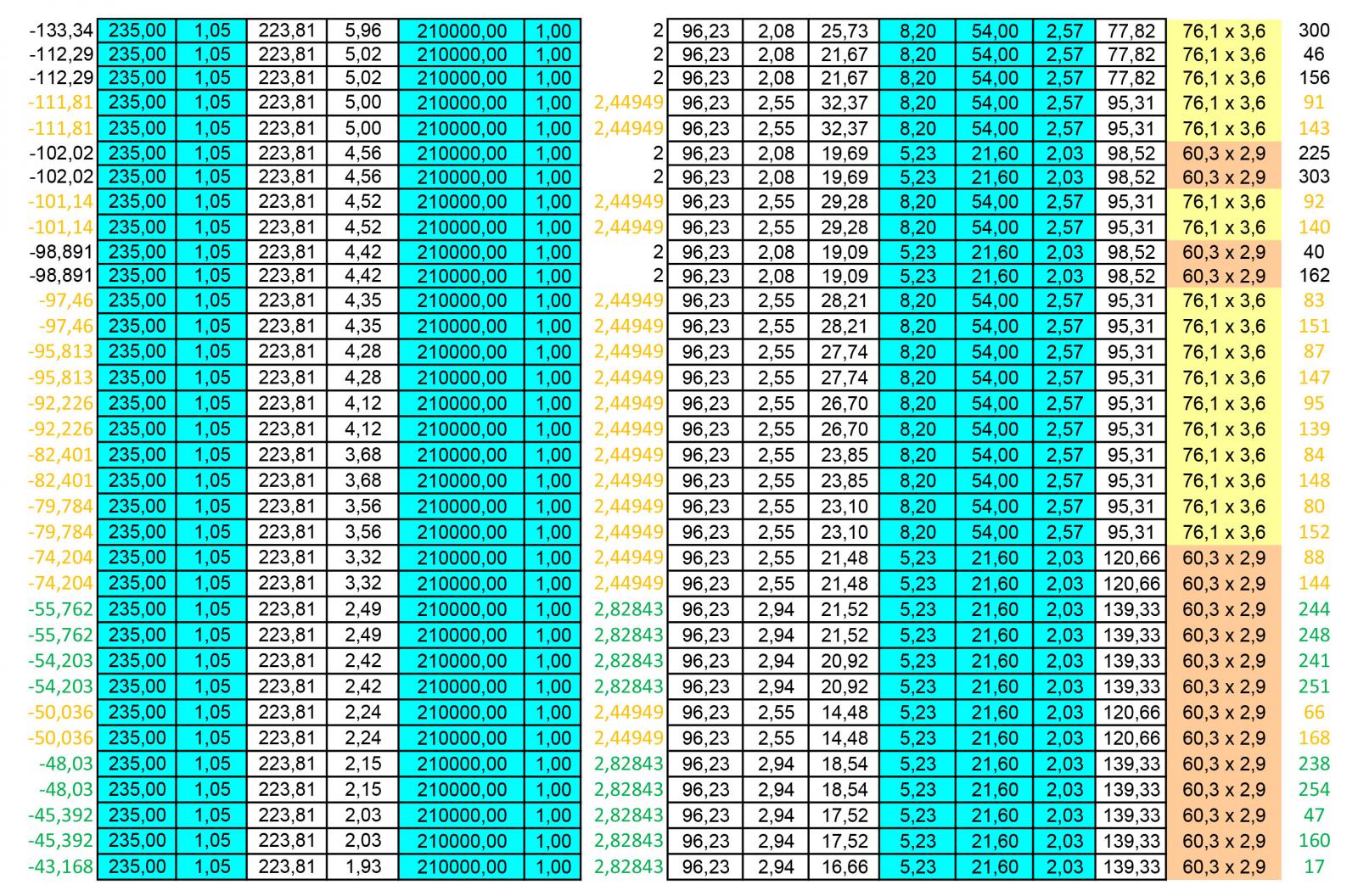
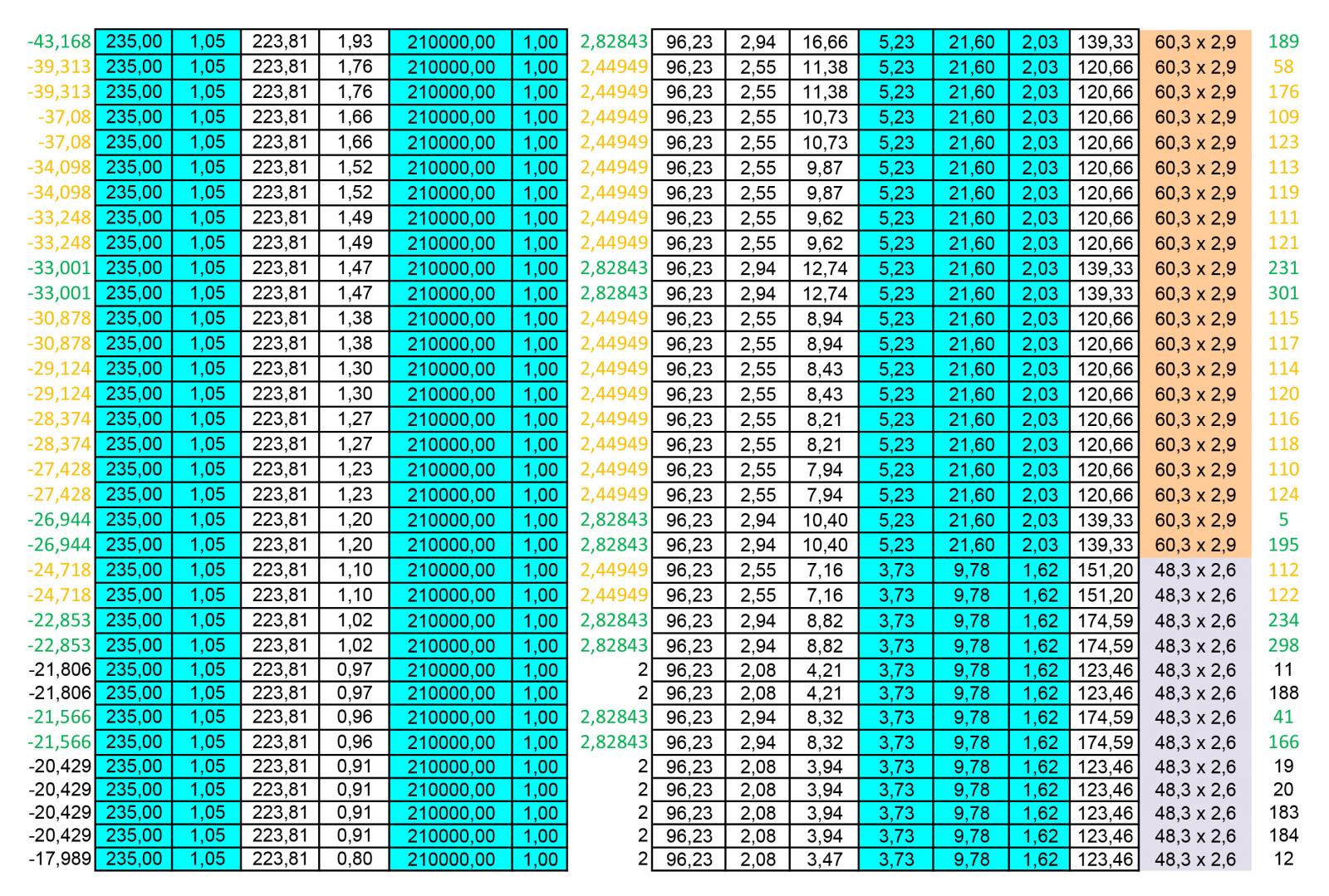
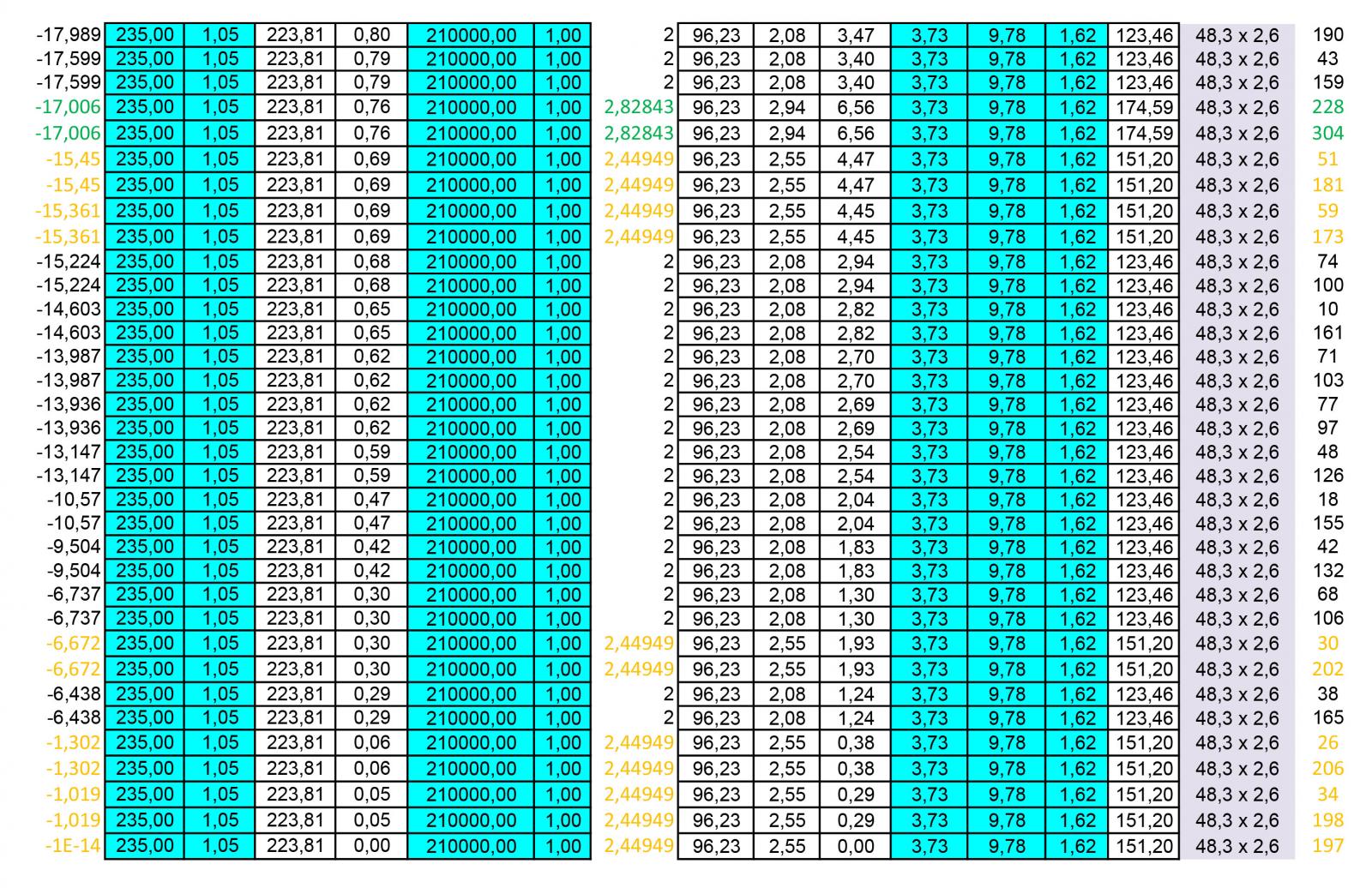
COMPRESSIONE

Un ulteriore foglio di calcolo ci permetterà di dimensionare i profili circolari cavi per le aste compresse.

Come nel caso della trazione, una volta inserito lo sforzo normale e il tipo di acciaio, è possibile ricavare la resistenza di progetto e dunque l’area minima imponendo nuovamente σ=fd.

Amin = N/fd

Nel caso della compressione, però, dobbiamo considerare anche l’instabilità euleriana. Dunque sarà necessario imporre σcrit = fd.

fd = σcrit = Ncrit/A = (π²E)/λ²

dunque λ = π/√(E/fyd)

Dove E è il modulo di elasticità dell’acciaio pari a 210000Mpa. Nella tabella possiamo aggiungere due ulteriori valori noti: β = 1 (trattandosi di un asta incernierata) e le luci delle aste. Con questi nuovi dati possiamo calcolare ρmin.

ρmin = L0/ λ

dove L0= β x l

Ora sapendo che ρmin²=Imin/A

Imin = ρmin²/A

Consultando la tabella dei profilati circolari cavi dovremmo scegliere il profilo con area e momento di inerzia immediatamente maggiori per ogni asta. Come per quelle tese sarà necessario scegliere un numero di profili limitati per semplificare il montaggio e ammortizzare i costi: sono stati scelti dunque 4 profili che soddisfino le aree e le inerzie minime delle aste compresse controllando che la snellezza λ sia inferiore di 200. Si aggiungono dunque due nuove colonne con il tipo di profilo scelto e il numero di asta corrispondente.