blog di Silvia_Mezzetti

La quinta esercitazione consiste nel calcolo della ripartizione di una forza orizzontale (sismica o del vento) agente su una struttura a telai Shear-Type in cemento armato utilizzando il metodo delle rigidezze.

La struttura presa in analisi è caratterizzata da 3 telai orizzontali e 4 telai verticali e i pilastri sono di dimensioni 30x50cm, di altezza 3,50m.

I controventi sono per il solaio vincoli cedevoli elasticamente quindi vengono rappresentati nel piano dell’impalcato come molle di adeguata rigidezza.

STEP1

Poichè i telai sono modellizzati come degli Shear-Type sappiamo che ogni ritto contribuirà alla rigidezza traslante con un contributo di 12EI/h³.

K=(12EI₁)/ h³ + (12EI₂) h³+ … + (12EI_n)/h³

Quindi per calcolare la rigidezza traslante di ogni controvento sarà necessario inserire nel foglio excel il modulo di Young proprio del materiale(E), l’altezza dei pilastri (h) e il loro modulo d’inerzia (I):

Imax=bh³/12=(30cm)*(50cm)³/12= 312500cm⁴

Imin= hb³/12=(50cm)*(30cm)³/12= 112500cm⁴

STEP2

In questo step vengono calcolate le distanze dei controventi dal punto O, origine del sistema di riferimento.

STEP3

Per il calcolo del centro di massa è necessario suddividere l’impalcato in figure elementari, calcolare le rispettive aree e individuare le coordinate del loro centro geometrico. Dunque sarà possibile calcolare il centro di massa (che nel caso di un impalcato con densità di massa uniforme coincide con il centro d’area)

XG = [(A₁ * x_G1)+(A₂ * x_G2)]/Atot

YG = [(A₁ * y_G1)+(A₂ * y_G2)]/Atot

STEP4

Oltre a calcolare la rigidezza totale orizzontale (k_otot) e verticale(k_vtot), il foglio di calcolo ricava le coordinate del centro delle rigidezze

XC = [(k_v1*d_v1)+ (k_v2*d_v2)+ (k_v3*d_v3)+ (k_v4*d_v4)]/k_vtot

YC = [(k_o1*d_o1)+ (k_o2*d_o2)+ (k_o3*d_o3)]/k_otot

Ora è dunque possibile rappresentare nell’impalcato il centro di massa G e il centro delle rigidezze C.

Sapendo che la forza sismica verrà applicata al centro di massa, possono essere fatte delle osservazioni.

Se la forza sismica è orizzontale allora l’impalcato trasla di una quantità u e ruota in modo antiorario.

Se la forza sismica è verticale allora l’impalcato trasla di una quantita v e ruota in modo antiorario.

In questo step vengono inoltre ricalcolate le distanze dei controventi dal centro di rigidezza per ricavare la rigidezza torsionale k_φ

k_φ = (k_v1*dd_v1²)+ (k_v2*dd_v2²)+ (k_v3*dd_v3²)+ (k_v4*dd_v4²)+(k_o1*dd_o1²)+ (k_o2*dd_o2²)+ (k_o3*dd_o3²)

STEP5

Inserendo i valori dei carichi strutturali (qs), permanenti (qp) e accidentali (qa) è possibile ricavare il carico totale permanente (G) e il carico totale accidentale (Q)

G=(q_s + q_p) * A_tot

Q=q_a * A_tot

Dunque calcoliamo il peso sismico W introducendo un coefficiente di contemporaneità ψ_2j(che in ambienti residenziali è pari a 0.3).

W= G + ψ_{2j *} Q

Introducendo un coefficiene di intensità sismica c(a Roma pari a 0,10) è possibile calcolare la forza che applicheremo al centro delle masse

F= W *c

STEP6

Oltre il calcolo della traslazione orizzontale u

u=F/ k_otot

viene calcolato il momento generato dalla forza sismica

M=F* (YG-YC)

Dunque, conoscendo anche k_φ,  si ricava la rotazione φ

Φ = M/ k_φ

Quindi è possibile capire come si ripartisce la forza sismica lungo x sui controventi.

La reazione elastica di quelli orizzontali sarà il prodotto della rigidezza traslante per la somma degli spostamenti (traslazione orizzontale e rotazione per braccio).

F_{o_n}= k_{o_n} *(u + φ*dd _{o_n})

La reazione elastica di quelli verticali sarà il prodotto della rigidezza traslante per lo spostamento (rotazione per braccio).

F_{v_n}= k_{v_n} * φ*dd _{v_n}

STEP7

Oltre il calcolo della traslazione verticale v

v=F/ k_vtot

viene calcolato il momento generato dalla forza sismica

M=F* (XG-XC)

Dunque, conoscendo anche k_φ,  si ricava la rotazione φ

Φ = M/ k_φ

Quindi è possibile capire come si ripartisce la forza sismica lungo y sui controventi.

La reazione elastica di quelli orizzontali sarà il prodotto della rigidezza traslante per lo spostamento (rotazione per braccio).

F_{o_n}= k_{o_n} *φ*dd _{o_n})

La reazione elastica di quelli verticali sarà il prodotto della rigidezza traslante per la somma degli spostamenti (traslazione verticale e rotazione per braccio).

F_{v_n}= k_{v_n} * (v + φ*dd _{v_n})

 

 

 

Questa esercitazione consiste nel dimensionamento del pilastro più sollecitato in un telaio nelle tre diverse tecnologie: legno, acciaio e cemento armato.

L1 = 7m

L2 = 5m

Area di influenza = L1 x L2 = 35m²

Numero piani = 4

 

Il pilastro sottoposto a maggiore sforzo normale nella struttura presa in analisi è quello evidenziato in rosso: su di esso infatti grava il carico di travi e solaio per la maggiore area di influenza che dovrà essere moltiplicato per il numero dei piani sovrastanti.

LEGNO

 

Contributo delle travi

Si calcola moltiplicando il peso unitario di ciascuna trave (considero il peso unitario della trave calcolato nella prima esercitazione) per l’interasse, moltiplicando il valore ottenuto per il coefficiente di sicurezza per carichi strutturali pari a 1.3.

 

Qtravi = (Peso unitario trave1 x  L1 x 1.3) + (Peso unitario trave2 x L2 x 1.3)

 

Contributo del solaio

Si ottiene moltiplicando la somma dei carichi (strutturali, permanenti e accidentali calcolati nella prima esercitazione e maggiorati dei rispettivi coefficienti di sicurezza) per l’area di influenza.

 

Qsolaio = [(qs x1.3) + (qp x 1.5) + (qa x 1.5)] x area di influenza

 

È dunque possibile calcolare lo sforzo normale agente sul pilastro del piano terra

N = (Qtravi + Qsolaio) x 4 piani

 

Un pilastro sottoposto a compressione può essere soggetto a rottura per schiacciamento del materiale o soggetto all’innesco del fenomeno di instabilità.

 

Per evitare il fenomeno di rottura per schiacciamento la tensione massima nel pilastro (σmax) deve essere minore della resistenza a compressione di progetto del materiale (fcd).

 

σmax < fcd

 

Imponendo σmax = fcd possiamo ricavare l’area minima della sezione ovvero il valore minimo che deve avere l’area per non essere soggetta a rottura.

Infatti poiché

σmax = N/Amin

fcd = N/Amin

 

In fase progettuale si è scelto per il pilastro un legno lamellare GL24h con resistenza caratteristica fmk pari a 24 Mpa. La resistenza di progetto fd che viene calcolata dal foglio tiene conto della resistenza caratteristica corretta con alcuni parametri:

fd = (kmod x fmk)/γm

γm è un coefficiente di sicurezza del materiale: in questo caso per il legno lamellare γm = 1.45.

Kmod è un coefficiente correttivo che tiene conto della durata di carico (consideriamo una durata media) e dell’umidità della struttura (consideriamo una classe media).

 

dunque ora, conoscendo il valore di fcd, è possibile calcolare l’area minima con la formula inversa.

Amin =N/fcd

 

Affinché, invece, nel pilastro non si inneschi un fenomeno di instabilità lo sforzo nomale deve essere inferiore allo sforzo critico euleriano.

 

N<Ncrit

 

Sappiamo che

Ncrit= (π²EImin)/(βl)²

 

Poiché

βl = l0 (lunghezza libera di inflessione)

Imin=Aρmin²

 

Ncrit = (π²EAρmin²)/(l0)²

 

Poiché λ=l0/ρmin

Ncrit = π²EA/ λ²

 

Allo sforzo critico euleriano è possibile associale una tensione critica

σcrit = Ncrit/A = π²E/ λ²

 

Per evitare il fenomeno di instabilità la tensione massima nel pilastro (σmax) deve essere minore della tensione critica (σcrit)

σmax < σcrit

 

Poiché abbiamo imposto

σmax = fcd

allora

 

fcd < σcrit    (prima di inflettersi per instabilità, il pilastro si rompe. Questa soluzione è

                       ottimale poiché l’instabilità non è controllabile)

fcd < π²E/ λ²

λ² < π²E/fcd

λmax = π √(E/fcd)

Dunque una volta inseriti i valori del modulo di elasticità (E) proprio del materiale e la resistenza di progetto (fcd), il foglio di calcolo ricava la snellezza massima del pilastro (λmax).

Ma, poiché

λ = l0/ρmin

 

ρmin = l0/λ

 

Dunque una vola inseriti i valori di β e della lunghezza del pilastro (l), si ottiene il valore della lunghezza libera di inflessione (l0) che il foglio di calcolo dividerà per la snellezza massima appena ricavata: dunque si ottiene il raggio di inerzia minimo. Ricordando che nelle sezioni rettangolari

ρmin = √(1/12) b

possiamo ricavare la base tramite la formula inversa:

bmin = 2√3 ρmin

Una volta ingegnerizzata calcoliamo l’altezza minima

hmin= Amin/b

Una volta ingegnerizzata anche l’altezza il foglio ricalcola l’area e il momento d’inerzia di design. Dunque sarà necessario verificare che l’area di design sia maggiore dell’area minima precedentemente calcolata.

 

ACCIAIO

Per calcolare lo sforzo normale agente sul pilastro si sommano nuovamente i contributi di travi e solaio all’interno dell’area di influenza e si moltiplicano per il numero di piani.

Anche in questo caso, per ricavare il contributo delle travi, si sceglie il peso unitario delle travi della prima esercitazione e si moltiplica per l’interasse relativo e per il coefficiente si sicurezza strutturale.

Qtravi = (Peso unitario trave1 x  L1 x 1.3) + (Peso unitario trave2 x L2 x 1.3)

 

Poi per ricavare il contributo del solaio si scelgono i valori dei carichi strutturali, permanenti e accidentali della prima esercitazione, si maggiorano con i relativi coefficienti di sicurezza e la loro somma viene moltiplicata per l’area di influenza.

Qsolaio = [(qs x1.3) + (qp x 1.5) + (qa x 1.5)] x area di influenza

 

È dunque ora possibile calcolare lo sforzo normale agente sul pilastro del piano terra

N = (Qtravi + Qsolaio) x 4 piani

 

Avendo scelto per la trave un acciaio S275 con resistenza caratteristica fyk=275Mpa, si ricava la resistenza di progetto correggendo quella caratteristica con un coefficiente di sicurezza γm=1.05.

fyd = fyk/γm

Dunque imponendo σmax = fyd possiamo ricavare l’area minima della sezione come sopra:

 

Amin= N/fyd

 

Come per il legno inserendo i dati relativi al modulo di elasticità (E) relativo al materiale e la resistenza di progetto (fyd) appena calcolata, il foglio ricava il valore della snellezza massima

λmax = π √(E/fcd)

Inserendo poi i valori di β e della lunghezza del pilastro (l), si ottiene il valore della lunghezza libera di inflessione (l0) che il foglio di calcolo dividerà per la snellezza massima appena ricavata: dunque si ottiene il raggio di inerzia minimo.

ρmin = l0/λ

 

Ora, poiché la sezione di un pilastro in acciaio non è rettangolare, bensì sarà un profilo HEA possiamo calcolare il momento di inerzia minimo con la formula

Imin = A x ρmin²

Ora sarà possibile scegliere su un sagomario l’HEA che possiederà un momento inerzia, un raggio di inerzia e un area immediatamente superiori a quelle trovate. Il foglio ricalcolerà la snellezza con i nuovi valori e si dovrà verificare che non superi il valore 200.

 

CEMENTO ARMATO

Per calcolare lo sforzo normale agente sul pilastro si sommano nuovamente i contributi di travi e solaio all’interno dell’area di influenza e si moltiplicano per il numero di piani.

Anche in questo caso, per ricavare il contributo delle travi, si sceglie il peso unitario delle travi della prima esercitazione e si moltiplica per l’interasse relativo e per il coefficiente si sicurezza strutturale.

Qtravi = (Peso unitario trave1 x  L1 x 1.3) + (Peso unitario trave2 x L2 x 1.3)

 

Poi per ricavare il contributo del solaio si scelgono i valori dei carichi strutturali, permanenti e accidentali della prima esercitazione, si maggiorano con i relativi coefficienti di sicurezza e la loro somma viene moltiplicata per l’area di influenza.

Qsolaio = [(qs x1.3) + (qp x 1.5) + (qa x 1.5)] x area di influenza

 

È dunque ora possibile calcolare lo sforzo normale agente sul pilastro del piano terra

N = (Qtravi + Qsolaio) x 4 piani

 

Scelgo poi un calcestruzzo classe C60/75 con resistenza caratteristica fck = 60 Mpa.

Il foglio di calcolo ricava la resistenza di progetto con la formula

Fcd= (α x fck)/ γm

Dove γm è il coefficiente di sicurezza di 1.5

e α è un coefficiente che tiene conto del tempo pari a 0.85

 

Dunque imponendo σmax = fcd possiamo ricavare l’area minima della sezione come sopra:

 

Amin= N/fcd

 

Come per il caso di legno e acciaio inserendo i dati relativi al modulo di elasticità (E) relativo al materiale e la resistenza di progetto (fyd) appena calcolata, il foglio ricava il valore della snellezza massima

λmax = π √(E/fcd)

Inserendo poi i valori di β e della lunghezza del pilastro (l), si ottiene il valore della lunghezza libera di inflessione (l0) che il foglio di calcolo dividerà per la snellezza massima appena ricavata: dunque si ottiene il raggio di inerzia minimo.

ρmin = l0/λ

 

Come nel caso del legno possiamo ricavare la base tramite la formula:

bmin = 2√3 ρmin

Una volta ingegnerizzata calcoliamo l’altezza minima

hmin= Amin/b

Una volta ingegnerizzata anche l’altezza, il foglio ricalcola l’area e il momento d’inerzia di design.

 

Per il pilastro in calcestruzzo è necessario aggiungere un ulteriore verifica. Infatti il pilastro non sarà soggetto a sola compressione, ma anche a flessione derivante dall’incastro che avremo nel nodo trave pilastro. Dunque per verificare a presso-flessione dovremo controllare che la tensione massima dovuta sia allo sforzo normale che al momento flettente sia inferiore alla tensione di progetto.

σmax = N/A + Mt/Wmax < fcd

Dunque il foglio, avendo tutti i dati, calcola automaticamente il modulo di resistenza a flessione Wmax

Wmax= bh²/6

E il momento all’estremo della trave e quindi sulla testa del pilastro che viene calcolato come

Mt= (qt x Lp²)/12

Dove qt (calcolato da foglio) è il carico di solaio distribuito sulla trave principale: quindi si sommano i carichi strutturali, permanenti e accidentali maggiorati per l’interasse tra le travi principali ovvero qt = [(qs x 1.3) + (qp x 1.5) + (qa x 1.5)] x Ls.

Dunque il foglio di calcolo ricava il σmax e verifica se risulta minore di fcd. Se non risulta verificato sarà necessario aumentare gradualmente le dimensioni del pilastro fino alla verifica di questa condizione.

 

 

Questa terza esercitazione consiste nel verifica della deformazione della mensola più sollecitata di un telaio in tre differenti tipologie: legno, acciaio e cemento armato.

La mensola sottoposta a maggiore carico nella struttura presa in analisi è quella evidenziata in rosso: su di essa infatti grava il carico di solaio maggiore.

Luce: 3m

Interasse: 6m

Area di influenza: 18m²

 

 

LEGNO

Prima di calcolare e verificare la deformazione di una mensola è necessario dimensionare l’altezza della stessa. Consideriamo lo stesso pacchetto di solaio della prima esercitazione e, come nel caso della trave inflessa, inseriamo nel foglio i dati inerenti all’interasse, al carico strutturale, permanente e accidentale. In questo modo otteniamo il carico ultimo. qu = [(qs x 1.3) + (qp x 1.5) + (qa x 1.5)] x i

 

Inserendo la luce il foglio ricava il momento massimo: nel caso della mensola pari a Mmax= (qu x L²)/2

Una volta inserita la resistenza caratteristica (nel caso del legno lamellare GL24h pari a 24 Mpa), il coefficiente di sicurezza del materiale (per il legno lamellare γm=1.45) e il coefficiente correttivo per umidità e durata del carico (consideriamo una classe media con kmod=0.8) il foglio ricava la resistenza di progetto

 

fd = (kmod x fmk)/γm.

 

Impostando la base della trave, si determina l’altezza minima come nel caso della trave inflessa. Scegliamo dunque un’altezza ingegnerizzata.

 

Ora possiamo procedere al calcolo e alla verifica della deformazione.  Con i dati già presenti del foglio si ricava il momento di inerzia che, nel caso di una sezione rettangolare, è Ix= bh³/12. Possiamo anche calcolare il carico di esercizio pari alla somma dei carichi maggiorati con i relativi coefficienti di sicurezza (1 nel caso dei carichi strutturali e permanenti, 0.5 nel caso dei carichi accidentali) per l’interasse.

qe= [(qs x 1) + (qp x 1) + (qa x 1.5)] x i

 

Nel caso di una semplice mensola con carico uniformemente distribuito sappiamo che:

v(s) = 1/(EI) x [- (ql²s²)/4 – (qs⁴)/24 + (qls³)/6]

Poiché il massimo spostamento in una mensola avviene nell’estremo libero (cioè s=l) possiamo anche scrivere che

vmax= - (ql⁴)/8EI.

In realtà questo valore di spostamento massimo è un approssimazione: infatti esso viene associato ad una vera mensola mentre, in questo caso, la struttura si configura come aggetto di una trave appoggiata. Poiché la luce della trave appoggiata è 8m e l’aggetto è 3m (<8m/2) il vmax calcolato è maggiorato.

 

Dunque inserendo il modulo di elasticità E proprio del materiale nella tabella possiamo ricavare questo valore considerando come carico quello di esercizio (qe).

 

Affinchè la mensola sia verificata vmax < (1/250) x l. Dunque devo verificare che:

l/vmax >250.

In questo caso 439.70 > 250 dunque la mensola in legno è verificata!

 

ACCIAIO

 

Come nel caso del legno dobbiamo innanzitutto dimensionare l’altezza della mensola.  Inseriamo i dati inerenti l’interasse, la luce e i carichi del pacchetto di solaio considerato nella prima esercitazione. Il foglio di calcolo ricava carico ultimo e momento massimo della mensola come sopra. Inserendo la resistenza caratteristica del materiale (fyk=275Mpa per un acciaio S275) si ottiene la resistenza di progetto fd moltiplicando fyk per il coefficiente di sicurezza γm=1.05. Come nel caso della trave appoggiata imponendo σmax = fd e utilizzando la formula di Navier sappiamo che

 

Wxmin = Mx/fd

 

Dunque scegliamo nel sagomario una trave IPE con modulo di resistenza a flessione W immediatamente superiore. In questo caso un IPE 400. Dunque riportiamo sulla tabella i relativi valori di momento d’inerzia Ix e di peso della trave IPE 400 e il modulo di elasticità E proprio del materiale.

 

A differenza del legno il foglio calcola il carico di esercizio sommando ai carichi maggiorati e moltiplicati per l’interasse anche il peso della trave (nel caso del legno il peso della trave viene trascurato trattandosi di un materiale leggero). Dunque

qe= [(qs x 1) + (qp x 1) + (qa x 1.5)] x i + (peso trave x 1)

 

Con la stessa formula precedentemente utilizzata per il legno ricaviamo lo spostamento massimo: vmax= - (ql⁴)/8EI     (anche in questo caso maggiorato).

 

Anche in questo caso il rapporto l/vmax = 440.082 > 250 dunque la mensola in acciaio è verificata!

 

CEMENTO ARMATO

 

Anche per il cemento armato dobbiamo prima calcolare l’altezza della mensola. Inserendo interasse, luce e carichi del pacchetto di solaio in latero-cemento della prima esercitazione otteniamo carico ultimo e momento massimo. Una volta scelto il tipo di barre (B450C con resistenza caratteristica fyk= 450Mpa) e la classe del calcestruzzo (C60/75 con resistenza caratteristica fck = 60 Mpa) il foglio ricava le corrispettive resistenze di progetto corrette con i coefficienti di sicurezza.

 

Una volta impostata la dimensione della base della trave il foglio ricava l’altezza utile come nel caso della trave appoggiata. Questo valore sommato per il copriferro permette di ricavare un’altezza minima che possiamo ingegnerizzare. Il foglio ricava direttamente l’area (base per altezza) e il peso al metro quadro (area per peso specifico del cls).

 

Nella riga sottostante il foglio ricalcola il valore del carico ultimo aggiungendo a quello precedente il peso della trave moltiplicato per il coefficiente per carichi strutturali pari a 1.3. Viene ricalcolato dunque il momento massimo e, mantenendo i valori delle resistenze e delle dimensioni scelte nel progetto, ricalcola l’altezza minima. Anche con il peso della trave l’altezza minima rimane inferiore al valore di altezza ingegnerizzata che avevamo scelto dunque l’altezza è verificata.

 

Ora possiamo procedere con il calcolo e la verifica dello spostamento massimo della mensola. Come nel caso dell’acciaio il foglio calcola il carico di esercizio sommando ai carichi maggiorati e moltiplicati per l’interasse anche il peso della trave.

qe= [(qs x 1) + (qp x 1) + (qa x 1.5)] x i + (peso trave x 1)

 

Inserendo il valore del modulo di elasticità E proprio del materiale e calcolando il momento d’inerzia Ix per una sezione rettangolare (come nel caso del legno Ix= bh³/12) il foglio ricava lo spostamento massimo

vmax= - (ql⁴)/8EI    (anche in questo caso maggirato)

 

Anche in questo caso il rapporto l/vmax = 286.21> 250 dunque la mensola in cemento armato è verificata!

 

 

 

 

 

 

 

 

Questa seconda esercitazione si basa sul dimensionamento di una travatura reticolare tridimensionale. Attraverso il software SAP2000 è possibile disegnare la struttura e vincolarla esternamente tramite quattro appoggi.

Trattandosi di una struttura reticolare possiamo modellizzare i nodi come delle cerniere interne.

 

Una volta scelto il materiale (acciaio) e i profili delle sezioni (circolari cavi) sono state applicate forze concentrate sui nodi superiori della travatura.

 

 Il software permette di visualizzare la struttura deformata e i grafici relativi allo sforzo normale: in rosso le aste compresse (puntoni), in blu le aste tese (tiranti).

 

 

 È possibile poi esportare i valori numerici degli sforzi assiali delle singole aste in una foglio di calcolo.

Innanzitutto il file va pulito mantenendo solo i valori di station pari alla lunghezza effettiva dell’asta. Dunque nel caso di questa struttura è necessario mantenere le aste di 2m che corrispondono ai lati del quadrato di base (nere); le aste lunghe 2.82m che corrispondono alle diagonali dei quadrati di base (verde); le aste lunghe 2.44m che corrispondo ai lati della piramide (arancio).

Quindi è possibile ordinare la tabella in funzione dello sforzo normale dal valore maggiore al valore minore e quindi si possono individuare facilmente le aste più tese nella struttura (valori maggiori con segno positivo) e quali quelle più compresse (valori maggiori con segno negativo).

 

TRAZIONE

Un ulteriore foglio di calcolo ci permetterà di dimensionare i profili circolari cavi per le aste tese.

Infatti, una volta inseriti i valori degli sforzi normali e scelto il tipo di acciaio (un acciaio S235 con resistenza caratteristica fyk = 235 Mpa), il foglio calcolerà la resistenza di progetto fd correggendo quella caratteristica con un coefficiente di sicurezza γm=1.05 e l’area minima dividendo lo sforzo normale per la resistenza di progetto appena calcolata

Amin = N/fd

Infatti abbiamo imposto che σ=fd.

Consultando la tabella dei profilati circolari cavi dovremmo scegliamo il profilo con area immediatamente maggiore per ciascuna asta, ma ciò comporterebbe un eccessivo costo e difficoltà di montaggio nella realizzazione della reticolare. Dunque si scelgono 4 profili che soddisfino le aree minime delle aste tese. Si aggiungono dunque due nuove colonne con il tipo di profilo scelto e il numero di asta corrispondente.

COMPRESSIONE

Un ulteriore foglio di calcolo ci permetterà di dimensionare i profili circolari cavi per le aste compresse.

Come nel caso della trazione, una volta inserito lo sforzo normale e il tipo di acciaio, è possibile ricavare la resistenza di progetto e dunque l’area minima imponendo nuovamente σ=fd.

Amin = N/fd

Nel caso della compressione, però, dobbiamo considerare anche l’instabilità euleriana. Dunque sarà necessario imporre σcrit = fd.

fd = σcrit = Ncrit/A = (π²E)/λ²

dunque λ = π/√(E/fyd)

Dove E è il modulo di elasticità dell’acciaio pari a 210000Mpa. Nella tabella possiamo aggiungere due ulteriori valori noti: β = 1 (trattandosi di un asta incernierata) e le luci delle aste. Con questi nuovi dati possiamo calcolare ρmin.

ρmin = L0/ λ

dove L0= β x l

Ora sapendo che ρmin²=Imin/A

Imin = ρmin²/A

Consultando la tabella dei profilati circolari cavi dovremmo scegliere il profilo con area e momento di inerzia immediatamente maggiori per ogni asta. Come per quelle tese sarà necessario scegliere un numero di profili limitati per semplificare il montaggio e ammortizzare i costi: sono stati scelti dunque 4 profili che soddisfino le aree e le inerzie minime delle aste compresse controllando che la snellezza λ sia inferiore di 200. Si aggiungono dunque due nuove colonne con il tipo di profilo scelto e il numero di asta corrispondente.

 

 

 

 

 

 

 

 

Questa prima esercitazione consiste nel dimensionamento della trave più sollecitata di un telaio in tre differenti tipologie: legno, acciaio e cemento armato.

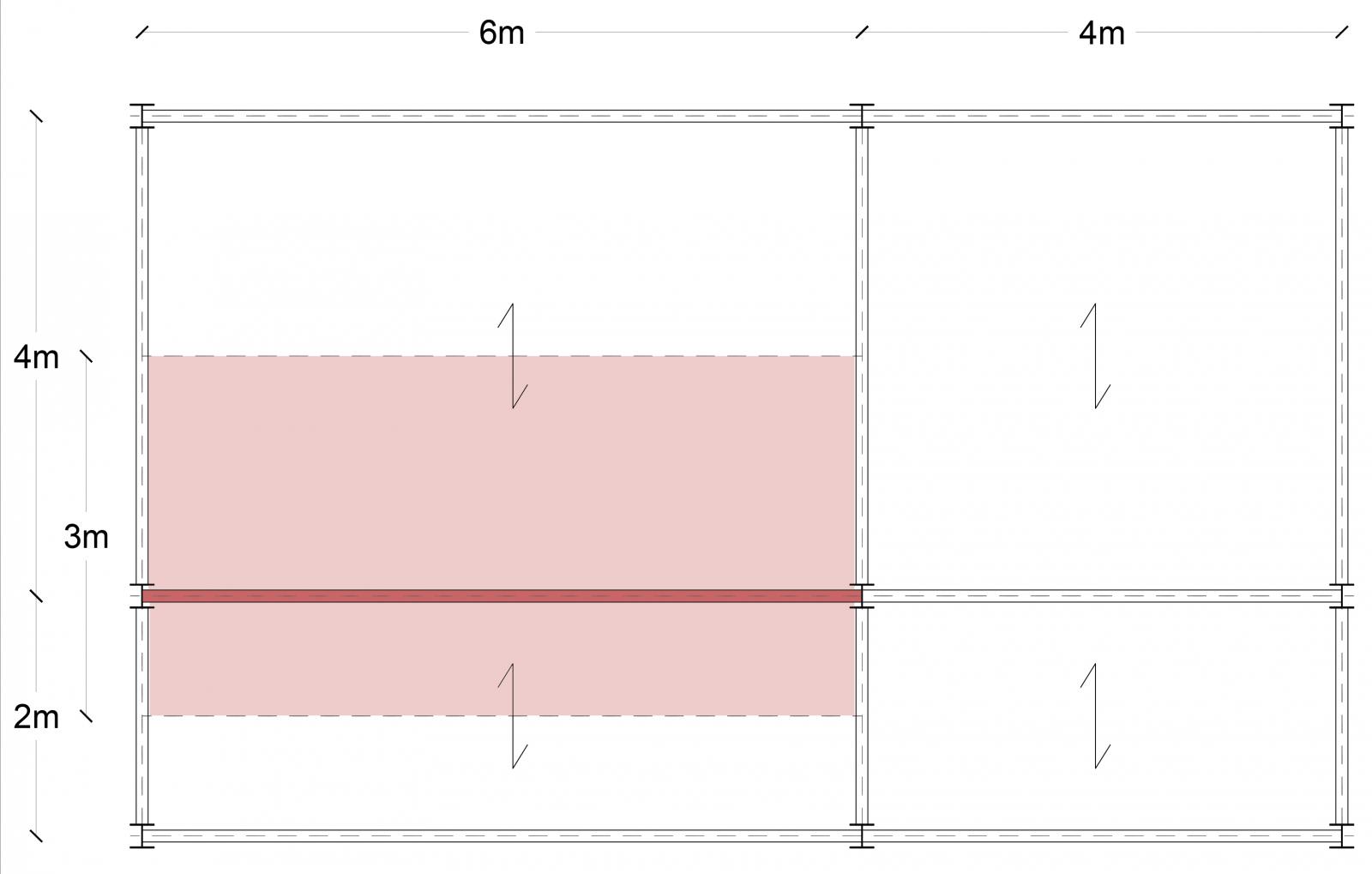
La trave sottoposta a maggiore carico nella struttura presa in analisi è quella evidenziata in rosso: su di essa infatti grava il carico di solaio maggiore.

Luce:6m                                                                                                                                                    Interasse:3m                                                                                                                                                   Area di influenza: 18m²

LEGNO

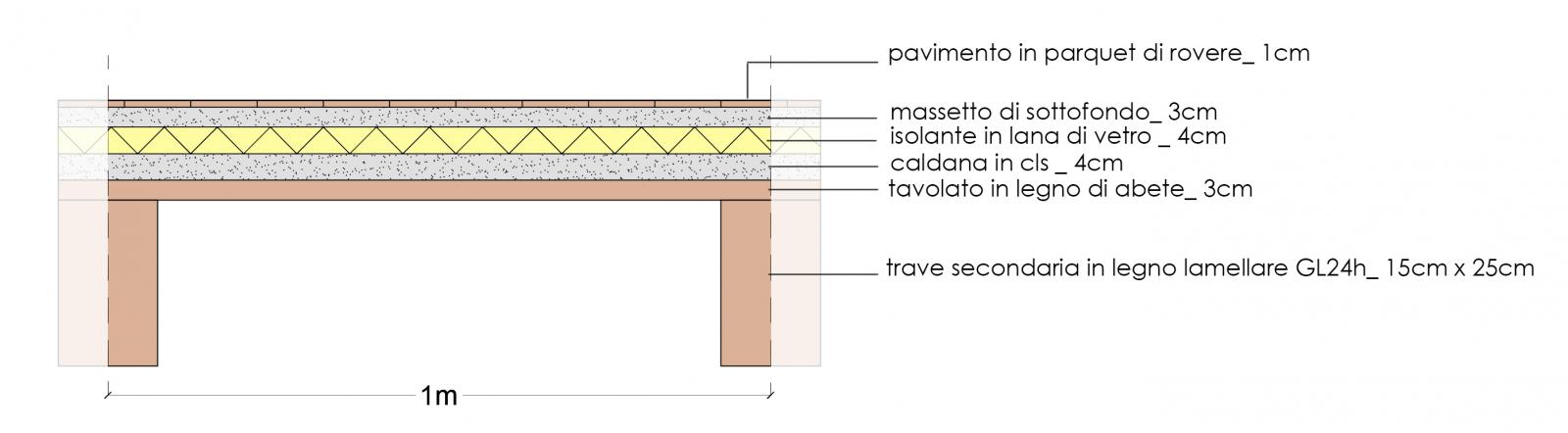
Conoscendo la stratigrafia del solaio (dunque spessori e pesi specifici dei vari componenti) possiamo ricavare il volume e il peso al metro quadro di ciascun componente. Quindi è possibile calcolare i differenti tipi di carico: strutturale, permanente e accidentale.

 

Il carico strutturale (qs) si ottiene sommando i contributi di peso dei travetti e del tavolato.

 

Travetto in legno lamellare GL24h                                                                          

Sezione: 15cm X25cm                                                                                                

Peso Specifico: 380 kg/m³ = 3.8 kN/m³                                                            

Volume: 0.15m x 0.25m x 1m = 0. 0375 m³                                                                

Peso al metro quadro: 0.0375 m³/m² x 3.8 kN/m³ = 0.143kN/m²

 

Tavolato in legno di abete                                                                                            

Spessore: 3 cm                                                                                                          

Peso Specifico: 450 Kg/m³ =4.5 kN/m³                                                                        

Volume: 0.03m x 1m x 1m = 0.03 m³                                                                          

Peso al metro quadro: 0.03 m³/m² x 4.5 kN/m³ = 0.135 kN/m²

 

qs = (0.143 + 0.135) kN/m² = 0.28 kN/m²

 

Il carico permanente (qp) si ottiene sommando i contributi della caldana, dell’isolante, del massetto e del pavimento. A questo carico si somma anche il carico dovuto a tramezzi (1 KN/m²) e impianti (0.5 KN/m²).

 

Pavimento in parquet di rovere                                                                                 

Spessore: 1 cm                                                                                                          

Peso Specifico: 720 kg/m³ = 7.20kN/m³                                                                      

Volume: 0.01m x 1m x 1m = 0.01 m³                                                                          

Peso al metro quadro: 0.01 m³/m² x 7.20 kN/m³ = 0.072 kN/m²

 

Massetto di sottofondo                                                                                                

Spessore: 3 cm                                                                                                          

Peso Specifico: 1800 kg/m³ = 18kN/m³                                                                        

Volume: 0.03m x 1m x 1m = 0.03 m³                                                                          

Peso al metro quadro: 0.03 m³/m² x 18 kN/m³ = 0.54 kN/m²

 

Isolante in lana di vetro                                                                                              

Spessore: 4 cm                                                                                                          

Peso Specifico: 20 kg/m³ = 0.2 kN/m³                                                                         

Volume: 0.04m x 1m x 1m = 0.04 m³                                                                          

Peso al metro quadro: 0.04 m³/m² x 0.2 kN/m³ = 0.008 kN/m²

 

Caldana in cls con rete elettrosaldata                                                                            

Spessore: 4 cm                                                                                                           

Peso Specifico: 2400 Kg/m³ = 24 kN/m³                                                                       

Volume: 0.04m x 1m x 1m = 0.04 m³                                                                           

Peso al metro quadro: 0.04 m³/m² x 24 kN/m³ = 0.96 kN/m²

 

qp = (0.072 + 0.54 + 0.008 + 0.96) kN/m² + 1.5 kN/m²  = 3.08 kN/m²

 

Il carico accidentale (qa) dipende dalla destinazione d’uso dell’edificio: in questo caso consideriamo un ambiente ad uso residenziale, dunque 2 kN/m².

qa = 2 kN/m²

 

Inserendo il valore dell’interasse e dei vari carichi, il foglio di calcolo ricava il carico ultimo, ovvero il carico dell’area di influenza del solaio distribuito su tutta la lunghezza della trave sollecitata. Il carico ultimo si ottiene moltiplicando la somma dei carichi maggioranti con le rispettive costanti di sicurezza (1,3 per il carico strutturale e 1,5 per il carico permanente e accidentale) per l’interasse.                                                                        

qu = [(qs x 1.3) + (qp x 1.5) + (qa x 1.5)] x i

Inserendo la luce il foglio di calcolo permette di ricavare il valore del momento massimo di una trave appoggiata:

Mmax = (qu x L²)/8

In fase progettuale si è scelto per la trave un legno lamellare GL24h con resistenza caratteristica fmk pari a 24 Mpa. La resistenza di progetto fd, che viene calcolata dal foglio, tiene conto della resistenza caratteristica corretta con alcuni parametri:

fd = (kmod x fmk)/γm

γm è un coefficiente di sicurezza del materiale: in questo caso per il legno lamellare γm = 1.45. Kmod è un coefficiente correttivo che tiene conto della durata di carico (consideriamo una durata media) e dell’umidità della struttura (consideriamo una classe media).

Impostando la base della trave, il foglio di calcolo determina l’altezza minima di 49,42cm.

Infatti imponendo σmax = fd

Wx = Mx/fd                                                            dalla formula di Navier             

Wx = Ix/ymax = ((bh³)/12)/(h/2) = (bh²)/6            Wx in una sezione rettangolare

Quindi mettendo a sistema

(bh²)/6 =Mx/fd

h=√(6Mx/ (fd x b))

Scelgo dunque una trave con base 20 cm e altezza ingegnerizzata H=50 cm.

 

Per effettuare una verifica sommo al carico ultimo (qu) nel foglio di calcolo il peso della trave (maggiorato al coefficiente di sicurezza per carichi strutturali)

Peso della trave: (0.2m x 0.50m x 1m) / m x 3.8 kN/m³ = 0.38 kN/m

 

L’altezza minima della trave diventa 49.92 cm, rimanendo dunque inferiore a 50cm.

La sezione 20cm x 50cm è dunque verificata.

 

 

ACCIAIO

Consideriamo ora lo stesso solaio in acciaio.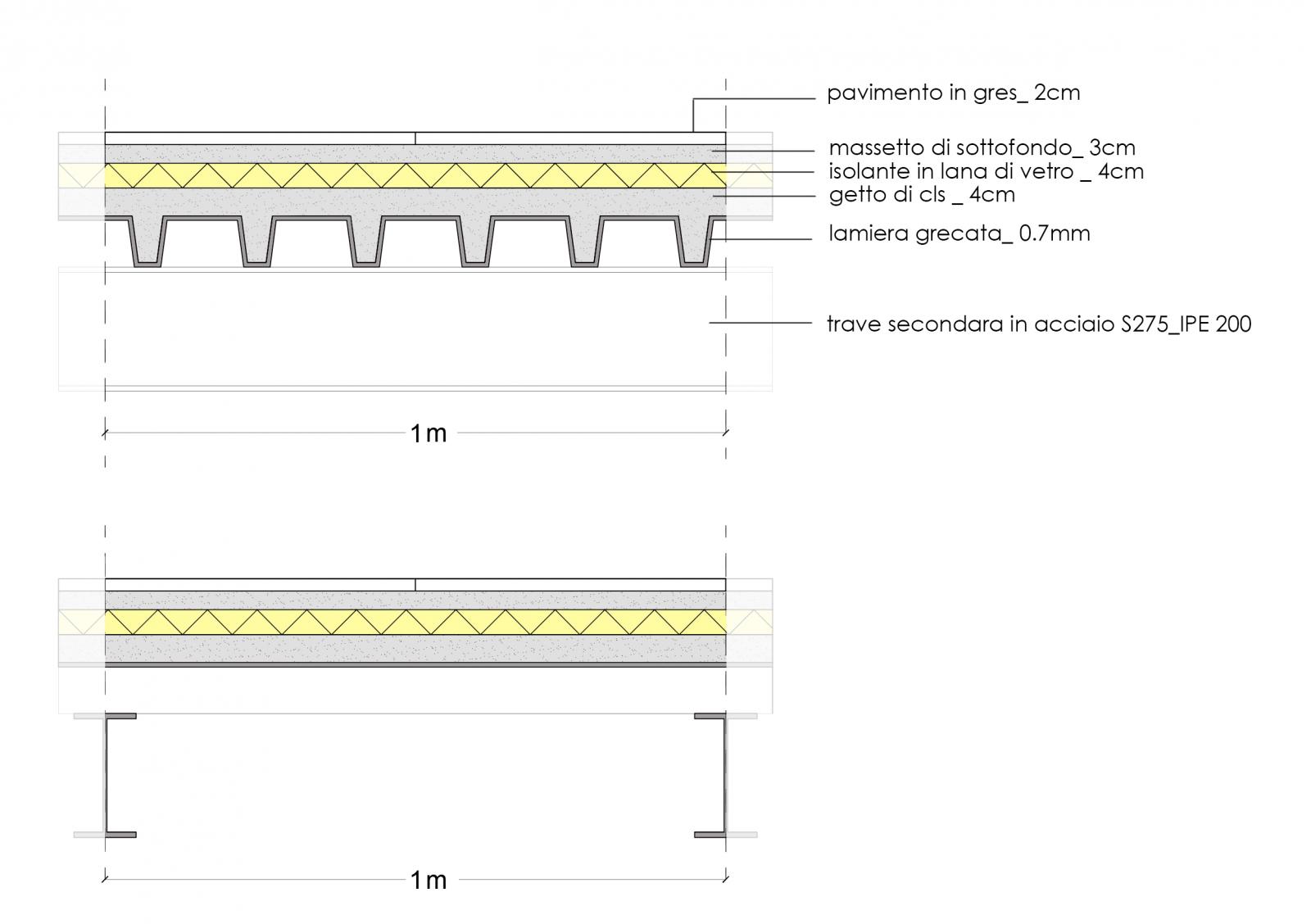

 

Il carico strutturale (qs) dipende dal peso delle travi secondarie, della lamiera grecata e della soletta in cls.

 

Travetto IPE 200 di acciaio S275                                                                                            

Area: 28.5 cm² = 0.00285m²                                                                                       

Peso: 22.4 kg/m = 0.224 kN/m                                                                                    

Peso al metro quadro: 0.224 kN/m²

 

Lamiera grecata                                                                                                          

Spessore: 0.7mm                                                                                                        

Peso al metro quadro: 9.64 kg/m² = 0.0964 kN/m²

 

Getto di cls                                                                                                                  

Sezione: 0.063 m²                                                                                                        

Peso Specifico: 2400 kg/m³ =24 kN/m³                                                                         

Volume: 0.063 m² x 1m = 0.063 m³                                                                              

Peso al metro quadro: 0.063 m³/m² x 24 kN/m³ = 1.512 kN/m²

 

Qs = (0.224 + 0.0964 + 1.512) kN/m² = 1.83 kN/m²

 

Il carico permanente (qp) dipende dal peso dell’isolante, del massetto e del pavimento aggiungendo il contributo di tramezzi e impianti.

 

Isolante in lana di vetro                                                                                                

Spessore: 4cm                                                                                                             

Peso specifico: 20 kg/m³ = 0.2kN/m³                                                                            

Volume: 0.04m x 1m x 1m = 0.04 m³                                                                            

Peso al metro quadro: 0.04 m³/m² x 0.2 kN/m³ = 0.008 kN/m²

 

Massetto di sottofondo                                                                                                  

Spessore: 3cm                                                                                                             

Peso specifico: 2000kg/m³ = 20kN/m³                                                                           

Volume: 0.03m x 1m x 1m = 0.03 m³                                                                            

Peso al metro quadro: 0.03 m³/m² x 20 kN/m³ = 0.6 kN/m²

 

Pavimento gres porcellanato                                                                                          

Spessore: 2cm                                                                                                             

Peso al metro quadro: 40 kg/m² = 0.4 kN/m²

 

Qp = (0.008 + 0.6 + 0.4) kN/m² + 1.5 kN/m² = 2.51 kN/m²

 

Il carico accidentale (qa) rimane legato all’ambiente residenziale:

Qa = 2 kN/m²

 

Inserendo il valore dell’interasse e dei carichi il foglio calcola il carico ultimo come sopra. Poi inserendo la luce il foglio calcola il momento massimo nella trave appoggiata.

Avendo scelto per la trave un acciaio S275 con resistenza caratteristica fyk=275Mpa, si ricava la resistenza di progetto correggendo quella caratteristica con un coefficiente di sicurezza γm=1.05.

Essendo in fase progettuale imponiamo

σmax = fd

Dunque dalla formula di Navier:

Wxmin = Mx/fd.

Quindi scegliamo il Wx immediatamente superiore a quello appena calcolato nel sagomario delle travi IPE a cui corrisponde una trave IPE300.

 

Ora sommiamo il peso della trave (0.422 kN/m) al carico ultimo maggiorato dell’opportuno coefficiente di sicurezza.

 

Wxmin rimane comunque inferiore al Wx scelto, dunque la sezione IPE 300 è verificata.

 

 

CEMENTO ARMATO

Consideriamo ora lo stesso solaio in cemento armato.

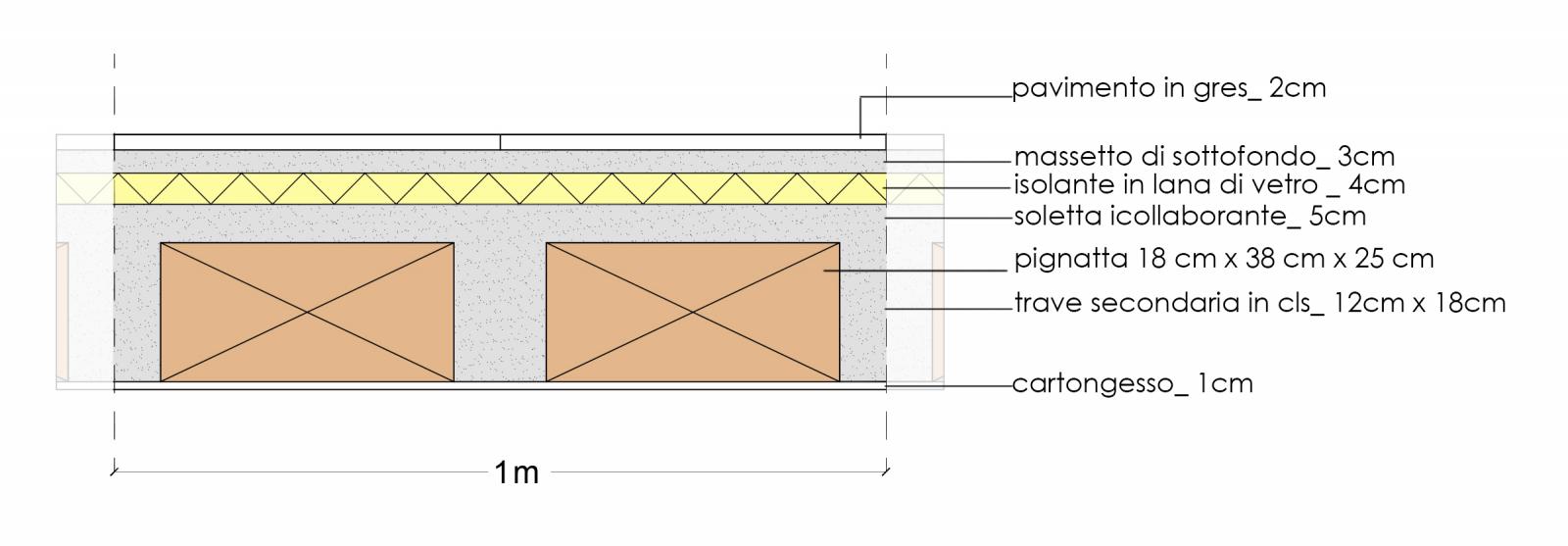
Il carico strutturale (qs) dipende dal peso dei travetti, della soletta in cls e delle pignatte.

 

Travetti in cls                                                                                                               

Dimensioni: 12cm x 18cm                                                                                             

Peso Specifico: 2400 kg/m³ = 24kN/m³                                                                         

Volume: 2 x 0.12m x 0.18m x 1m = 0.043 m³                                                                

Peso al metro quadro: 0.043 m³/m² x 24 kN/m³ = 1.04 kN/m²

 

Soletta collaborante in cls                                                                                             

Spessore: 5cm                                                                                                             

Peso Specifico: 2400 kg/m³ = 24kN/m³                                                                         

Volume: 0.05m x 1m x 1m = 0.05 m³                                                                            

Peso al metro quadro: 0.05 m³/m² x 24 kN/m³ = 1.2 kN/m²

 

Pignatte                                                                                                                       

Dimensioni: 18cm x 38cm x 25cm                                                                                 

Peso: 7.90 Kg/cad                                                                                                        

Peso al metro quadro: 63.2 Kg/m² = 0.63kN/m²

 

Qs= (1.04 + 1.2 + 0.63) kN/m² = 2.87 kN/m²

 

Il carico permanente (qp) dipende dal peso del pavimento, del massetto, dell'isolante e del rivestimento aggiungendo il contributo di tramezzi e impianti.

 

Pavimento in gres                                                                                                        

Spessore: 2cm                                                                                                             

Peso al metro quadro: 40 kg/m² = 0.4 kN/m²

 

Massetto di sottofondo                                                                                                  

Spessore: 3cm                                                                                                              

Peso specifico: 2000kg/m³ = 20kN/m³                                                                           

Volume: 0.03m x 1m x 1m = 0.03 m³                                                                             

Peso al metro quadro: 0.03 m³/m² x 18 kN/m³ = 0.54 kN/m²

 

Isolante in lana di vetro                                                                                                 

Spessore: 4cm                                                                                                              

Peso specifico: 20 kg/m³ = 0.2kN/m³                                                                             

Volume: 0.04m x 1m x 1m = 0.04 m³                                                                            

Peso al metro quadro: 0.04 m³/m² x 0.2 kN/m³ = 0.008 kN/m²

 

Rivestimento in cartongesso                                                                                           

Spessore: 1cm                                                                                                              

Peso Specifico: 900 kg/m³ = 9 kN/m³                                                                             

Volume: 0.01m x 1m x 1m = 0.01m³                                                                              

Peso al metro quadro: 0.01 m³/m² x 9 kN/m³ = 0.09 kN/m²

 

Qp = (0.008 + 0.54 + 0.4 + 0.09 + 1.5) kN/m² = 2.54 kN/m²

 

Il carico accidentale (qa) rimane legato all’ambiente residenziale

Qa = 2 kN/m²

 

Con il carico ultimo derivato dal foglio e l’inserimento della luce è possibile ricavare il momento massimo della trave appoggiata.

Una volta scelto l’acciaio in barre B450C con resistenza caratteristica fyk= 450Mpa il foglio di calcolo ricava la resistenza di progetto con la formula

fyd= fyk/γm

Dove γm è il coefficiente di sicurezza di 1.15

Scelgo poi un calcestruzzo classe C60/75 con resistenza caratteristica fck = 60 Mpa. Il foglio di calcolo ricava la resistenza di progetto con la formula

Fcd= (α x fck)/ γm

Dove γm è il coefficiente di sicurezza di 1.5. α è un coefficiente che tiene conto del tempo pari a 0.85

Una volta impostata la dimensione della base della trave il foglio ricava l’altezza utile.

Come nel caso del legno, l’altezza utile dipende dal momento (al numeratore) e dalla resistenza di progetto del cemento per la base (al denominatore). Questo valore sotto radice viene moltiplicato per un valore r che tiene conto della compresenza dei due materiali nel cemento armato e quindi delle rispettive resistenze caratteristiche di acciaio e cemento.

hu = r  x √(Mx/ (fcd x b))

dove r = 2/(β(1-(β/3)))                                                                                                   

β= fcd/(fcd + (fyd/n))

Dalla somma dell’altezza utile con il copriferro che abbiamo scelto si ricava un’altezza minima di 35,19cm. Dunque si sceglie un’altezza ingegnerizzata H=40cm.

Il foglio di calcolo pesa la trave appena determinata e lo somma maggiorato con il coefficiente di sicurezza al carico ultimo. Otterremo nuovamente un’altezza minima di 36,41cm, cioè inferiore all’altezza ingegnerizzata. Dunque la sezione è verificata.

 

Ciao a tuttiiii!! Ci sono anche io!! Vi auguro una buonanotte prima dell'esercitazione numero uno!