Verifica di abbassamento di una mensola _ Esercitazione 3

Questa terza esercitazione consiste nel verifica della deformazione della mensola più sollecitata di un telaio in tre differenti tipologie: legno, acciaio e cemento armato.

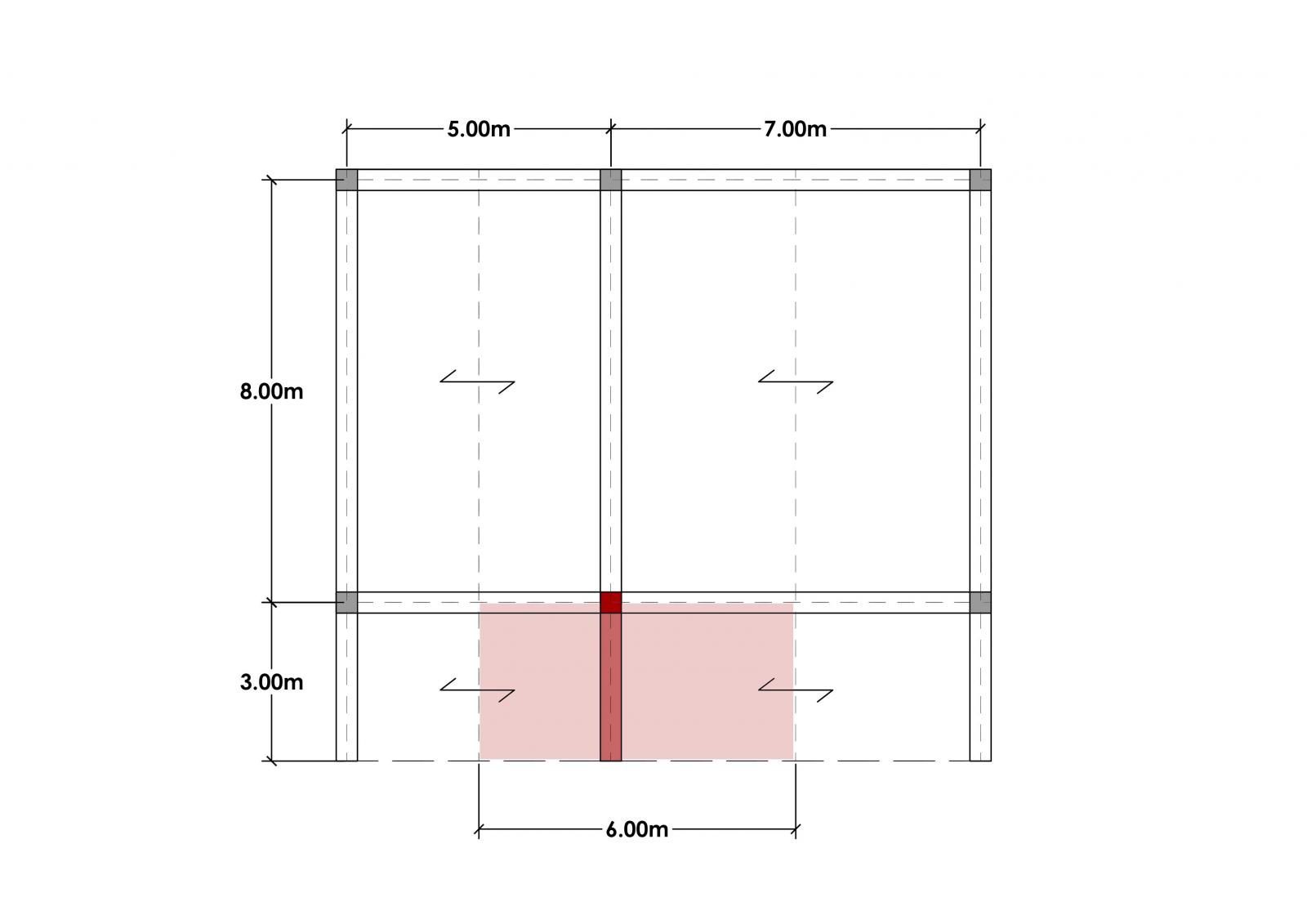
La mensola sottoposta a maggiore carico nella struttura presa in analisi è quella evidenziata in rosso: su di essa infatti grava il carico di solaio maggiore.

Luce: 3m

Interasse: 6m

Area di influenza: 18m²

LEGNO

Prima di calcolare e verificare la deformazione di una mensola è necessario dimensionare l’altezza della stessa. Consideriamo lo stesso pacchetto di solaio della prima esercitazione e, come nel caso della trave inflessa, inseriamo nel foglio i dati inerenti all’interasse, al carico strutturale, permanente e accidentale. In questo modo otteniamo il carico ultimo. qu = [(qs x 1.3) + (qp x 1.5) + (qa x 1.5)] x i

Inserendo la luce il foglio ricava il momento massimo: nel caso della mensola pari a Mmax= (qu x L²)/2

Una volta inserita la resistenza caratteristica (nel caso del legno lamellare GL24h pari a 24 Mpa), il coefficiente di sicurezza del materiale (per il legno lamellare γm=1.45) e il coefficiente correttivo per umidità e durata del carico (consideriamo una classe media con kmod=0.8) il foglio ricava la resistenza di progetto

fd = (kmod x fmk)/γm.

Impostando la base della trave, si determina l’altezza minima come nel caso della trave inflessa. Scegliamo dunque un’altezza ingegnerizzata.

Ora possiamo procedere al calcolo e alla verifica della deformazione.  Con i dati già presenti del foglio si ricava il momento di inerzia che, nel caso di una sezione rettangolare, è Ix= bh³/12. Possiamo anche calcolare il carico di esercizio pari alla somma dei carichi maggiorati con i relativi coefficienti di sicurezza (1 nel caso dei carichi strutturali e permanenti, 0.5 nel caso dei carichi accidentali) per l’interasse.

qe= [(qs x 1) + (qp x 1) + (qa x 1.5)] x i

Nel caso di una semplice mensola con carico uniformemente distribuito sappiamo che:

v(s) = 1/(EI) x [- (ql²s²)/4 – (qs⁴)/24 + (qls³)/6]

Poiché il massimo spostamento in una mensola avviene nell’estremo libero (cioè s=l) possiamo anche scrivere che

vmax= - (ql⁴)/8EI.

In realtà questo valore di spostamento massimo è un approssimazione: infatti esso viene associato ad una vera mensola mentre, in questo caso, la struttura si configura come aggetto di una trave appoggiata. Poiché la luce della trave appoggiata è 8m e l’aggetto è 3m (<8m/2) il vmax calcolato è maggiorato.

Dunque inserendo il modulo di elasticità E proprio del materiale nella tabella possiamo ricavare questo valore considerando come carico quello di esercizio (qe).

Affinchè la mensola sia verificata vmax < (1/250) x l. Dunque devo verificare che:

l/vmax >250.

In questo caso 439.70 > 250 dunque la mensola in legno è verificata!

ACCIAIO

Come nel caso del legno dobbiamo innanzitutto dimensionare l’altezza della mensola.  Inseriamo i dati inerenti l’interasse, la luce e i carichi del pacchetto di solaio considerato nella prima esercitazione. Il foglio di calcolo ricava carico ultimo e momento massimo della mensola come sopra. Inserendo la resistenza caratteristica del materiale (fyk=275Mpa per un acciaio S275) si ottiene la resistenza di progetto fd moltiplicando fyk per il coefficiente di sicurezza γm=1.05. Come nel caso della trave appoggiata imponendo σmax = fd e utilizzando la formula di Navier sappiamo che

Wxmin = Mx/fd

Dunque scegliamo nel sagomario una trave IPE con modulo di resistenza a flessione W immediatamente superiore. In questo caso un IPE 400. Dunque riportiamo sulla tabella i relativi valori di momento d’inerzia Ix e di peso della trave IPE 400 e il modulo di elasticità E proprio del materiale.

A differenza del legno il foglio calcola il carico di esercizio sommando ai carichi maggiorati e moltiplicati per l’interasse anche il peso della trave (nel caso del legno il peso della trave viene trascurato trattandosi di un materiale leggero). Dunque

qe= [(qs x 1) + (qp x 1) + (qa x 1.5)] x i + (peso trave x 1)

Con la stessa formula precedentemente utilizzata per il legno ricaviamo lo spostamento massimo: vmax= - (ql⁴)/8EI     (anche in questo caso maggiorato).

Anche in questo caso il rapporto l/vmax = 440.082 > 250 dunque la mensola in acciaio è verificata!

CEMENTO ARMATO

Anche per il cemento armato dobbiamo prima calcolare l’altezza della mensola. Inserendo interasse, luce e carichi del pacchetto di solaio in latero-cemento della prima esercitazione otteniamo carico ultimo e momento massimo. Una volta scelto il tipo di barre (B450C con resistenza caratteristica fyk= 450Mpa) e la classe del calcestruzzo (C60/75 con resistenza caratteristica fck = 60 Mpa) il foglio ricava le corrispettive resistenze di progetto corrette con i coefficienti di sicurezza.

Una volta impostata la dimensione della base della trave il foglio ricava l’altezza utile come nel caso della trave appoggiata. Questo valore sommato per il copriferro permette di ricavare un’altezza minima che possiamo ingegnerizzare. Il foglio ricava direttamente l’area (base per altezza) e il peso al metro quadro (area per peso specifico del cls).

Nella riga sottostante il foglio ricalcola il valore del carico ultimo aggiungendo a quello precedente il peso della trave moltiplicato per il coefficiente per carichi strutturali pari a 1.3. Viene ricalcolato dunque il momento massimo e, mantenendo i valori delle resistenze e delle dimensioni scelte nel progetto, ricalcola l’altezza minima. Anche con il peso della trave l’altezza minima rimane inferiore al valore di altezza ingegnerizzata che avevamo scelto dunque l’altezza è verificata.

Ora possiamo procedere con il calcolo e la verifica dello spostamento massimo della mensola. Come nel caso dell’acciaio il foglio calcola il carico di esercizio sommando ai carichi maggiorati e moltiplicati per l’interasse anche il peso della trave.

qe= [(qs x 1) + (qp x 1) + (qa x 1.5)] x i + (peso trave x 1)

Inserendo il valore del modulo di elasticità E proprio del materiale e calcolando il momento d’inerzia Ix per una sezione rettangolare (come nel caso del legno Ix= bh³/12) il foglio ricava lo spostamento massimo

vmax= - (ql⁴)/8EI    (anche in questo caso maggirato)

Anche in questo caso il rapporto l/vmax = 286.21> 250 dunque la mensola in cemento armato è verificata!