ESECITAZIONE 5_RIPARTIZIONE FORZE SISMICHE

La quinta esercitazione consiste nel calcolo della ripartizione di una forza orizzontale (sismica o del vento) agente su una struttura a telai Shear-Type in cemento armato utilizzando il metodo delle rigidezze.

La struttura presa in analisi è caratterizzata da 3 telai orizzontali e 4 telai verticali e i pilastri sono di dimensioni 30x50cm, di altezza 3,50m.

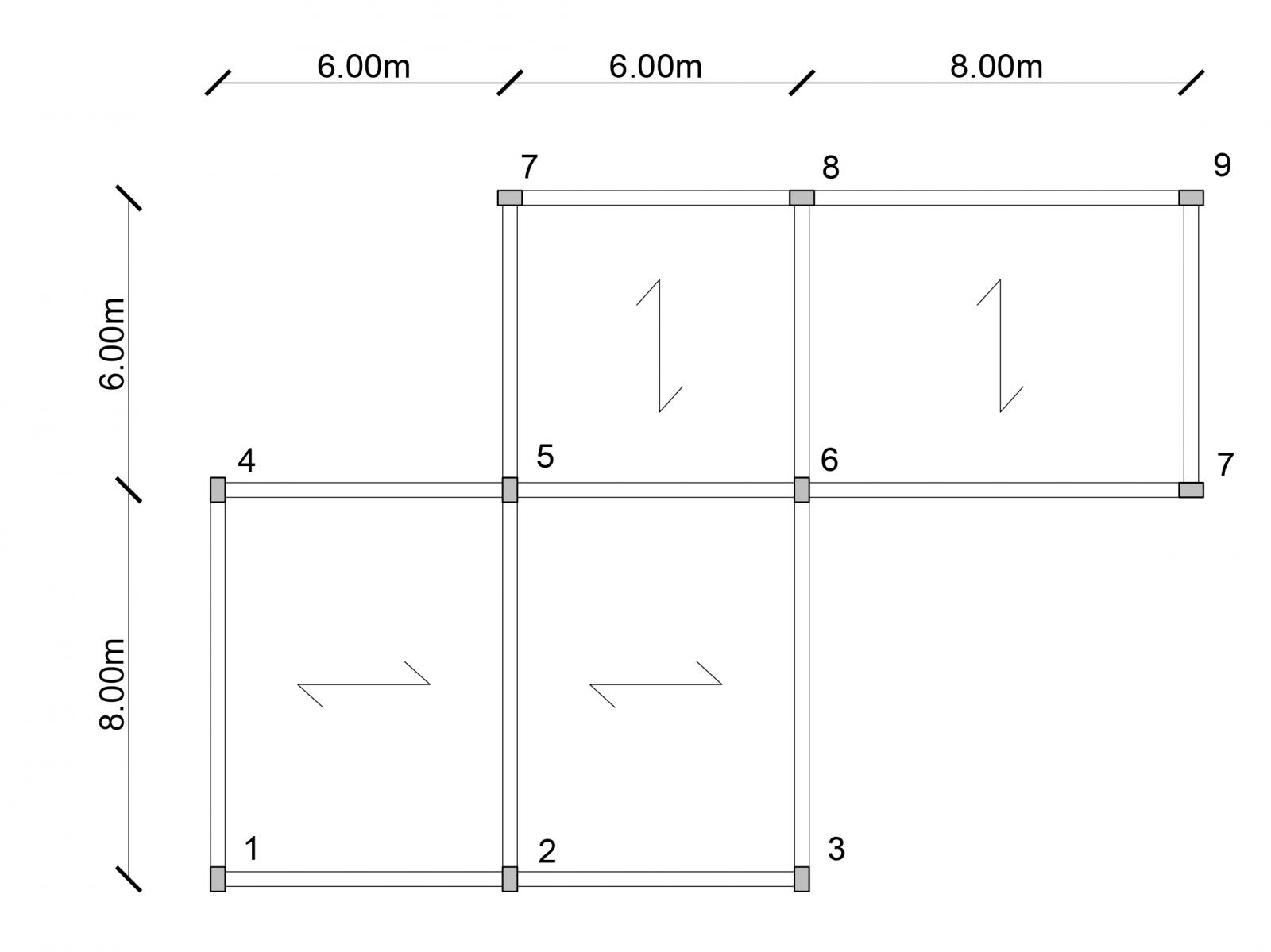
I controventi sono per il solaio vincoli cedevoli elasticamente quindi vengono rappresentati nel piano dell’impalcato come molle di adeguata rigidezza.

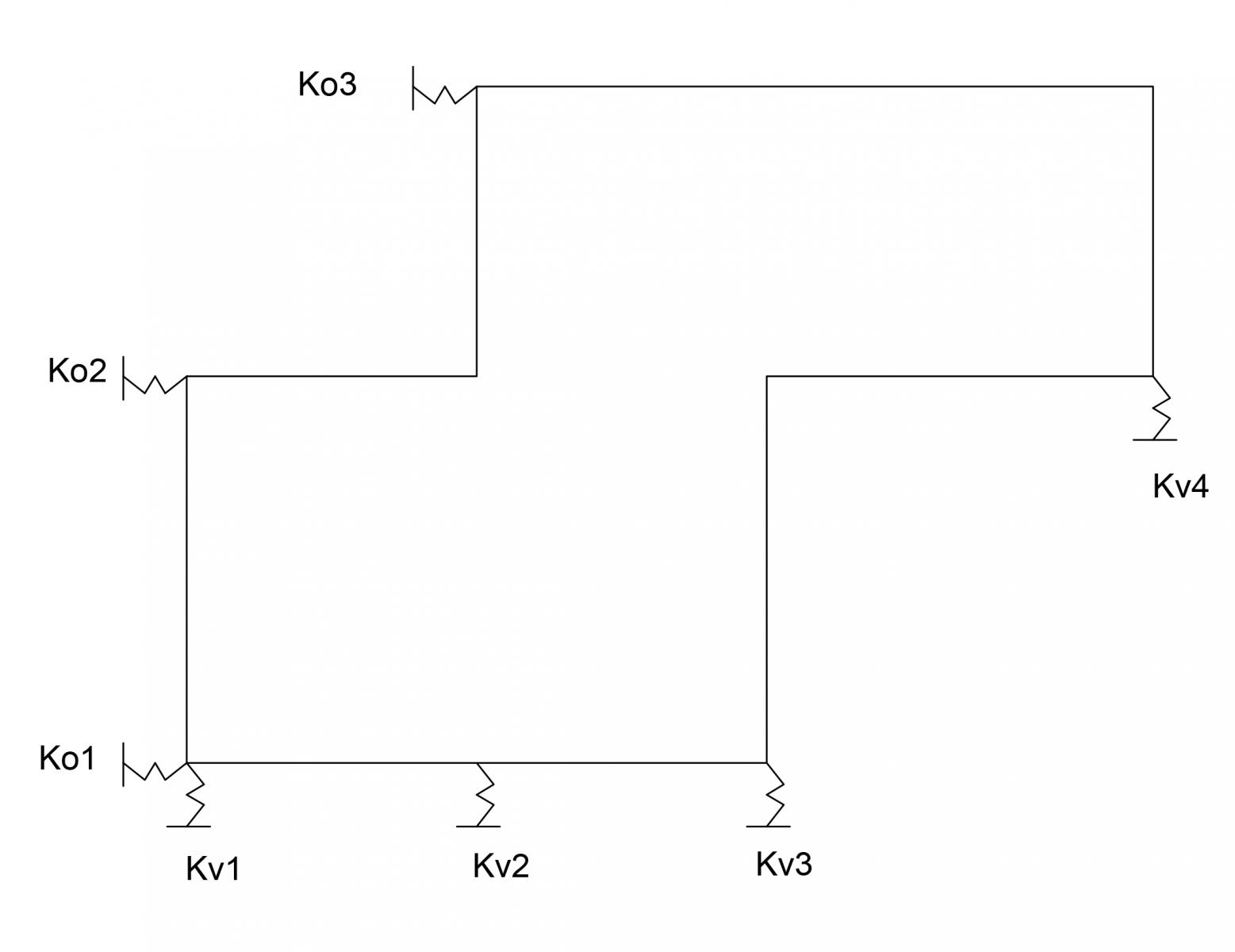
STEP1

Poichè i telai sono modellizzati come degli Shear-Type sappiamo che ogni ritto contribuirà alla rigidezza traslante con un contributo di 12EI/h³.

K=(12EI₁)/ h³ + (12EI₂) h³+ … + (12EI_n)/h³

Quindi per calcolare la rigidezza traslante di ogni controvento sarà necessario inserire nel foglio excel il modulo di Young proprio del materiale(E), l’altezza dei pilastri (h) e il loro modulo d’inerzia (I):

Imax=bh³/12=(30cm)*(50cm)³/12= 312500cm⁴

Imin= hb³/12=(50cm)*(30cm)³/12= 112500cm⁴

STEP2

In questo step vengono calcolate le distanze dei controventi dal punto O, origine del sistema di riferimento.

STEP3

Per il calcolo del centro di massa è necessario suddividere l’impalcato in figure elementari, calcolare le rispettive aree e individuare le coordinate del loro centro geometrico. Dunque sarà possibile calcolare il centro di massa (che nel caso di un impalcato con densità di massa uniforme coincide con il centro d’area)

XG = [(A₁ * x_G1)+(A₂ * x_G2)]/Atot

YG = [(A₁ * y_G1)+(A₂ * y_G2)]/Atot

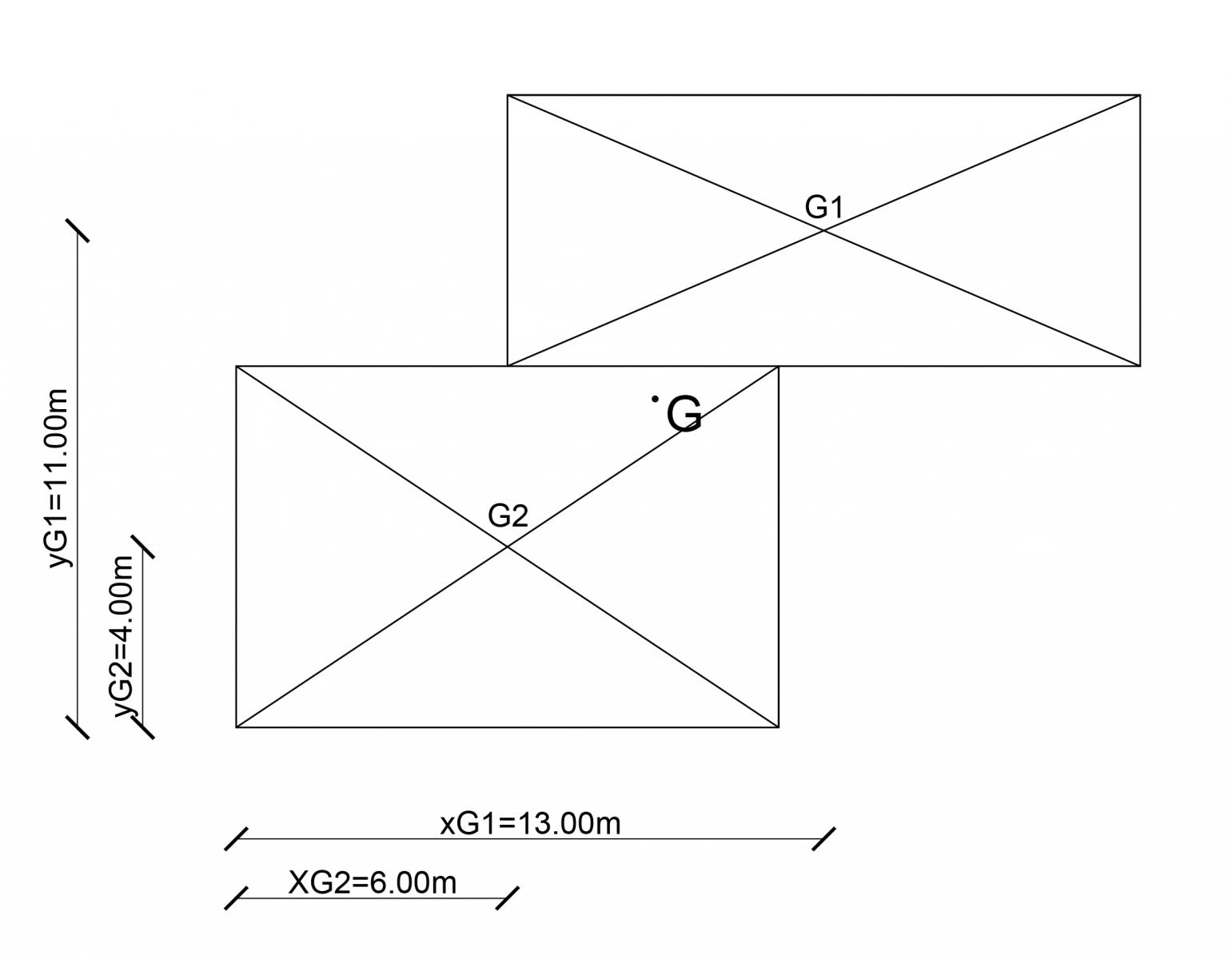
STEP4

Oltre a calcolare la rigidezza totale orizzontale (k_otot) e verticale(k_vtot), il foglio di calcolo ricava le coordinate del centro delle rigidezze

XC = [(k_v1*d_v1)+ (k_v2*d_v2)+ (k_v3*d_v3)+ (k_v4*d_v4)]/k_vtot

YC = [(k_o1*d_o1)+ (k_o2*d_o2)+ (k_o3*d_o3)]/k_otot

Ora è dunque possibile rappresentare nell’impalcato il centro di massa G e il centro delle rigidezze C.

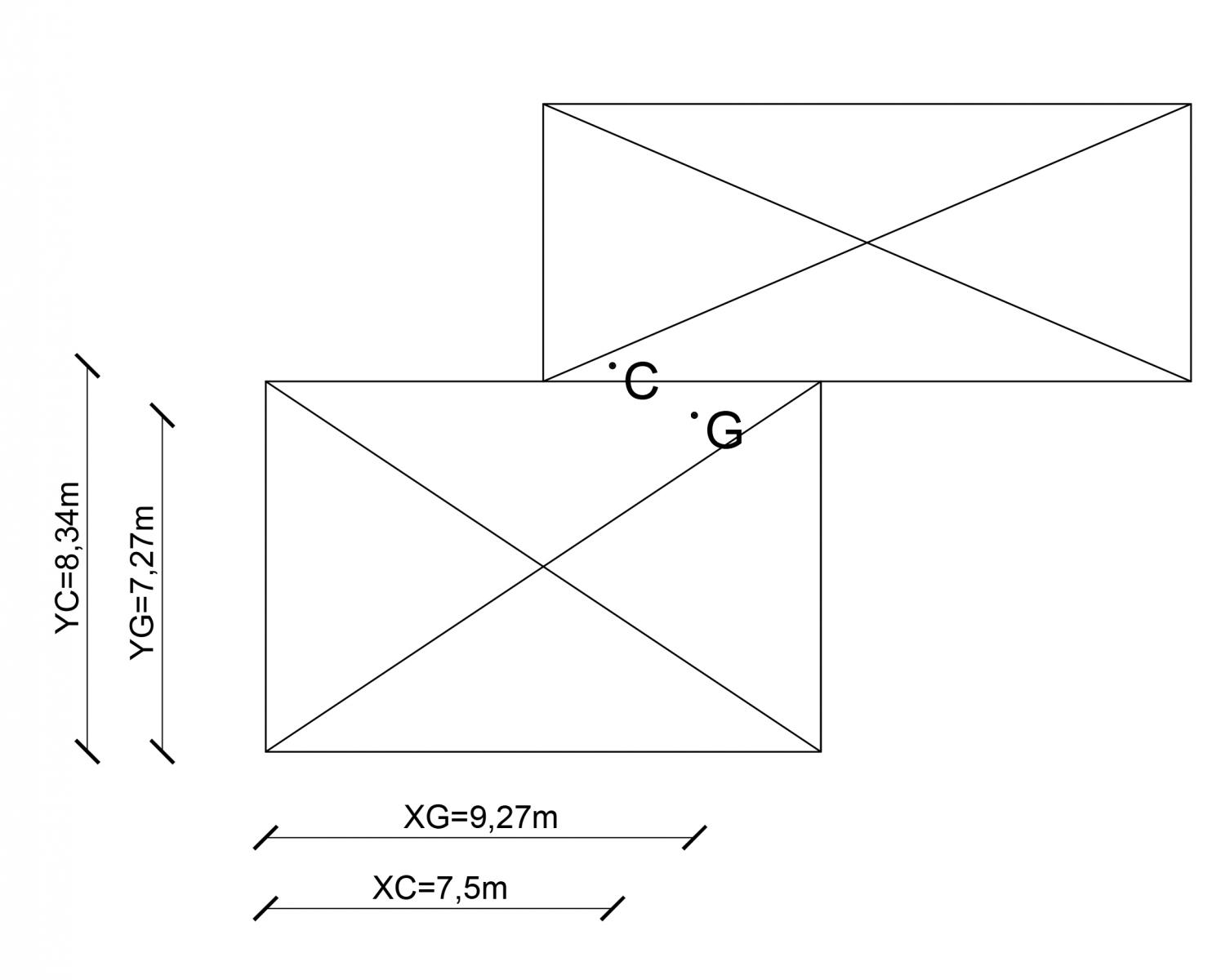
Sapendo che la forza sismica verrà applicata al centro di massa, possono essere fatte delle osservazioni.

Se la forza sismica è orizzontale allora l’impalcato trasla di una quantità u e ruota in modo antiorario.

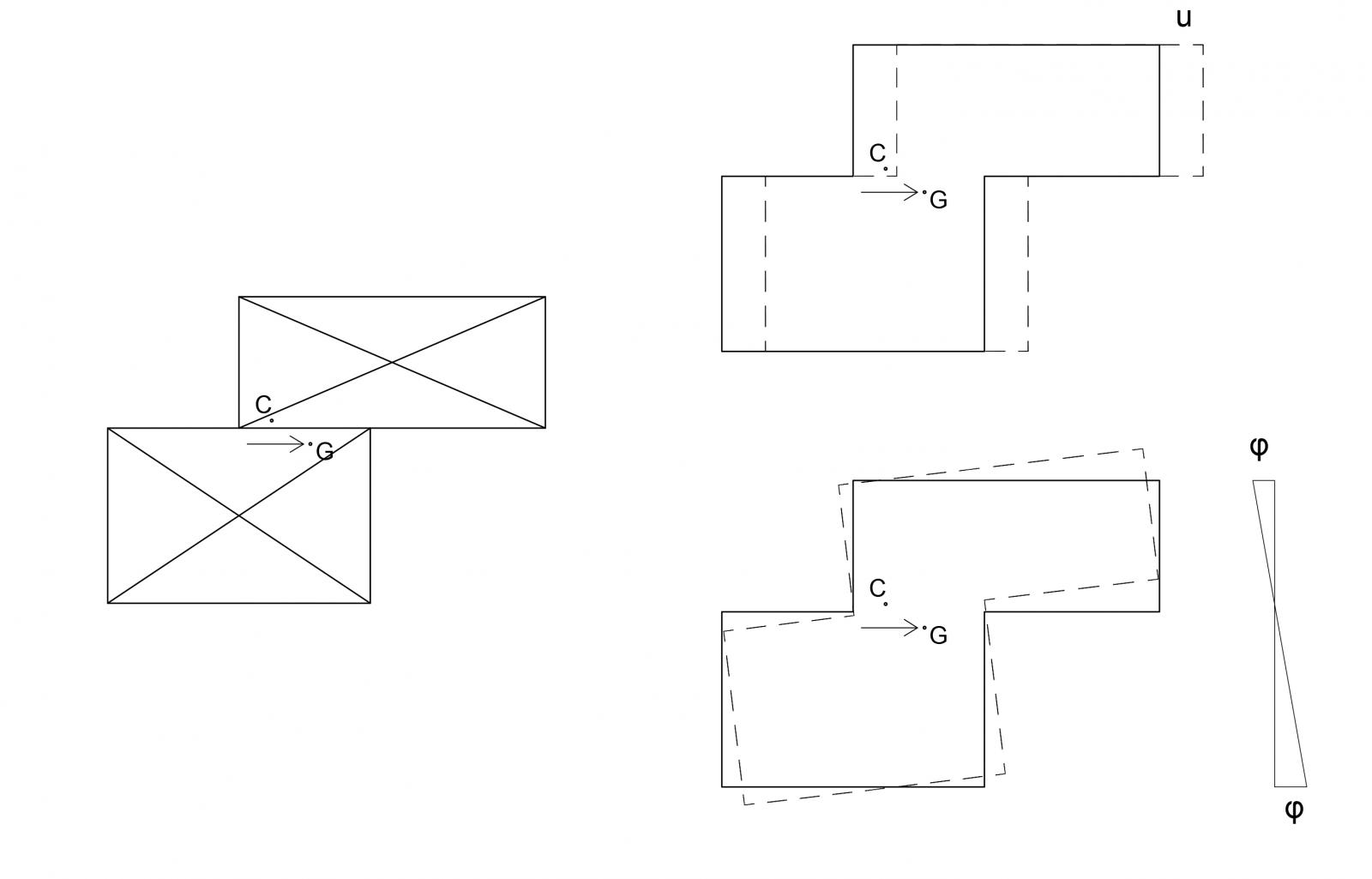
Se la forza sismica è verticale allora l’impalcato trasla di una quantita v e ruota in modo antiorario.

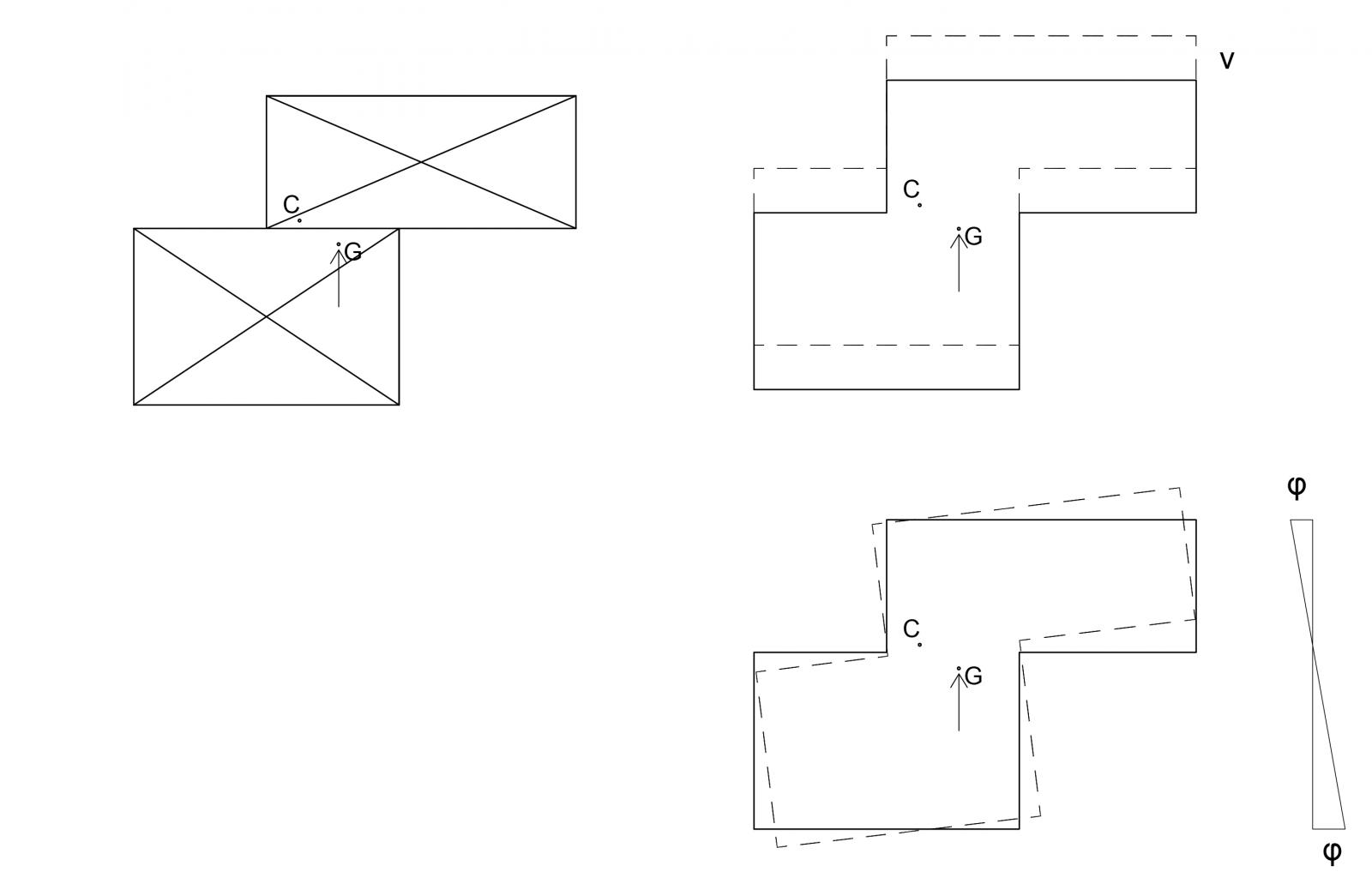
In questo step vengono inoltre ricalcolate le distanze dei controventi dal centro di rigidezza per ricavare la rigidezza torsionale k_φ

k_φ = (k_v1*dd_v1²)+ (k_v2*dd_v2²)+ (k_v3*dd_v3²)+ (k_v4*dd_v4²)+(k_o1*dd_o1²)+ (k_o2*dd_o2²)+ (k_o3*dd_o3²)

STEP5

Inserendo i valori dei carichi strutturali (qs), permanenti (qp) e accidentali (qa) è possibile ricavare il carico totale permanente (G) e il carico totale accidentale (Q)

G=(q_s + q_p) * A_tot

Q=q_a * A_tot

Dunque calcoliamo il peso sismico W introducendo un coefficiente di contemporaneità ψ_2j(che in ambienti residenziali è pari a 0.3).

W= G + ψ_{2j *} Q

Introducendo un coefficiene di intensità sismica c(a Roma pari a 0,10) è possibile calcolare la forza che applicheremo al centro delle masse

F= W *c

STEP6

Oltre il calcolo della traslazione orizzontale u

u=F/ k_otot

viene calcolato il momento generato dalla forza sismica

M=F* (YG-YC)

Dunque, conoscendo anche k_φ,  si ricava la rotazione φ

Φ = M/ k_φ

Quindi è possibile capire come si ripartisce la forza sismica lungo x sui controventi.

La reazione elastica di quelli orizzontali sarà il prodotto della rigidezza traslante per la somma degli spostamenti (traslazione orizzontale e rotazione per braccio).

F_{o_n}= k_{o_n} *(u + φ*dd _{o_n})

La reazione elastica di quelli verticali sarà il prodotto della rigidezza traslante per lo spostamento (rotazione per braccio).

F_{v_n}= k_{v_n} * φ*dd _{v_n}

STEP7

Oltre il calcolo della traslazione verticale v

v=F/ k_vtot

viene calcolato il momento generato dalla forza sismica

M=F* (XG-XC)

Dunque, conoscendo anche k_φ,  si ricava la rotazione φ

Φ = M/ k_φ

Quindi è possibile capire come si ripartisce la forza sismica lungo y sui controventi.

La reazione elastica di quelli orizzontali sarà il prodotto della rigidezza traslante per lo spostamento (rotazione per braccio).

F_{o_n}= k_{o_n} *φ*dd _{o_n})

La reazione elastica di quelli verticali sarà il prodotto della rigidezza traslante per la somma degli spostamenti (traslazione verticale e rotazione per braccio).

F_{v_n}= k_{v_n} * (v + φ*dd _{v_n})