Dimensionamento di un pilastro_ Esercitazione 4

Questa esercitazione consiste nel dimensionamento del pilastro più sollecitato in un telaio nelle tre diverse tecnologie: legno, acciaio e cemento armato.

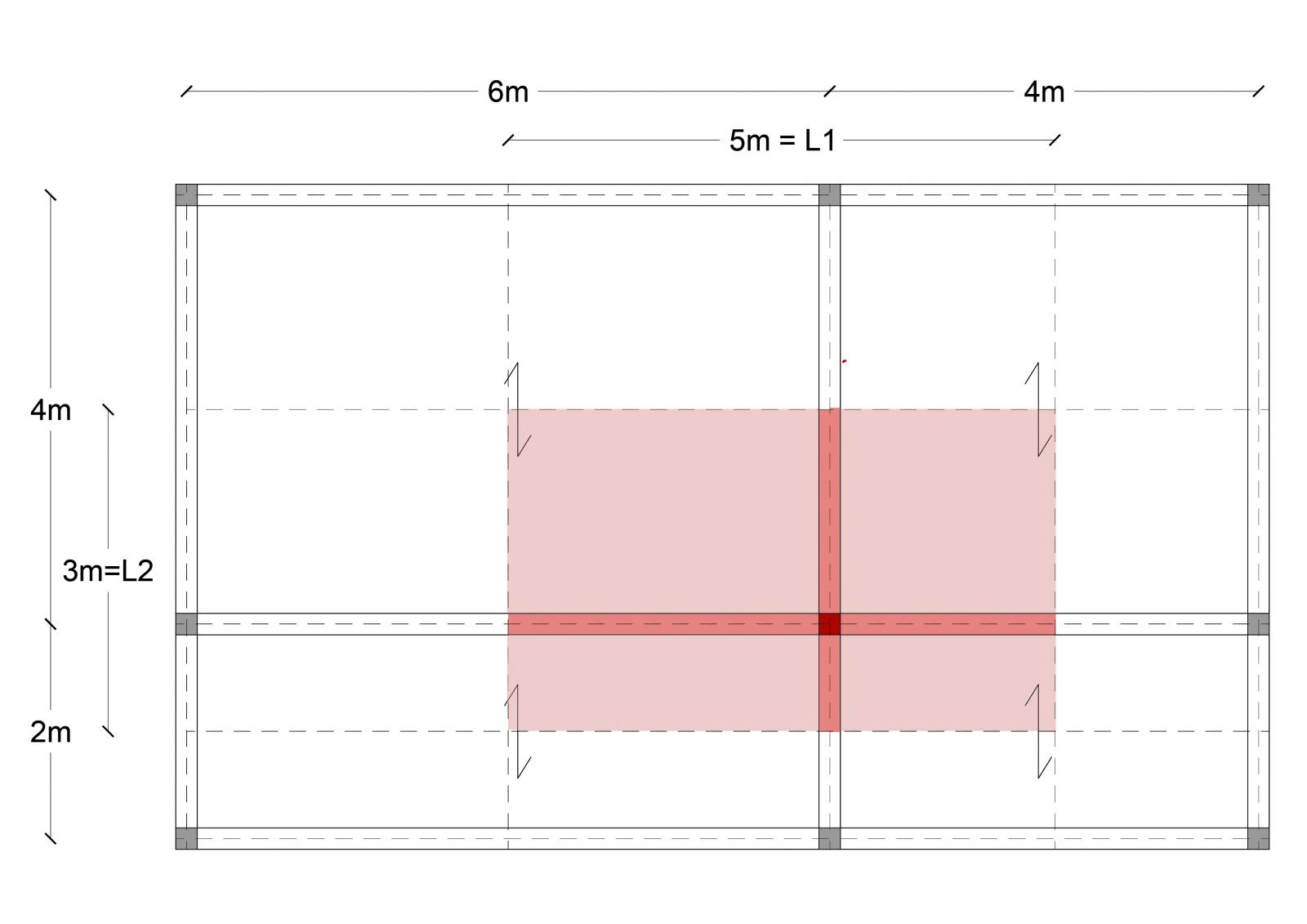
L1 = 7m

L2 = 5m

Area di influenza = L1 x L2 = 35m²

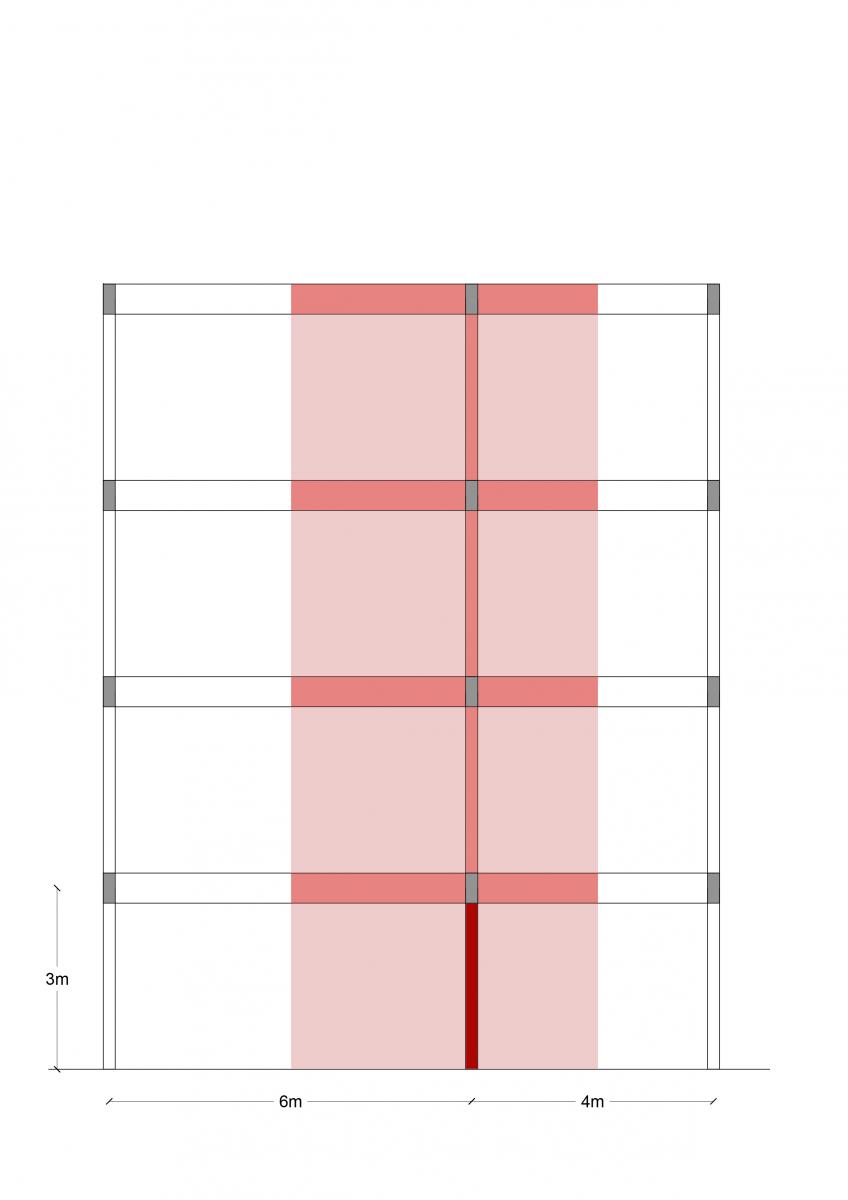
Numero piani = 4

 

Il pilastro sottoposto a maggiore sforzo normale nella struttura presa in analisi è quello evidenziato in rosso: su di esso infatti grava il carico di travi e solaio per la maggiore area di influenza che dovrà essere moltiplicato per il numero dei piani sovrastanti.

LEGNO

 

Contributo delle travi

Si calcola moltiplicando il peso unitario di ciascuna trave (considero il peso unitario della trave calcolato nella prima esercitazione) per l’interasse, moltiplicando il valore ottenuto per il coefficiente di sicurezza per carichi strutturali pari a 1.3.

 

Qtravi = (Peso unitario trave1 x  L1 x 1.3) + (Peso unitario trave2 x L2 x 1.3)

 

Contributo del solaio

Si ottiene moltiplicando la somma dei carichi (strutturali, permanenti e accidentali calcolati nella prima esercitazione e maggiorati dei rispettivi coefficienti di sicurezza) per l’area di influenza.

 

Qsolaio = [(qs x1.3) + (qp x 1.5) + (qa x 1.5)] x area di influenza

 

È dunque possibile calcolare lo sforzo normale agente sul pilastro del piano terra

N = (Qtravi + Qsolaio) x 4 piani

 

Un pilastro sottoposto a compressione può essere soggetto a rottura per schiacciamento del materiale o soggetto all’innesco del fenomeno di instabilità.

 

Per evitare il fenomeno di rottura per schiacciamento la tensione massima nel pilastro (σmax) deve essere minore della resistenza a compressione di progetto del materiale (fcd).

 

σmax < fcd

 

Imponendo σmax = fcd possiamo ricavare l’area minima della sezione ovvero il valore minimo che deve avere l’area per non essere soggetta a rottura.

Infatti poiché

σmax = N/Amin

fcd = N/Amin

 

In fase progettuale si è scelto per il pilastro un legno lamellare GL24h con resistenza caratteristica fmk pari a 24 Mpa. La resistenza di progetto fd che viene calcolata dal foglio tiene conto della resistenza caratteristica corretta con alcuni parametri:

fd = (kmod x fmk)/γm

γm è un coefficiente di sicurezza del materiale: in questo caso per il legno lamellare γm = 1.45.

Kmod è un coefficiente correttivo che tiene conto della durata di carico (consideriamo una durata media) e dell’umidità della struttura (consideriamo una classe media).

 

dunque ora, conoscendo il valore di fcd, è possibile calcolare l’area minima con la formula inversa.

Amin =N/fcd

 

Affinché, invece, nel pilastro non si inneschi un fenomeno di instabilità lo sforzo nomale deve essere inferiore allo sforzo critico euleriano.

 

N<Ncrit

 

Sappiamo che

Ncrit= (π²EImin)/(βl)²

 

Poiché

βl = l0 (lunghezza libera di inflessione)

Imin=Aρmin²

 

Ncrit = (π²EAρmin²)/(l0)²

 

Poiché λ=l0/ρmin

Ncrit = π²EA/ λ²

 

Allo sforzo critico euleriano è possibile associale una tensione critica

σcrit = Ncrit/A = π²E/ λ²

 

Per evitare il fenomeno di instabilità la tensione massima nel pilastro (σmax) deve essere minore della tensione critica (σcrit)

σmax < σcrit

 

Poiché abbiamo imposto

σmax = fcd

allora

 

fcd < σcrit    (prima di inflettersi per instabilità, il pilastro si rompe. Questa soluzione è

                       ottimale poiché l’instabilità non è controllabile)

fcd < π²E/ λ²

λ² < π²E/fcd

λmax = π √(E/fcd)

Dunque una volta inseriti i valori del modulo di elasticità (E) proprio del materiale e la resistenza di progetto (fcd), il foglio di calcolo ricava la snellezza massima del pilastro (λmax).

Ma, poiché

λ = l0/ρmin

 

ρmin = l0/λ

 

Dunque una vola inseriti i valori di β e della lunghezza del pilastro (l), si ottiene il valore della lunghezza libera di inflessione (l0) che il foglio di calcolo dividerà per la snellezza massima appena ricavata: dunque si ottiene il raggio di inerzia minimo. Ricordando che nelle sezioni rettangolari

ρmin = √(1/12) b

possiamo ricavare la base tramite la formula inversa:

bmin = 2√3 ρmin

Una volta ingegnerizzata calcoliamo l’altezza minima

hmin= Amin/b

Una volta ingegnerizzata anche l’altezza il foglio ricalcola l’area e il momento d’inerzia di design. Dunque sarà necessario verificare che l’area di design sia maggiore dell’area minima precedentemente calcolata.

 

ACCIAIO

Per calcolare lo sforzo normale agente sul pilastro si sommano nuovamente i contributi di travi e solaio all’interno dell’area di influenza e si moltiplicano per il numero di piani.

Anche in questo caso, per ricavare il contributo delle travi, si sceglie il peso unitario delle travi della prima esercitazione e si moltiplica per l’interasse relativo e per il coefficiente si sicurezza strutturale.

Qtravi = (Peso unitario trave1 x  L1 x 1.3) + (Peso unitario trave2 x L2 x 1.3)

 

Poi per ricavare il contributo del solaio si scelgono i valori dei carichi strutturali, permanenti e accidentali della prima esercitazione, si maggiorano con i relativi coefficienti di sicurezza e la loro somma viene moltiplicata per l’area di influenza.

Qsolaio = [(qs x1.3) + (qp x 1.5) + (qa x 1.5)] x area di influenza

 

È dunque ora possibile calcolare lo sforzo normale agente sul pilastro del piano terra

N = (Qtravi + Qsolaio) x 4 piani

 

Avendo scelto per la trave un acciaio S275 con resistenza caratteristica fyk=275Mpa, si ricava la resistenza di progetto correggendo quella caratteristica con un coefficiente di sicurezza γm=1.05.

fyd = fyk/γm

Dunque imponendo σmax = fyd possiamo ricavare l’area minima della sezione come sopra:

 

Amin= N/fyd

 

Come per il legno inserendo i dati relativi al modulo di elasticità (E) relativo al materiale e la resistenza di progetto (fyd) appena calcolata, il foglio ricava il valore della snellezza massima

λmax = π √(E/fcd)

Inserendo poi i valori di β e della lunghezza del pilastro (l), si ottiene il valore della lunghezza libera di inflessione (l0) che il foglio di calcolo dividerà per la snellezza massima appena ricavata: dunque si ottiene il raggio di inerzia minimo.

ρmin = l0/λ

 

Ora, poiché la sezione di un pilastro in acciaio non è rettangolare, bensì sarà un profilo HEA possiamo calcolare il momento di inerzia minimo con la formula

Imin = A x ρmin²

Ora sarà possibile scegliere su un sagomario l’HEA che possiederà un momento inerzia, un raggio di inerzia e un area immediatamente superiori a quelle trovate. Il foglio ricalcolerà la snellezza con i nuovi valori e si dovrà verificare che non superi il valore 200.

 

CEMENTO ARMATO

Per calcolare lo sforzo normale agente sul pilastro si sommano nuovamente i contributi di travi e solaio all’interno dell’area di influenza e si moltiplicano per il numero di piani.

Anche in questo caso, per ricavare il contributo delle travi, si sceglie il peso unitario delle travi della prima esercitazione e si moltiplica per l’interasse relativo e per il coefficiente si sicurezza strutturale.

Qtravi = (Peso unitario trave1 x  L1 x 1.3) + (Peso unitario trave2 x L2 x 1.3)

 

Poi per ricavare il contributo del solaio si scelgono i valori dei carichi strutturali, permanenti e accidentali della prima esercitazione, si maggiorano con i relativi coefficienti di sicurezza e la loro somma viene moltiplicata per l’area di influenza.

Qsolaio = [(qs x1.3) + (qp x 1.5) + (qa x 1.5)] x area di influenza

 

È dunque ora possibile calcolare lo sforzo normale agente sul pilastro del piano terra

N = (Qtravi + Qsolaio) x 4 piani

 

Scelgo poi un calcestruzzo classe C60/75 con resistenza caratteristica fck = 60 Mpa.

Il foglio di calcolo ricava la resistenza di progetto con la formula

Fcd= (α x fck)/ γm

Dove γm è il coefficiente di sicurezza di 1.5

e α è un coefficiente che tiene conto del tempo pari a 0.85

 

Dunque imponendo σmax = fcd possiamo ricavare l’area minima della sezione come sopra:

 

Amin= N/fcd

 

Come per il caso di legno e acciaio inserendo i dati relativi al modulo di elasticità (E) relativo al materiale e la resistenza di progetto (fyd) appena calcolata, il foglio ricava il valore della snellezza massima

λmax = π √(E/fcd)

Inserendo poi i valori di β e della lunghezza del pilastro (l), si ottiene il valore della lunghezza libera di inflessione (l0) che il foglio di calcolo dividerà per la snellezza massima appena ricavata: dunque si ottiene il raggio di inerzia minimo.

ρmin = l0/λ

 

Come nel caso del legno possiamo ricavare la base tramite la formula:

bmin = 2√3 ρmin

Una volta ingegnerizzata calcoliamo l’altezza minima

hmin= Amin/b

Una volta ingegnerizzata anche l’altezza, il foglio ricalcola l’area e il momento d’inerzia di design.

 

Per il pilastro in calcestruzzo è necessario aggiungere un ulteriore verifica. Infatti il pilastro non sarà soggetto a sola compressione, ma anche a flessione derivante dall’incastro che avremo nel nodo trave pilastro. Dunque per verificare a presso-flessione dovremo controllare che la tensione massima dovuta sia allo sforzo normale che al momento flettente sia inferiore alla tensione di progetto.

σmax = N/A + Mt/Wmax < fcd

Dunque il foglio, avendo tutti i dati, calcola automaticamente il modulo di resistenza a flessione Wmax

Wmax= bh²/6

E il momento all’estremo della trave e quindi sulla testa del pilastro che viene calcolato come

Mt= (qt x Lp²)/12

Dove qt (calcolato da foglio) è il carico di solaio distribuito sulla trave principale: quindi si sommano i carichi strutturali, permanenti e accidentali maggiorati per l’interasse tra le travi principali ovvero qt = [(qs x 1.3) + (qp x 1.5) + (qa x 1.5)] x Ls.

Dunque il foglio di calcolo ricava il σmax e verifica se risulta minore di fcd. Se non risulta verificato sarà necessario aumentare gradualmente le dimensioni del pilastro fino alla verifica di questa condizione.