ESERCITAZIONE 2 - Dimensionamento di una struttura reticolare spaziale in acciaio

Iniziamo col definire il modello della struttura reticolare spaziale in SAP2000:

1. Apriamo il software e andiamo su File → New model
2. Impostiamo le unità di misura del modello e scegliamo il template più comodo che in questo caso risulta essere la griglia spaziale triortogonale
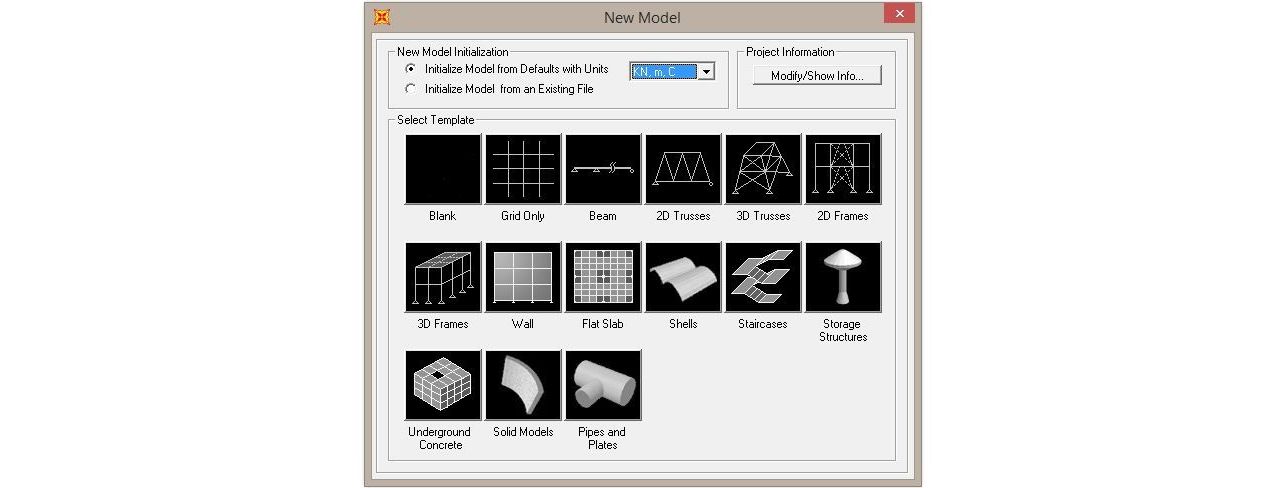
3. Della griglia andremo a definire il numero di linee rette nelle direzioni triortogonali x, y, z e la loro spaziatura nei piani triortogonali xy, yz, zx. Con la griglia definita andremo a realizzare il modello di una struttura reticolare spaziale avente tante aste quanto i segmenti definiti dalle linee di griglia più un numero di aste necessarie a 'triangolare' tutta la struttura (al fine di sfruttare la rigidezza del telaio triangolare)
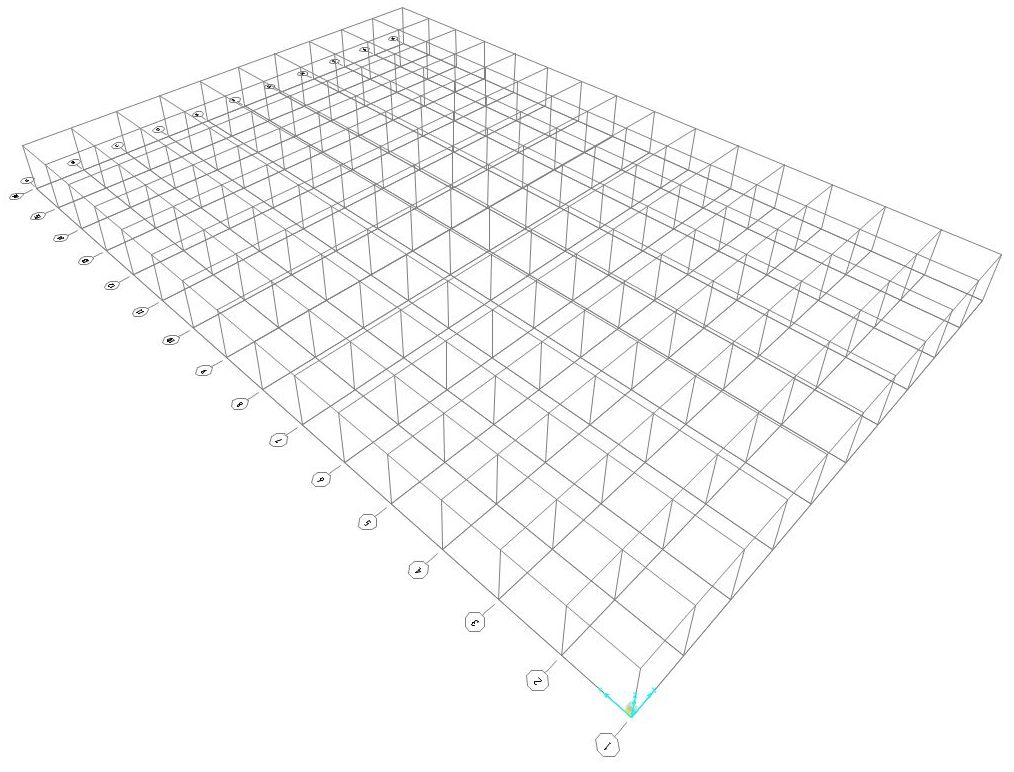
4. Andiamo quindi a disegnare come ci è più comodo non tutte ma un certo numero di aste che poi andremo a copiare e incollare in una delle due direzioni di base
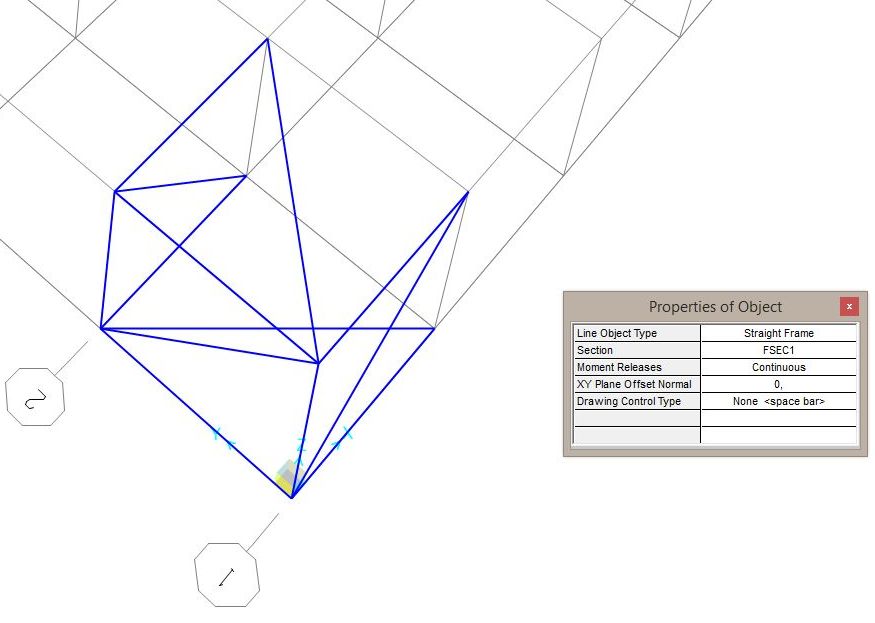
5.  Poi, sempre copiando e incollando nell'altra direzione di base andremo a definire tutte le aste componenti la struttura
6.  Verifichiamo di non aver erroneamente sovrapposto più aste attraverso il comando Edit → Show Duplicates 
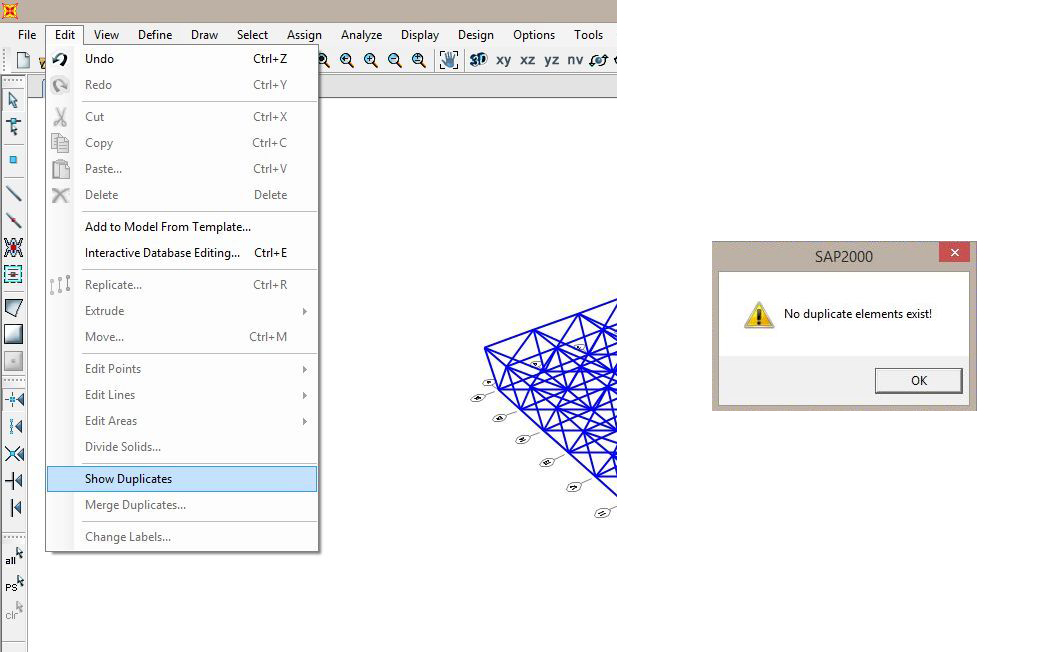
7.  Un altro accorgimento è quello di fondere i nodi entro una certa distanza di tolleranza (cioè nel caso in cui non tutte le aste che dovrebbero convergere in un nodo convergono in quel nodo ma convergono in un altro nodo ad una distanza molto piccola dal primo, distanza sicuramente inferiore alla tolleranza che andremo ad impostare). Selezioniamo dunque tutta la struttura e andiamo su Edit → Edit Points → Merge Joints ed impostiamo la Merge Tolerance
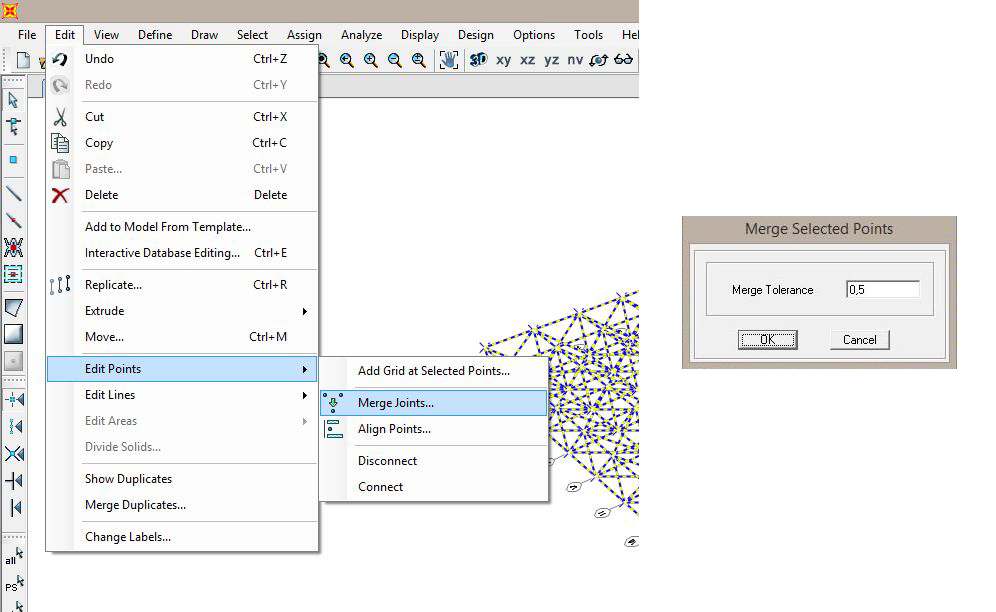
8. Imponiamo i vincoli: scegliamo i nodi attraverso i quali la struttura sarà vincolata (io ne ho scelti 3 disallineati, ossia il numero minimo affinche non ci sia labilità), li selezioniamo e andiamo a definirne i gradi di vincolo attraverso il comando Assign → Joint → Restraints... e andando a vietare la traslazione nelle tre direzioni 
9.  Trattandosi del modello di una struttura reticolare, cioè una struttura in cui è presente solo sforzo normale, dobbiamo imporre che tutti i suoi nodi siano delle cerniere. Selezioniamo nuovamente tutte le aste e andiamo su Assign → Frame → Releases/Partial fixity... e rilasciamo momento22 e momento33 all'inizio e alla fine delle aste 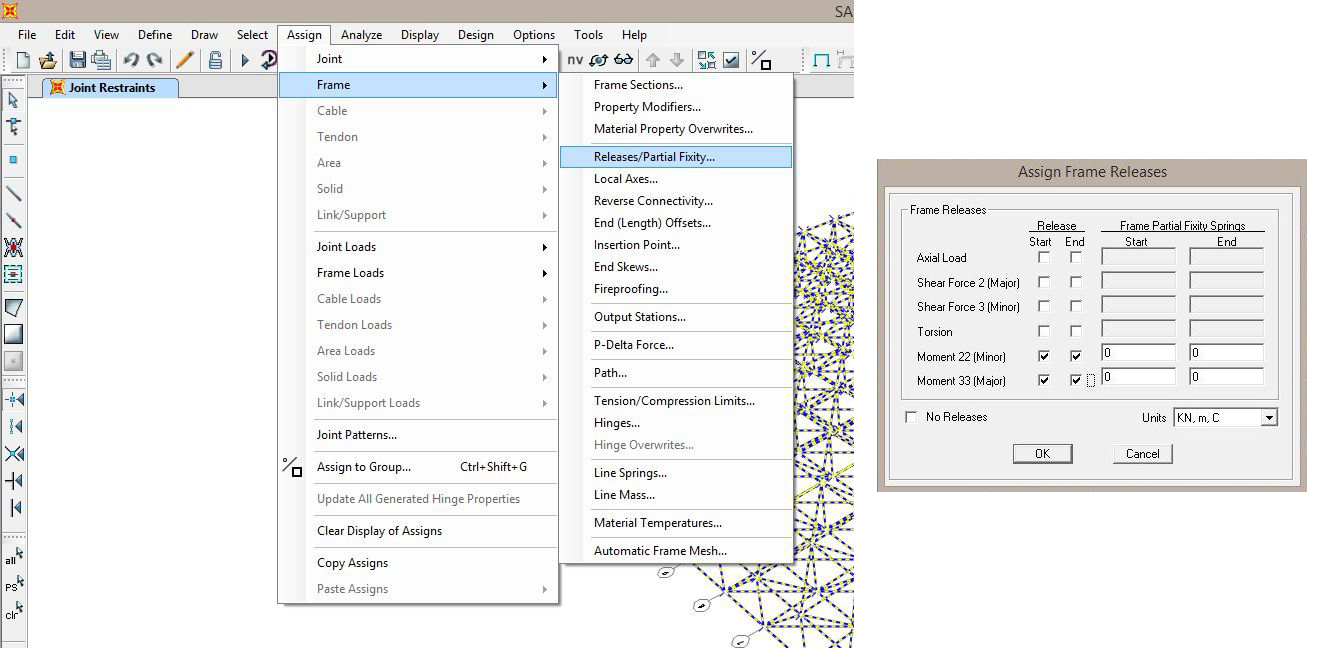Nel modello le aste appariranno come se distanziate dai nodi
10. Definiamo le caratteristiche materiche e geometriche delle nostre aste. Selezioniamo tutte le aste del modello e andiamo su Assign → Frame → Frame Sections... e poi su Add New Property...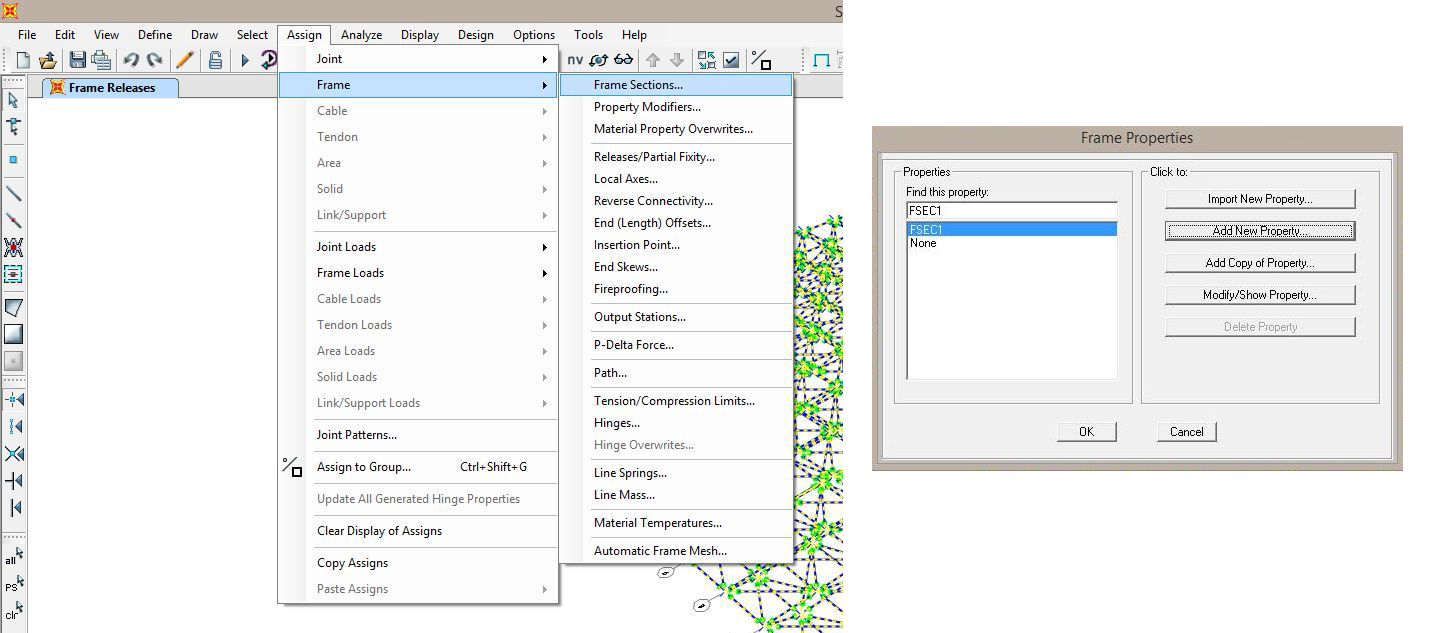...e andiamo a definire materiale, profilo e caratteristiche del profilo (in questo caso ho scelto un tubo circolare di diametro esterno 200mm e di spessore 10mm)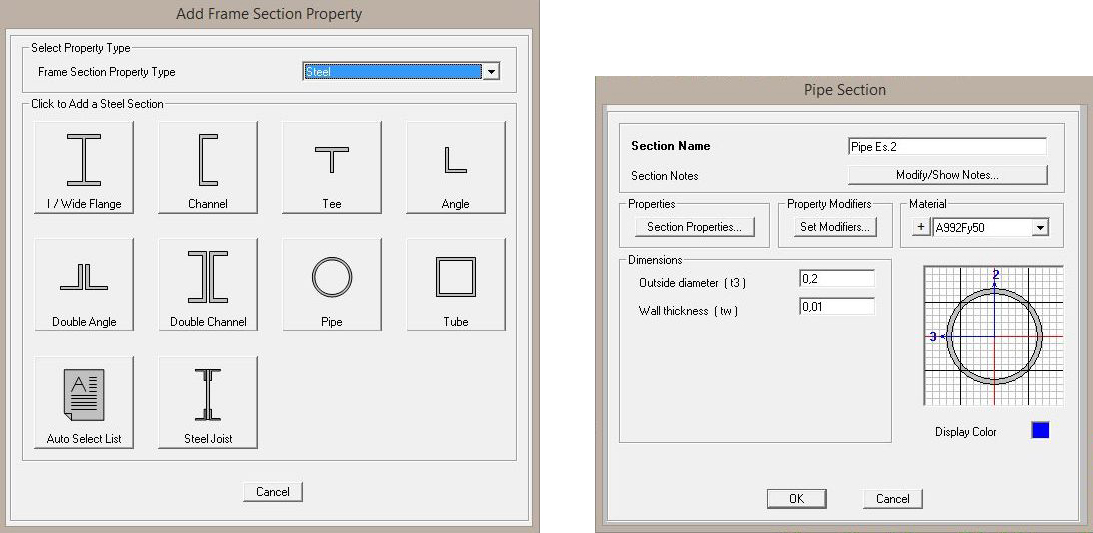
11. Definiamo i carichi agenti sulla struttura da Define → Load Patterns... aggiungiamo un nuovo modello di carico (Add New Load Pattern) lo nominiamo ed impostiamo il peso proprio pari a zero (colonna Self Weight Multiplier)
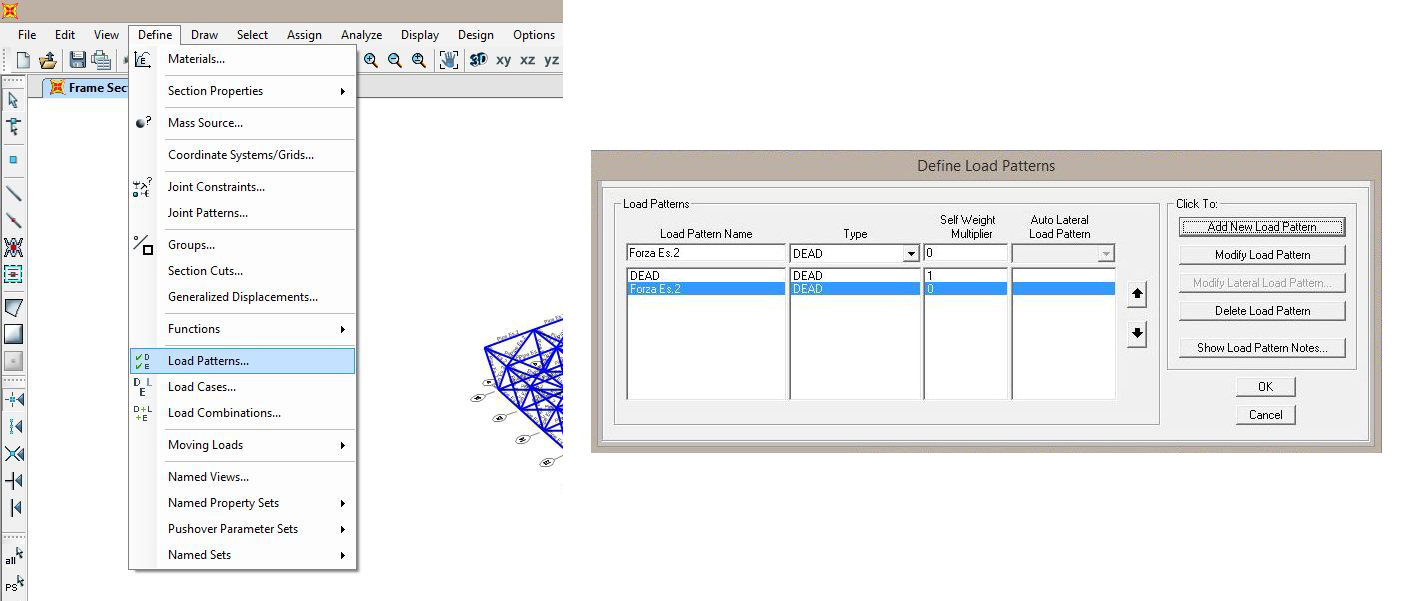
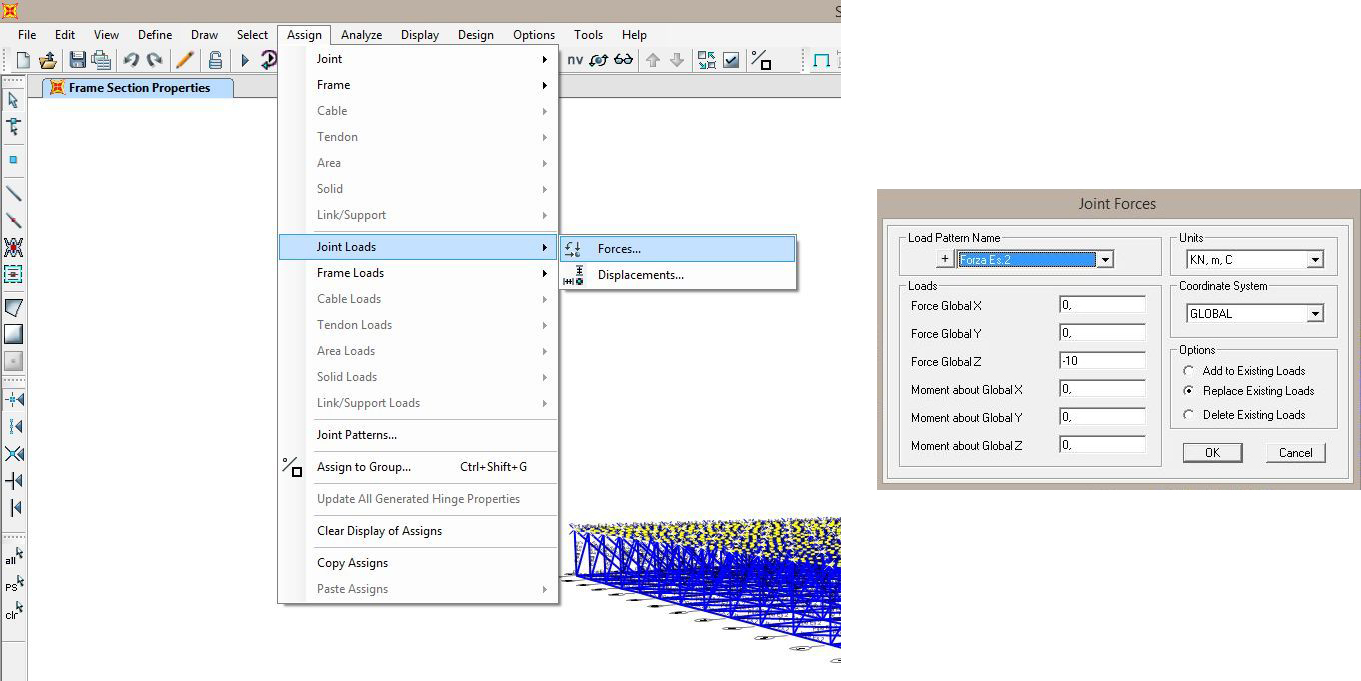
12. Assegnamo i carichi ai nodi che desideriamo (esclusivamente ai nodi dal momento che parliamo di una struttura reticolare) semplicemente selezionandoli e andando su Assign → Joint Loads → Forces... selezioniamo il tipo di carico da noi poc'anzi definito e definiamo il valore della forza (in questo caso una forza di -10kN lungo l'asse z avendo immaginato la struttura come una copertura)

Siamo finalmente pronti per lanciare l'analisi semplicemente cliccando sul simbolo play (►) e scegliendo di far partire il calcolo esclusivamente per il tipo di carico da noi creato (nel caso specifico Forza Es.2) e cliccando finalmente su Run Now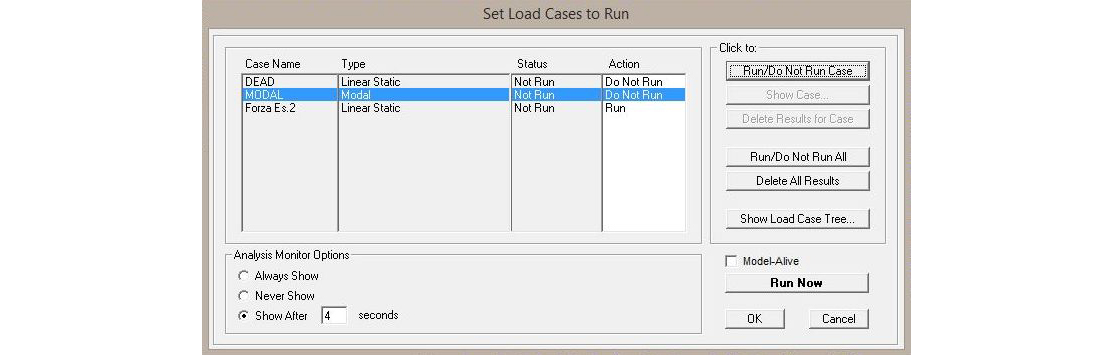

Terminata l'analisi, tra le varie proprietà che possiamo mettere in evidenza c'è la graficizzazione degli sforzi normali; clicchiamo sul pulsante Show Forces/Stresses quindi su Frames/Cables/Tendons... selezioniamo Axial Force. Possiamo inoltre impostare un fattore di scala o decidere se i diagrammi debbano essere campiti pieni o debbano mostrare anche il valore in cifre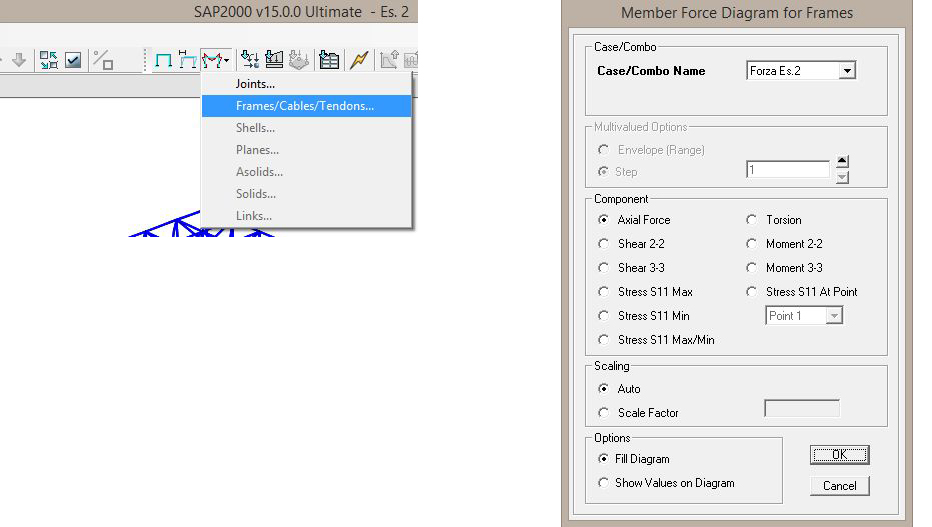

E questo è il grafico ottenuto; in blu è indicato lo sforzo di trazione (N+) ed in rosso lo sforzo di compressione (N-)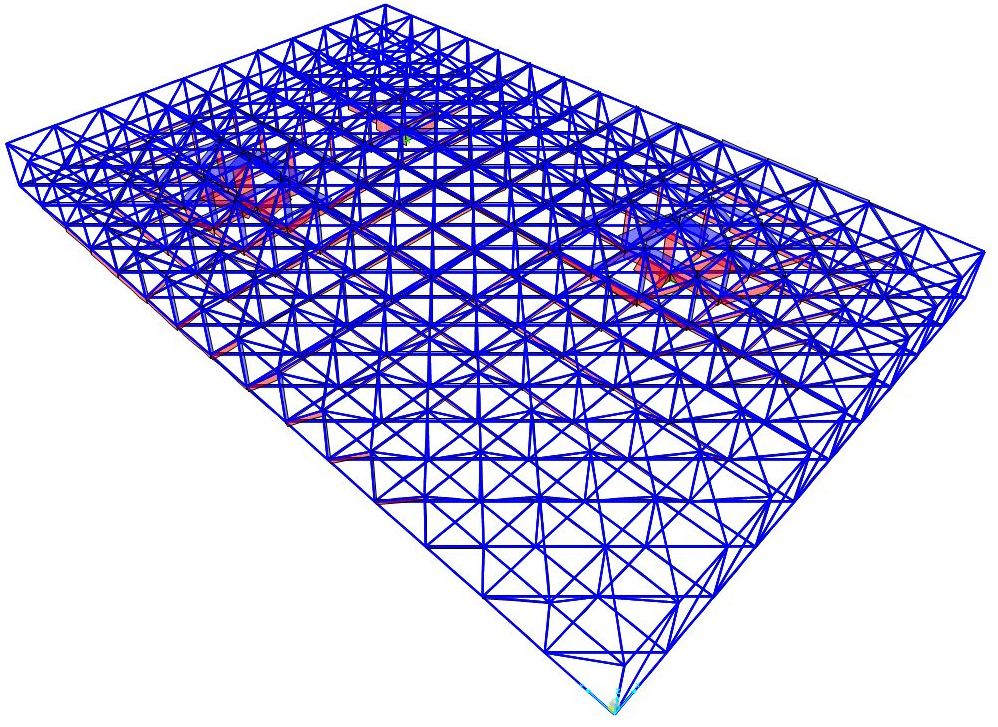

Per avere una lettura organica e chiara a questo punto è comodo costruirsi ed esportare una tabella nel quale viene indicato per ogni asta il valore dello sforzo normale (che è costante lungo tutta una qualsiasi asta della struttura). Andiamo su Display → Show Tables... e spuntiamo la casella ANALYSIS RESULTS e diamo quindi l'ok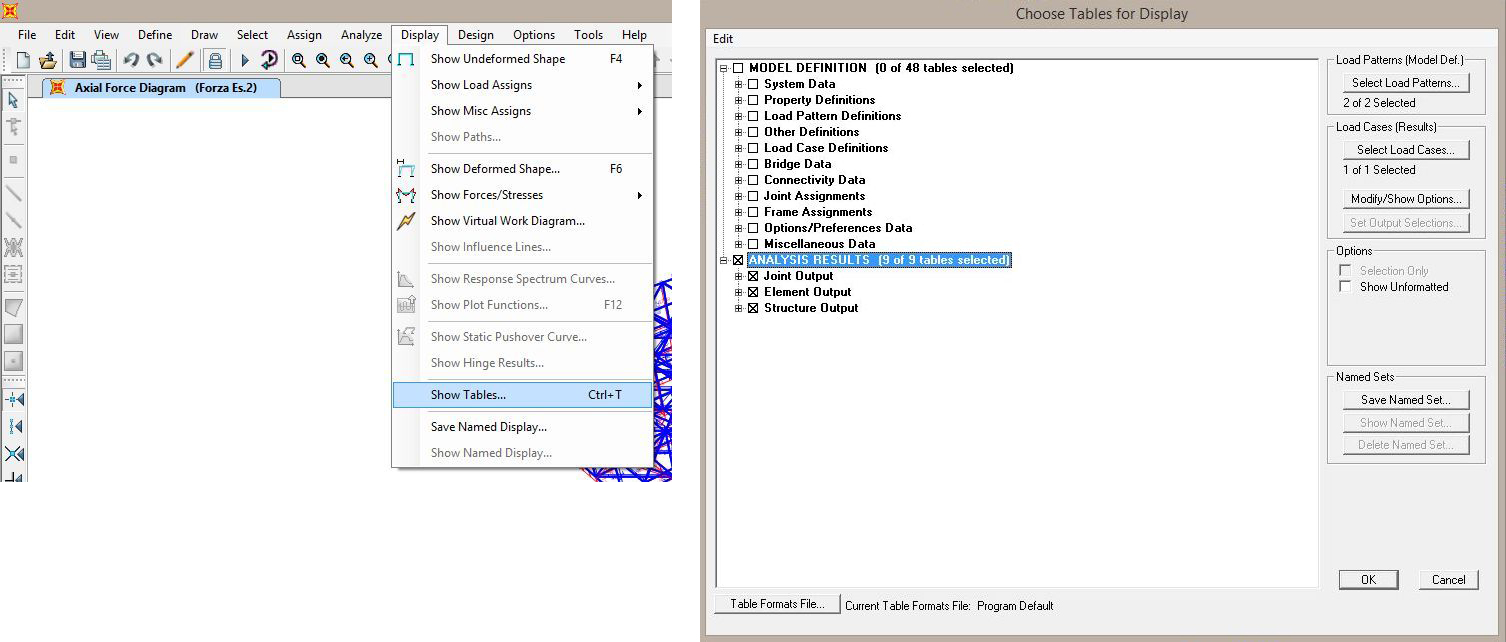

A questo punto dal menu a tendina selezioniamo Element Forces - Frames

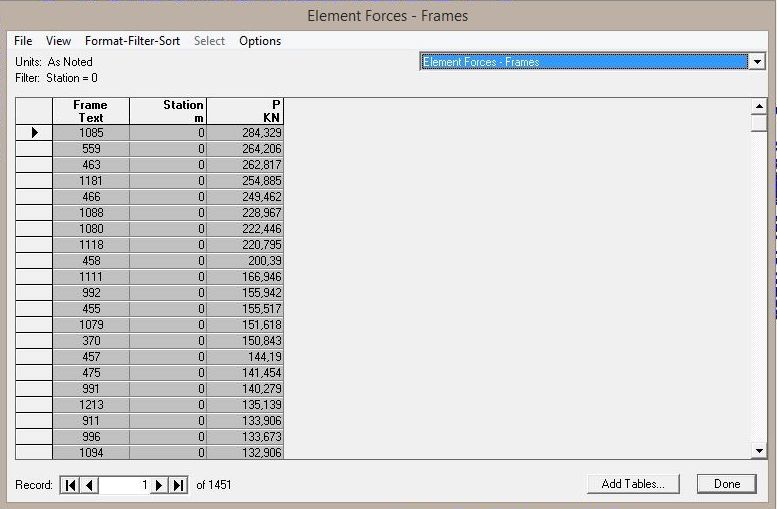
Giocando con le seguenti opzioni ho creato la mia tabella:

• Format: ho deciso quali colonne stampare  e quali no. Ho scelto di stampare le colonne Frame ('Asta'; ciascuna asta è indicata da un numero), Station (punto dell'asta dove è calcolato lo sforzo normale rispetto alle coordinate locali dell'asta) e P (lo sforzo normale espresso in KN)
• Filter: dal momento che, come precedentemente detto, lo sforzo normale è costante lungo tutta l'asta per qualsiasi asta, ho scelto di filtrare la colonna Station solo per i valori = 0 (in questo modo ogni asta compare nella tabella una sola volta)
• Sort: ho deciso di ordinare la tabella per valori decrescenti dello sforzo normale

Siamo ora pronti per esportare la tabella in Excel cliccando dal menù della tabella su File → Export Current Table → To Excel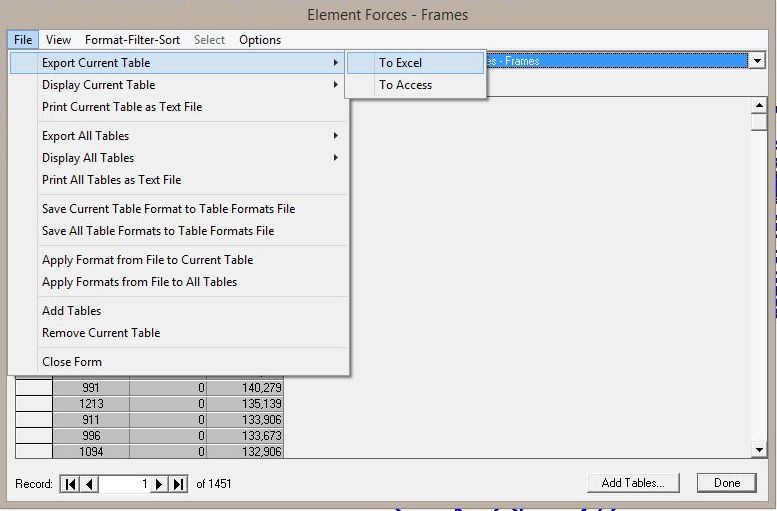 

Da Excel possiamo rapidamente mettere a confronto i valori massimi di trazione e compressione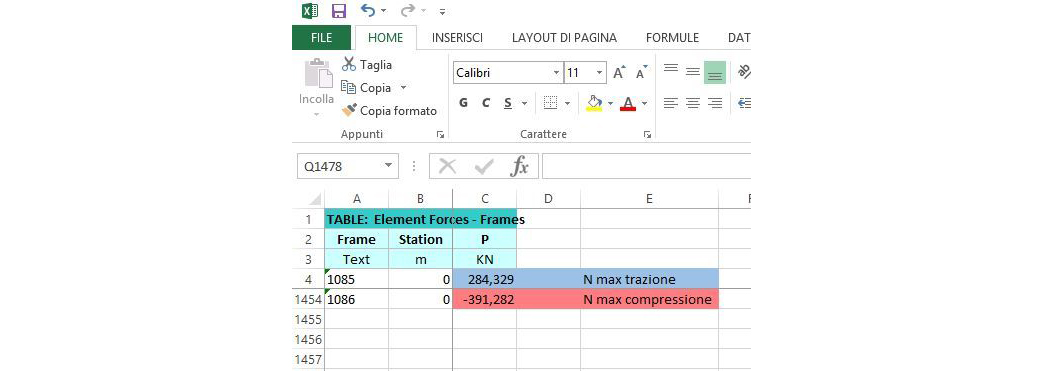

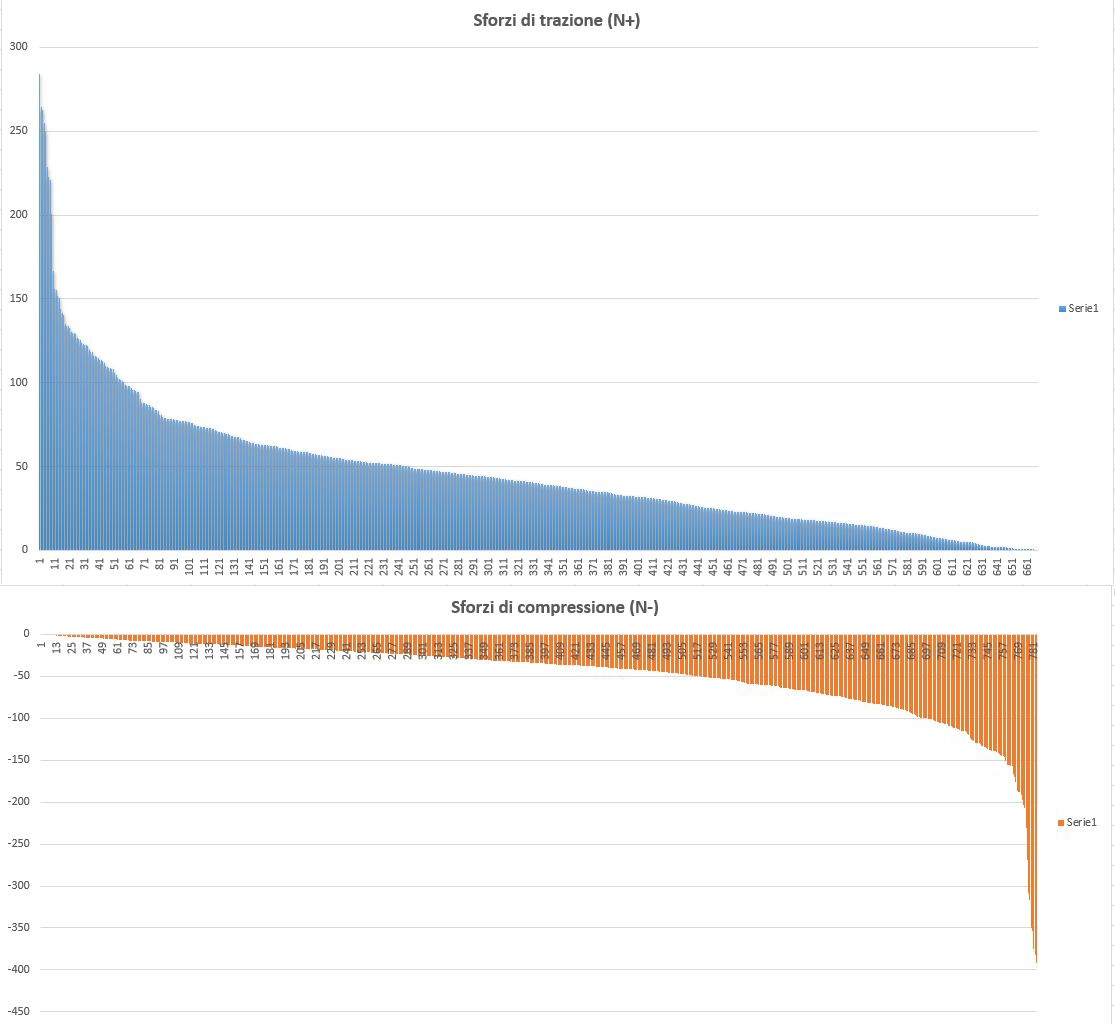
Inoltre graficizzando tutti i valori di N appare chiaro che:

• solamente il 2.1% delle aste tese supera il valore di N=150KN
• solamente il 1.3% delle aste compresse supera il valore di N=|150|KN
• il 63.2% delle aste tese subisce una trazione > 50kN
• il 65.9% delle aste compresse subisce una compressione > |50|kN
• il 34.7% delle aste tese subisce una trazione 150kN > N > 50kN
• il 32.8% delle aste compresse subisce una compressione |150|kN > N > |50|kN

Ora possiamo passare al dimensionamento delle aste:

• Aste tese
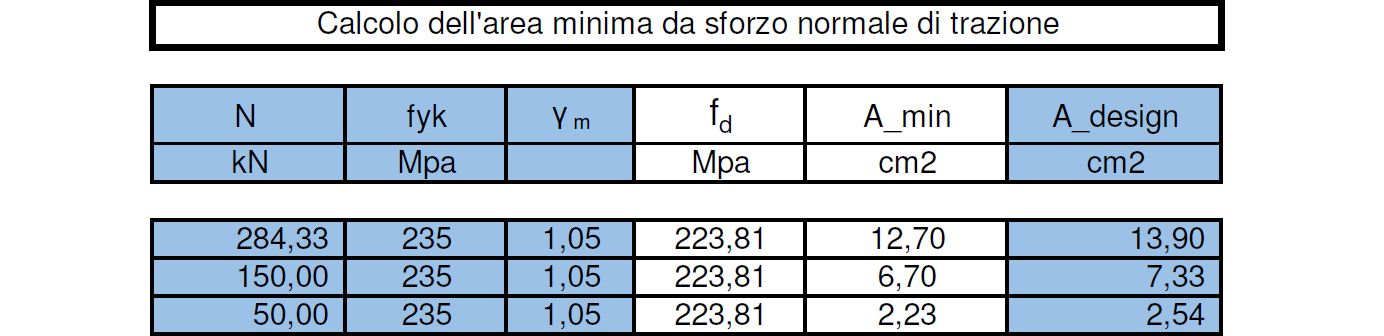
  Poiché σ = N/A, A = N/σ dove σ equivale in fase di progetto a f_d.
  con:
  • N = rispettivamente Nmax (284.329kN); 150kN; 50kN

  • f_yk = tensione di snervamento caratteristica dell’acciaio scelto espressa in MPa

  • γ_m= coefficiente di sicurezza adimensionale

  • f_d = tensione di progetto il cui valore è dato da f_yk / γ_m

  • A_min = area minima ricavata dal rapporto tra la sollecitazione N e la tensione di progetto f_d

  • A_design = Area ingegnerizzata, cioè l'area del profilo scelto da profilario subito maggiore dell’area minima e quindi a favore di sicurezza.​

• Aste compresse
  Per dimensionare le aste compresse abbiamo bisogno di altri parametri, in quanto dobbiamo tener conto dell'instabilità euleriana. 
  Poiché il carico critico euleriano è:
  f_crit=(π²EA) / λ² 
  allora
  σ_crit=(π²E) / λ²
  e quindi 
  λ_max=π(E/σ_crit)^1/2
  e poiché 
  λ=l₀/rho dove 
  l₀=beta(l)=luce libera d'inflessione con beta=1 per un'asta incernierata alle due estremità
  allora 
  rho_min=l₀/λ_max 
  e poiché 
  rho_min=(I_min/A)^1/2
  allora 
  I_min=A(rho_min)²
  - nella tabella ho assunto σ_crit=f_yd non fidandomi della fase duttile dell'acciaio
  - per l ho preso il valore della luce delle aste più lunghe, cioè quelle diagonali, pari a 2,83m (quelle parallele agli assi del sistema di riferimento hanno invece l=2m)

  Determinati per ciascun carico (determinato come sopra spiegato attraverso la distribuzione delle intensità di sforzo normale) i valori di λ_min, rho_min e I_min, ho trovato nel profilario il profilo che soddisfaceva i tre parametri e li ho inseriti nelle ultime tre colonne rosse verificando che il valore λ risultante dall'ultima colonna fosse <200 (valore massimo della snellezza da normativa per le membrature principali)