Verifica a deformabilità di una trave a sbalzo

Prendendo in considerazione i dati calcolati nella precedente esercitazione (carichi del solai) , vado a ricavarmi l'altezza minima della trave per quanto riguarda il cemento armato ed il legno e la resistenza a flessione minima per l'acciaio. Dovendo progettare una trave a sbalzo l'unica differenza di calcolo che si può riscontrare rispetto alla precedente esercitazione è  nella formula del momento massimo , non più ql^2/8 ma  ql^2/2 poichè il sistema equivale a quello di una mensola. Dopo aver progettato la sezione della mia trave in tutte le tecnologie, per questo sistema statico si considera  un altro fattore: LA DEFORMABILITA'. La verifica a deformabilità  si basa sul rapporto della luce della mia trave (sbalzo) e l'abbassamento massimo, che deve essere >250. Essa non viene effettuata allo SLU (stato limite ultimo -collasso), ma allo SLE (stato limite di esercizio-funzionalità ed efficienza).

Inizio la mia esercitazione con la carpenteria che sarà uguale per tutte le mie strutture. La trave evidenziata in rosso è la trave più sollecitata. La luce sarà di 3m e l'interasse di 5m. Per cui la mia area d'influenza sarà di 3mx5m = 15mq  

CEMENTO ARMATO :

qs = 2,46 KN/mq                      qp =  3,1 KN/mq                  qa = 2 KN/mq

Si andrà a calcolare il carico ultimo (qu) sommando tutti i carichi (strutturali, permanenti e accidentali) moltiplicati per i propri coefficienti di sicurezza ed infine moltiplicati per l'interasse.

                               qu =   (  qs x 1,3 + qp x 1,5 + qa x 1,5 ) x 5 =  54,34 KN/m

Momento max = 244,08 KNm

Ipotizzo la base della mia trave pari a 40 cm e risulta un altezza minima di 50,77cm che andrò ad ingegnerizzare portandola ad un altezza ultima di 55cm. La sezione della trave sarà di 40cmx55cm ed è VERIFICATA  considerando naturalmente anche il peso proprio della trave progettata con un Fyk = 450Mpa e Fck di 30Mpa.

Deformabilità:

 Il peso proprio della trave utilizzato precedentemente per la progettazione della sezione allo SLU, adesso viene riutilizzato per trovare il qe= carico totale allo SLE. Il carico totale qe=38,30KN/mq, il modulo elastico E=210000Mpa ed il momento d'inerzia Ix=55453 cm^4 mi permettono di trovare l'abbassamento massimo vmax=0,33cm Se il rapporto tra la L(luce)/vmax > 250 allora l' abbassamento massimo della mia trave a sbalzo è verificato. Nella mia esercitazione ottengo un L/vmax = 900,98 > 250 VERIFICATO.

LEGNO:

qs = 0,36 KN/mq                      qp =  3,34 KN/mq                  qa = 2 KN/mq

Si andrà a calcolare il carico ultimo (qu) sommando tutti i carichi (strutturali, permanenti e accidentali) moltiplicati per i propri coefficienti di sicurezza ed infine moltiplicati per l'interasse.

                                qu =   (  qs x 1,3 + qp x 1,5 + qa x 1,5 ) x 5   =  42,39KN/mq

Momento max = 190,775 KNm

Ipotizzo la base della mia trave pari a 35 cm e risulta un altezza minima di 58,60cm che andrò ad ingegnerizzare portandola ad un altezza ultima di 60cm. La sezione della trave sarà di 35cmx60cm

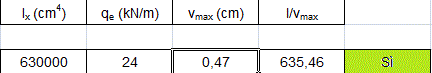
Deformabilità:

Nella fase di progetto della sezione per quanto riguarda il legno, essendo un materiale leggero,il peso proprio della trave progettata viene trascurato, quindi, nella formula per trovarci qe( il carico totale allo SLE) ,non viene sommato. Il carico totale allo SLE qe=24KN/mq, il modulo elastico E=8000Mpa e il valore del momento d'inerzia Ix=630000cm^4 (b*h^3/8) mi permettono di trovare l'abbassamento massimo vmax=0,47cm .Se il rapporto tra la L(luce)/vmax > 250 allora l' abbassamento massimo della mia trave a sbalzo è verificato. Nella mia esercitazione ottengo un L/vmax = 635,46 > 250 VERIFICATO

ACCIAIO:

qs = 2,12 KN/mq                      qp =  2,98 KN/mq                  qa = 2 KN/mq

                                     qu =   (  qs x 1,3 + qp x 1,5 + qa x 1,5 ) x 5   = 51,13 KN/mq

Momento max = 230,085 KNm

Scegliendo l'acciaio Fe 430/S275 che avrà una tensione di snervamento pari a 275Mpa otterrò un modulo di resistenza Wxmin pari a 878,51 cmc che equivale ad un IPE 360 perchè considero un Wx pari a 904cmc.

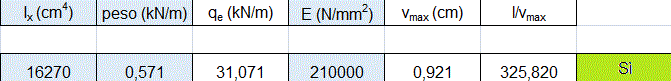
Deformabilità:

Prendendo quindi in considerazione un IPE 360 avrò il peso della trave pari a 0,571 KN/m (che verrà sommato ai carichi del solaio ), un momento d'inerzia Ix=16270 cm^4 ed un modulo elastico E=210000Mpa. Tutti questi dati mi permettono di trovare l'abbassamento massimo della mia trave a sbalzo pari a  vmax=0,921cm. Se il rapporto tra la L(luce)/vmax > 250 allora l' abbassamento massimo della mia trave a sbalzo è verificato. Nella mia esercitazione ottengo un L/vmax = 325,820 > 250 VERIFICATO.