III ESERCITAZIONE – VERIFICA A DEFORMABILITA ’ DI UNO SBALZO (MENSOLA) – C.A., Acciaio, Legno

DIMENSIONAMENTO DI UNA TRAVE A SBALZO

Questa esercitazione si divide in due fasi: nella prima vado a dimensionare la sezione di una trave nelle 3 tecnologie, esercizio svolto in precedenza, considerando nei calcoli i coefficienti riguardanti lo stato limite ultimo (SLU). Nella seconda fase andrò a verificare la deformabilità della trave a sbalzo sempre in cemento armato, acciaio e legno considerando invece in questo caso i coefficienti che riguardano lo stato limite d’esercizio (SLE ). Questi coefficienti di sicurezza sono dettati entrambe dalla normativa vigente.

Riporto la pianta di carpenteria di un solaio di un edificio residenziale, individuandone la trave più sollecitata

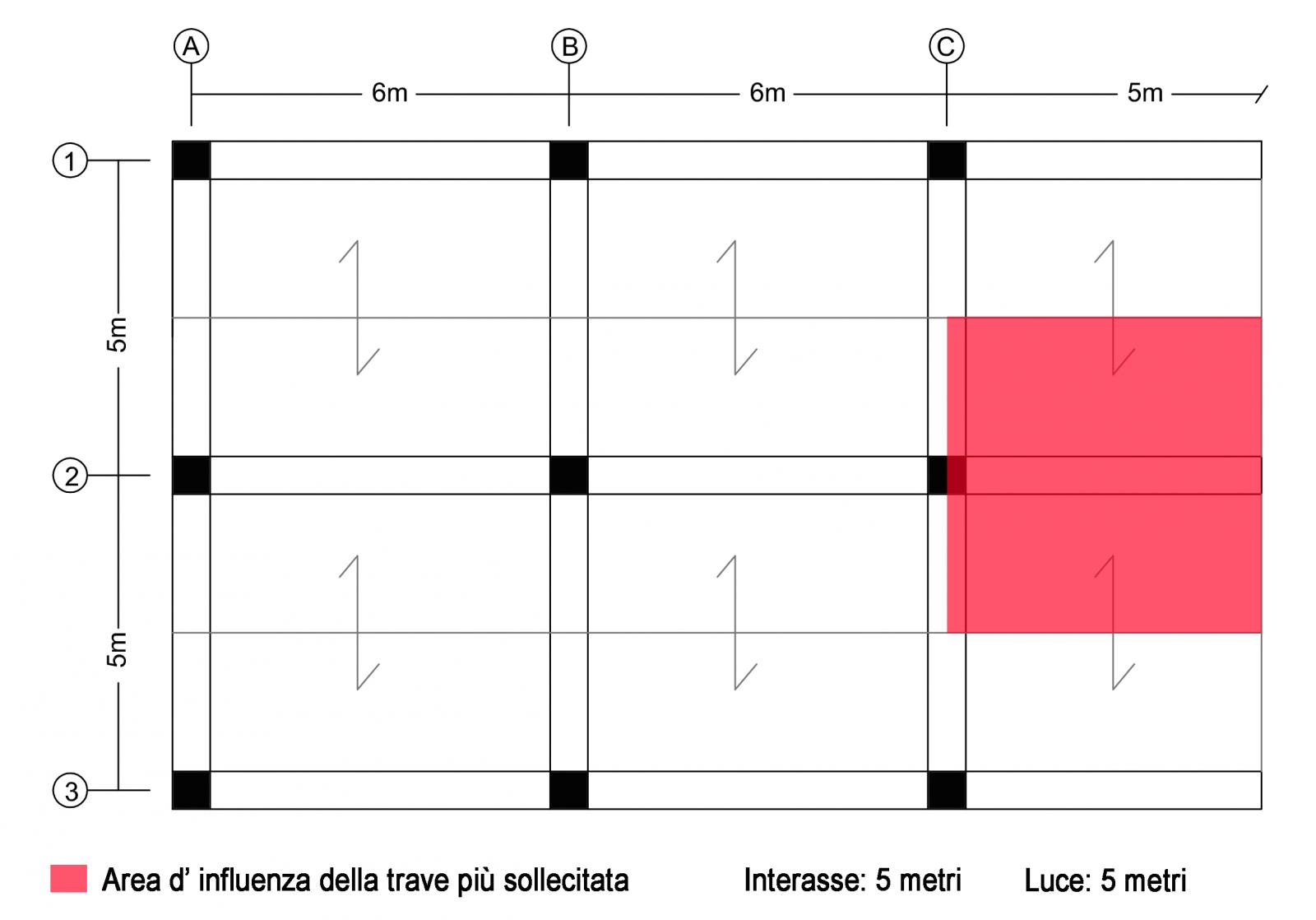
Per tutti e tre i casi di tecnologie prese in esame:

•  il modello statico a cui si fa riferimento è una mensola incastrata in una estremità., il cui Momento massimo in corrispondenza della sezione d' incastro è : qL²/2

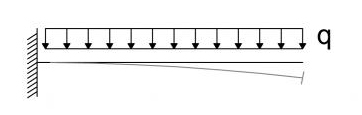
• Il fine ultimo della mia esercitazione è verificare che la deformabilità della trave a sbalzo sia inferiore a 1/250 della sua luce, come da normativa per i solai.
• Il procedimento si effettua allo SLE in modo tale che spostamenti e deformazioni non limitino l’uso e l’efficienza della costruzione.
• Si considerino  come carichi strutturali , permanenti e accidentali i valori della prima esercitazione che riporterò sinteticamente.

CEMENTO ARMATO                                                                                                                               Stratigrafia di un generico solaio misto in latero-cemento. Prendo in esame un metro quadro (m²) di solaio:

Calcolo il peso di ogni singolo elemento del solaio  al metro quadro: moltiplico il suo peso specifico in kN/m³ per il suo stesso volume e lo divido per  un metro quadrato.

Per gli altri dati di progetto della sezione della trave faccio riferimento alla prima esercitazione, fatta eccezione per fck che è la resistenza caratteristica a compressione del calcestruzzo data dal tipo di cls scelto,  in questo caso scelgo un cls  meno performante con un a resistenza pari a 30 N/mm².

Imposto poi la base della mia trave a 50 cm e dalla tabella excel mi viene fuori un altezza min di 71,06 cm che Ingegnerizzo a 80cm. Nella seconda riga della tabella viene aggiunto al carico unitario Qu il peso unitario della mia trave, avendo il cemento armato un peso specifico molto significativo, e scopro così che la mia trave 50x80 è VERIFICATA. 

Ora passo alla seconda fase dell’ esercitazione in cui verifico la deformabilità dello sbalzo.

Mi calcolo il Qe, ossia il carico di esercizio:  sommo i carichi  permanenti, li addiziono a Qa che moltiplica 0.5 (un coefficiente di sicurezza per quanto riguarda SLE), moltiplico tutto per l’interasse (5m) e infine lo sommo peso prorpio della trave.

Inserisco infine altri due dati quali E , il modulo di elasticità del cemento,  e I_x , ossia il momento di inerzia che viene ricavato dalla formula bh³/12.

Ora che ho tutti i miei dati posso calcolarmi l’ ABBASSAMENTO della mia trave a sbalzo:

V_max=  q_e l^4//8EI_x  = 0.70

Q è il il carico d’esercizio, direttamente proporzionale allo spostamento

L è la luce che è direttamente proporzionale all’ abbassamento alla quarta potenza, quindi influisce molto

E è il modulo di elasticità che è inversamente proporzionale all’ abbassamento

I è  il momento di inerzia della sezione inversamente proporzionale allo spostamento, dunque più aumenterò l’altezza della sezione più l’inerzia sarà maggiore e più la trave faticherà ad inflettersi

Ora è necessario verificare che il rapporto l/ v_max   sia ≥ 250.

In questo caso il rapporto l/ v_max = 709,79 perciò questo abbassamento è accettato dalla struttura, di conseguenza lo sbalzo è realizzabile.

LEGNO

Prendo in analisi un metro quadro (m²) di un solaio di una struttura in legno rappresentato in sezione:

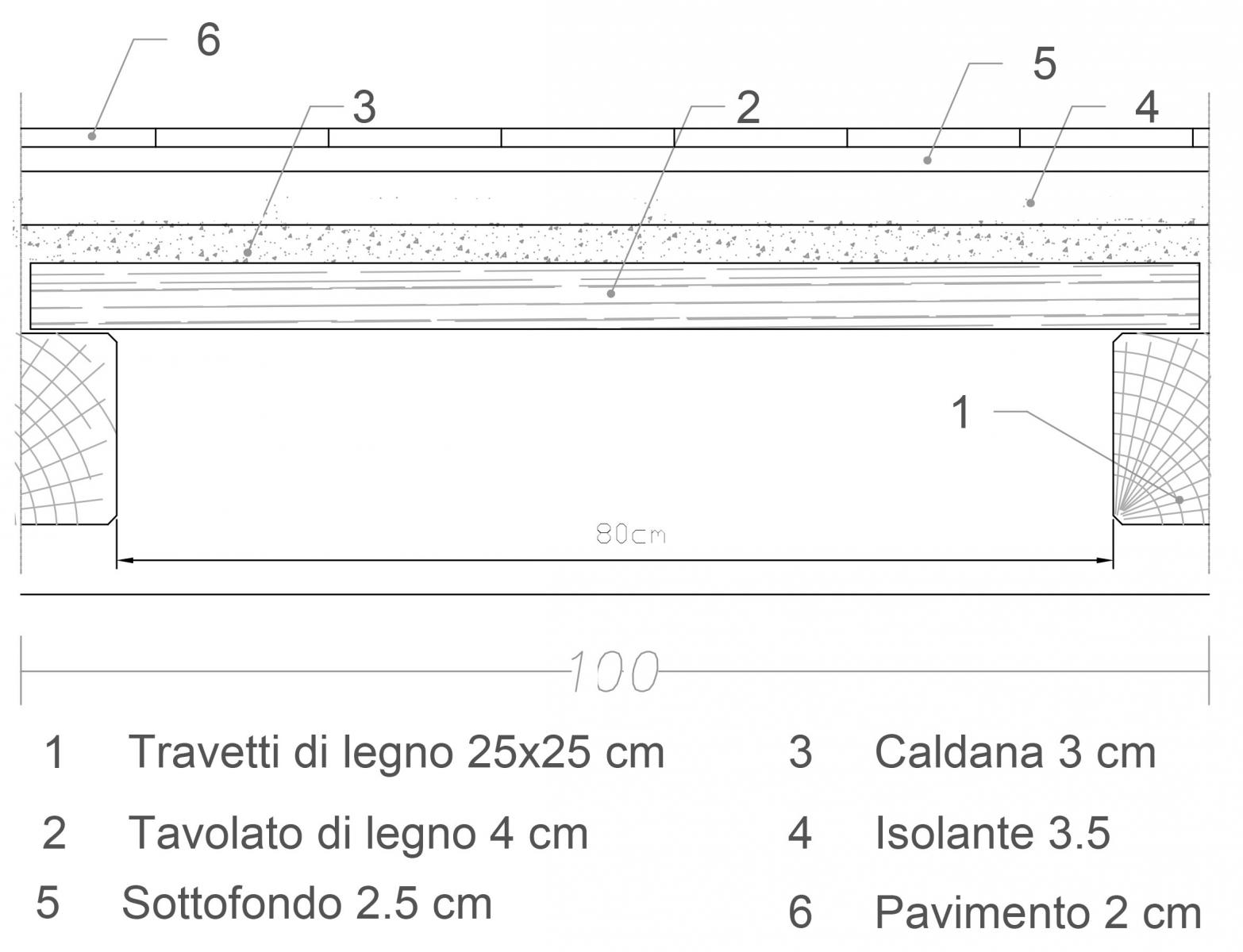
 Scelgo di utilizzare un legno lamellare incollato GL28h.

Calcolo il peso di ogni singolo elemento del solaio  al metro quadro: moltiplico il suo peso specifico in kN/m³ per il suo stesso volume e lo divido per  un metro quadrato.                

 A questo punto posso  calcolarmi il momento massimo M agente sulla trave avendo il carico lineare qu.

Ipotizzo una base di 35 cm e dal foglio di calcolo trovo l’altezza minima della trave di legno. L’altezza minima viene 70 cm e con una  ingienierizzazzione arrivo ad un’ altezza 75cm.

Inserico anche qui due informazioni fondamentali per calcolare lo spostamento, quali E che nel legno è pari a 126.000 N7mm² e il foglio mi calcola I_x la cui formula essenzo una sezione di trave rettangolare è sempre bh³/12.

Ricalcoliamo ora i carichi incidenti sulla struttura seguendo come abbiamo fatto per il C.A. la combinazione impiegata per gli stati limite di esercizio , solo che in questo caso, dunque solo nel LEGNO, il peso proprio della trave viene trascurato essendo un materiale leggero.

Posso calcolarmi a questo punto l’ abbassamento della mia trave a sbalzo.

L’abbassamento totale è calcolabile attraverso questa formula , in quanto il carico è uniformemente distrubito :

V_max=  q_e l^4//8EI_x  = 0.11 cm

A livello dimensionale:

[v_max] ₌ [F] [L³]/ [F] [L^-2] [L⁴] = [L]

Verifichiamo infine che l’abbassamento sia accettabile, a tal proposito la normativa impone che la luce fratto lo spostamento sia maggiore uguale di 250:  trasformo la luce di 5 m in 500 cm e la divido per l’abbassamento di 0.11 cm =  4669,41   VERIFICATO

ACCIAIO

Prendo in analisi un metro quadro (m²) di un solaio di una struttura in acciaio così stratigrafata:

Calcolo il peso di ogni singolo elemento del solaio  al metro quadro: moltiplico il suo peso specifico in kN/m³ per il suo stesso volume e lo divido per  un metro quadrato.

Dopo di che come fatto per il c.a. e il legno mi calcolo il Momento massimo, inserisco l’ Fyk cioè la tensione di snervamento che nel mio caso avendo scelto un acciaio medio S275 è di  275 Nmm² e mi calcolo così la tensione di progetto fd  ( tensione ammissibile) dividendo fyk per un il coefficienti di sicurezza per la resistenza delle membrature e la stabilità,  γs = 1,05 :

Fd = 275/1.05= 261.90