Esercitazione IV - Dimensionamento pilastro in calcestruzzo, legno ed acciaio

                              

Lo scopo di quest’esercitazione è quello di dimensionare un elemento soggetto a sforzo normale centrato di compressione, dove la deformazione Δl < 0 viene definita contrazione. In questo caso è necessario considerare, oltre alla rottura del materiale, anche il fenomeno di instabilità euleriana.  A tal fine sarà fondamentale definire due grandezze: l’area e il momento d’inerzia minimo della sezione.

L’area minima che deve essere ricavata, in modo da evitare lo schiacciamento del materiale, si ottiene eguagliando la tensione massima sulla sezione (σ_max) alla resistenza di progetto del materiale (f_cd).

σ_max = f_cd

σ_max = N / A_min

quindi:

N/A_min = f_cd

A_min = N / f_cd

Il momento di inerzia minimo della sezione si ottiene eguagliando la tensione massima sulla sezione (σ_max) alla tensione critica (σ_crit) generata del carico critico euleriano ovvero la forza di compressione che innesca il fenomeno di instabilità.

Per ricavare la tensione critica è dunque necessario definire il carico critico euleriano (N_crit).

N_crit= π² x E x I_min / (β x L)²

Dove:

E = modulo di elasticità del materiale

I_min= il minore momento di inerzia tra I_x e I_y

β = coeff. adimensionale relativo al tipo di vincolo (nella figura sottostante)

L = lunghezza dell’elemento

Attraverso le seguenti relazioni si giunge alla definizione di carico critico euleriano:

I_min = A x ρ_min²

λ = L₀ x ρ_min

dove L₀ è la luce libera di inflessione ed è pari a βL

N_crit = π² x E x A / λ²

σ_crit = N_crit / A = π² x E / λ²

Essendo l’instabilità un fenomeno impossibile da controllare e dovendo mettere in relazione la σ_crit con la σ_max (ricordando che σ_max = f_cd), si impone f_cd < σ_max in modo tale che la tensione raggiunga per prima la resistenza schiacciamento del materiale, con conseguente rottura.

 

Dimensionamento pilastro in calcestruzzo

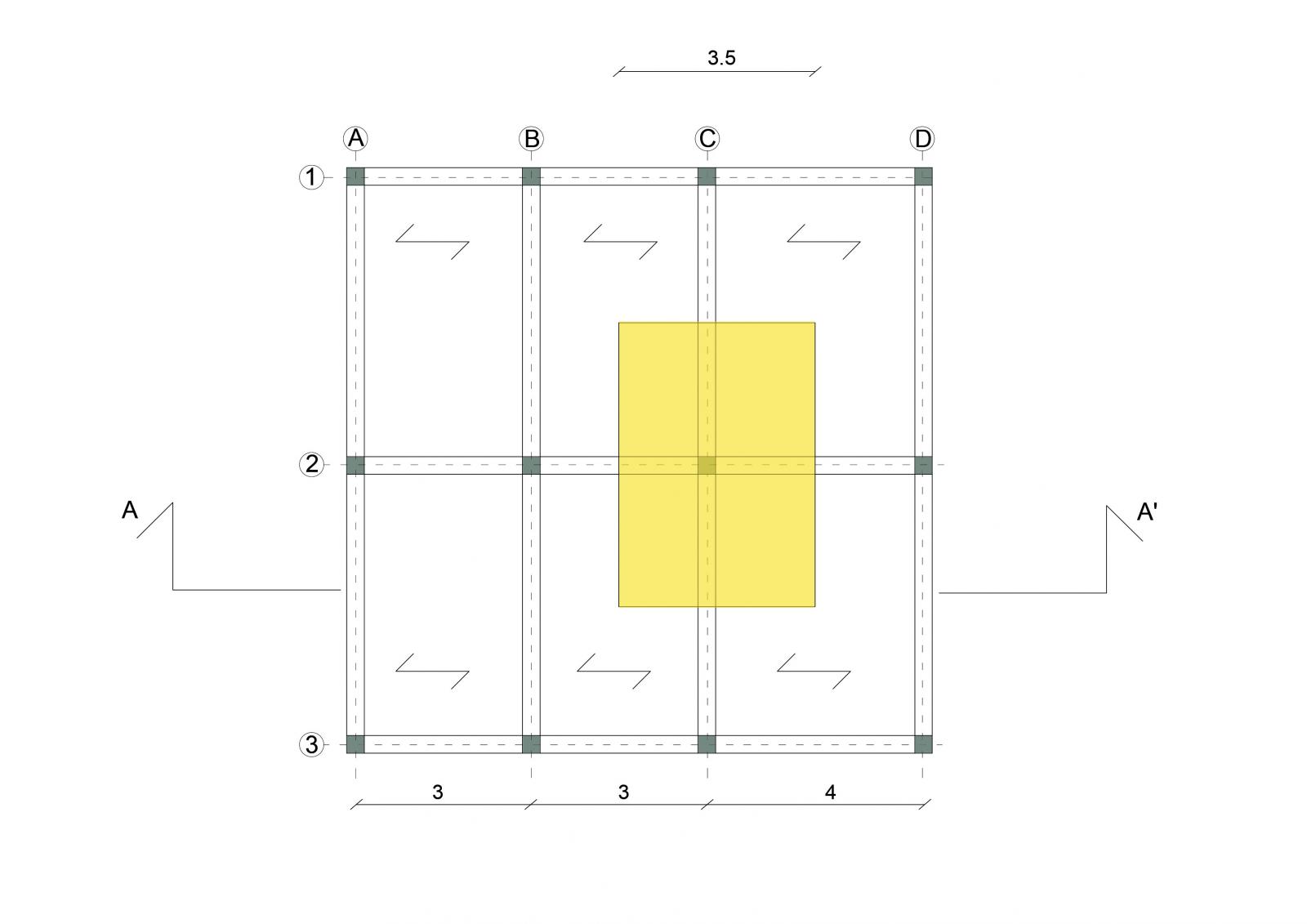
Prima di tutto viene individuata l’area di influenza del pilastro.

Area = L₁ x L₂

Il secondo passo è quello di individuare lo sforzo normale di compressione. A tal fine è indispensabile calcolare il carico dovuto al peso delle travi sul pilastro, il carico del solaio ed il numero dei piani dell’edificio.

 

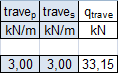
Carico del peso delle travi sul pilastro

Peso proprio delle travi [KN/m] = Area [m²] x Peso specifico [KN/m³]

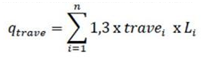
Area_p = (0,3*0,4) [m²] *25 [KN/m] = 3 [KN/m]

Area_s = (0,3*0,4) [m²] *25 [KN/m] = 3 [KN/m]

Quindi,

q_trave = 3*1,3*5 + 3*1,3*3,5 = 33,15 [KN]

Carico del solaio

I carichi strutturali, permanenti ed accidentali del solaio sono stati recuperati dalla prima esercitazione per individuare il carico totale del solaio sul pilastro, che si ricava dall’equazione di combinazione dei carichi (in questo caso sarà la combinazione dei carichi allo SLU).

Considerato che il numero dei piani dell’edificio è pari a 5, abbiamo ora tutti i valori necessari al calcolo di N:

N [KN] = (q_trave + q_trave) x n_piani

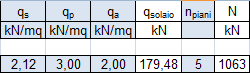
Si è scelta come classe di calcestruzzo C40/50 e, successivamente, è stata determinata la resistenza di progetto a compressione.

f_cd = f_ck / γ_m

Quindi è stata calcolata l’area minima e la base minima.

A_min = N / f_cd

b_min = √A_min

Inserendo il modulo di elasticità del calcestruzzo, il coefficiente di vincolo β e l’altezza dell’asta, si ottengono la snellezza, il raggio di inerzia minimo e la base minima.

λ_max = π x √(E / f_cd)

ρ_min = L₀ / λ_max

La base minima è calcolata come segue:

b_min = 2 x √(3 x ρ_min)

A questo punto la base minima deve essere opportunamente ingegnerizzata. Con l’area minima e la base minima si ottiene l’altezza minima, la quale va anch’essa ingegnerizzata opportunamente per calcolare infine l’area di design ed il momento di inerzia di design.

A_design = b x h

I_design = (b³ x h) / 12

Nel calcestruzzo è necessaria la verifica del pilastro a presso-flessione poiché, essendo il nodo trave-pilastro un incastro, trasmette momento. Per tale verifica si impone

σ_max ≤ f_cd

dove, σ_max è pari alla somma dello sforzo normale di compressione ed il momento trasmesso:

Lo sforzo normale di compressione è noto mentre il momento trasmesso viene calcolato come:

M_t = q_t x L_p² / 12

dove q_t rappresenta il carico distribuito sulla trave principale:

q_t = (1,3 x q_s + 1,5 x q_p + 1,5 x q_a ) x L_s

Il modulo di resistenza alla compressione è calcolato come segue:

W_max = b x h² / 6

Quindi per la verifica della sezione a presso-flessione si impone:

In questo caso risulta verificata.

 

Dimensionamento pilastro in legno

Viene individuata l’area di influenza del pilastro.

Area = L₁ x L₂

Carico del peso delle travi sul pilastro

Si calcola il peso delle travi principali e secondarie moltiplicandole per il loro peso specifico ed ottenendo il contributo totale del peso delle travi.

Peso proprio delle travi [KN/m] = Area [m²] x Peso specifico [KN/m³]

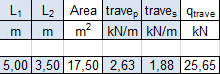
trave_p = (0,3*0,35) [m²] *25 [KN/m] = 2,63 [KN/m]

trave_s = (0,3*0,25) [m²] *25 [KN/m] = 1,88 [KN/m]

Quindi,

q_trave = 2,63*1,3*5 + 1,88*1,3*3,5 = 25,65 [KN]

 

Carico del solaio

I carichi strutturali, permanenti ed accidentali del solaio sono stati recuperati dalla prima esercitazione per individuare il carico totale del solaio sul pilastro, che si ricava dall’equazione di combinazione dei carichi (in questo caso sarà la combinazione dei carichi allo SLU).

Poiché il numero dei piani dell’edificio è pari a 5, abbiamo ora tutti i valori necessari al calcolo di N:

N [KN] = (q_trave + q_trave) x n_piani

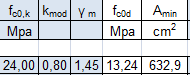
La resistenza a compressione si ottiene dopo aver scelto la classe di legno C24 con una f_ck = 24 MPa

f_cd = f_ck x k_mod / γ_m

dove k_mod è un coefficiente correttivo pari a 0,8 e γ_m è un coefficiente di sicurezza pari a 1,45. Quindi è stata calcolata l’area minima.

A_min = N / f_cd

Ora è necessario individuare il raggio di inerzia minimo che ci permetterà di ricavare la base minima che deve avere la sezione. Inserendo nel file Excel il modulo di elasticità E, il valore β e l’altezza del pilastro l, si ricava la snellezza massima ed il raggio di inerzia minimo.

λ_max = π x √(E / f_cd)

ρ_min = L₀ / λ_max

La base minima è calcolata come segue:

b_min = 2 x √(3 x ρ_min)

A questo punto la base minima deve essere opportunamente ingegnerizzata. Con l’area minima e la base minima si ottiene l’altezza minima, la quale va anch’essa ingegnerizzata opportunamente per calcolare infine l’area di design ed il momento di inerzia di design.

h = A_min / b

A_design = b x h

I_design = (b³ x h) / 12

 

 

Dimensionamento pilastro in acciaio

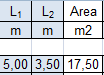
Viene individuata l’area di influenza del pilastro.

Area = L₁ x L₂

Carico del peso delle travi sul pilastro

Si calcola il peso delle travi principali e secondarie moltiplicandole per il loro peso specifico ed ottenendo il contributo totale del peso delle travi.

Peso proprio delle travi [KN/m] = Area [m²] x Peso specifico [KN/m³]

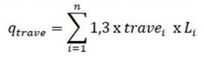
Per la trave principale si sceglie un IPE 270 CON PESO DI 36.1 Kg/m e, per la trave secondaria, un IPE 200 con peso di 22.4 kg/m.

trave_p = 0,36 [KN/m]*78,5 [KN/m] = 28,33 [KN/m]

trave_s =  0,22 [KN/m]*78,5 [KN/m] = 17,58 [KN/m]

Quindi,

q_trave = 28,33*1,3*5 + 17,58*1,3*3,5 = 264,04 [KN]

Carico del solaio

I carichi strutturali, permanenti ed accidentali del solaio sono stati recuperati dalla prima esercitazione per individuare il carico totale del solaio sul pilastro, che si ricava dall’equazione di combinazione dei carichi (in questo caso sarà la combinazione dei carichi allo SLU).

Poiché il numero dei piani dell’edificio è pari a 5, abbiamo ora tutti i valori necessari al calcolo di N:

N [KN] = (q_trave + q_trave) x n_piani

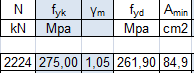
La resistenza a compressione si ottiene dopo aver scelto la classe di acciaio S275 con una f_yk = 275 MPa

f_yd = f_yk / γ_m

dove γ_m è un coefficiente di sicurezza pari a 1,05. Quindi è stata calcolata l’area minima.

A_min = N / f_yd

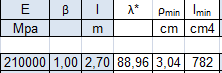
Ora è necessario individuare il raggio di inerzia minimo che ci permetterà di ricavare la base minima che deve avere la sezione. Inserendo nel file Excel il modulo di elasticità E, il valore β e l’altezza del pilastro l, si ricava la snellezza massima ed il raggio di inerzia minimo.

λ_max = π x √(E / f_yd)

ρ_min = L₀ / λ_max

A questo punto è necessario calcolare il momento di inerzia minimo:

I_min = A x ρ²_min

Conoscendo I_min si può scegliere la sezione del pilastro sul formulario, verificando che:

• L’area di design sia maggiore/uguale rispetto a quella trovata
• Il momento di inerzia sia maggiore/uguale rispetto a quello trovato
• Il raggio di inerzia sia maggiore/uguale rispetto a quello trovato

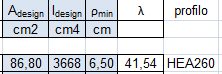
Quindi viene individuata la sezione del pilastro HEA260, con le seguenti misure:

A_design = 86,80 > 84,9 [cm²]

I_design = 3668 > 782 [cm⁴]

ρ_design = 6,50 > 3,04 [cm]