ESERCITAZIONE 4 _ Dimensionamento di un pilastro (in legno. acciaio e c.a.)

L'obiettivo dell'esercitazione è quello di dimensionare la sezione di un pilastro nelle tre tecnologie: legno, acciaio e cemento armato.

Si tratta di un pilastro soggetto a sforzo normale di compressione per cui nella progettazione bisogna tener conto anche dell'instabilità. Oltre a definire un'area minima per cautelarsi dalla rottura per schiacciamento (mettendo in relazione σ_max con fyd) definisco anche un momento d'inerzia minimo per evitare che si verifichi il fenomeno dell'instabilità, legato alla snellezza del pilastro (mettendo in relazione σ_max con σ_cr).

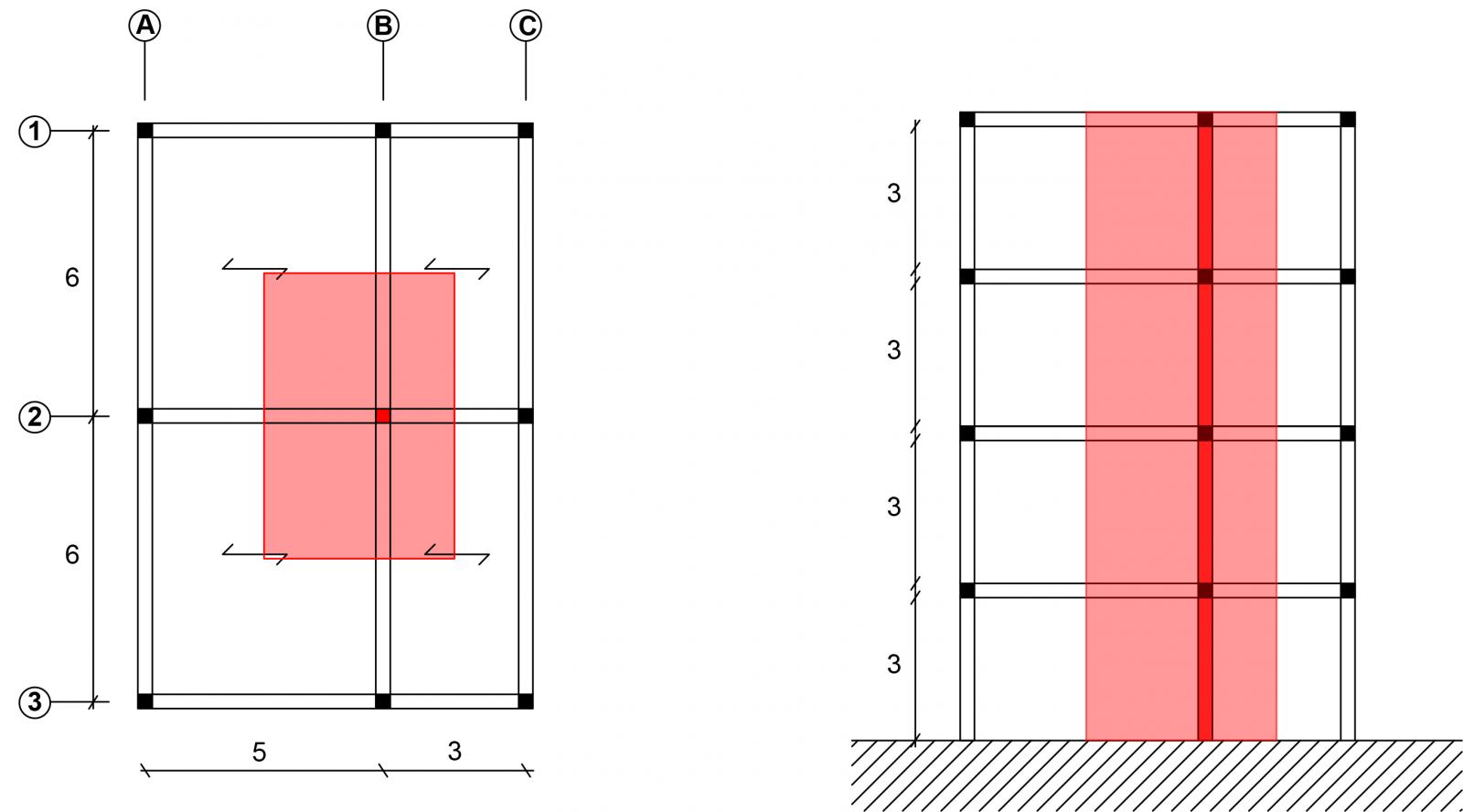
Prendo in considerazione un edificio di 4 piani di cui sono sotto riportati una pianta di carpenteria ed una sezione.   Sono evidenziati in rosso il pilasrto maggiormente sollecitato e la sua relativa area di influenza. Tra i pilastri di ogni piano, quello a piano terra sarà più sollecitato rispetto agli altri.

LEGNO:

Nel file excel calcolo per prima cosa l'area di influenza del pilastro (L₁ x L₂) , poi il carico del solaio e quello delle travi, per ottenere lo sforzo totale di compressione N sul pilastro [(q_trave + q_solaio) x n.piani].

Il carico del solaio, dato dai carichi strutturale, permanente e accidentale, è lo stesso delle esercitazioni precedenti; il carico delle travi è dato dal prodotto del peso proprio di ogni trave per la rispettiva lunghezza contenuta nell'area d'influenza.

Inserisco poi nel foglio di calcolo le informazioni relative alla resistenza del materiale (legno strutturale C24) e, dividendo N per f_c0d , ottengo l'area minima per evitare la crisi per schiacciamento.

A questo punto devo calcolare il momento d'inerzia minimo della sezione per evitare che si verifichi il fenomeno dell'instabilità. Qesto è legato alla snellezza (λ) del pilastro, cioè al rapporto tra la sua "altezza" e la sua "larghezza" ossia alla lunghezza libera di inflessione (l₀) diviso il raggio giratore di inerzia (ρ); per questo maggiore è l'inerzia della sezione, minore è λ e minore è il rischio che si verifichi il fenomeno dell'instabilità.

Inseriti i valori del modulo di elasticità (E), di β (legato ai vincoli a cui è soggetto il pilastro analizzato), e dell'altezza del pilastro (l) ricavo quindi il raggio di inerzia minimo che, in casi come questo di sezioni rettangolari, permette di ricavare la base della sezione (piochè ρ_min=√1/12b).

Avendo la base posso ricavare anche un'altezza minima; ingegnerizzo entrambi i valori ed ottengo l'area della mia sezione che dovrò confrontare con l'area minima ricavata all'inizio: la sezione risulterà verificata se, e solo se, A_design > A_min

ACCIAIO:

Anche per il pilastro in acciaio, dopo aver ricavato l'area d'influenza, il carico delle travi e quello del solaio, ottengo lo sforzo di compressione N.

Inserisco i valori di resistenza dell'acciaio (S235) ed ottengo l'area minima per evitare la rottura.

Inserisco poi i valori del modulo di elasticità (E), dell'altezza del pilastro (l) e di β (β  = 1 anche in questo caso perchè ci troviamo in presenza di un nodo di tipo "cerniera", quindi di una trave doppiamente appoggiata).  Ottengo così il momento d'inerzia minimo (Axρ²_min) che mi permette di scegliere un profilato dalla tabella delle HEA.

Nel mio caso una HEA140.

CEMENTO ARMATO:

Anche in questo caso calcolo l'area di influenza del pilastro, il carico delle travi e quello del solaio per ricavare lo sforzo di compressione N.

Inserisco la tensione di resistenza caratteristica f_ck da cui ottengo quella di progetto f_cd e da N/f_cd ricavo un'area minima per la sezione del pilastro.

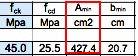
Inserisco poi i valori del modulo di elasticità (E), di β e dell'altezza del pilastro (l) per trovare una base minima e di conseguenza un'altezza minima.

Il β in questo caso sarà 0,5 poichè siamo in presenza di un nodo di tipo "incastro";per questo motivo il momento a cui la trave è soggetta si trasferisce sul pilastro che dovrò quindi verificare a presso-flessione.

Devo quindi ingegnerizzare base e altezza minime in modo da verificare la condizione: σ_max≤f_cd .