blog di silvia parentini

L'esercitazione consiste nel calcolare su un impalcato la ripartizione di forze orizzontali (che simulano le azioni del vento o del sisma). Per farlo utilizziamo il metodo delle rigidezze. 

L'impalcato in questione è composto da 7 telai shear-type in cemento armato: 4 verticali (1-5, 2-6, 3-7-9, 4-8-10) e 3 orizzontali (1-2-3-4, 5-6-7-8, 9-10).

Rappresentiamo i controventi con delle molle dal momento che sono dei vincoli cedevoli elasticamente, rappresentano cioè le forze che i telai oppongono quando l'impalcato viene spostato. 

Per calcolare la rigidezza di ogni telaio usiamo il foglio Excel dove inseriamo i dati relativi ai pilastri che lo costituiscono. Si tratta in questo caso di pilastri di sezione 30x40cm con momento d'inerzia minore pari a 90000cm⁴ e momento di inerzia maggiore 160000 cm⁴.

La rigidezza dei pilastri del telaio shear type è data dalla formula: K=12EI/h³. Nei casi in cui il telaio è costituito da più pilastri K=12E/h³(I₁+I₂+...+I_n).

In questa seconda tabella sono riportate le rigidezze di ogni controvento e le rispettive distanze dal punto O.

A questo punto calcoliamo il centro di massa dell'impalcato, il punto in cui verrà applicata la forza sismica; per farlo abbiamo bisogno di ricondurre la pianta dell'impalcato a figure semplici, in questo caso due rettangoli. Dati l'area e il baricentro di ognuno dei due possiamo ricavare le coordinate del centro di massa dell'intera figura  (X_g= A₁*X_g1 + +A₂*X_g2 / A_{tot ;} Y_g= A₁*Y_g1 + A₂*Y_g2 / A_tot).

Possiamo calcolare a questo punto il centro delle rigidezze con il foglio excel. Le cordinate di C sono X_c= K_v1*d_v1 + K_v2*d_v2 + ... + K_vn*d_vn/ K_vtot ; Y_c= K_o1*d_o1 + K_o2*d_o2 + ...... + K_on*d_on/ K_otot .

Il centro di massa ed il centro di rigidezza non coincidono. Poichè la forza del sisma viene applicata nel centro di massa, se questo fosse sullo stesso asse del centro delle rigidezze l'impalcato traslerebbe soltanto; in questo caso subirà anche una rotazione in quanto la distanza fra i due centri diventa il braccio della forza F.

Per calcolare la forza sismica inseriamo nel file excel i dati relativi ai carichi del solaio (G,Q) ed i coefficienti di contemporaneità (ψ) e d'intensità sismica (c) che varia a seconda della zona.

F = W * c , dove W = G + (Q *  ψ) .

L'ultimo step definisce come la forza si ripartisce sui controventi prima in direzione x poi in direzione y e quantifica la cinematica dell'impalcato: traslazione orizzontale, traslazione verticale e rotazione, rispettivamente u = F/k_{o_tot} ,    v = F/k_{v_tot} e  φ = W/kφ .

L'obiettivo dell'esercitazione è quello di dimensionare la sezione di un pilastro nelle tre tecnologie: legno, acciaio e cemento armato.

Si tratta di un pilastro soggetto a sforzo normale di compressione per cui nella progettazione bisogna tener conto anche dell'instabilità. Oltre a definire un'area minima per cautelarsi dalla rottura per schiacciamento (mettendo in relazione σ_max con fyd) definisco anche un momento d'inerzia minimo per evitare che si verifichi il fenomeno dell'instabilità, legato alla snellezza del pilastro (mettendo in relazione σ_max con σ_cr).

Prendo in considerazione un edificio di 4 piani di cui sono sotto riportati una pianta di carpenteria ed una sezione.   Sono evidenziati in rosso il pilasrto maggiormente sollecitato e la sua relativa area di influenza. Tra i pilastri di ogni piano, quello a piano terra sarà più sollecitato rispetto agli altri.

LEGNO:

Nel file excel calcolo per prima cosa l'area di influenza del pilastro (L₁ x L₂) , poi il carico del solaio e quello delle travi, per ottenere lo sforzo totale di compressione N sul pilastro [(q_trave + q_solaio) x n.piani].

Il carico del solaio, dato dai carichi strutturale, permanente e accidentale, è lo stesso delle esercitazioni precedenti; il carico delle travi è dato dal prodotto del peso proprio di ogni trave per la rispettiva lunghezza contenuta nell'area d'influenza.

Inserisco poi nel foglio di calcolo le informazioni relative alla resistenza del materiale (legno strutturale C24) e, dividendo N per f_c0d , ottengo l'area minima per evitare la crisi per schiacciamento.

A questo punto devo calcolare il momento d'inerzia minimo della sezione per evitare che si verifichi il fenomeno dell'instabilità. Qesto è legato alla snellezza (λ) del pilastro, cioè al rapporto tra la sua "altezza" e la sua "larghezza" ossia alla lunghezza libera di inflessione (l₀) diviso il raggio giratore di inerzia (ρ); per questo maggiore è l'inerzia della sezione, minore è λ e minore è il rischio che si verifichi il fenomeno dell'instabilità.

Inseriti i valori del modulo di elasticità (E), di β (legato ai vincoli a cui è soggetto il pilastro analizzato), e dell'altezza del pilastro (l) ricavo quindi il raggio di inerzia minimo che, in casi come questo di sezioni rettangolari, permette di ricavare la base della sezione (piochè ρ_min=√1/12b).

Avendo la base posso ricavare anche un'altezza minima; ingegnerizzo entrambi i valori ed ottengo l'area della mia sezione che dovrò confrontare con l'area minima ricavata all'inizio: la sezione risulterà verificata se, e solo se, A_design > A_min

ACCIAIO:

Anche per il pilastro in acciaio, dopo aver ricavato l'area d'influenza, il carico delle travi e quello del solaio, ottengo lo sforzo di compressione N.

Inserisco i valori di resistenza dell'acciaio (S235) ed ottengo l'area minima per evitare la rottura.

Inserisco poi i valori del modulo di elasticità (E), dell'altezza del pilastro (l) e di β (β  = 1 anche in questo caso perchè ci troviamo in presenza di un nodo di tipo "cerniera", quindi di una trave doppiamente appoggiata).  Ottengo così il momento d'inerzia minimo (Axρ²_min) che mi permette di scegliere un profilato dalla tabella delle HEA.

Nel mio caso una HEA140.

CEMENTO ARMATO:

Anche in questo caso calcolo l'area di influenza del pilastro, il carico delle travi e quello del solaio per ricavare lo sforzo di compressione N.

Inserisco la tensione di resistenza caratteristica f_ck da cui ottengo quella di progetto f_cd e da N/f_cd ricavo un'area minima per la sezione del pilastro.

Inserisco poi i valori del modulo di elasticità (E), di β e dell'altezza del pilastro (l) per trovare una base minima e di conseguenza un'altezza minima.

Il β in questo caso sarà 0,5 poichè siamo in presenza di un nodo di tipo "incastro";per questo motivo il momento a cui la trave è soggetta si trasferisce sul pilastro che dovrò quindi verificare a presso-flessione.

Devo quindi ingegnerizzare base e altezza minime in modo da verificare la condizione: σ_max≤f_cd .

L'esercitazione consiste nel dimensionare una mensola (nei tre sistemi costruttivi di legno, acciaio e c.a.) e di calcolarne l'abbassamento massimo.

Uso lo stesso solaio di carpenteria della prima esercitazione (dimensionamento di una trave) aggiungendogli uno sbalzo di 2m.

SOLAIO IN LEGNO

Dati i carichi calcolati nel precedente solaio li adatto alla porzione di solaio portato dalla mensola più sollecitata (quello evidenziato in rosso). Trovato il carico ultimo (qu) posso ricavare il momento massimo, che in una mensola è q_u*l²/2. Inseriti poi i valori caratteristici del legno (lamellare GL24H) per ricavare la tensione di progetto (fd)  ipotizzo una base per la sezione della mensola da cui ottengo un'altezza da ingegnerizzare.

Ne risulta che la mensola ha una sezione di 25cmX45cm.

Inseriti poi dati relativi all'elasticità del materiale ed all'inerzia della sezione ricalcolo il carico ultimo allo stato limite di esercizio (qe) poichè l'abbassamento che ci interessa calcolare non porta al collasso della struttura ma ad una sua perdita di funzionalità.

A questo punto posso calcolare l'avvassamento v_max=q_e*l⁴/8*E*I_x .

Per capire se è un abbassamento eccessivo faccio riferimento alla disequazione l/v_max >= 250 .

SOLAIO IN ACCIAIO

Allo stesso modo calcolo il carico ultimo ed il momento massimo anche nella mensola in acciaio; inseriti poi i dati relativi alla tensione dell'acciaio (S235) posso calcolare il modulo di resistenza W_x,min in base al quale scelgo la trave dalla tabella delle IPE.

Scelgo una IPE270 della quale inserisco in tabella peso e momento d'inerzia.

Calcolo il q_e e di conseguenza l'abbassamento massimo. Infine verifico che l/v_max >= 250 .

SOLAIO IN CEMENTO ARMATO

Calcolati anche per la mensola in c.a. il carico ultimo ed il momento massimo ed inseriti i dati tensionali sia dell'acciaio delle barre, sia del calcestruzzo, ricavo le tensioni di progetto di entrambi i materiali (fyd, fcd); imposto una base per la trave (scelgo 25cm + 5cm di copriferro) e ricavo un'altezza minima di 25,42cm che ingegnerizzo a 35cm. A questo punto ricavo il peso unitario della trave che andrò a sommare al carico strutturale qs per verificare l'altezza ottenuta.

Inseriti i dati relativi all'inerzia, al peso ed all'elasticità della trave calcolo il q_e e di conseguenza l'abbassamento massimo. Infine verifico che l/v_max >= 250 .

L'esercitazione è incentrata su modellazione, analisi e dimensionamento di una travatura reticolare.

Con il software SAP2000 ho scelto di modellarne una a base quadrangolare, il cui modulo misura 2m: ho ottenuto così una griglia tridimensionale di coordinate z=2, x=5, y=4.

Il modello è costituito da 12 cubi, ognuno dei quali formato da aste verticali ed orizzontali di 2m ed aste oblique di 2,83m.

Dopo aver controllato che non ci fossero duplicati delle aste nel modello, ho assegnato ai quattro spigoli della griglia dei vincoli esterni di tipo cerniera ed ai nodi interni dei vincoli di tipo cerniera interna, assegnando valore zero al momento nei nodi poichè una travatura reticolare lavora solo a sforzo normale.

Ho scelto poi un tubolare in acciaio ed uno schema di carico (F) per la struttura ed infine ho assegnato un carico di 80 kN per ogni nodo superiore.

A questo punto ho fatto partire l'analisi lineare statica relativa al carico F.

Ho ottenuto una deformata,

 ed uno schema dei diagrammi delle sollecitazioni che, come ho gia detto, in una reticolare è relatvo solo allo sforzo normale: di trazione o di compressione.

Ho poi esportato i valori di N relativi alle aste in un file excel, eliminando i duplicati ed evidenziando in rosso le aste diagonali per distinguerle da quelle orizzontali e verticali per procedere quindi al dimensionamento. 

Per quanto riguarda i valori di trazione, ho usato una nuova tabella in cui ho messo in realzione tali valori con le caratteristiche del materiale (fyk,Ym) per ricavare un'area minima (N/fyd) dalla quale partire per il dimensionamento delle aste usando la tabella dei profilati metallici.Per i valori di compressione ho ricavato allo stesso modo un'area minima ma prima di passare al dimensionamento ho dovuto inserire altri valori: questo perchè per la compressione bisogna tener conto dell'instabilità e considerare quindi anche la luce delle aste, la loro geometria, qundi l'inerzia ed anche l'elasticità del materiale. Una volta inseriti i valori relativi a queste caratteristiche, in particolare lambda, rho_min e I_min ho potuto dimensionare le aste tramite la tabella dei profilati.

SOLAIO DI CARPENTERIA

Progetto della trave centrale, che risulta essere la più sollecitata, assumendo prima un solaio in legno, poi uno in acciaio ed infine uno in cemento armato.

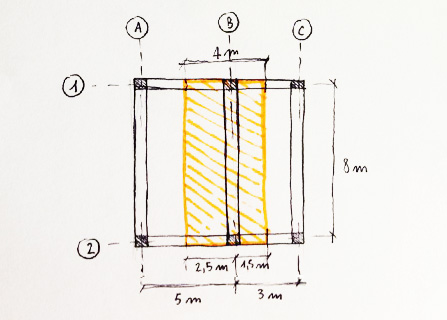
SOLAIO IN LEGNO

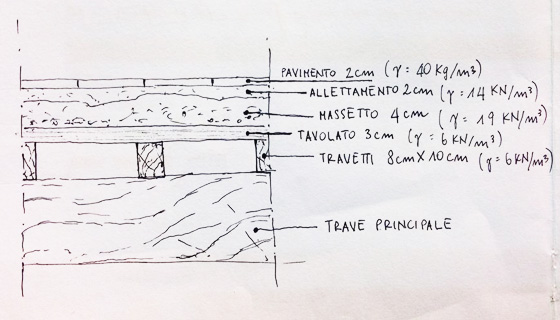
Definito un solaio "tipo" calcolo i carichi agenti su un metro quadro di tale solaio moltiplicando ogni elemento del pacchetto per il proprio peso specifico --> carico = peso specifico[kN/mc] x volume[mc] / [mq]

CARICO STRUTTURALE (qs) :

travetti: 6[kN/mc] x 2 x (0,1 x 0,08)[mc]/[mq] = 0,096[kN/mq]

tavolato: 6[kN/mc] x 0,03[mc]/[mq] = 0,18[kN/mq]

qs = 0,096 + 0,18[kN/mq] = 0,276[kN/mq]

CARICO PERMANENTE (qp) :

massetto: 19[kN/mc] x 0,04[mc]/[mq] = 0,76[kN/mq]

allettamento: 14[kN/mc] x 0,02[mc]/[mq] = 0,28[kN/mq]

pavimento: 0,4[kN/mq]

qp: 0,76 + 0,28 + 0,4 + 1,5(impianti+tramezzi)[kN/mq] = 2,94[kN/mq]

CARICO ACCIDENTALE (qa) = 2[kN/mq]

Inserito il valore dei carichi nella tabella excel posso calcolare il CARICO TOTALE (qu) sommando i vari carichi moltiplicati per un coefficiente di sicurezza.

Dato il carico ultimo, inserendo la luce della trave, posso ricavare dalla tabella il momento massimo (dall'equazione qul^2/8).

A questo punto imposto una fmk=24MPa (di un legno C24) ed un kmod=0,8 (per carichi di media durata) e con un gamma=1,45 posso ricavare dalla tabella la tensione di progetto (fd).

Infine imposto una base (35cm) per ricavare un'altezza minima che ingegnerizzo a 60cm.

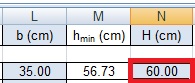
La trave progettata ha dunque una sezione di 35cmx60cm.

SOLAIO IN ACCIAIO

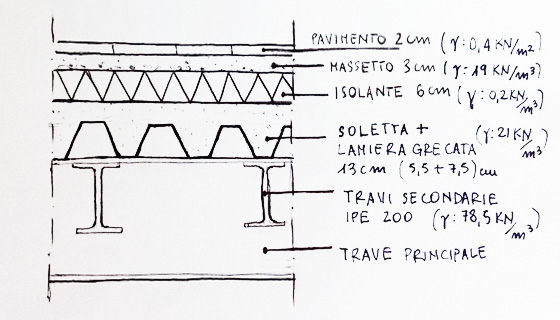
calcolo i carichi agenti su un metro quadro di solaio --> carico = peso specifico[kN/mc] x volume[mc] / [mq]

CARICO STRUTTURALE (qs) :

travi secondarie: 78,5[kN/mc] x 2(0,0028)[mq/[m] = 0,44[kN/mq]

lamiera grecata: 21[kN/mc] x (0,055 + 0,075/2)[mc/mq] = 1,94[kN/mq]

qs =  0,44[kN/mq] + 1,94[kN/mq] = 2,38[kN/mq]

CARICO PERMANENTE (qp) :

isolante: 0,2[kN/mc] x 0,06[mc/mq] = 0,012[kN/mq]

massetto: 19[kN/mc] x 0,03[mc]/[mq] = 0,57[kN/mq]

pavimento: 0,4[kN/mq]

qp: 0,012 + 0,57 + 0,4 + 1,5(impianti+tramezzi)[kN/mq] = 2,48[kN/mq]

CARICO ACCIDENTALE (qa) = 2[kN/mq]

CARICO TOTALE (qu) = (1,3x2,38[kN/mq] + 1,5x2,48[kN/mq] + 1,5x2[kN/mq])x4[m]= 39,26[kN/mq]

Dato il carico ultimo, inserendo la luce della trave, posso ricavare dalla tabella il momento massimo :

A questo punto inserita nella tabella la tensione di snervamento (fyk) dell'acciaio che ho scelto (acciaio S235) posso ricavare la tensione di progetto (fd), dividendo la prima per il coefficiente gamma=1,05.

Ottengo poi il MODULO DI RESISTENZA minimo dividendo l'M max per la tensione di progetto, in base al quale posso scegliere il tipo di trave IPE.

Scelgo una IPE460 il cui Wx è 1500[cmc]

SOLAIO IN C.A.

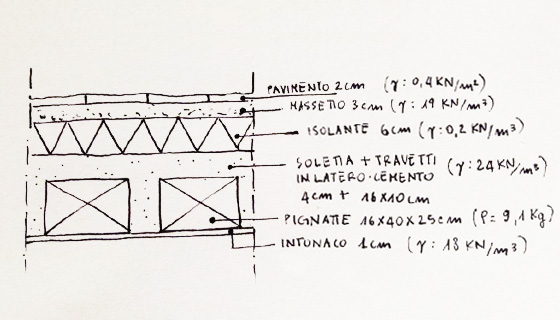
calcolo i carichi agenti su un metro quadro di solaio --> carico = peso specifico[kN/mc] x volume[mc] / [mq]

CARICO STRUTTURALE (qs) :

soletta collaborante: 24[kN/mc] x 0,04[mc/mq] = 0,96[kN/mq]

travetti: 24[kN/mc] x 2(0,16x0,1)[mc/mq] = 0,768[kN/mq]

pignatte: 8 x 0,091[kN/mq]  = 0,728[kN/mq]

qs = 2,45[kN/mq]

CARICO PERMANENTE (qp) :

intonaco: 18[kN/mc] x 0,01[mc]/[mq] = 0,18[kN/mq]

isolante: 0,2[kN/mc] x 0,06[mc/mq] = 0,012[kN/mq]

massetto: 19[kN/mc] x 0,03[mc]/[mq] = 0,57[kN/mq]

pavimento: 0,4[kN/mq]

qp = 2,66[kN/mq]

CARICO ACCIDENTALE (qa) = 2[kN/mq]

CARICO TOTALE (qu) = (1,3x2,45[kN/mq] + 1,5x2,66[kN/mq] + 1,5x2[kN/mq])x4[m] = 40,70[kN/mq]

Dato il carico ultimo, inserendo la luce della trave, posso ricavare dalla tabella il momento massimo :

Inseriti i dati tensionali sia dell'acciaio delle barre, sia del calcestruzzo, dalla tabella ricavo le tensioni di progetto di entrambi i materiali (fyd, fcd).

imposto una base per la trave (scelgo 30cm) e ricavo un'altezza minima di 41,29cm che ingegnerizzo a 45cm. A questo punto ricavo il peso unitario della trave che andrò a sommare al carico strutturale qs per verificare l'altezza ottenuta.

la trave che ho progettato ha una sezione 30cm x 45cm. 

ciaooo!:)