Quinta Esercitazione_Ripartizione forza sismica

La quinta esercitazione consiste nel calcolare come i diversi telai che costituiscono la struttura, si ripartiscano una forza orizzontale (forza sismica o del vento), applicando il metodo delle rigidezze.
Come modello di studio prendo in considerazione un piano tipo del mio progetto del Laboratotio 1MA. La tecnologia dell’impalcato è il cemento armato ed è costituito da telai di tipo Shear-Type (in maniera tale da esser coerente con il foglio excel datoci a disposizione, senza modificare la parte riguardante la rigidezza dei controventi).

Il primo step consiste nel disegno della pianta strutturale dell’edificio preso come modello di studio. Nel mio caso individuo un totale di 22 telai, divisi in:
-14 telai verticali
-8 telai orizzontali

I telai che compongono la struttura sono:
1_O, costituito dai pilastri: 1-9-17-23-27-31-35-39
2_O, costituito dai pilastri: 2-10-18
3_O, costituito dai pilastri: 3-11-19-24-28-32-36-40
4_O, costituito dai pilastri: 4-12
5_O, costituito dai pilastri: 5-13
6_O, costituito dai pilastri: 6-14-20-25-29-33-37-41
7_O, costituito dai pilastri: 7-15-21
8_O, costituito dai pilastri: 8-16-22-26-30-34-38-42
1_V, costituito dai pilastri: 1-2-3-4-5-6-7-8
2_V, costituito dai pilastri: 9-10-11-12-13-14-15-16
3_V, costituito dai pilastri: 17-18-19
4_V, costituito dai pilastri: 20-21-22
5_V, costituito dai pilastri: 23-24
6_V, costituito dai pilastri: 25-26
7_V, costituito dai pilastri: 27-28
8_V, costituito dai pilastri: 29-30
9_V, costituito dai pilastri: 31-32
10_V, costituito dai pilastri: 33-34
11_V, costituito dai pilastri: 35-36
12_V, costituito dai pilastri: 37-38
13_V, costituito dai pilastri: 39-40
14_V, costituito dai pilastri: 41-42

Ricordo che la misura da me scelta per i pilastri è di 30x40 cm.
Indico nella struttura i controventi, rappresentandoli in pianta come delle molle. Queste per l’impalcato rappresentano dei vincoli cedevoli elasticamente.

Ho modificato il foglio Excel di default per poterlo adattare al numero dei miei controventi. Nel primo step ricavo la rigidezza traslante di ogni telaio (K=12EI/h^3). Bisogna stare attenti al diverso orientamento dei pilastri poichè questi offrono un momento d’inerzia diverso in base al loro orientamento (bh^3/12). I valori offerti sono 90.000 cm⁴ ed 160.000 cm⁴.

Nella seconda tabella sono riassunte le rigidezze dei controventi analizzati precedentementi e vengono anche riportare le distanze dall’origine di tutti i vincoli cedevoli elasticamente (controventi).

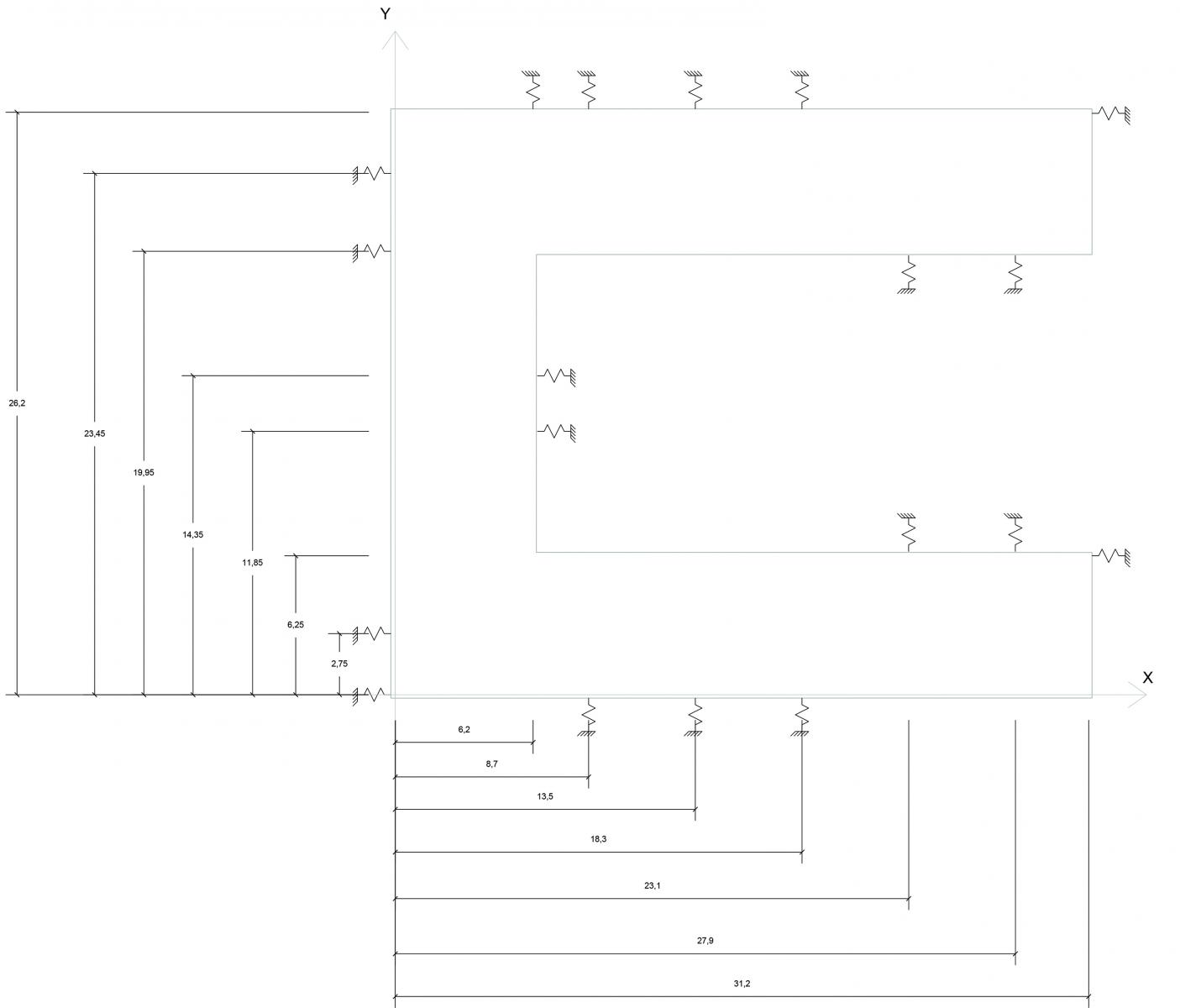
Il passo successivo consiste nel calcolare il centro massa dell’impalcato. Per semplificare le operazioni divido questo in figure geometricamente semplici (rettangoli). Riconosco nel mio impalcato tre rettangoli, di cui due di uguale area. Misuro l’area di questi e la distanza dei loro centri d’area (che in questo caso coincide con il centro delle masse) con l’origine fissata precedentemente. Avendo tutti i dati a disposizione applico una semplice formula per ottenere le due coordinate del centro di massa dell’impalcato:

X_g= A₁*X_g1 + A₂*X_g2 + A₃*X_g3 / A_tot

Y_g= A₁*Y_g1 + A₂*Y_g2 + A₃*Y_g3 / A_tot

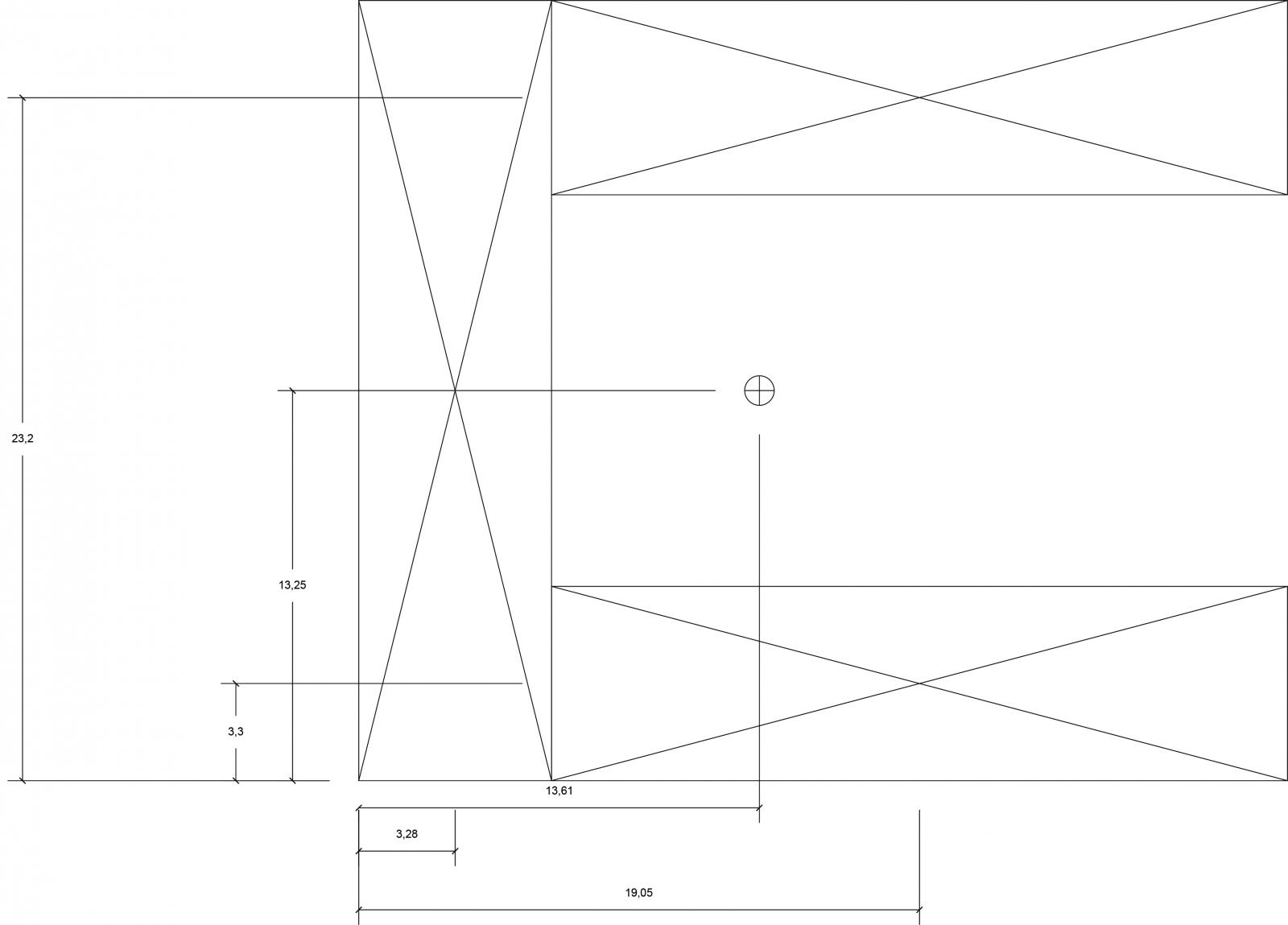
Il quinto step consiste nel ricavare la rigidezza totale dei controventi e le coordinate del centro delle rigidezze. Queste coordinate si trovano applicando le formule:

-X_c= K_v1*d_v1 + K_v2*d_v2 + ...... + K_vn*d_vn/ K_vtot

-Y_c= K_o1*d_o1 + K_o2*d_o2 + ...... + K_on*d_on/ K_otot

Riporto il centro delle rigidezze sulla pianta di carpenteria. Gli scenari possibili sono:
- Caso1= Centro delle masse e centro delle rigidezze coincidono.
In questo caso l’impalcato colpito da una forza lungo X o da una forza lungo Y subirà semplicemente una traslazione.
-Caso2= Centro delle masse e centro delle rigidezze non coincidono.
In questo caso l’impalcato colpito sia da una forza lungo  X o da una forza lungo Y oltre a subire una traslazione semplice, subisce anche una rotazione. In quanto la distanza fra i due centri diventa il braccio della forza F, generando così un Momento.
In conclusione è meglio avere i due centri il più vicino possibile, in modo tale da avere un braccio piccolo e di conseguenza una momento piccolo.

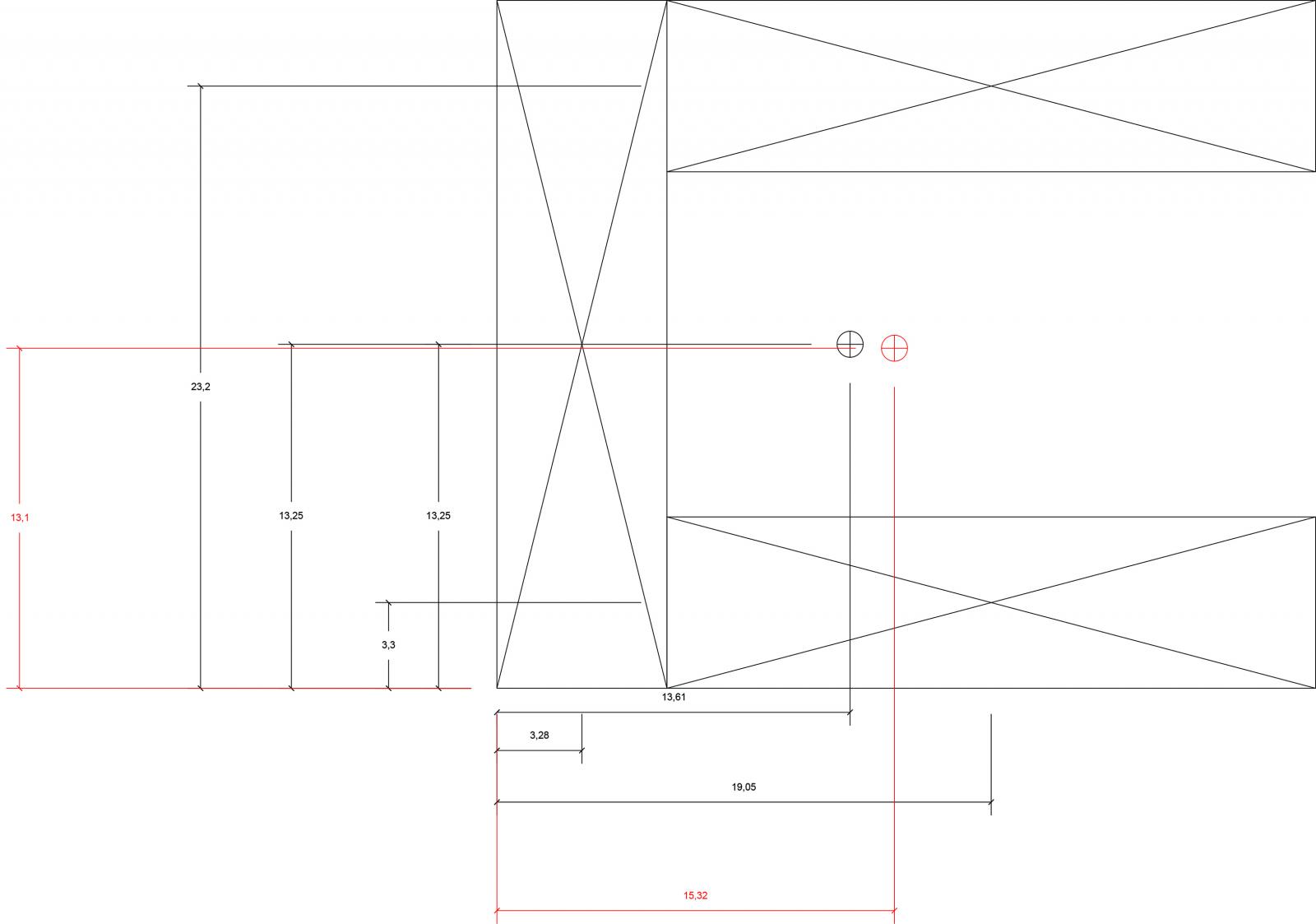
Il mio studio rientra nel secondo caso, ovvero i due centri non coincidono. Di conseguenza le due forze (una lungo X e l’altra lungo Y) genereranno sia una traslazione che una rotazione.
Procedo con il mio studio per ricavare la Forza sismica agente sul centro. Per ottenere questo valore calcolo il carico permanente totale G ed il carico accidentale totale Q, dove:

- G = (q_s + q_p) * A_tot = 2517,94 KN
- Q = q_a * A_tot ​= 2517,94 KN
Step successivo è il alcolo dei pesi sismici (W) attraverso un coefficiente di contemporaneità che è possibile ricavare dalle norme tecniche per le costruzioni. Questo valore è espresso in KN ed è pari ad:

- W = G + (Q *  ψ) = 3273,33 KN

Necessita un ulteriore coefficiente c, che varia in funzione della sismicità della zona. Questo è un valore che va a ridurre l’intensità della Forza sismica, poichè in natura non esiste un terremoto che abbia una accelerazione pari a quella gravitazionale, in quanto questo avrebbe degli effetti catastrofici. Essendo il mio progetto sito a Roma prendo il valore relativo all'area romana, pari ad c= 0,10

Infine la Forza sismica totale è pari ad F = W * c.

I due passaggi conclusivi (step 6 e step 7) analizzano come la forza sismica agisca sui controventi e quali sono gli effetti prodotti su questo (traslazione u_o/v_o e la rotazione φ). Lo step 6 analizza la forza sismica lungo X, mentre lo step 7 analizza lo forza sismica lungo Y.

Gli effetti prodotti saranno:

FORZA SISMICA LUNGO X

 Traslazione

 Rotazione

FORZA SISMICA LUNGO Y

 Traslazione

 Rotazione