In questa prima esercitazione mi sono cimentato nel progetto di una trave, usando un foglio di calcolo elettronico Excel, con tre tecnologie diverse:
- cemento armato
- legno
- acciaio.
Per il progetto del solaio con ognuna di queste tre tecnologie considero un'unica pianta di carpenteria:
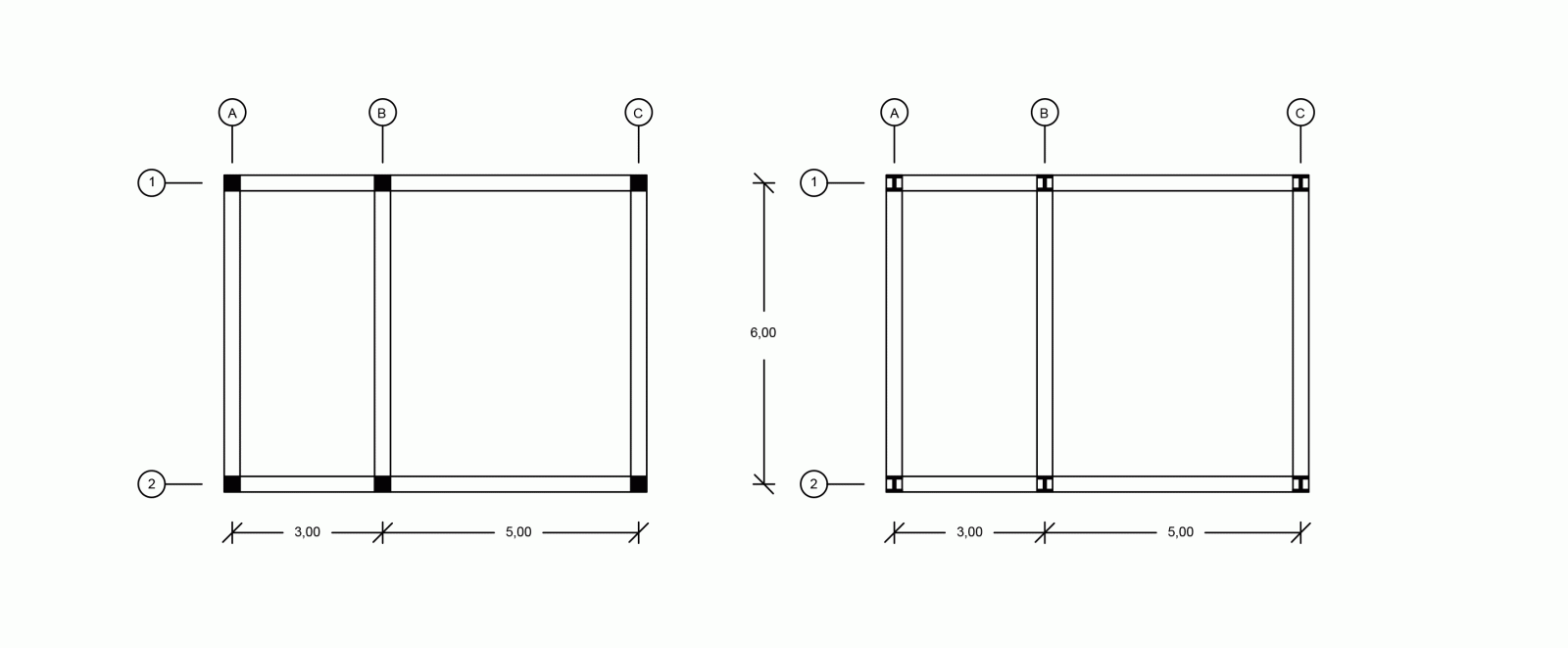
La prima pianta la posso utilizzare per rappresentare il solaio in legno ed in cemento armato, mentre la seconda riguarda il materiale acciaio.
La trave più influenzata è la trave B, per questo motivo procedo con il dimensionamento di quest'ultima, che ha interasse 4m e luce 6m:
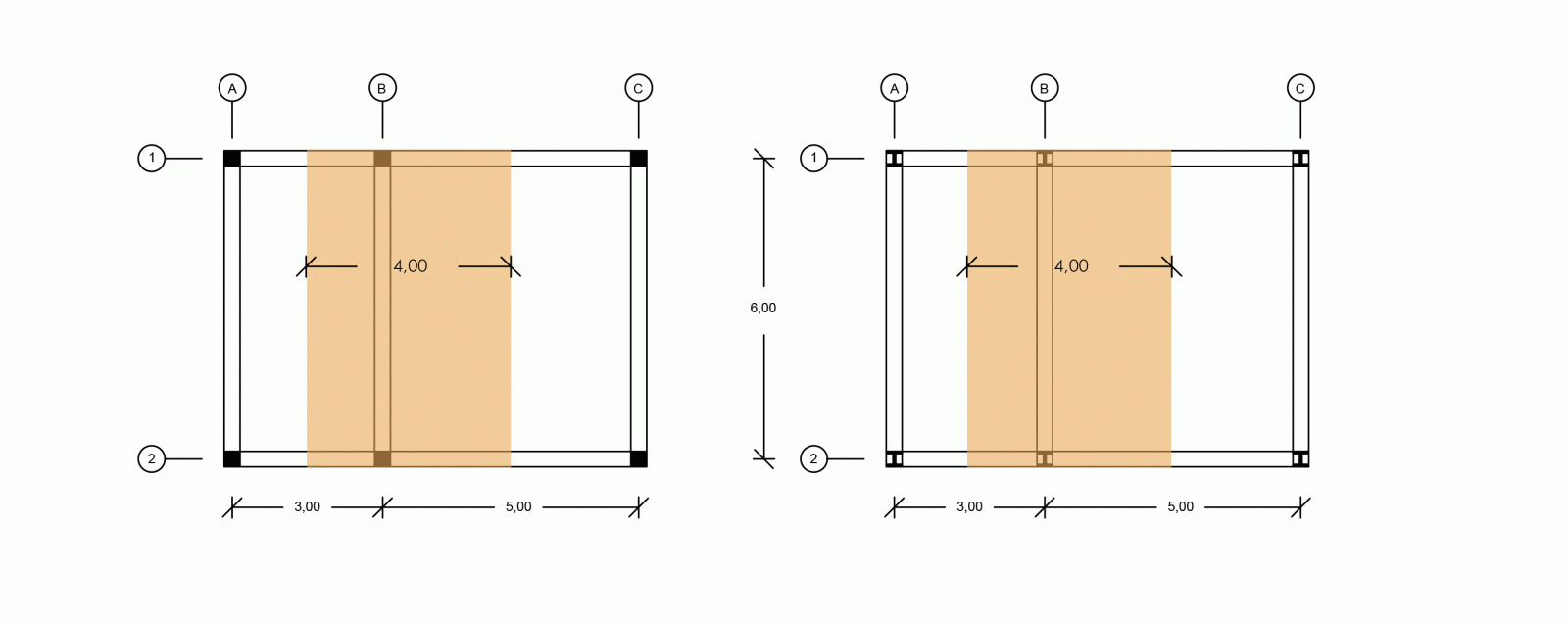
Adesso procedo con l'analisi delle tre sezioni ed il calcolo dei carichi. Il foglio di calcolo elettronico mi agevola nel dimensionamento della trave,
in quanto inserendo dei dati relativi alla geomentria del solaio (luce ed interasse), caratteristiche dei materiali e carichi (qs, qp, qa),
posso procedere con il progetto dell'elemento strutturale.
SOLAIO IN CEMENTO ARMATO
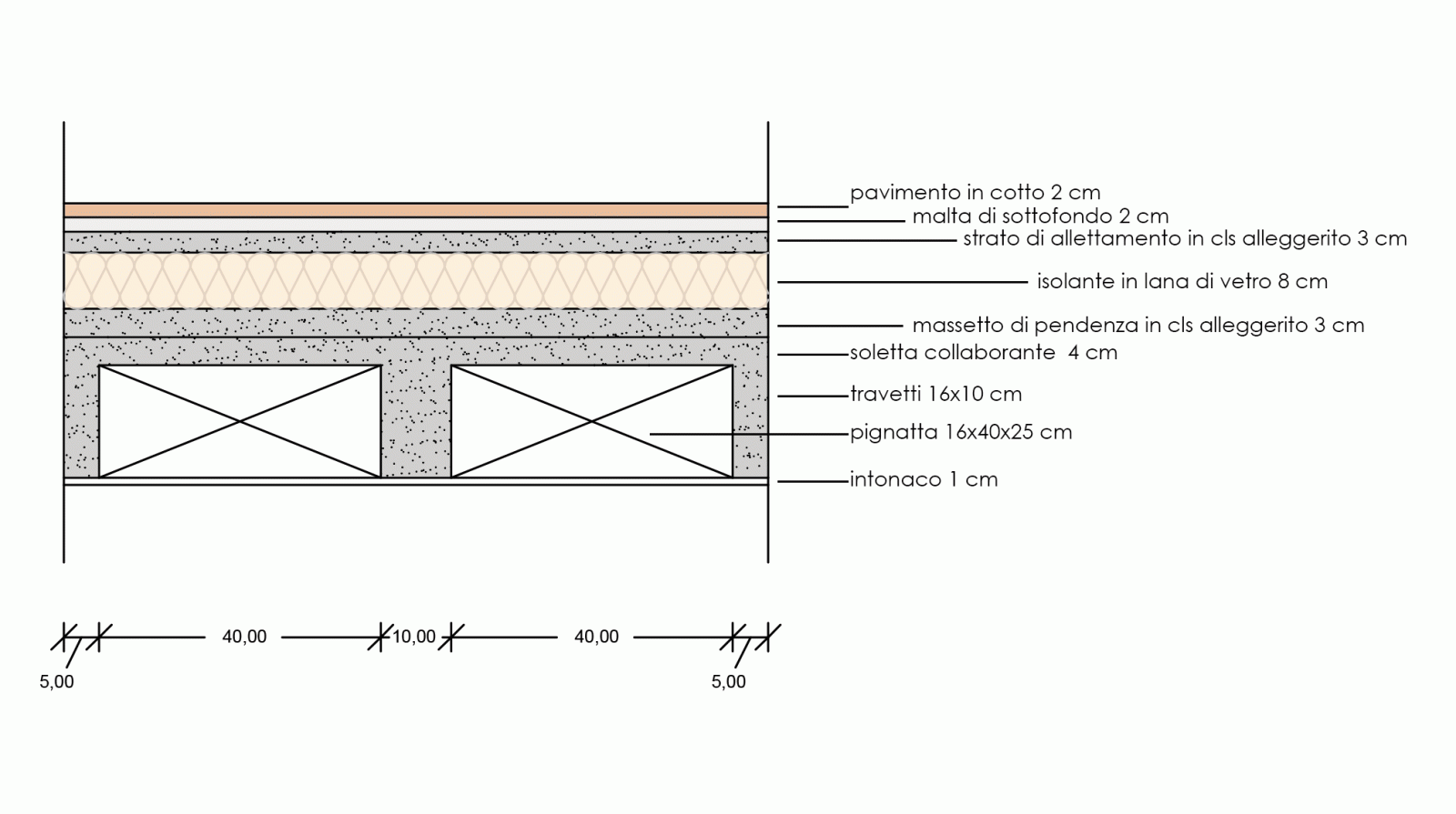
Riporto i dati che mi servono per il calcolo dei carichi qs (carichi strutturali) e qp (carichi portati):
MATERIALE SPESSORE[m]
- pavimento in cotto 24 Kg/mq 0,02
- malta di sottofondo 18 KN/mc 0,02
- strato di allettamento in cls 24 KN/mc 0,03
- isolante in lana di vetro 20 Kg/mc 0,08
- cls alleggerito 18 KN/mc 0,04
- pignatta 9,1 Kg
- intonaco in gesso 13 KN/mc 0,01
qs_carico strutturale (soletta collaborante, travetti, pignatta)
- soletta collaborante: (0,04m x 1m x 1m)/mq x 24KN/mc = 0,96 KN/mq
- travetti: 2(0,10m x 0,16m x 1m)/mq x 24KN/mc = 0,768 KN/mq
- pignatta: 8 x 9,1 Kg/mq = 72,8 Kg/mq = 0,728 KN/mq
qs = (0,96 + 0,768 + 0,728) KN/mq = 2,45 KN/mq
qp_carico portato (pavimento, malta, allettamento, isolante, massetto delle pendenze, intonaco)
- pavimento in cotto: 24Kg/mq = 0,24KN/mq
- malta di sottofondo: (0,02m x 1m x 1m)/mq x 18KN/mc = 0,36KN/mq
- strato di allettamento in cls (0,03m x 1m x 1m)/mq x 24KN/mc= 0,72KN/mq
- isolante in lana di vetro (0,08m x 1m x 1m)/mq x 0,2KN/mc = 0,016KN/mq
- massetto delle pendenze (0,04m x 1m x 1m)/mq x 18KN/mc = 0,72KN/mq
- intonaco (0,01m x 1m x 1m)/mq x 13KN/mc = 0,13KN/mq
- impianti + tramezzi 1,5KN/mq
qp = (0,24 + 0,36 + 0,72 + 0,016 + 0,72 + 0,13 + 1,5)KN/mq = 3,68 KN/mq
qa_carico accidentale
Prendendo la tabella della normativa ho ipotizzato un uso residenziale e quindi:
qa = 2KN/mq
Imposto i seguenti dati sul foglio Excel che di conseguenza mi calcola il qu = (1,3qs + 1,5qp + 1,5qa) x interasse;
inoltre imposto il dato relativo alla luce del solaio, in modo da ottenere il Mmax:

Procedo con l'inserimento dei dati relativi alla resistenza del materiale (fyk, fyd, fck). Infine imposto la dimensione della base della trave
da progettare (io ho scelto 20 cm) e come Hmin ottengo 41,74 cm. Ingegnerizzo questa misura prendendo H = 45 cm. Il peso unitario dell'elemento
da me progettato è pari a 2,25 (KN/m), che si va ad aggiungere al carico qs.
Vengono così calcolati i nuovi dati e la sezione da me scelta (20x45cm) risulta CONFERMATA.
SOLAIO IN LEGNO
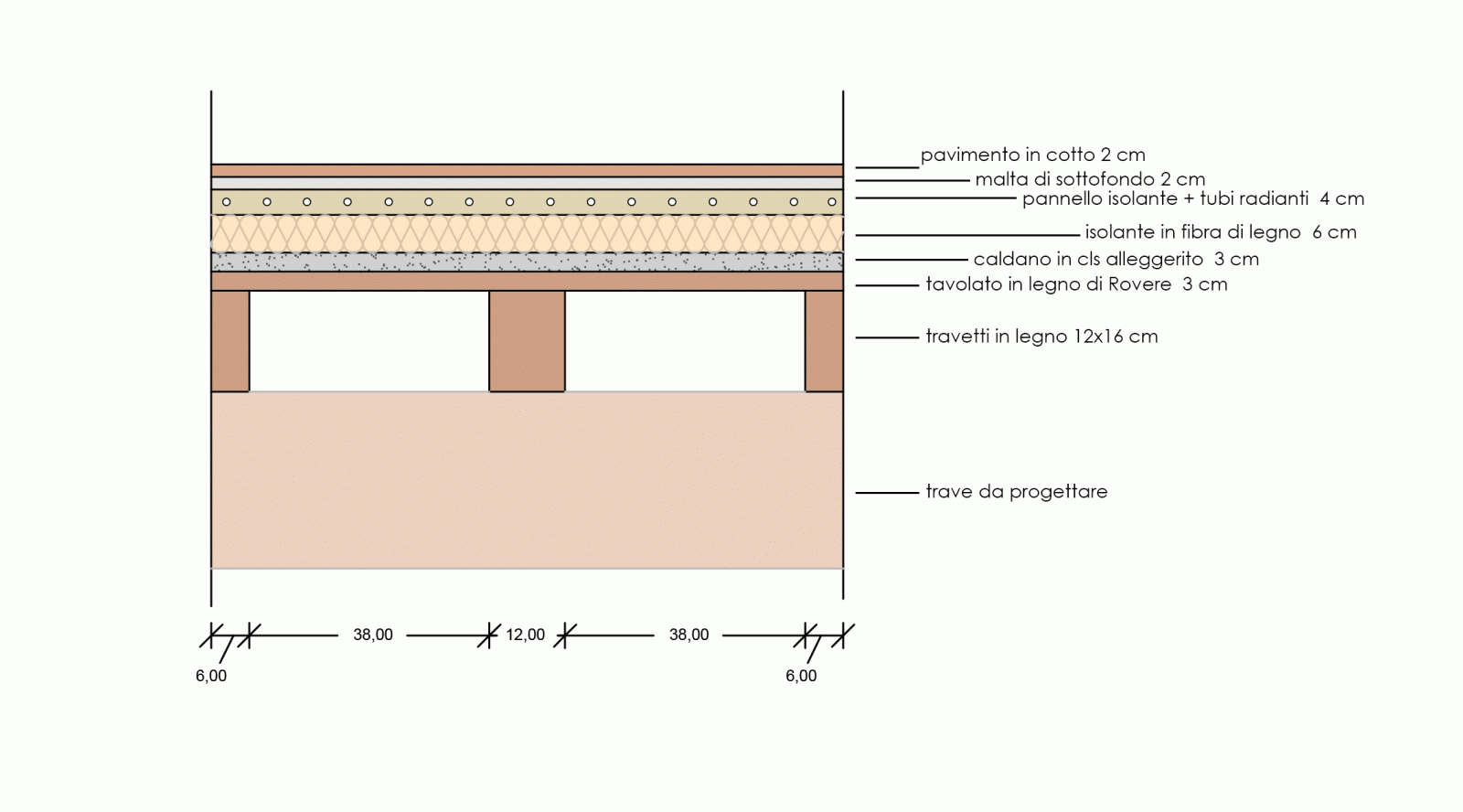
Riporto i dati che mi servono per il calcolo dei carichi qs (carichi strutturali) e qp (carichi portati):
MATERIALE SPESSORE[m]
- pavimento in cotto 24 Kg/mq 0,02
- malta di sottofondo 18 KN/mc 0,02
- pannello isolante + tubi radianti 14,5 KN/mc 0,04
- isolante in fibra di legno 0,18 KN/mc 0,06
- caldana in cls alleggerito 18 KN/mc 0,03
- tavolato in legno di Rovere 7,0 KN/mc 0,03
- travetti in legno 6 KN/mc 0,12 x 0,16
qs_carico strutturale (tavolato, travetti)
- tavolato: (0,03m x 1m x 1m)/mq x 7KN/mc = 0,21KN/mq
- travetti 2(0,12m x 0,16m x 1m)/mq x 6KN/mc = 0,23KN/mq
qs = (0,21 + 0,23)KN/mq = 0,44KN/mq
qp_carico portato (pavimento, malta, pannello radiante, isolante, caldana)
-pavimento in cotto: 24Kg/mq = 0,24 KN/mq
- sottofondo in malta: (0,02m x 1m x 1m)/mq x 18KN/mc = 0,36KN/mq
- isolante + tubi radianti (0,04m x 1m x 1m)/mq x 14,5KN/mc = 0,58KN/mq
- isolante fibra di legno (0,06m x 1m x 1m)/mq x 0,18KN/mc = 0,0108 KN/mq
- caldana in cls alleggerito (0,03m x 1m x 1m)/mq x 18KN/mc = 0,54 KN/mq
- impianti + tramezzi 1,5KN/mq
qp = (0,24 + 0,36 + 0,58 + 0,0108 + 0,54 + 1,5)KN/mq = 3,328KN/mq
qa_carico accidentale
Prendendo la tabella della normativa ho ipotizzato un uso residenziale e quindi:
qa = 2KN/mq
Imposto i seguenti dati sul foglio Excel che di conseguenza mi calcola il qu = (1,3qs + 1,5qp + 1,5qa) x interasse;
inoltre imposto il dato relativo alla luce del solaio, in modo da ottenere il Mmax. Inserisco i dati relativi al tipo di legno
scelto per la trave da progettare ed imposto una base di 30 cm ottenendo una Hmin pari a 48,25 cm.
Ingengerizzo questa misura prendendo H = 55.

SOLAIO IN ACCIAIO
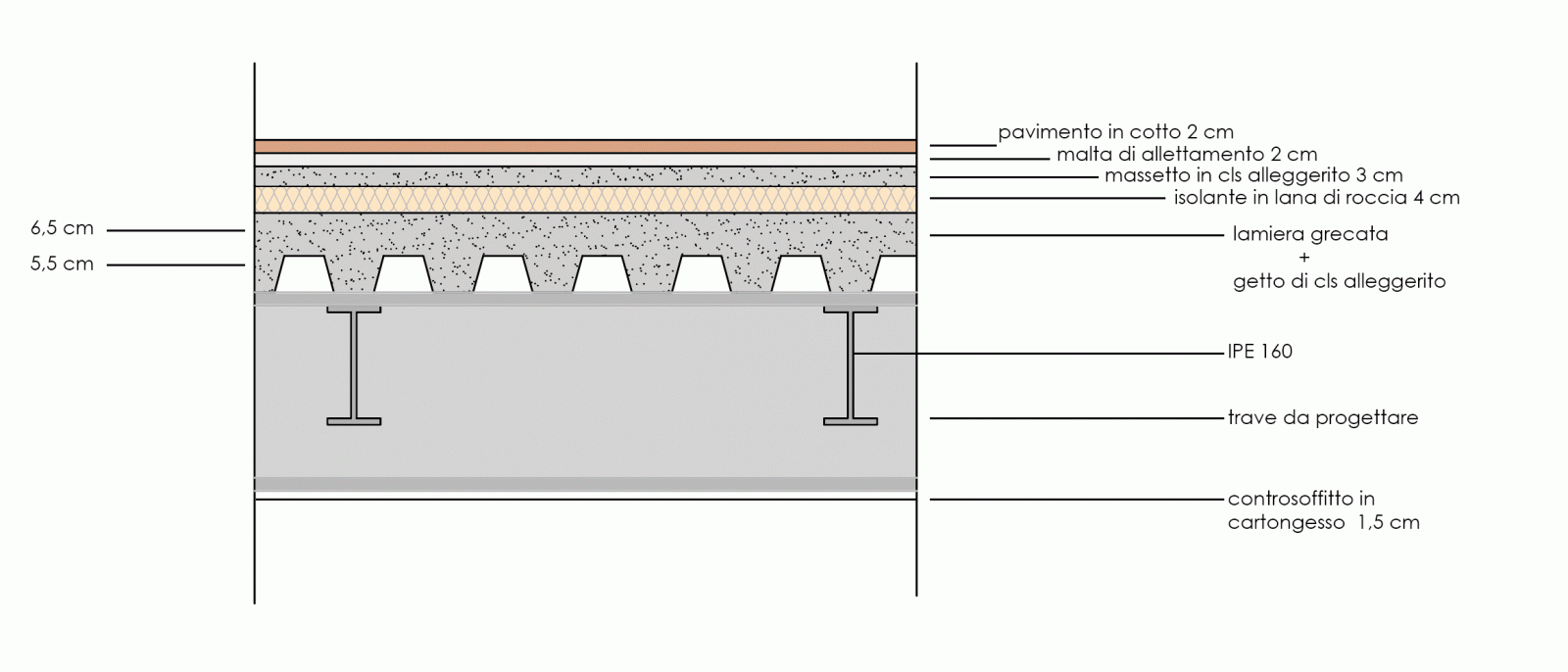
Riporto i dati che mi servono per il calcolo dei carichi qs (carichi strutturali) e qp (carichi portati):
MATERIALE SPESSORE[m]
- pavimento in cotto 24 Kg/mq 0,02
- malta di sottofondo 18 KN/mc 0,02
- massetto in cls alleggerito 18 KN/mc 0,03
- isolante in lana di roccia 90 Kg/mc 0,04
- lamiera grecata 9 Kg/mq
- soletta + metà trapezi 18 KN/mc 0,0925
rimepiti in cls alleggerito
- cartongesso 20 Kg/mq 0,015
- IPE 160 77,1 KN/mc 0,00201 m2
(Area della sezione)
Per semplificarmi i calcoli, quando andrò a calcolare il peso del riempimento in cls della lamiera grecata,
immagino di dividere in due la parte dei trapezi. Così facendo avrò la parte piena che perdo pari a quella vuota,
così posso sommare direttamente lo strato della soletta (6,5 cm) con metà trapezio (5,5cm/2), evitando il
calcolo del singolo trapezio.
qs_carico strutturale (lamiera grecata, getto in cls, IPE 160)
- lamiera grecata: 9Kg/mq = 0,09 KN/mq
- getto in cls alleggerito (0,0925m x 1m x 1m)/mq x 18KN/mc = 1,665KN/mq
- IPE 160 2(0,00201mq x 1m)/mq x 77,1KN/mc = 0,31KN/mq
qs = (0,09 + 1,665 + 0,31)KN/mq = 2,065 KN/mq
qp_carico portato (pavimento, malta di allettamento, massetto in cls alleggerito, isolante, cartongesso)
-pavimento in cotto: 24Kg/mq = 0,24 KN/mq
- sottofondo in malta: (0,02m x 1m x 1m)/mq x 18KN/mc = 0,36KN/mq
- massetto in cls alleggerito (0,03m x 1m x 1m)/mq x 18KN/mc = 0,54KN/mq
- isolante lana di roccia (0,04m x 1m x 1m)/mq x 0,9KN/mc = 0,036KN/mq
- cartongesso 20Kg/mq = 0,2KN/mq
- impianti + tramezzi 1,5KN/mq
qp = (0,24 + 0,36 + 0,54 + 0,036 + 0,2 + 1,5)KN/mq = 2,876KN/mq
qa_carico accidentale
Prendendo la tabella della normativa ho ipotizzato la costruzione di uffici aperti al pubblico:
qa = 3KN/mq
Imposto i seguenti dati sul foglio Excel che di conseguenza mi calcola il qu = (1,3qs + 1,5qp + 1,5qa) x interasse;
inoltre imposto il dato relativo alla luce del solaio, in modo da ottenere il Mmax. Scelgo la fyk dell'acciaio ed ottengo
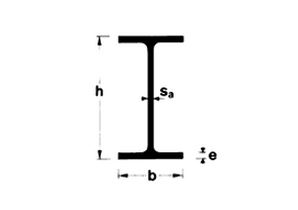
una WX,MIN = 790,26. Prendo la normativa e scelgo il profilato che ha la WX subito più grande rispetto la minima.

Scelgo WX = 904,00cm3, che appartiene alla IPE 360.

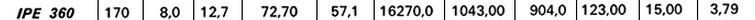
Commenti recenti