ESERCITAZIONE 5_Ripartizione forza sismica

Per questa esercitazione ho calcolato la ripartizione di una forza orizzontale, sismica o del vento, su un telaio di cemento armato utilizzando il metodo delle rigidezze. Come modello di studio ho preso in esame un piano tipo del progetto de Laboratorio di progettazione. I telai sono di tipo Shear-type poichè rappresentano bene i comportamenti dei telai in cemento armato.

- Come prima cosa rappresento la pianta strutturale del mio impalcato individuando 18 telai di cui 12 orizzontali e 6 verticali.

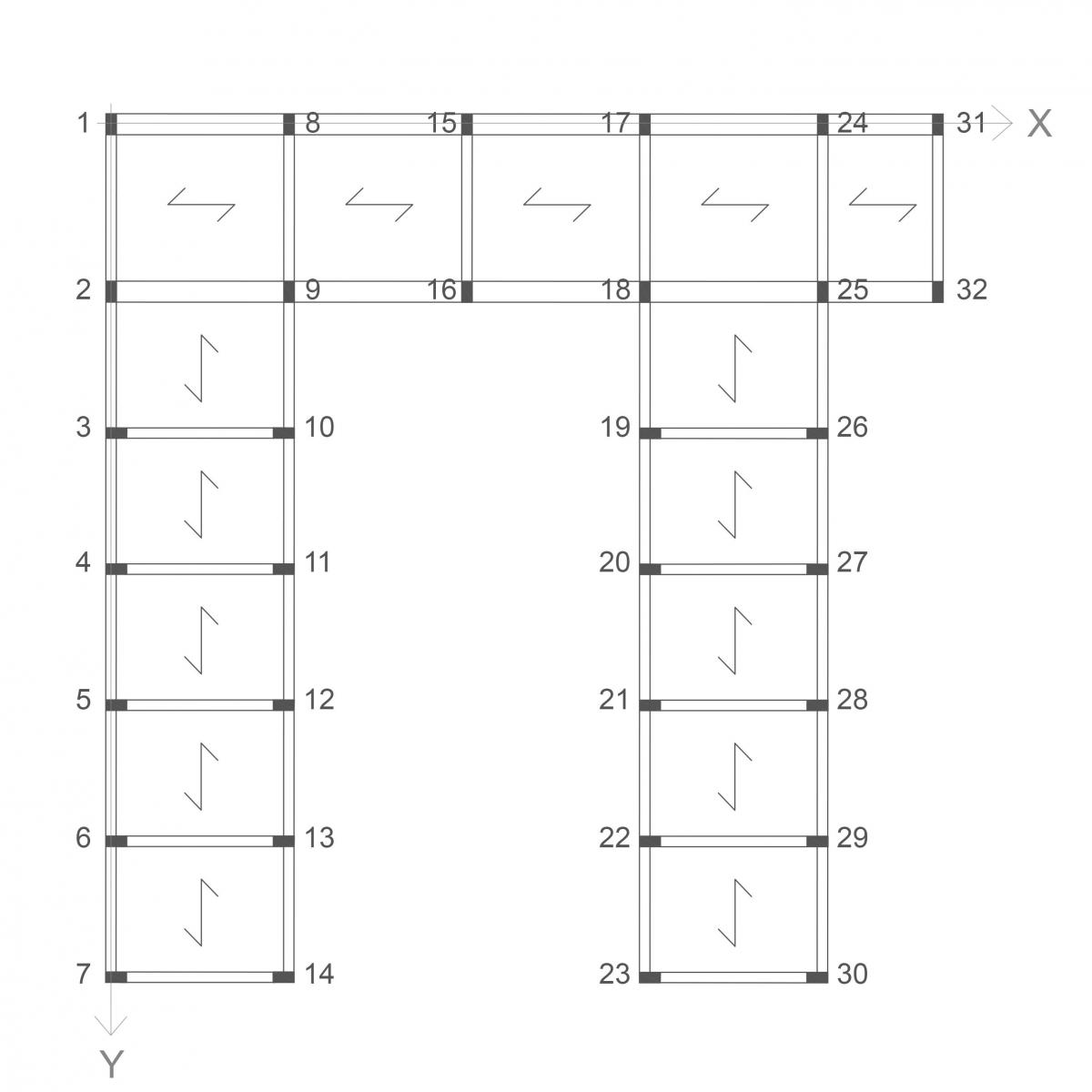- I telai che compongono la struttura sono:

Telaio 1o: 1-8-15-17-24-31

Telaio 2o: 2-9-16-18-25-32

Telaio 3o: 3-10

Telaio 4o: 4-11

Telaio 5o: 5-12

Telaio 6o: 6-13

Telaio 7o: 7-14

Telaio 8o: 19-26

Telaio 9o: 20-27

Telaio 10o: 21-28

Telaio 11o: 22-29

Telaio 12o: 23-30

Telaio 1v: 1-2-3-4-5-6-7

Telaio 2v: 8-9-10-11-12-13-14

Telaio 3v: 15-16

Telaio 4v: 17-18-19-20-21-22-23

Telaio 5v: 24-25-26-27-28-29-30

Telaio 6v: 31-32

-I pilastri utilizzati misurano 60 x 30 cm.

- Come seconda fase rappresento la pianta dei controventi 

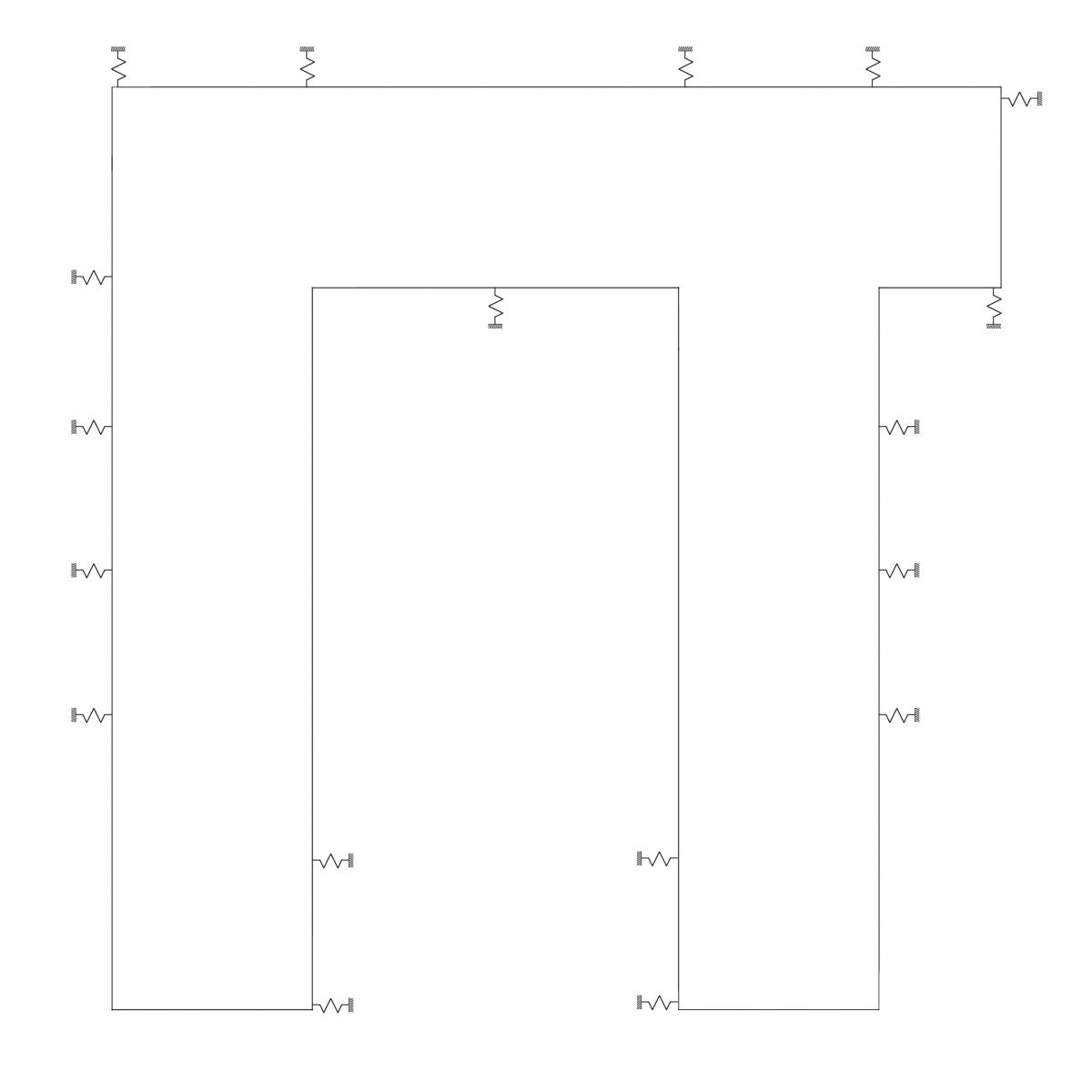- Adesso usufruendo del foglio excel posso ricavare la rigidezza traslante  

K=12EI/h³

 Ovviamente il foglio va modificato per potersi adattare al numero dei contriventi della struttura. Bisogna fare attenzione all'orientamento dei pilastri poichè il momento di inerzia varierebbe in base all'orientamento secondo la formula 

bh³/12

- Nella seconda tabella sono evidenziate le rigidezze dei controventi, verticali ed orizzontali, e le rispettive distanze dal punto di origine O

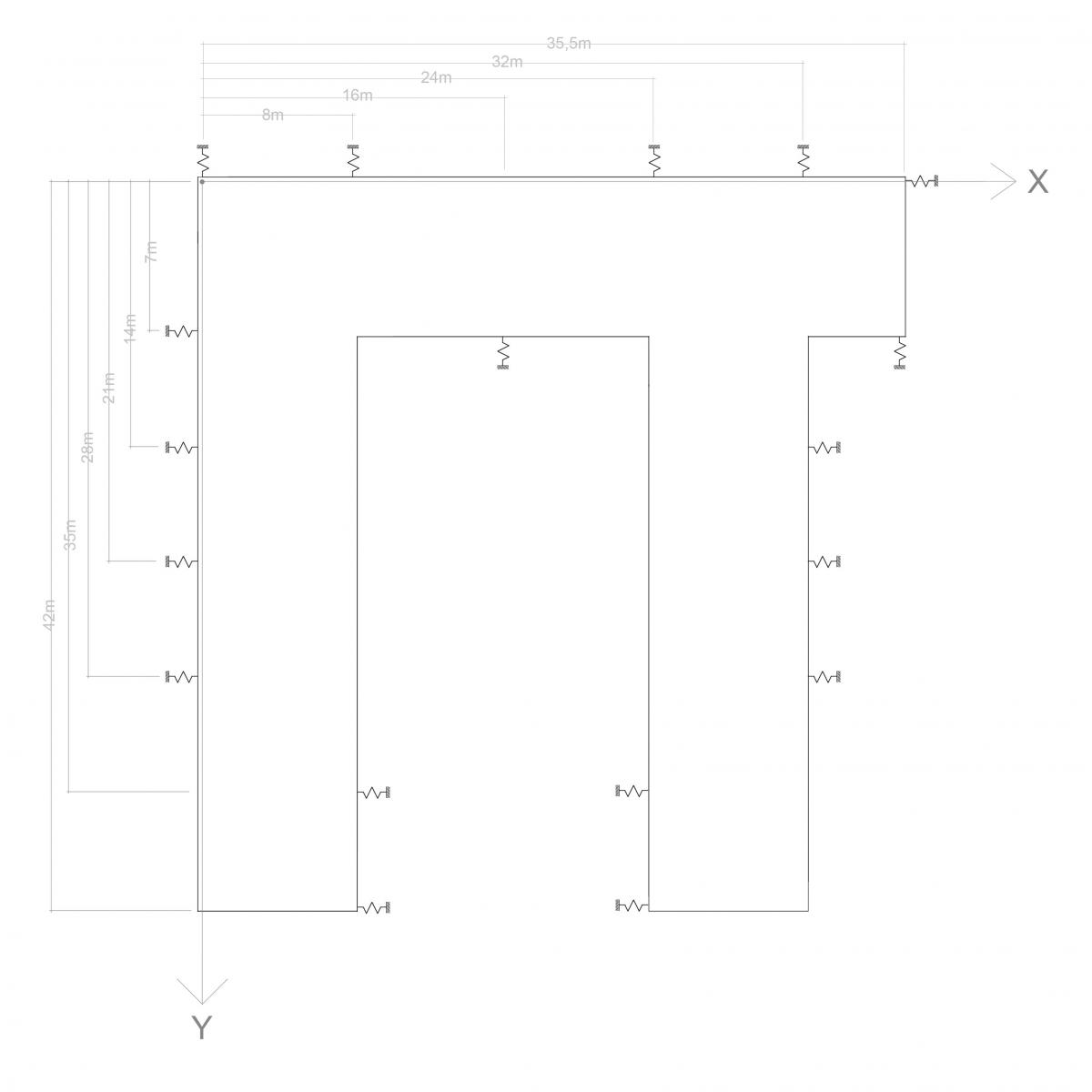
-Per calcolare il centro di massa dell'impalcato divido queto in figure geometriche semplici, inquesto caso rettangoli e ne misuro l'area di ognuno. Calcolo anche la distanza dei loro centri d'area con l'origine e procedo nel calcolare le due coordinate del centro di massa:

X_g= A₁*X_g1 + A₂*X_g2 + A₃*X_g3 / A_tot

Y_g= A₁*Y_g1 + A₂*Y_g2 + A₃*Y_g3 / A_tot

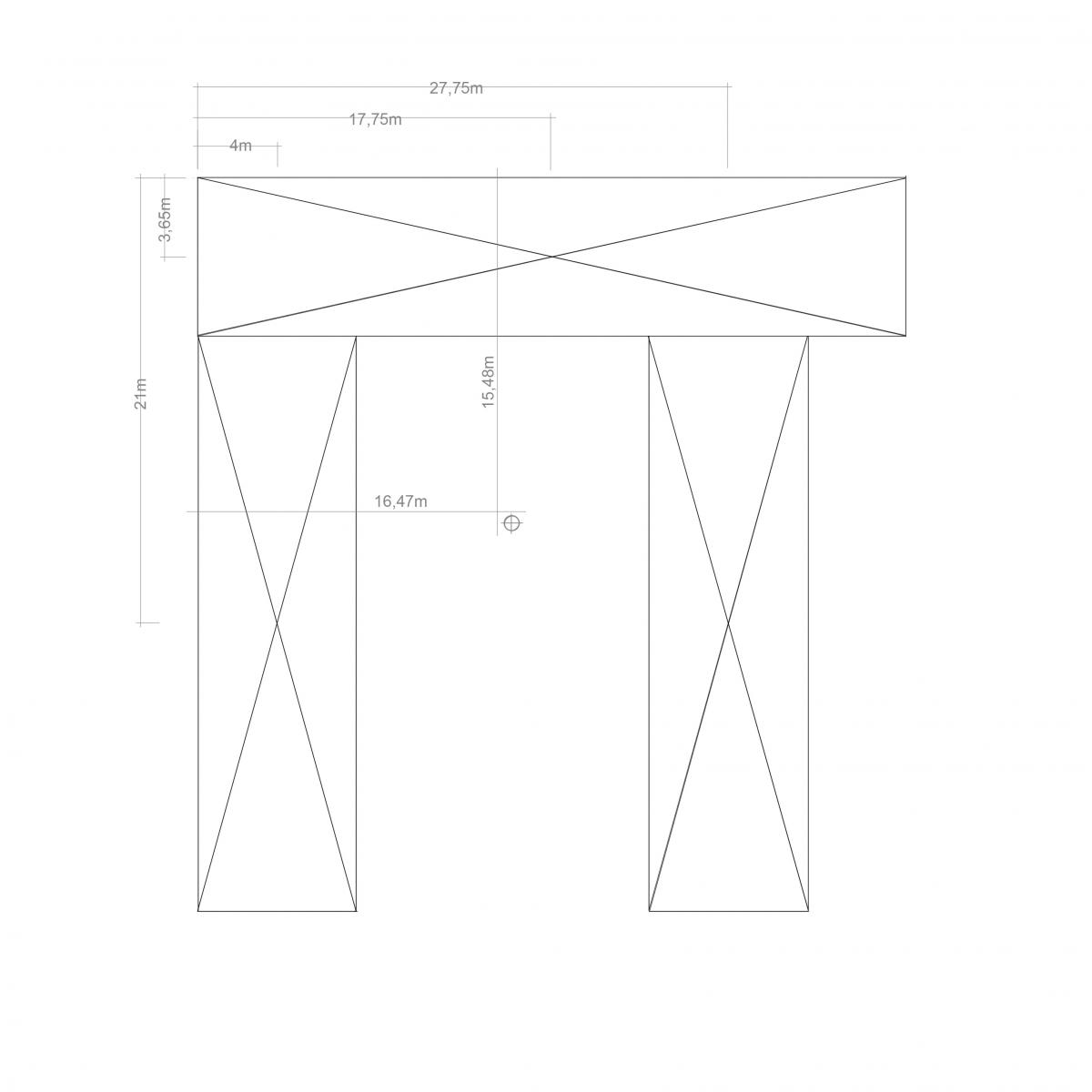
- Successivamente bisogna ricavare la rigidezza totale dei controventi e le cordinate del centro delle rigidezze utilizzando le seguenti formule:

X_c= K_v1*d_v1 + K_v2*d_v2 + ...... + K_vn*d_vn/ K_vtot

Y_c= K_o1*d_o1 + K_o2*d_o2 + ...... + K_on*d_on/ K_otot

Riportando il centro delle rigidezze sulla pianta di carpenteria mi rendo conto che le possibilità sono due e nel caso del mio impalcato sussiste il secondo caso
- Caso1= Centro delle masse e centro delle rigidezze coincidono.
In questo caso l’impalcato colpito da una forza lungo X o da una forza lungo Y subisce una traslazione.

-Caso2= Centro delle masse e centro delle rigidezze non coincidono.
In questo caso l’impalcato colpito sia da una forza lungo  X o da una forza lungo Y oltre a subire una traslazione semplice, subisce anche una rotazione. 

-Procedo con la mia analisi per ricavare la Forza sismica agente sul centro. Per ottenere questo valore calcolo il carico permanente totale G ed il carico accidentale totale Q, dove:

G = (q_s + q_p) * A_tot
Q = q_a * A_tot 

Lo step successivo è il calcolo dei pesi sismici (W) attraverso un coefficiente di contemporaneità che è possibile ricavare dalle norme tecniche per le costruzioni. Questo valore è pari a

W = G + (Q *  ψ) 

Un ulteriore coefficiente c varia in funzione della sismicità della zona; è un valore che va a ridurre l’intensità della Forza sismica. Essendo il mio progetto sito a Roma prendo il valore relativo all'area romana, pari ad c= 0,10

La Forza sismica totale è pari a

F = W * c

- Il sesto e il settimo step analizzano come la forza sismica agisce sui controventi e gli effetti che essa provoca , traslazione e rotazione orizzontali e verticali.

Mentre la sesta tabella permette di calcolare la forza sismica lungo x, la settima tabella quella lungo y.

- Gli effetti prodotti dalla forza sismica sulla struttura saranno:

lungo l'asse x 

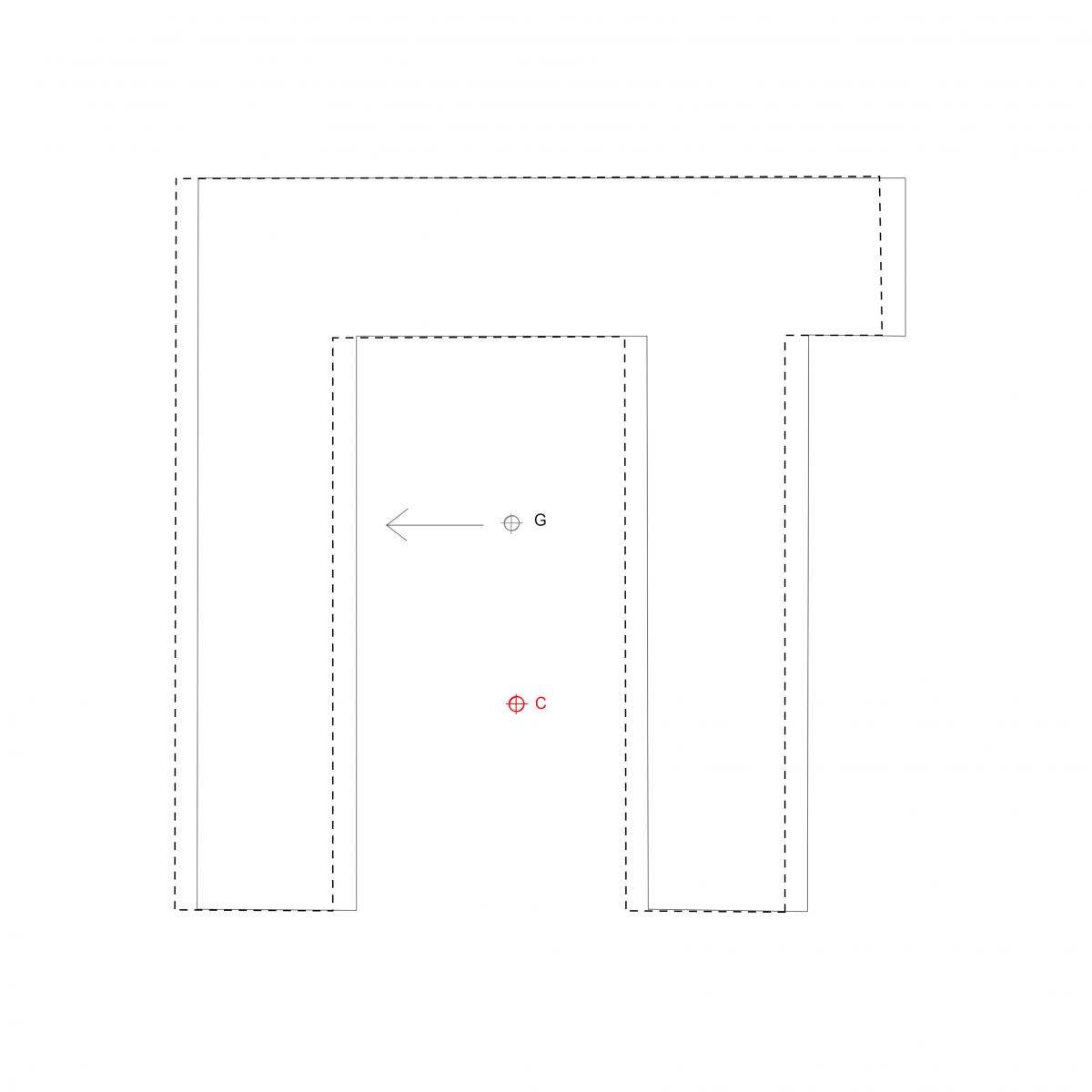traslazione

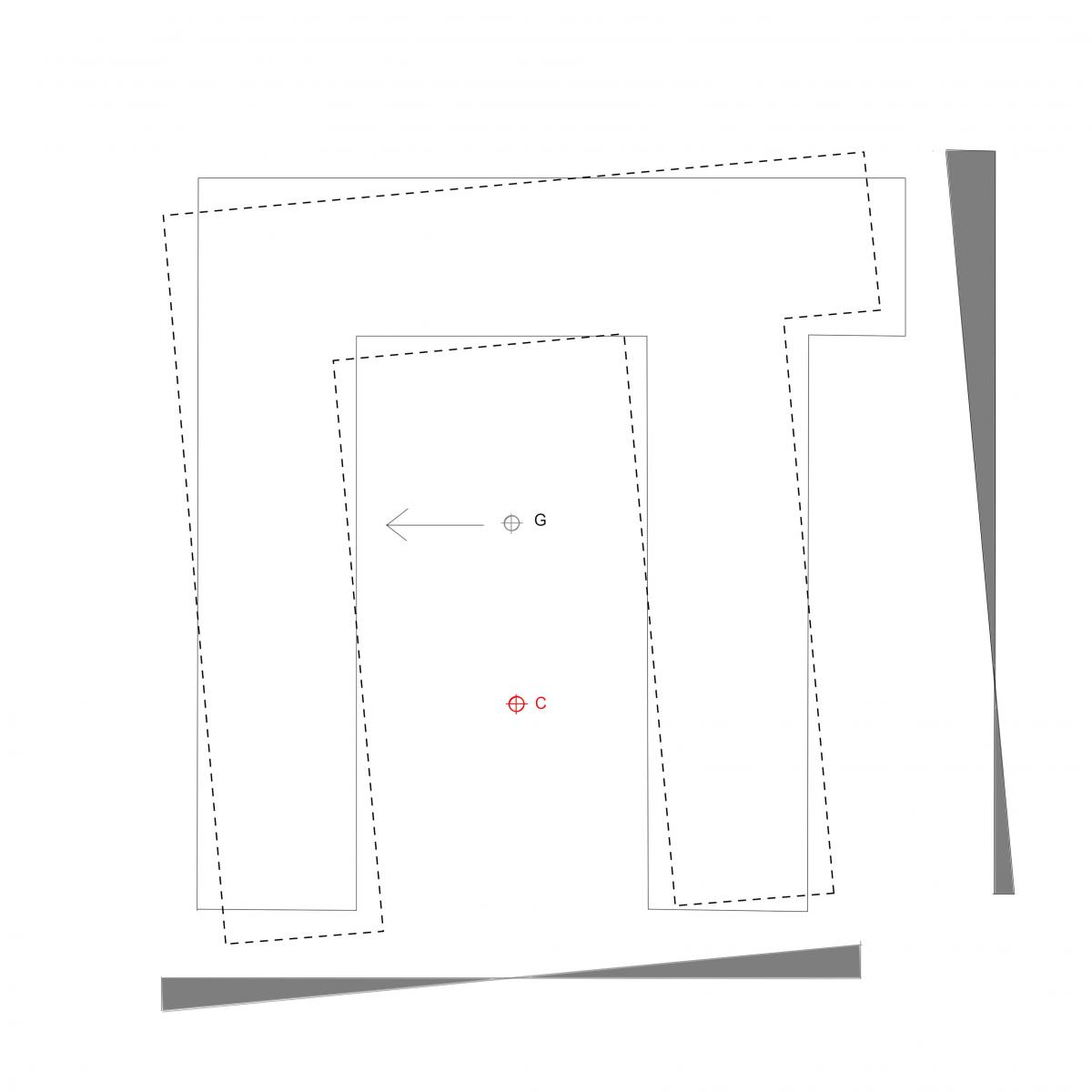rotazione

lungo l'asse y

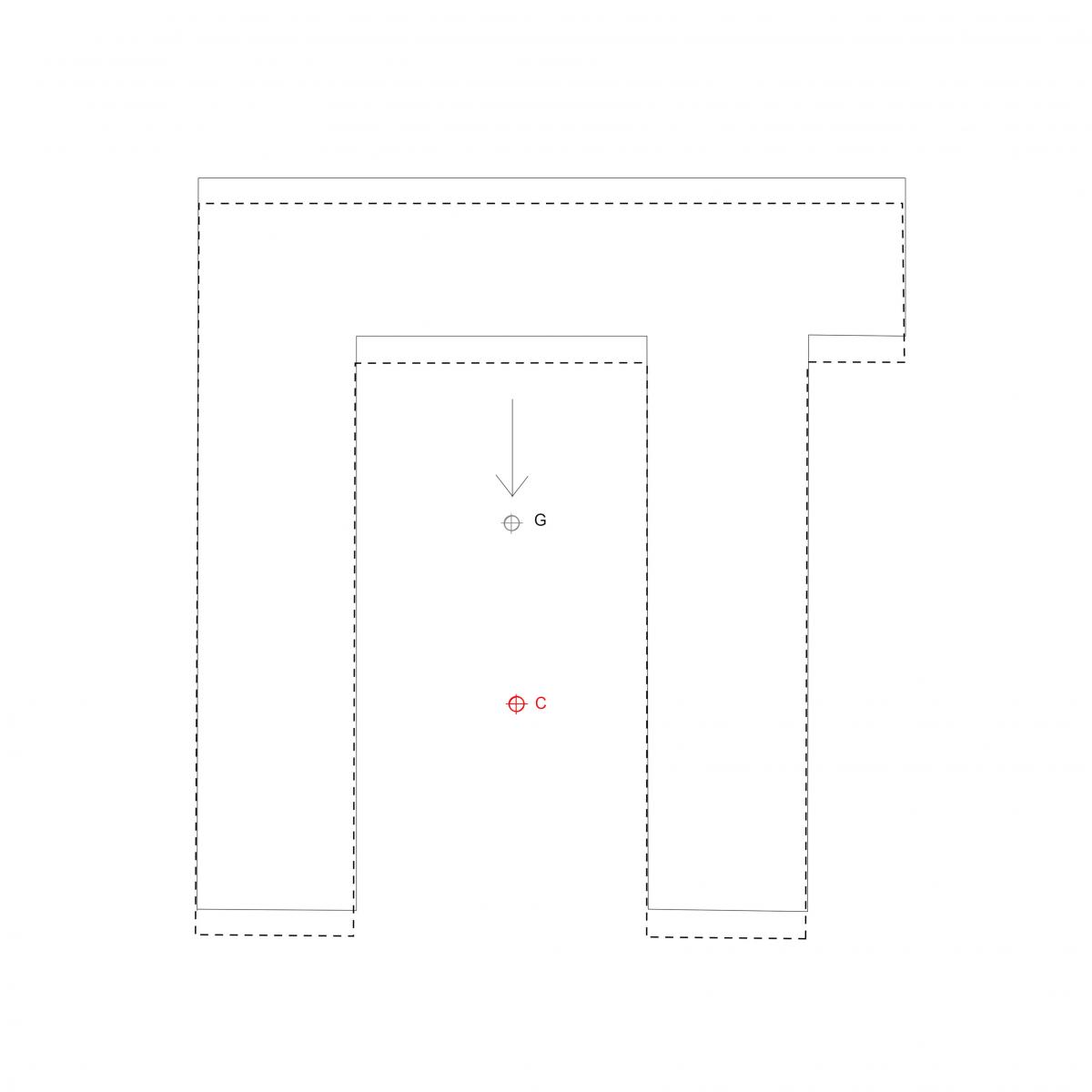traslazione

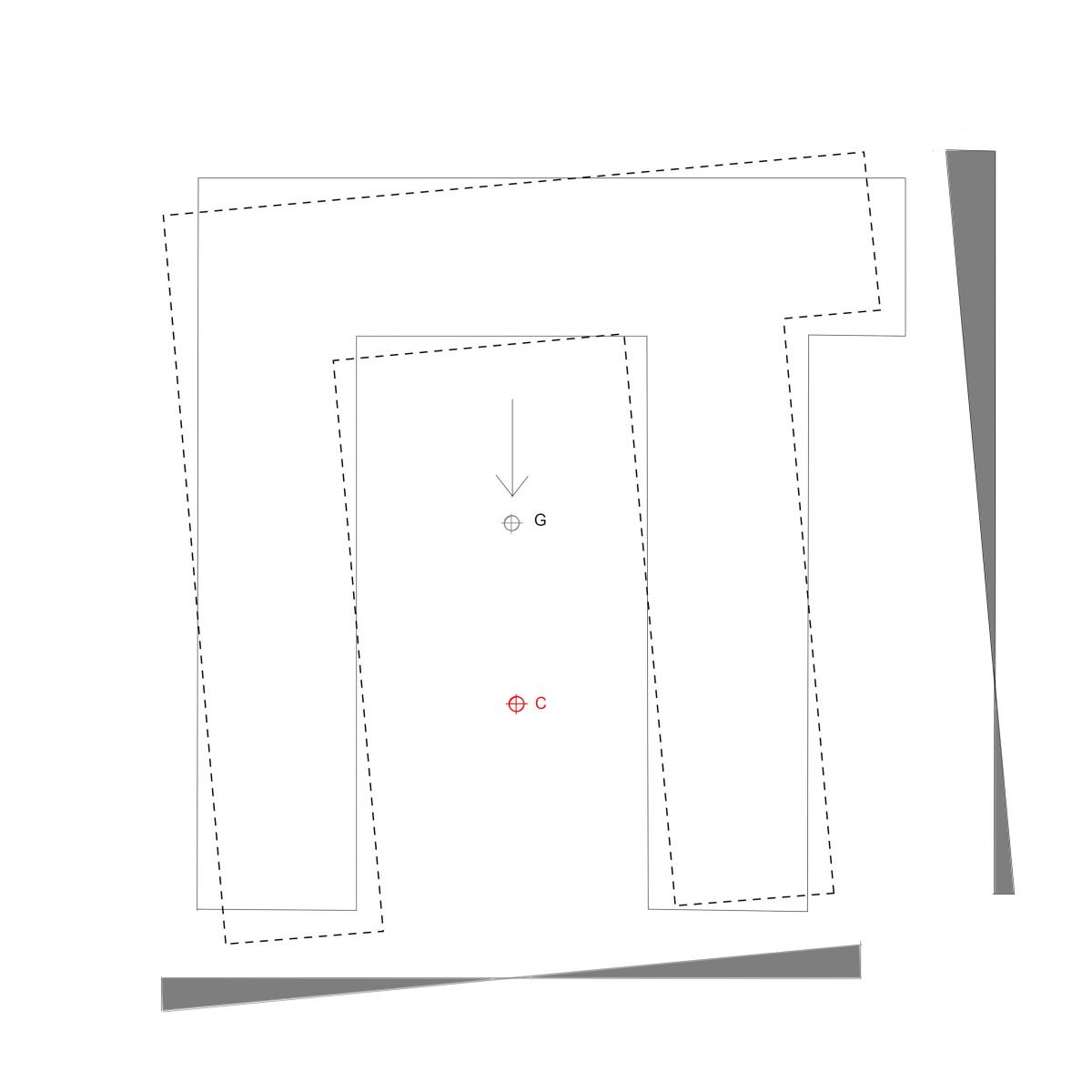rotazione