blog di Francesco Persichella

 

Per questa esercitazione ho calcolato la ripartizione di una forza orizzontale, sismica o del vento, su un telaio di cemento armato utilizzando il metodo delle rigidezze. Come modello di studio ho preso in esame un piano tipo del progetto de Laboratorio di progettazione. I telai sono di tipo Shear-type poichè rappresentano bene i comportamenti dei telai in cemento armato.

- Come prima cosa rappresento la pianta strutturale del mio impalcato individuando 18 telai di cui 12 orizzontali e 6 verticali.

- I telai che compongono la struttura sono:

Telaio 1o: 1-8-15-17-24-31

Telaio 2o: 2-9-16-18-25-32

Telaio 3o: 3-10

Telaio 4o: 4-11

Telaio 5o: 5-12

Telaio 6o: 6-13

Telaio 7o: 7-14

Telaio 8o: 19-26

Telaio 9o: 20-27

Telaio 10o: 21-28

Telaio 11o: 22-29

Telaio 12o: 23-30

Telaio 1v: 1-2-3-4-5-6-7

Telaio 2v: 8-9-10-11-12-13-14

Telaio 3v: 15-16

Telaio 4v: 17-18-19-20-21-22-23

Telaio 5v: 24-25-26-27-28-29-30

Telaio 6v: 31-32

 

-I pilastri utilizzati misurano 60 x 30 cm.

- Come seconda fase rappresento la pianta dei controventi 

- Adesso usufruendo del foglio excel posso ricavare la rigidezza traslante  

K=12EI/h³

 Ovviamente il foglio va modificato per potersi adattare al numero dei contriventi della struttura. Bisogna fare attenzione all'orientamento dei pilastri poichè il momento di inerzia varierebbe in base all'orientamento secondo la formula 

bh³/12

- Nella seconda tabella sono evidenziate le rigidezze dei controventi, verticali ed orizzontali, e le rispettive distanze dal punto di origine O

-Per calcolare il centro di massa dell'impalcato divido queto in figure geometriche semplici, inquesto caso rettangoli e ne misuro l'area di ognuno. Calcolo anche la distanza dei loro centri d'area con l'origine e procedo nel calcolare le due coordinate del centro di massa:

X_g= A₁*X_g1 + A₂*X_g2 + A₃*X_g3 / A_tot

Y_g= A₁*Y_g1 + A₂*Y_g2 + A₃*Y_g3 / A_tot

- Successivamente bisogna ricavare la rigidezza totale dei controventi e le cordinate del centro delle rigidezze utilizzando le seguenti formule:

X_c= K_v1*d_v1 + K_v2*d_v2 + ...... + K_vn*d_vn/ K_vtot

Y_c= K_o1*d_o1 + K_o2*d_o2 + ...... + K_on*d_on/ K_otot

Riportando il centro delle rigidezze sulla pianta di carpenteria mi rendo conto che le possibilità sono due e nel caso del mio impalcato sussiste il secondo caso
- Caso1= Centro delle masse e centro delle rigidezze coincidono.
In questo caso l’impalcato colpito da una forza lungo X o da una forza lungo Y subisce una traslazione.

-Caso2= Centro delle masse e centro delle rigidezze non coincidono.
In questo caso l’impalcato colpito sia da una forza lungo  X o da una forza lungo Y oltre a subire una traslazione semplice, subisce anche una rotazione. 

-Procedo con la mia analisi per ricavare la Forza sismica agente sul centro. Per ottenere questo valore calcolo il carico permanente totale G ed il carico accidentale totale Q, dove:

G = (q_s + q_p) * A_tot
Q = q_a * A_tot 

Lo step successivo è il calcolo dei pesi sismici (W) attraverso un coefficiente di contemporaneità che è possibile ricavare dalle norme tecniche per le costruzioni. Questo valore è pari a

W = G + (Q *  ψ) 

Un ulteriore coefficiente c varia in funzione della sismicità della zona; è un valore che va a ridurre l’intensità della Forza sismica. Essendo il mio progetto sito a Roma prendo il valore relativo all'area romana, pari ad c= 0,10

La Forza sismica totale è pari a

F = W * c

- Il sesto e il settimo step analizzano come la forza sismica agisce sui controventi e gli effetti che essa provoca , traslazione e rotazione orizzontali e verticali.

Mentre la sesta tabella permette di calcolare la forza sismica lungo x, la settima tabella quella lungo y.

- Gli effetti prodotti dalla forza sismica sulla struttura saranno:

lungo l'asse x 

traslazione

rotazione

lungo l'asse y

traslazione

rotazione

 

Questa quarta esercitazione consiste nel dimensionamento di un pilastro; che sia esso di legno, acciaio o calcestruzzo.

Ho preso in considerazione il pilastro maggiormente sollecitato a sforzo normale di un edificio di 4 piani; quindi, uno di quelli presenti a piano terra sui quali si scarica il peso dell'intera struttura sovrastante.

Ho ripreso la pianta della carpenteria utilizzata nella prima e nella terza esercitazione in modo da poter riutilizzare i valori dei carichi dei solai.

L'area di influenza del pilastro è quindi di 27 mq. (L1= 4,5 m ; L2= 6 m)

LEGNO

1) Dopo aver inserito i dati relativi alla grandezza del solaio ed aver trovato l'area di influenza del pilastro, calcolo il peso unitario della trave_p e della trave_s

trave= area della sezione (0,35 x 0,5) mq x peso specifico 5 KN/m3 = 0,88 KN/m

Posso calcolarmi così il carico dovuto al peso proprio delle travi 

q trave= (trave p x L1 x 1,3) + (trave s x L2 x 1,3) = 11,94 KN

2) Inserisco i valori dei carichi agenti sul solaio (carichi strutturali, carichi permanenti e carichi accidentali) per calcolare il valore complessivo del carico agente. 

q tot= (1,3 x qs + 1,5 x qp + 1,5 x qa) x A = 237,33 KN

3) infine calcolo lo sforzo di compressione N dato il numero dei piani

N= (q trave x q solaio) x n piani= 997 KN

 

Adesso posso ricavarmi l'area minima della sezione tale da evitare la rottura del materiale.

4) Inserisco tutte le caratteristiche relative al materiale 

-la resistenza a compressione (f_c0,k) 24MPa

-il coefficiente della durata di carico k_mod  0,8

-il coefficiente parziale di sicurezza γ_m. 1,45

e mi ricavo il valore della tensione ammissibile e dell'area minima:

f_c0d= f_c0,k x k_mod / γ_m. = 13,24 MPa

A min= 753 cm2

 

5) Sapendo che Il modulo di elasticità E = 8800 MPa, β =1 e l’altezza del pilastro è di 3 m, posso procedere con:

- il calcolo del valore massimo di snellezza λ_{max =} 80,95

- il valore minimo del raggio di inerzia ρ_min = 3,71 cm

- la grandezza della base b min = 12,84 cm, che ingegnerizzo scegliendo una b = 15 cm. 

- l’altezza minima h_min =   A_min / b = 50,20 cm, che ingegnerizzo scegliendo una h= 51 cm

6) Calcolo  l’area di progetto della sezione

A_design = b x h = 765 cm²

7) Verifico che A_design > A_min   

765 cm² > 753 cm²               SEZIONE VERIFICATA

8)  calcolo infine il momento d’inerzia di progetto

I_design = 14344 cm⁴

ACCIAIO

1)  Dopo aver inserito i dati relativi alla grandezza del solaio ed aver trovato l'area di influenza del pilastro, calcolo il peso unitario della trave p e della trave s

trave p = IPE 360 = 57,1 Kg/m = 0,57KN/m

trave s = IPE 160 = 15,8 Kg/m = 0,158 KN/m

Posso calcolarmi così il carico dovuto al peso proprio delle travi 

q trave= 4,57 KN

2) Inserisco i valori dei carichi agenti sul solaio (carichi strutturali, carichi permanenti e carichi accidentali) per calcolare il valore complessivo del carico agente. 

q tot= (1,3 x qs + 1,5 x qp + 1,5 x qa) x A = 269,24 KN

3) infine calcolo lo sforzo di compressione N dato il numero dei piani

N= (q trave x q solaio) x n piani= 1095 KN

 

 

Adesso posso ricavarmi l'area minima della sezione tale da evitare la rottura del materiale.

4) Inserisco tutte le caratteristiche relative al materiale 

- la tensione di snervamento (f_,yk) 275MPa

- il coefficiente parziale di sicurezza γ_m. 1,05

5) Posso quindi calcolare il valore della tensione ammissibile e dell'area minima

f_yd= f_c0,k / γ_m. = 261,90 MPa

A min= 41,8 cm²

 

5) Sapendo che Il modulo di elasticità E =  210000 N/mm² , β =1 e l’altezza del pilastro è di 3 m, posso procedere con:

- il calcolo del valore massimo di snellezza λ_{max =} 88,96

- il valore minimo del raggio di inerzia ρ_min = 3,37 cm

- calcolo il momento di inerzia minimo   I_min=  476 cm⁴

6)  Posso ora ingegnerizzare la sezione scegliendo un profilo HEA con valori maggiori rispetto a quelli minimi. Scelgo un profilo HEA 180

7) Verifico che A_design > A_min   

45,3 cm² > 41,8 cm²               SEZIONE VERIFICATA

8)  calcolo infine il valore della snellezza

 λ = 60,24

1)  Dopo aver inserito i dati relativi alla grandezza del solaio ed aver trovato l'area di influenza del pilastro, calcolo il peso unitario della trave p e della trave s

trave= area della sezione (0,3 x 0,55) mq x peso specifico 24 KN/m3 = 3,96 KN/m

Posso calcolarmi così il carico dovuto al peso proprio delle travi 

q trave= 54,05 KN

2) Inserisco i valori dei carichi agenti sul solaio (carichi strutturali, carichi permanenti e carichi accidentali) per calcolare il valore complessivo del carico agente. 

q tot= (1,3 x qs + 1,5 x qp + 1,5 x qa) x A = 314,71 KN

3) infine calcolo lo sforzo di compressione N dato il numero dei piani

N= (q trave x q solaio) x n piani= 1475 KN

Adesso posso ricavarmi l'area minima della sezione tale da evitare la rottura del materiale.

4) Inserisco la tensione di snervamento

(f_ck) 40 MPa

5) Calcolo i valori di 

- (f_cd) 22,7 MPa

- Amin =650,8 cm² 

- bmin = 25,5 cm

 

 

5) Sapendo che Il modulo di elasticità E =  210000 N/mm² , β =1 e l’altezza del pilastro è di 3 m, posso procedere con:

- il calcolo del valore massimo di snellezza λ_{max =} 95,62

- il valore minimo del raggio di inerzia ρ_min = 3,14cm

- la grandezza della base b min = 10,87 cm, che ingegnerizzo scegliendo una b = 40 cm

-  l’altezza minima h_min = 16,27 cm, che ingegnerizzo scegliendo una  h= 40 cm

6) Verifico che A_design > A_min   

45,3 cm² > 41,8 cm²               SEZIONE VERIFICATA

7) sapendo che:

- I_design= h x b^3 /12 = 213333 cm⁴

- I_max = b x h^3 /12 = 213333 cm4

-  Il modulo di resistenza a flessione W_max = b x h^2 / 6= 10666,67 cm³

- ilcarico distribuito sulla trave q =(1,3 x qs + 1,5 x qp + 1,5 x qa) x L2 = 69,94 KN/m

- il momento nell’estremo della trave M= q x L1^2 /12 = 118,02 KNm

8) calcolo la tensione massima

σ_max = 20,28 MPa

che risulta verificata poichè 

σ_max < f_cd     20,28 < 22,7  TENSIONE VERIFICATA

 

Questa esercitazione consiste nel dimensionamento e verifica di una trave a sbalzo, usando tre materiali differenti (legno, acciaio e cls).

Per comodità ho ripreso la stessa pianta di carpenteria della prima esercitazione dotandola di un aggetto di 3 m.

Il foglio excel da usare è composto di due parti di cui la prima uguale al foglio della prima esercitazione poichè riguarda i problemi legati allo Stato Limite Ultimo; mentre la seconda parte riguarda la deformabilità quindi lo Stato Limite d'Esercizio

SOLAIO IN LEGNO

Considero lo stesso solaio preso in considerazione nella prima esercitazione 

- Inizio a compilare la prima parte del foglio Excel con i valori dell'interasse, qs, qp, qa per ottenere quindi il qu = 37,797 Kn/m.

- Inserisco il valore dello sbalzo pari a 3 m per calcolare il momento massimo pari a Mmax = 170,08 KN*m

- inserisco ora i dati relativi al materiale ossia quello di un legno classe C24 (fmk = 24 N/mm² , Kmod = 0.8, γ m = 1.45) per ottenere un valore della tensione di progetto pari a f_dC = 13,24 N/mm² 

- scelgo una base di 35 cm ed ottengo una altezza di 46,33 cm che ingegnerizzo a 50 cm

- ora inizia la parte relativa allo SLE quindi inserisco un modulo elastico pari a E = 8000 N/mm² ed ottengo una Ix = 364583 cm⁴

- infine mi rendo conto che lo spostamento massimo v_max = 0,73 cm è verificato poichè il rapporto Ix/v_max >250

 

SOLAIO IN ACCIAIO

Come per il legno prendo in considerazione il pacchetto di solaio che avevo studiato per la prima esercitazione

- compilo la prima parte del foglio Excel come ho fatto per il legno per arrivare a trovare un valore di qu = 42,87 KN/m

- inserisco il valore della luce dello sbalzo e trovo un valore di Mmax = 192,95 KN*m

- per quanto riguarda il materiale ho scelto un acciaio di classe S235 che ha come caratteristiche una tensione fyk = 235 N/mm²

- trovato il valore di fd = 223,81 N/mm² calcoliamo il modulo di resistenza a flessione minimo uguale a Wx,min = 862,15 cm³

- consultando la tabella dei profilati IPE scelgo una IPE 360 sapendo che la resistenza a flessione deve essere più grande di quella trovata ( Wx = 904 cm³)

- Inserisco il valore di Ix ricavato dalla tabella Ix = 16270 cm⁴

- Dopo aver calcolato qe= 26,113 KN/m mi rendo conto che anche in questo caso il progetto è verificato poichè lo spostamento è uguale a v_max = 0,774 e quindi il rapporto  I_x/ v_max >250

SOLAIO IN CEMENTO ARMATO

- Compilo la prima parte del foglio Excel ed inserisco il valore dello sbalzo trovando così il valore del momento massimo Mmax= 225,54 KN*m

- Scelgo un acciaio di classe S450 ( fyk = 450 N/mm², fd = 391.30 N/mm² )

- Prendo un cls che abbia come tensione caratteristica fck = 60 N/mm² ed fcd = 34 N/mm²

- Prendo il valore di β=0.57 e di r=2.09 

- Considero una trave di base b = 30 cm e copriferro di 5 cm e trovo una altezza ingegnerizzata di H = 40 cm

- Il foglio excel verifica allora con i dati ottenuti se la trave presa in considerazione ha una tensione di progetto pari alla massima tensione esercitata in campata. La trave è verificata.

- Procediamo a calcolare la parte relativa allo SLE (qe = 33,6  KN/m)

- Anche questa volta la trave è verificata poichè  I_x/ v_max >250

Nella seconda esercitazione ho analizzato e dimensionato una struttura reticolare tridimensionale con l’ausilio del software SAP 2000 e di un foglio Excel.

Le aste reticolari sono sollecitate esclusivamente a sforzo normale (trazione e compressione).

Procedo con la descrizione dell’iter che, tramite SAP, mi ha permesso la modellazione della struttura reticolare e del calcolo degli sforzi sulle singole aste.

1) Apro un nuovo file cambiandone l’unità di misura in Kn,m,C scegliendo uno spazio di lavoro “Grid only”

2) Imposto la maglia strutturale con cubi di lato 3 m e dispongo 3 cubi lungo l'asse x ed y. Uso una griglia x=4 y=4 z=2

3) Inizio a modellare la mia struttura a base cubica collegando i vari vertici tra loro e controventando ogni singola faccia del cubo

4) Controllo se il mio modello non presenti aste duplicate cliccando su edit > edit points >merge duplicate

5) Correggo la tolleranza di 0,1 cliccando su edit > edit points > merge joints

6) Seleziono i quattro vertici inferiori e aggiungo delle cerniere tramite il comando assign > joint > restraints

7) Sblocco i nodi da sforzo flessionale selezionando la struttura e cliccando su Assign > Frame > Release partial fixity

8) Assegno il materiale alle aste che compongono la struttura tramite Frame > frame section > add ne property > pipe 

9) Imposto un nuovo schema di carichi cliccando su Define > Load pattern ed inserisco un nuovo parametro F coun un Self Weight Multiplier = 0

10) Seleziono esclusivamente i nodi superiori per caricarli aggiungendo una forza di -200 KN poichè diretta verso il basso. Clicco su Assigne > Joint loads > Forces

11) posso ora far partire l'analisi cliccando su Run analysis e selezionando esclusivamente la forza F come oggetto dell'indagine. Ottengo così la mia struttura deformata e posso controllare gli sforzi su di essa cliccando su Frame > Axiel force

12) Cliccando su  Display > Show tables posso controllare i dati dell'analisi spuntando Analisys Results e selezionando il valore F. Esportiamo adesso la tabella Element Forces - Frames in un file Excel per ottenere i dati utili al dimensionamento delle aste.

Per prima cosa elimino i dati ripetuti cliccando su Dati > rimuovi duplicati ed ordino gli sforzi dal più grande al più piccolo.

Adesso posso analizzare singolarmente gli sforzi di trazione (+) e gli sforzi di compressione (-)

TRAZIONE

- Nella prima colonna del foglio excel incollo gli sforzi normali delle aste per poi selezionare un acciaio di tipo S235 JR H con un valore di tensione di snervamento = 235 Mpa

- Aggingo il coefficiente y_s = 1,05 e ottengo un Fyd = 223,81 Mpa

- Ottenuta l'area minima di sezione procedo alla consultazione del profilario di aste a sezione circolare per il dimensionamento dei profili che avranno un'area maggiore rispetto a quella calcolata

COMPRESSIONE

- Per la compressione valgono gli stessi procedimenti descritti in precedenza ma con l'aggiunta del fenomeno di instabilità

- Aggiungo quindi il valore di E = 210000 Mpa e di beta = 1

- La lunghezza delle singole aste la ricavo facendo attenzione a quali di esse sono lati dei quadrati (3 m) e quali sono diagonali (4,24 m)

- Ottenuti i valori di Lambda, Rho min e I min procedo con il dimensionamento delle aste facendo attenzione che i valori del profilato siano superiori a quelli trovati

 

 

 

 

 

 

 

 

 

 

 

 

Nella seguente esercitazione cercherò di spiegare come dimensionare una trave portante di un solaio sollecitata a flessione. Ho analizzato tre differenti soluzioni (solaio in legno, acciaio e cls armato).

Di seguito il solaio da me ipotizzato: 

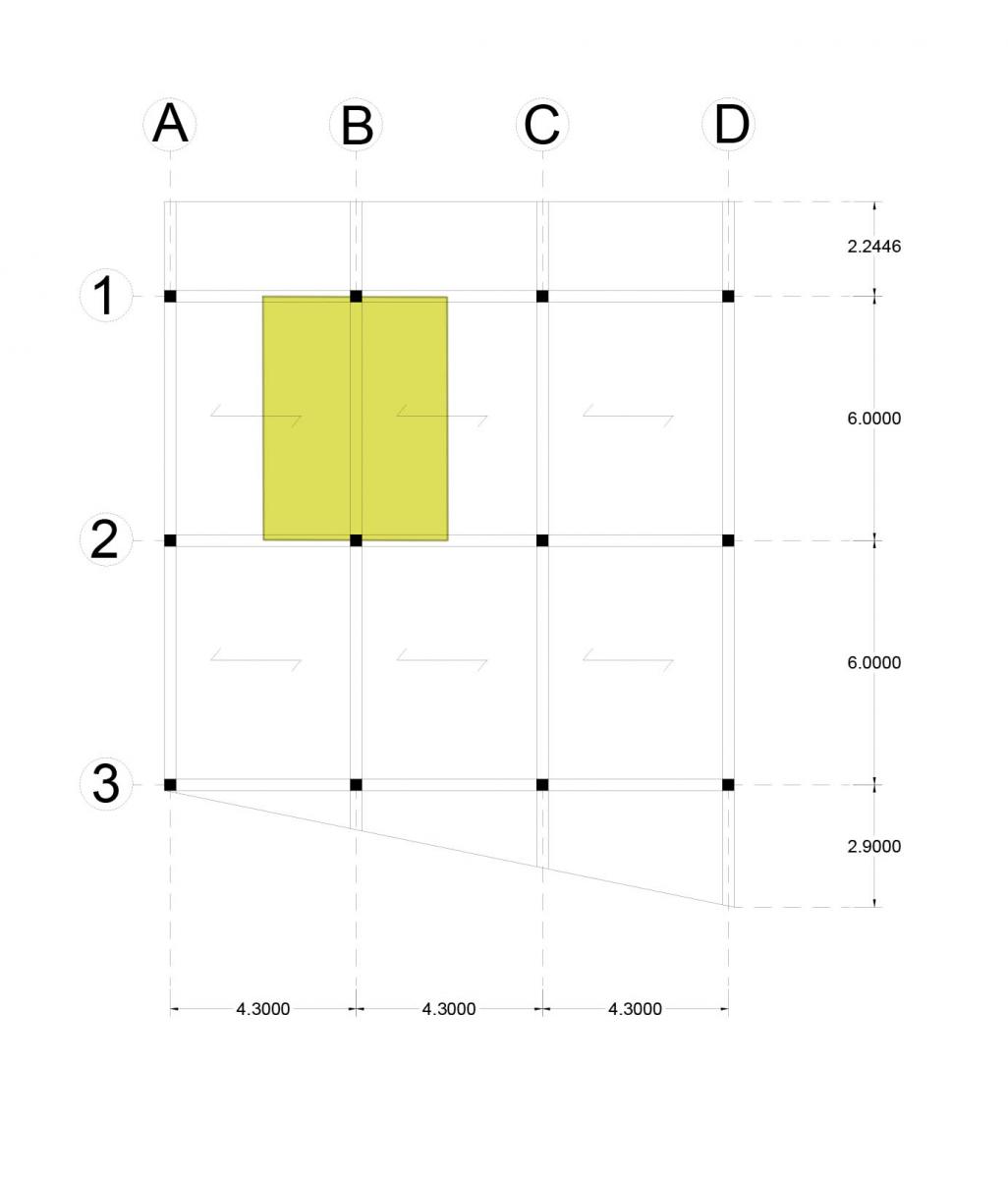
Ho analizzato la trave maggiormente sollecitata che porta una porzione di solaio di Area pari a

6 m x 4,3 m =25,8 m² nelle tre differenti casistiche.

 

SOLAIO IN LEGNO

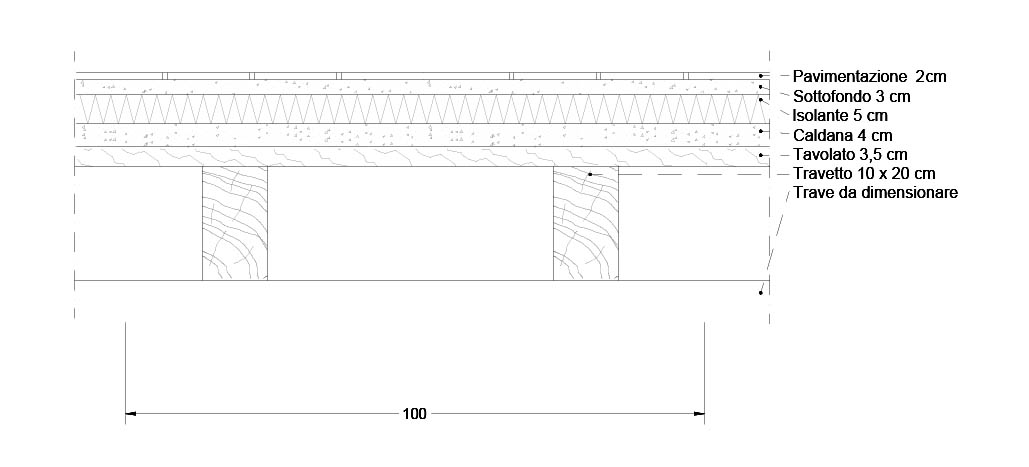
Il solaio preso in esame è composto da:

-Pavimentazione in Gres spessa 2 cm e peso specifico di 20 KN/m³

-Sottofondo in cls alleggerito spesso 3 cm e peso specifico di 18 KN/m³

-Strato isolante di 5 cm e peso specifico di 0,5 KN/m³

-Caldana spessa 4 cm e peso specifico di 25 kN/m³

-Tavolato di legno spesso 3,5 cm e peso specifico di 6 kN/m³

-Travetti di legno 10 x 20 cm e peso specifico di 6 kN/m³

Per dimensionare la trave devo fare una analisi dei carichi considerando i carichi strutturali, quelli permanenti e quelli accidentali che andranno moltiplicati per i rispettivi coefficienti di riduzione.

Carichi strutturali (q_s):

-2 travetti: 2 x (0,05 x 0,2) m³/m² x 6  kN/m³ = 0,24 kN/m²

-Tavolato: 0,035 m³/m² x 6 kN/m³ = 0,21 kN/m²

Q_stot =  0, 45 kN/m²

Carichi permanenti (q_p):

-Pavimentazione in Gres: 0,02 m³/m² x 20 kN/m³ = 0,4 kN/m²

-Sottofondo in cls alleggerito: 0,03 m³/m² x 18 kN/m³ = 0,54 kN/m²

-Isolante: 0,05 m³/m² x 0,5 kN/m³ = 0,025 kN/m²

-Caldana: 0,04 m³/m² x 25 kN/m³ = 1 kN/m²

A questi carichi aggiungiamo il contributo dei Tramezzi pari a 1 kN/m² e degli impianti pari a 0,5 kN/m²

Q_ptot =  3,465 kN/m^2​

Carichi accidentali (q_a):

Il carico accidentale è dato da normativa e si riferisce ad una ipotesi di uso residenziale dell’edificio. Prendiamo un valore di 2 kN/m²

​Q_a =  2 kN/m²             

 Procediamo a tabellare i valori ottenuti sul foglio Excel prendendo in considerazione per la trave un legno lamellare GL24 h con resistenza a flessione pari a 24 Mpa, fissando una base di 35 cm

Analizzando i dati ricavati dal foglio Excel ci rendiamo conto di dover adottare una trave di h = 50 cm e quindi sezione 35 x 50 cm

Procediamo a verificare la fattibilità di tale progetto calcolando il peso proprio della trave 

-Trave in legno lamellare ( Area = 1750 cm², Peso specifico = 3,8 kN/m³ ): 0,175 m³/m² x 3,8 kN/m³ = 0,665 kN/m²

Q_tot =  37,76 + (1,3 x 0,665) = 38,62 kN/m

L’altezza minima trovata è inferiore a quella considerata di 50 cm quindi la trave risulta verificata

 

SOLAIO IN ACCIAIO

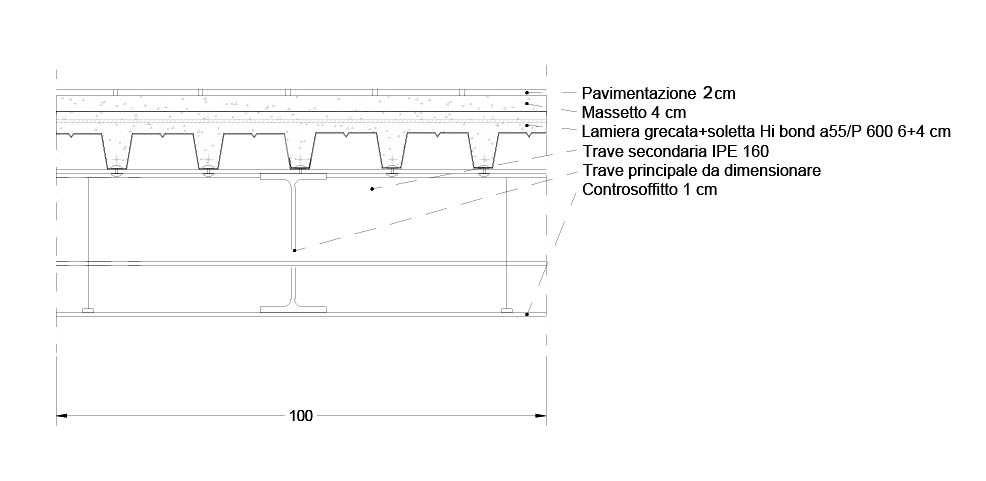Il solaio preso in esame è composto da:

-Pavimentazione in Gres spessa 2 cm e peso specifico di 20  kN/m³

-Massetto in cls alleggerito spesso 4 cm e peso specifico di 18  kN/m³

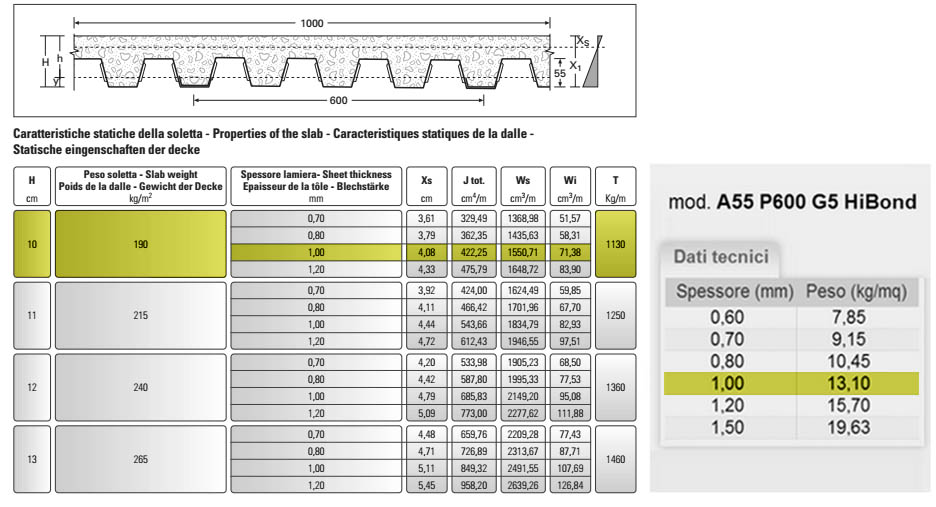
-Lamiera grecata + soletta Hi Bond a55/p 600 di 10 cm (6 + 4) e peso specifico rispettivamente di 13 kN/m³ e 19 kN/m³

-Travetto IPE 160 di Area 20,1 cm² e peso specifico di 78,5 kN/m³

-Controsoffitto in cartongesso spesso 1 cm  e peso specifico di 13 kN/m³

Carichi strutturali (q_s):

-IPE 160: 0,00201 m³/m² x 78,5  kN/m³ = 0,157 kN/m²

-Soletta in cls: 0,1 m³/m² x 19 kN/m³ = 1,9  kN/m²

-Lamiera grecata: 0,001 m³/m² x 13 kN/m³ = 0,13 kN/m²

Q_stot =  2,187 kN/m​²

Carichi permanenti (q_p):

-Pavimentazione in Gres: 0,02 m³/m² x 20 kN/m³ = 0,4 kN/m²

-Massetto in cls alleggerito: 0,04 m³/m² x 18 kN/m³ = 0,72 kN/m²

-Controsoffitto: 0,01 m³/m² x 13 kN/m³ = 0,13 kN/m²

A questi carichi aggiungiamo il contributo dei Tramezzi pari a 1 kN/m² e degli impianti pari a 0,5 kN/m²

Q_ptot =  2,75 kN/m²

Carichi accidentali (q_a):

Q_a =  2 kN/m²

Procediamo a tabellare i dati nel foglio Excel scegliendo un tipo di acciaio Fe 430/S275

Avendo ottenuto un W_x pari a 736,46 cm³ si può adottare un profilo IPE 360 con modulo di resistenza immediatamente successivo e pari a 904 cm²

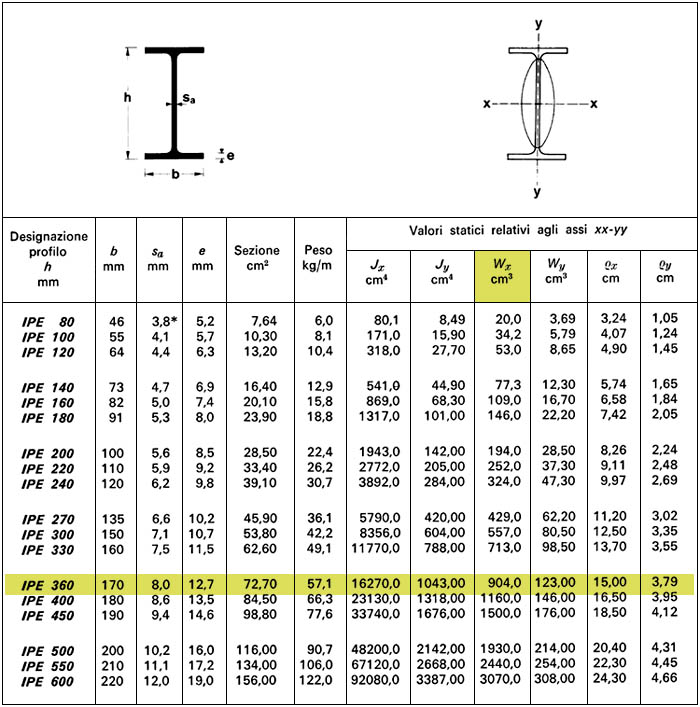
Si può adesso calcolare il peso proprio della trave, per aggiungerlo ai carichi agenti sulla struttura, opportunamente moltiplicato per il coefficiente di sicurezza ad 1,3

-Trave IPE 360 (Area = 72,7 cm²): 0,00727m³/m² x 78,5 kN/m³ = 0,571 kN/m²

Q_tot =  44,41 + (1,3 x 0,571) = 45,15 kN/m

Il nuovo W_x è sempre al di sotto dei 904 cm³ del modulo di resistenza dell’IPE 360, quindi tale profilo risulta verificato.

 

SOLAIO IN CLS ARMATO

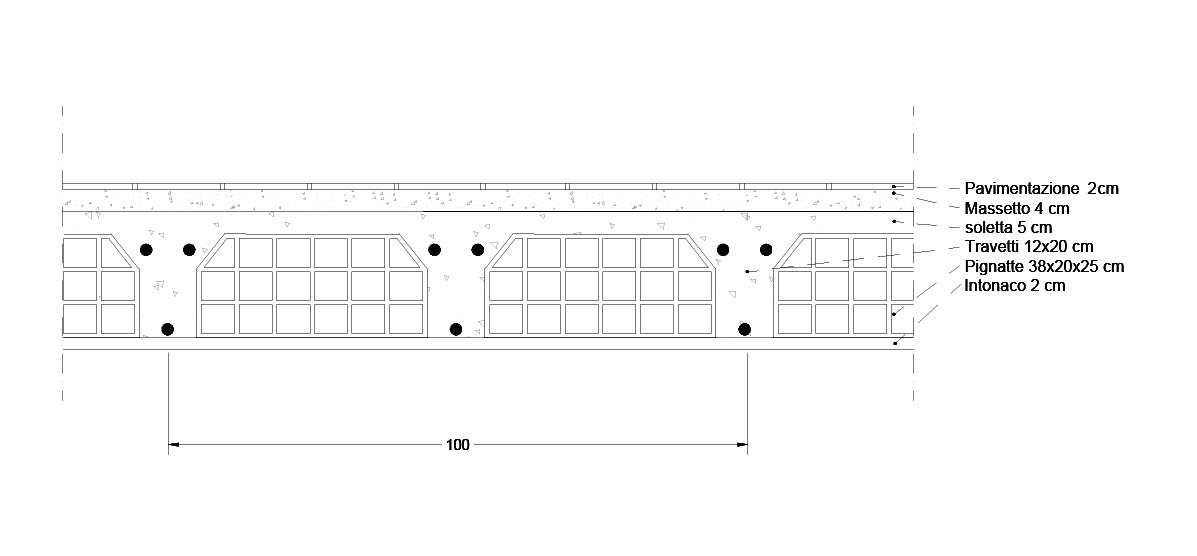
Il solaio preso in esame è composto da:

-Pavimentazione in Gres spessa 2 cm e peso specifico di 20  kN/m³

-Massetto in cls alleggerito spesso 4 cm e peso specifico di 18  kN/m³

-Soletta in cls spessa 5 cm e peso specifico 25 kN/m³

^--Pignatte 38x20x25 cm dal peso di 0,096 kN l'una

^-Travetti 12x20 cm con un peso specifico di 25 kN/m³ 

^-Intonaco spesso 2 cm con peso specifico di 18 kN/m³ 

Carichi strutturali (q_s):

-2 travetti : 2 x (0,012 x 0,2 x 1) m³/m² x 25  kN/m³ = 1,2 kN/m²

-Soletta in cls armato: 0,05 m³/m² x 25 kN/m³ = 1,25  kN/m²

Per calcolare l'incidenza delle pignatte si deve prima calcolare quante ce ne sono in un m². In questo caso si avranno due file di pignatte nel senso dei travetti, ciascuna composta da 4 elementi, per un totale di 8 pignatte al m². 

-Pignatte: 8 m^-2 x 0,096 kN = 0,768 kN/m²

Q_stot =  3,218 kN/m​²

Carichi permanenti (q_p):

-Pavimentazione in Gres: 0,02 m³/m² x 20 kN/m³ = 0,4 kN/m²

-Massetto in cls alleggerito: 0,04 m³/m² x 18 kN/m³ = 0,72 kN/m²

-Intonaco: 0,02 m³/m² x 18 kN/m³ = 0,36 kN/m²

A questi carichi aggiungiamo il contributo dei Tramezzi pari a 1 kN/m² e degli impianti pari a 0,5 kN/m²

Q_ptot =  2,98 kN/m​²

Carichi accidentali (q_a):

Q_a =  2 kN/m​²

Procediamo a tabellare i dati nel foglio Excel scegliendo, per la trave da progettare, dei ferri di armatura B450C (fyk = 450 MPa) ed un calcestruzzo ordinario C35/45 (fck=35MPa, Rck=45Mpa), la base della trave di 30 cm e un copriferro di 5 cm.

Osservando i dati ci rendiamo conto che l’h minima richiesta è di 50,28 cm quindi possiamo optare per una trave di sezione 30 x 55 cm.

Calcoliamo il peso della trave 

-Trave: (0,30 x 0,55 x 1) m³/m² x 25 kN/m³ = 4,125 kN/m²

Q_tot =  50,11 + (1,3 x 4,125) = 55,47 kN/m

La sezione risulta verificata