ES.5 Ripartizione forze sismiche

La quinta esercitazione consiste nel calcolo della ripartizione di una forza orizzontale agente su una struttura (constituita da telai Shear-Type) in cemento armato utilizzando il metodo delle rigidezze.

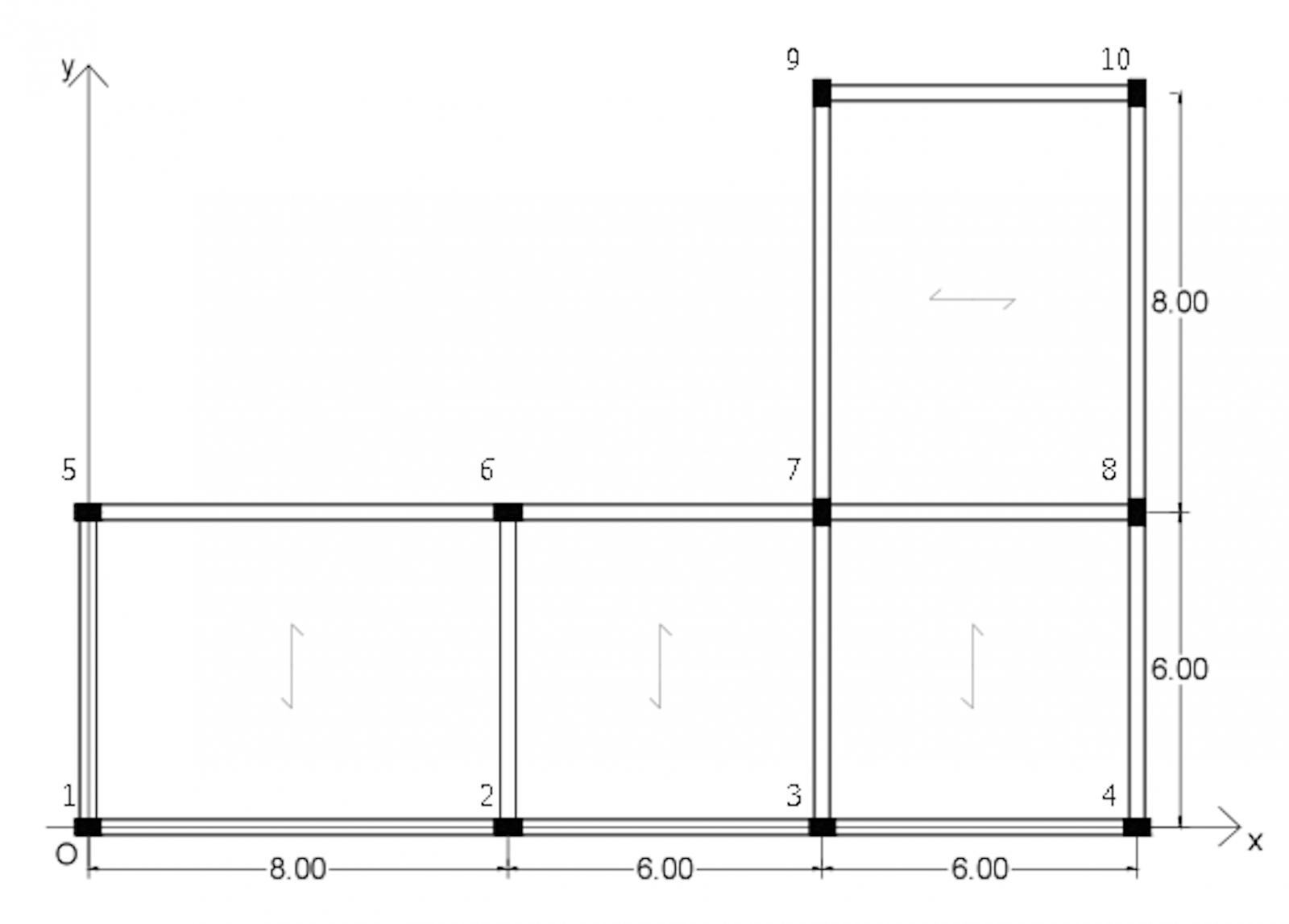
La struttura presa in esame utilizza dei pilastri (0.4 cm x 0.3 cm) cosi composta:

• telaio 1v    pilastri 1 e 5
• telaio 2v    pilastri 2 e 6
• telaio 3v    pilastri 3 - 7 -9
• telaio 4v    pilastri 4 - 8 - 10
• telaio 1o    pilastri 1 - 2 - 3 - 4 
• telaio 2o    pilastri 5 - 6 - 7 - 8
• telaio 3o    pilastri 9 - 10

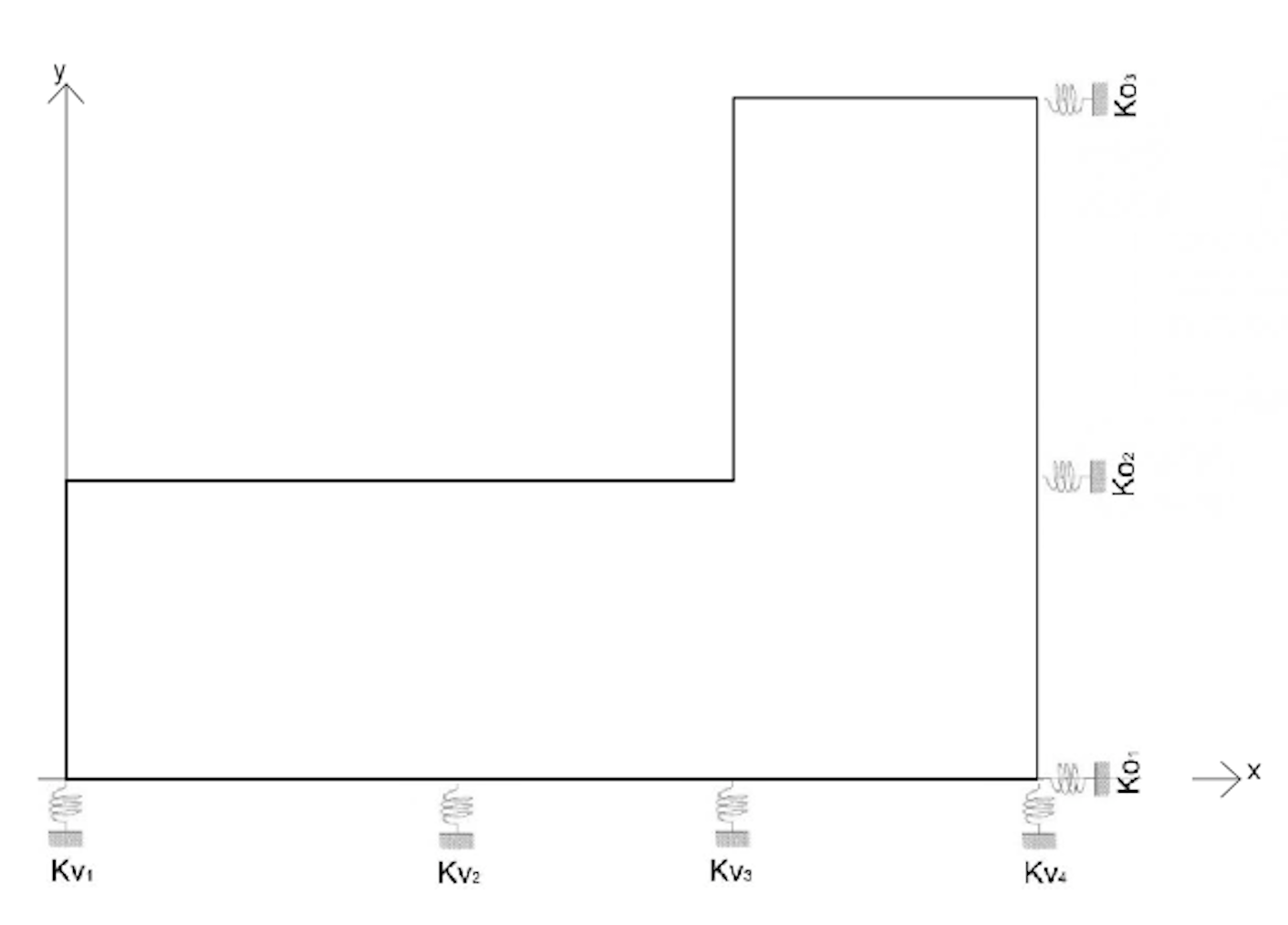
Rappresentiamo i controventi con delle molle dal momento che sono dei vincoli cedevoli elasticamente, rappresentano cioè le forze che i telai oppongono quando l'impalcato viene spostato. 

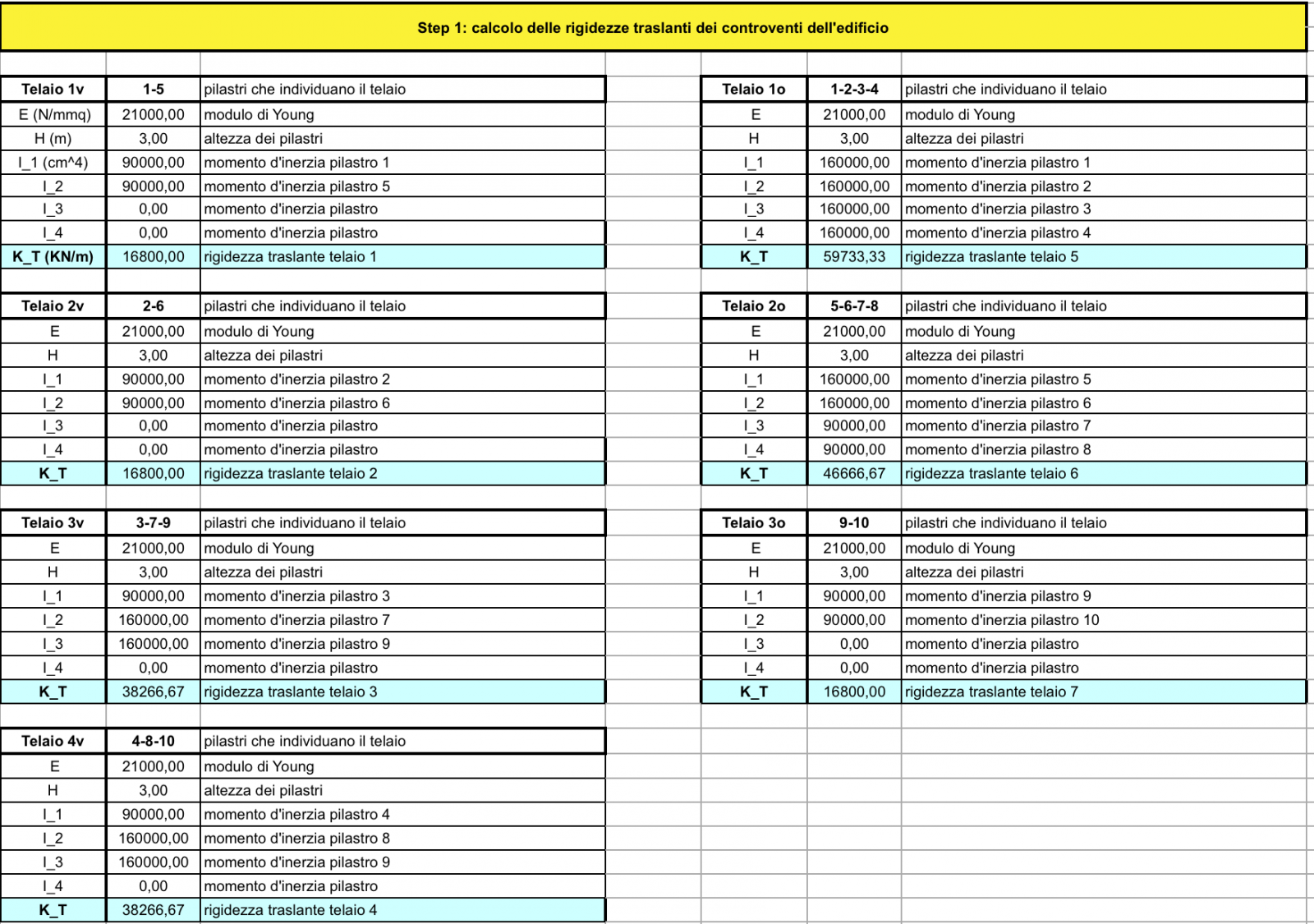
STEP 1 

Per calcolare le rigidezze dei controventi, iniziamo con l’inserire i dati relativi ai pilastri e i loro momenti d’inerzia: quello minore pari a 90000cm⁴ e momento di inerzia maggiore 160000 cm⁴. 

Sapendo che la rigidezza di ogni pilastro del telaio Shear-Type è data dalla formula: K= 12EI / h^3.

Nel caso in cui un telaio è costituito da più pilastri, la rigidezza k è definita: K= 12E / h³(I₁+I₂+...+I_n).

STEP 2

In questa tabella vengono inseriti i valori delle rigidezze di ogni controvento e le relative distanze dall’origine del sistema.

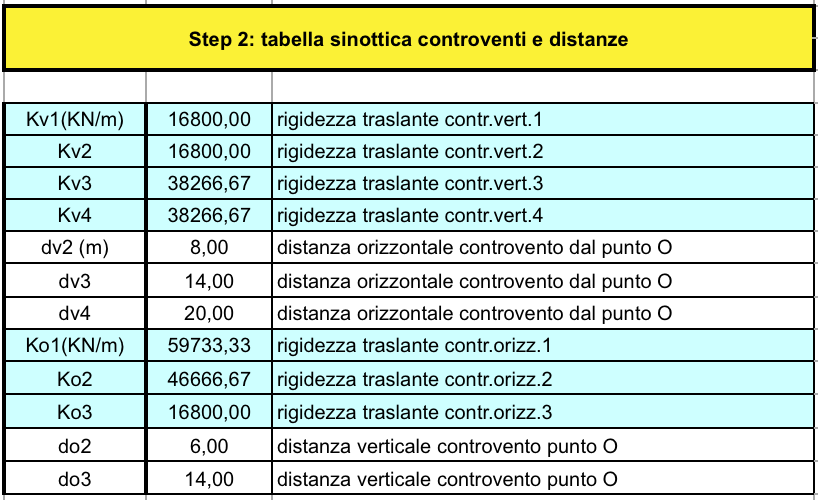
STEP 3

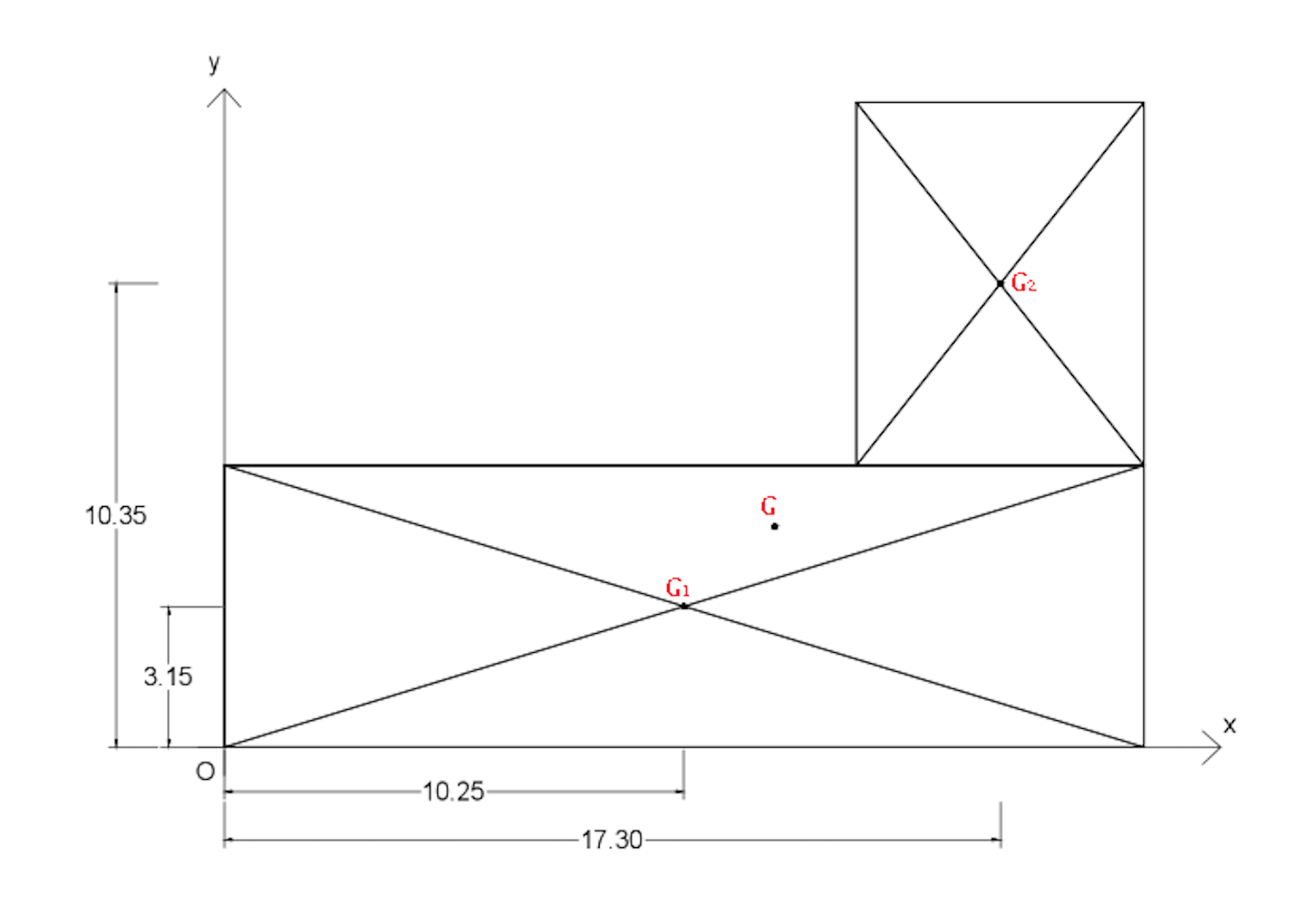
a questo punto possiamo calcolare il centro di massa (che nel caso di un impalcato con densità di massa uniforme, coincide con il centro di area). 

Per calcolare il centro di massa occorre suddividere l’impalcato in due figure geometriche elementari, calcolare le aree e le distanze del loro centro geometrico. 

Il centro di massa sarà quel punto in cui verrà applicata la forza sismica. 

(X_g= A₁*X_g1 + +A₂*X_g2 / A_{tot ;} Y_g= A₁*Y_g1 + A₂*Y_g2 / A_tot).

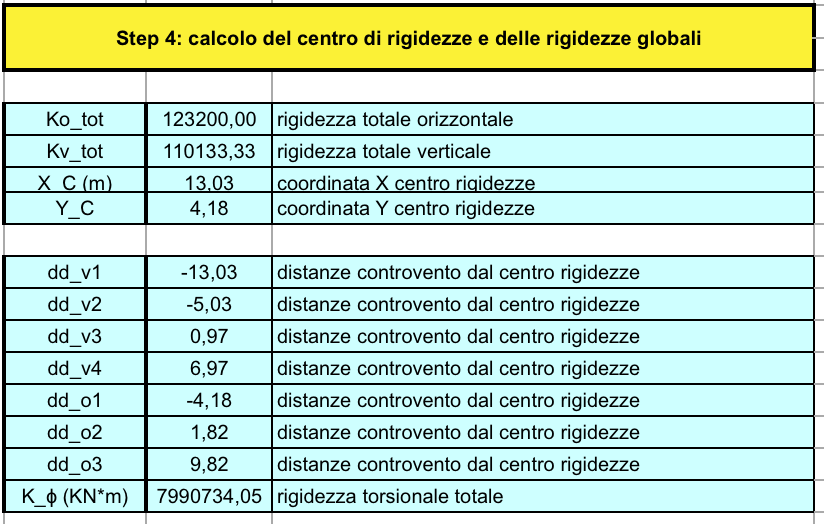
STEP 4

il foglio excel calcola il totale delle rigidezze sia orizzontale che verticale, e ricava le coordinate del centro delle rigidezze: 

X_c= K_v1*d_v1 + K_v2*d_v2 + ... + K_vn*d_vn/ K_vtot 

Y_c= K_o1*d_o1 + K_o2*d_o2 + ...... + K_on*d_on/ K_otot

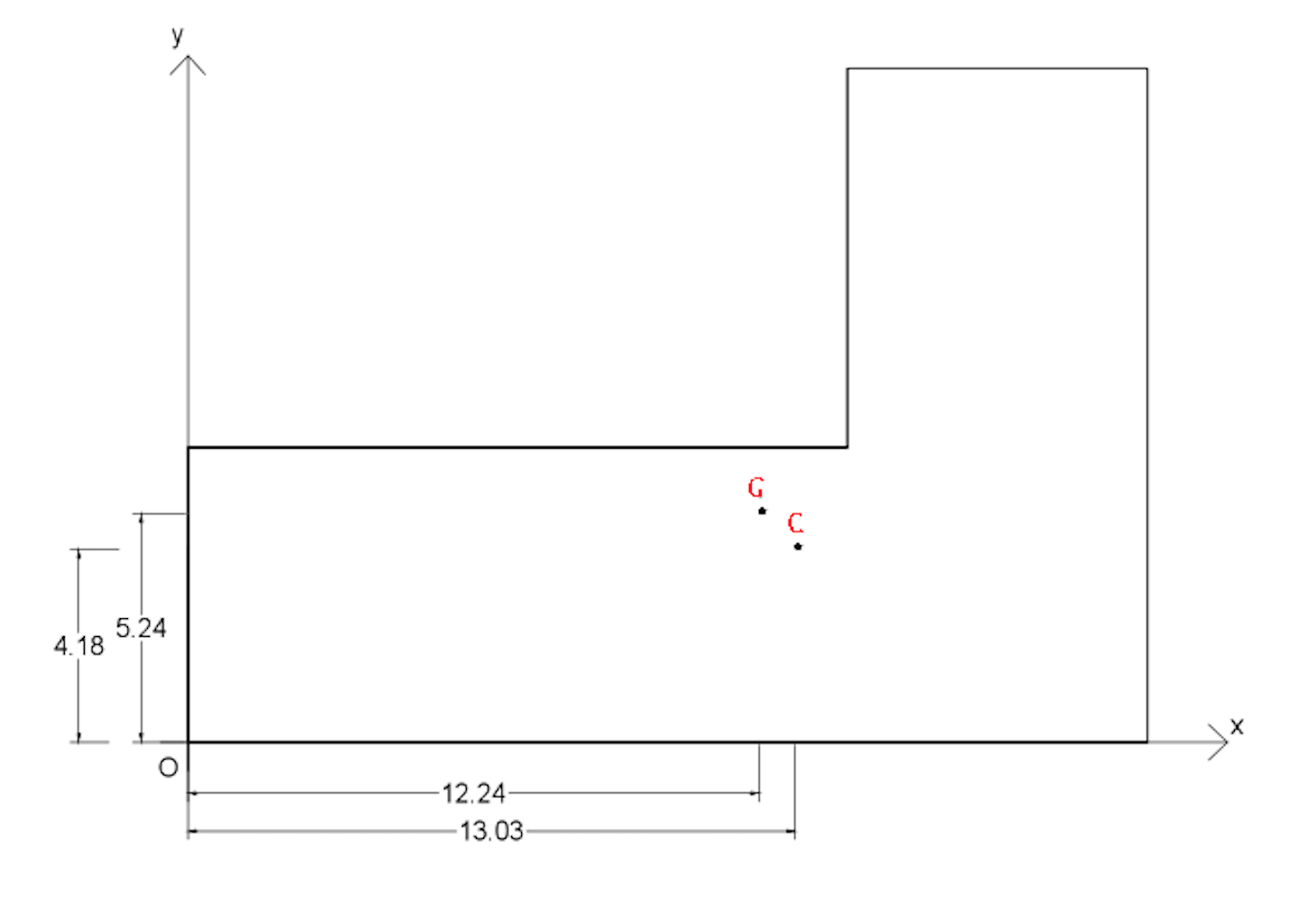
il centro di massa ed il centro delle rigidezze non coincidono. A questo punto è opportuno fare delle cosiderazioni:

1. la forza sismica viene applicata nel centro di massa.
2. se il centro di massa si trova sullo stesso asse del centro delle rigidezze, l’impalcato traslerebbe soltanto (verticalmente o orizzontalmente)
3. poiché il centro di massa si trova su un asse differente da quello del centro delle rigidezze, l’impalcato oltre a traslare subisce anche una rotazione. Questo perché la distanza tra i due centri diventa il braccio della forza F, e si  genera un momento.

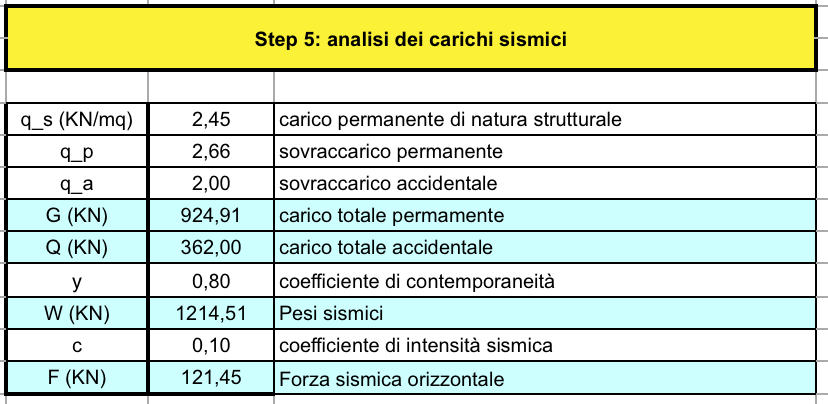
STEP 5

Passiamo ora ad analizzare i carichi che agiscono sull’impalcato

• qs (carichi strutturali) 
• qp (carichi permanenti)
• qa (carichi accidentali)

Sapendo che G= (qs + qp) x Atot

Possiamo calcolare il peso sismico W utilizzando il coefficiente di  contemporaneità (ψ)      W= G +  ψ2j x Q

Ora è possibile calcolare la forza agente che verrà applicata al centro di massa:

F= W x c      (c= coefficiente di intensità sismica)

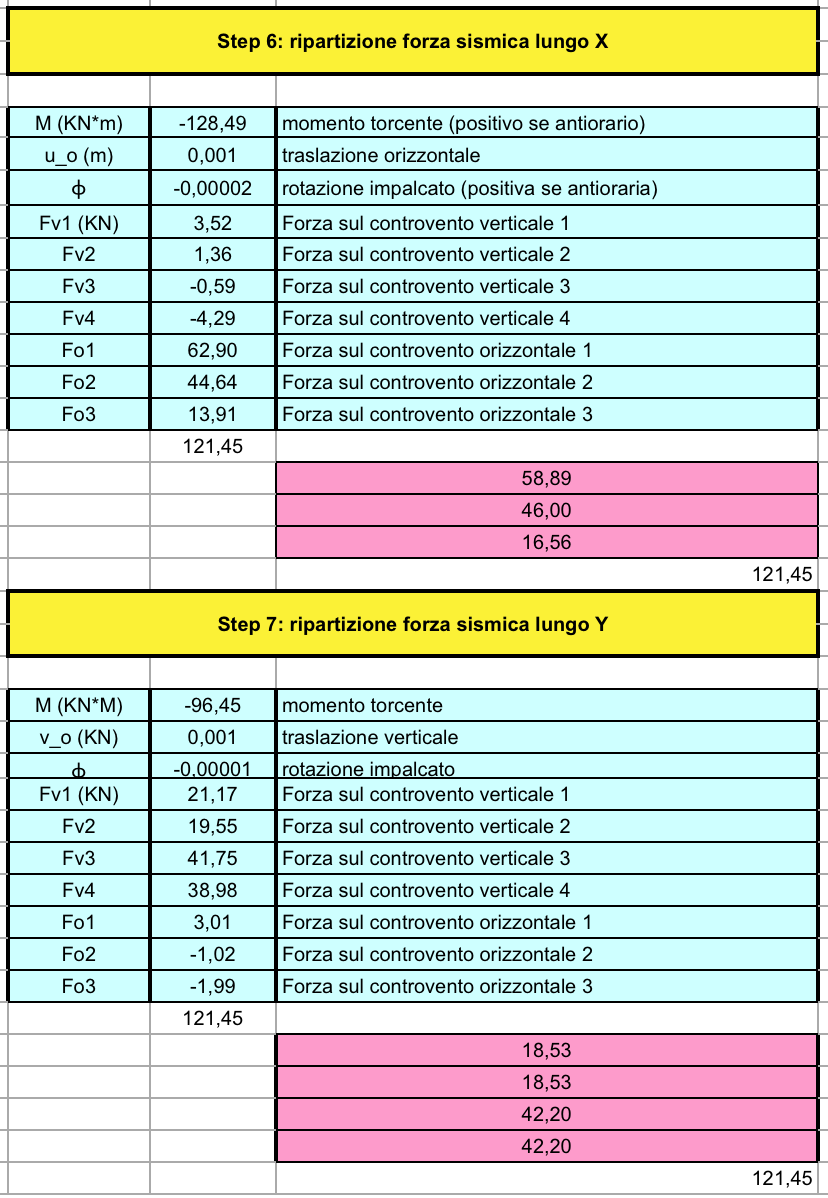
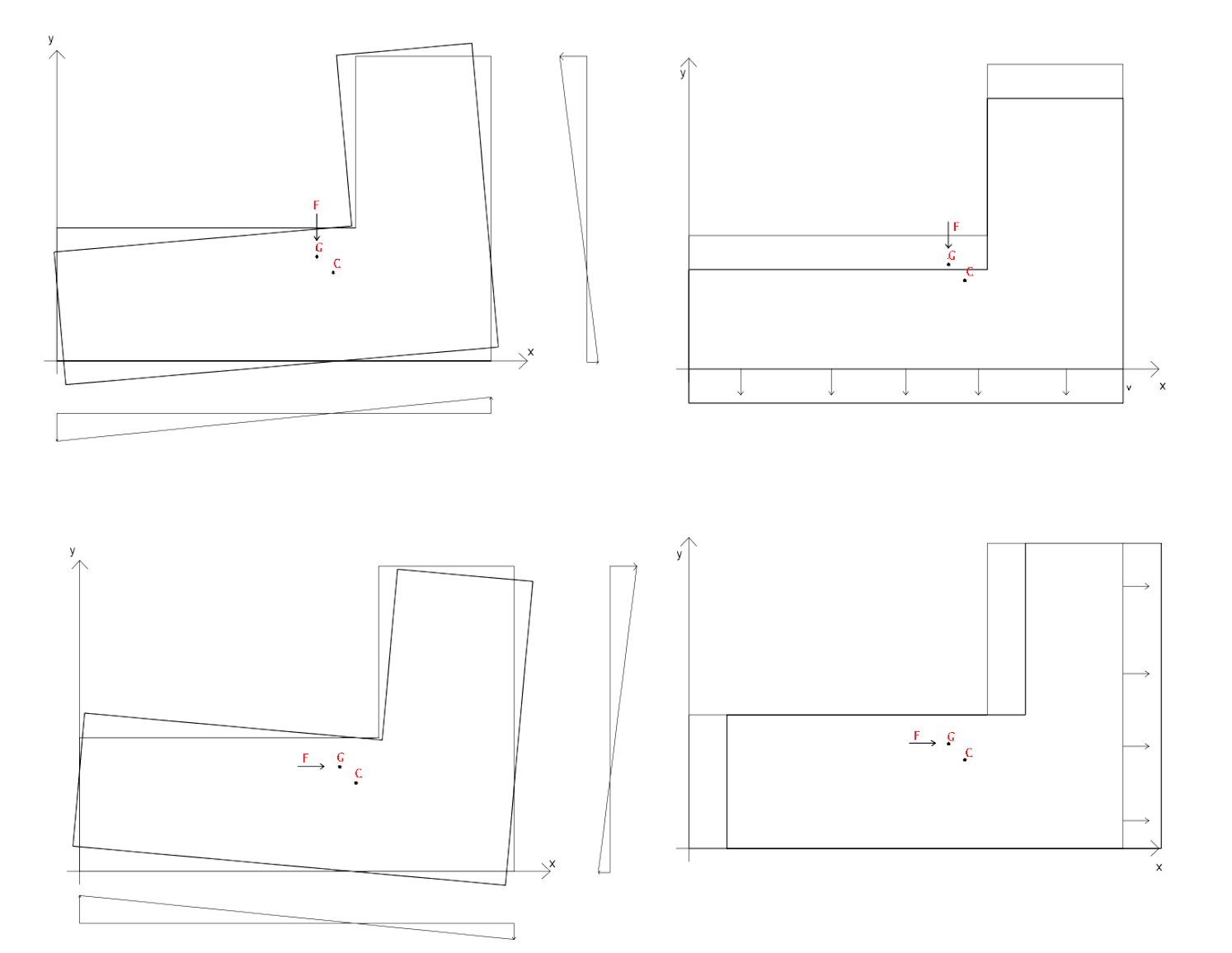
STEP 6 e 7

Si nota come la forza sismica si ripartisce sui controvento sia in direzione x che in direzione y.

Successivamente quantifica la cinematica dell’impalcato:

traslazione orizzontale    u = F/k_{o_tot} 

traslazione verticale      v = F/k_{v_tot}

rotazione      φ = W/kφ .