blog di ant.scirocchi

La quinta esercitazione consiste nel calcolo della ripartizione di una forza orizzontale agente su una struttura (constituita da telai Shear-Type) in cemento armato utilizzando il metodo delle rigidezze.

La struttura presa in esame utilizza dei pilastri (0.4 cm x 0.3 cm) cosi composta:

• telaio 1v    pilastri 1 e 5
• telaio 2v    pilastri 2 e 6
• telaio 3v    pilastri 3 - 7 -9
• telaio 4v    pilastri 4 - 8 - 10
• telaio 1o    pilastri 1 - 2 - 3 - 4 
• telaio 2o    pilastri 5 - 6 - 7 - 8
• telaio 3o    pilastri 9 - 10

Rappresentiamo i controventi con delle molle dal momento che sono dei vincoli cedevoli elasticamente, rappresentano cioè le forze che i telai oppongono quando l'impalcato viene spostato. 

STEP 1 

Per calcolare le rigidezze dei controventi, iniziamo con l’inserire i dati relativi ai pilastri e i loro momenti d’inerzia: quello minore pari a 90000cm⁴ e momento di inerzia maggiore 160000 cm⁴. 

Sapendo che la rigidezza di ogni pilastro del telaio Shear-Type è data dalla formula: K= 12EI / h^3.

Nel caso in cui un telaio è costituito da più pilastri, la rigidezza k è definita: K= 12E / h³(I₁+I₂+...+I_n).

STEP 2

In questa tabella vengono inseriti i valori delle rigidezze di ogni controvento e le relative distanze dall’origine del sistema.

STEP 3

a questo punto possiamo calcolare il centro di massa (che nel caso di un impalcato con densità di massa uniforme, coincide con il centro di area). 

Per calcolare il centro di massa occorre suddividere l’impalcato in due figure geometriche elementari, calcolare le aree e le distanze del loro centro geometrico. 

Il centro di massa sarà quel punto in cui verrà applicata la forza sismica. 

(X_g= A₁*X_g1 + +A₂*X_g2 / A_{tot ;} Y_g= A₁*Y_g1 + A₂*Y_g2 / A_tot).

STEP 4

il foglio excel calcola il totale delle rigidezze sia orizzontale che verticale, e ricava le coordinate del centro delle rigidezze: 

X_c= K_v1*d_v1 + K_v2*d_v2 + ... + K_vn*d_vn/ K_vtot 

Y_c= K_o1*d_o1 + K_o2*d_o2 + ...... + K_on*d_on/ K_otot

il centro di massa ed il centro delle rigidezze non coincidono. A questo punto è opportuno fare delle cosiderazioni:

1. la forza sismica viene applicata nel centro di massa.
2. se il centro di massa si trova sullo stesso asse del centro delle rigidezze, l’impalcato traslerebbe soltanto (verticalmente o orizzontalmente)
3. poiché il centro di massa si trova su un asse differente da quello del centro delle rigidezze, l’impalcato oltre a traslare subisce anche una rotazione. Questo perché la distanza tra i due centri diventa il braccio della forza F, e si  genera un momento.

STEP 5

Passiamo ora ad analizzare i carichi che agiscono sull’impalcato

• qs (carichi strutturali) 
• qp (carichi permanenti)
• qa (carichi accidentali)

Sapendo che G= (qs + qp) x Atot

Possiamo calcolare il peso sismico W utilizzando il coefficiente di  contemporaneità (ψ)      W= G +  ψ2j x Q

Ora è possibile calcolare la forza agente che verrà applicata al centro di massa:

F= W x c      (c= coefficiente di intensità sismica)

STEP 6 e 7

Si nota come la forza sismica si ripartisce sui controvento sia in direzione x che in direzione y.

Successivamente quantifica la cinematica dell’impalcato:

traslazione orizzontale    u = F/k_{o_tot} 

traslazione verticale      v = F/k_{v_tot}

rotazione      φ = W/kφ .

La quarta esercitazione consiste nel dimensionamento della sezione di un pilastro, ipotizzandolo nelle tre diverse tecnologie: Legno, acciaio e calcestruzzo armato. Il pilastro che viene preso in considerazione, in un edificio di 4 piani, è sicuramente uno di quelli presenti al piano terra, poiché su di lui vengono trasmessi tutti i carichi dei piani superiori ed è quindi quello maggiormente sollecitato a sforzo normale ( compressione). 

Dalla pianta di carpenteria, il pilastro che viene maggiormente sollecitato è quello la cui area di influenza è di 24 mq. (L1= 4 m ; L2= 6 m)

LEGNO

parte 1 e 2 Nelle prime due parti del nuovo foglio excel, si inizia l’analisi calcolando l’area di influenza (mq) del pilastro, poi utilizzando i carichi dei solai dell’esercitazione 1 e 3 

http://design.rootiers.it/strutture/node/1685    -    http://design.rootiers.it/strutture/node/1785

posso calcolare lo sforzo normale N di compressione agente sul pilastro stesso (KN). 

step 1 calcolo il peso unitario della trave p e della trave s

trave= area della sezione (0,3 x 0,5) mq x peso specifico 5 KN/m3 = 0,75 KN/m

step 2 calcolo il carico dovuto al peso proprio delle travi

q trave= (trave p x L1 x 1,3) + (trave s x L2 x 1,3) = 9,75 KN

step 3 Inserisco i valori dei carichi agenti sul solaio (carichi strutturali, carichi permanenti e carichi accidentali) e posso calcolare il valore complessivo del carico agente. 

q tot= (1,3 x qs + 1,5 x qp + 1,5 x qa) x A = 205,49 KN

step 4 ora posso calcolare lo sforzo di compressione N

N= (q trave x q solaio) x n piani= 861 KN

parte 3 e 4 Le ultime due parti del foglio excel permettono di ricavare l’area minima che deve avere la sezione in modo tale che il materiale non arrivi a rottura (Amin) e poi di ricavare il momento di inerzia minimo di progetto (Imin)

step 5 inserisco tutte le caratteristiche del materiale: la resistenza a compressione (f_c0,k) 24MPa, il coefficiente della durata di carico k_mod  0,8 e il coefficiente parziale di sicurezza γ_m. 1,45

Posso quindi calcolare il valore della tensione ammissibile

f_c0d= f_c0,k x k_mod / γ_m. = 13,24 MPa

A min= 650,2 cm2

step 6 Sapendo che Il modulo di elasticità E = 8800 MPa, β =1 e l’altezza del pilastro è di 2,75 m, posso procedere con:

1. il calcolo del valore massimo di snellezza λ_{max =} 80,95
2. il valore minimo del raggio di inerzia ρ_min = 3,40 cm
3. calcolo la grandezza della base b min = 2 x rad3 x ρ_min = 11,77 cm, che ingegnerizzo scegliendo una b = 13 cm. 
4. calcola l’altezza minima h_min =   A_min / b = 50,02 cm —>  h= 51 cm

step 7 calcolo l’area di progetto della sezione A_design = b x h = 663 cm2

step 8 devo verificare che A_design > A_min   663 > 650,2  SEZIONE VERIFICATA

step 9 calcolo infine il momento d’inerzia di progetto I_design = h x b3 / 12 = 9337 cm4

ACCIAIO

parte 1 e 2 Nelle prime due parti del nuovo foglio excel, si inizia l’analisi calcolando l’area di influenza (mq) del pilastro, poi utilizzando i carichi dei solai dell’esercitazione 1 e 3. 

posso calcolare lo sforzo normale N di compressione agente sul pilastro stesso (KN). 

step 1 calcolo il peso unitario della trave p e della trave s

trave p = IPE 330 = 49,1 Kg/m = 0,49 KN/m

trave s = IPE 200 = 22,4 Kg/m = 0,224 KN/m

step 2 calcolo il carico dovuto al peso proprio delle travi

q trave= (trave p x L1 x 1,3) + (trave s x L2 x 1,3) = 4,30 KN

step 3 Inserisco i valori dei carichi agenti sul solaio (carichi strutturali, carichi permanenti e carichi accidentali) e posso calcolare il valore complessivo del carico agente. 

q tot= (1,3 x qs + 1,5 x qp + 1,5 x qa) x A = 208,78 KN

step 4 ora posso calcolare lo sforzo di compressione N

N= (q trave x q solaio) x n piani= 852 KN

parte 3 e 4 Le ultime due parti del foglio excel permettono di ricavare l’area minima che deve avere la sezione in modo tale che il materiale non arrivi a rottura (Amin) e poi di ricavare il momento di inerzia minimo di progetto (Imin)

step 5 inserisco tutte le caratteristiche del materiale: la tensione di snervamento (f_,yk) 275MPa e il coefficiente parziale di sicurezza γ_m. 1,05

Posso quindi calcolare il valore della tensione ammissibile

f_yd= f_c0,k / γ_m. = 261,90 MPa

A min= 32,5 cm2

step 6 Sapendo che Il modulo di elasticità E = 210000 N/mm2, β =1 e l’altezza del pilastro è di 2,75 m, posso procedere con:

1. il calcolo del valore massimo di snellezza λ_{max =} 88,96
2. il valore minimo del raggio di inerzia ρ_min = 3,09 cm
3. calcolo il momento di inerzia minimo   I_min= A x (ρ_min )^2 = 311 cm4

step 7 Posso ora ingegnerizzare la sezione scegliendo un profilo HEA con valori maggiori rispetto a quelli minimi. Scelgo un profilo HEA 160

step 8 devo verificare che A_design > A_min   38,8 > 32,5  SEZIONE VERIFICATA

step 9 calcolo infine il valore della snellezza  λ = 69,1

CALCESTRUZZO

parte 1 e 2 Nelle prime due parti del nuovo foglio excel, si inizia l’analisi calcolando l’area di influenza (mq) del pilastro, poi utilizzando i carichi dei solai dell’esercitazione 1 e 3 

posso calcolare lo sforzo normale N di compressione agente sul pilastro stesso (KN). 

step 1 calcolo il peso unitario della trave e della trave s

trave= area della sezione (0,3 x 0,4) mq x peso specifico 24 KN/m3 = 2,88 KN/m

step 2 calcolo il carico dovuto al peso proprio delle travi

q trave= (trave p x L1 x 1,3) + (trave s x L2 x 1,3) = 37,44 KN

step 3 Inserisco i valori dei carichi agenti sul solaio (carichi strutturali, carichi permanenti e carichi accidentali) e posso calcolare il valore complessivo del carico agente. 

q tot= (1,3 x qs + 1,5 x qp + 1,5 x qa) x A = 262,9 KN

step 4 ora posso calcolare lo sforzo di compressione N

N= (q trave x q solaio) x n piani= 1201 KN

parte 3 e 4 Le ultime due parti del foglio excel permettono di ricavare l’area minima che deve avere la sezione in modo tale che il materiale non arrivi a rottura (Amin) e poi di ricavare il momento di inerzia minimo di progetto (Imin)

step 5 inserisco la tensione di snervamento (f_ck) 40 MPa 

(f_cd) 22,7 MPa, l’area minima Amin =530 cm2 e min = 23 cm

step 6 Sapendo che Il modulo di elasticità E = 210000 MPa, β =1 e l’altezza del pilastro è di 2,75 m, posso procedere con:

1. il calcolo del valore massimo di snellezza λ_{max =} 95,62
2. il valore minimo del raggio di inerzia ρ_min = 2,88 cm
3. calcolo la grandezza della base b min = 2 x rad3 x ρ_min = 9,96 cm, che ingegnerizzo scegliendo una b = 30 cm. 
4. calcola l’altezza minima h_min =   A_min / b = 17,67 cm —>  h= 40 cm

step 7 devo verificare che A_design > A_min   1200 > 530  AREA VERIFICATA

step 8 sapendo che:

- I_design= h x b^3 /12 = 90000 cm4

• I_max = b x h^3 /12 = 160000 cm4
• W_max =(modulo di resistenza a flessione) = b x h^2 / 6= 8000 cm3
• carico distribuito sulla trave q =(1,3 x qs + 1,5 x qp + 1,5 x qa) x L2 = 65,72 KN/m
• momento nell’estremo della trave M= q x L1^2 /12 = 87,63 KNm

step 9 calcolo la tensione massima

σ_max = 20,97 MPa

step 10 σ_max < f_cd     20,97 < 22,7  TENSIONE VERIFICATA

La terza esercitazione prevede il dimensionamento di una trave a sbalzo, e come fatto nel dimensionamento della trave maggiormente sollecitata nella prima esercitazione, useremo tre materiali differenti: legno, acciaio e calcestruzzo armato. 

PER I PACCHETTI SOLAIO E I CARICHI APPLICATI faccio riferimento alla prima esercitazione postata.

http://design.rootiers.it/strutture/node/1685

La prima parte dell’analisi per ciascuna trave nelle tre tecnologie risulta uguale alla prima esercitazione: si ragiona alla SLU(stato limite ultimo), poiché si otteneva una h min per mezzo del qu, considerando lo stato ultimo della struttura (collasso). La seconda parte invece riguarda l’analisi allo SLE (stato limite di esercizio), in questa verifica la struttura non viene compromessa ma abbiamo fenomeni di instabilità e vibrazioni. Partendo dal qe ottengo un vmax.

All’interno del telaio scelto (usato per tutte e tre le analisi), si individua la trave a sbalzo maggiormente sollecitata e si evidenzia la sua area di influenza.  La trave presa in esame è la trave lungo l’asse B, che individua un’area di interasse 3,5 m e una luce di 3 m. Nel caso della trave a sbalzo (mensola) il momento massimo è differente rispetto a quello di una trave doppiamente appoggiata. Mmax= ql2/2

LEGNO

totale qs (0.15 + 0.24) KN/mq = 0.39 KN/mq

totale qp (1 + 0.5 + 0.72 + 0.45 + 0.54 + 0.16) KN/mq = 3.37 KN/mq

ambiente ad uso residenziale 2 KN/mq

qu= (1,3 x 0.39 + 1,5 x 3.37 + 1,5 x 2) x 3 = 29,97 KN/m

Il momento max risulta: Mmax= ql2/2= 134,85 KNm

Impostando i dati relativi al materiale e impostando una base b= 30 cm ottengo una hmin= 53,00 cm. Ingegnerizzo la sezione con h= 55 cm. 

Una volta impostata la sezione posso iniziare la verifica allo stato limite di esercizio

qe= (qs + qp + 0,5 x qa) x interasse

qe= (0,39 + 3,37 + 0,5 x 2) x 3,5= 17 KN/m

Imposto il modulo elastico E = 8000 MPa e ottengo una Ix= (b x h3)/12= 415938 cm4

Dopo aver calcolato il Vmax= 0,51 cm, posso passare alla verifica Ix/vmax >250

SEZIONE VERIFICATA

Aggiungendo il peso proprio della trave:

p= (0,3 x 0,55 x 1) x 5 = 0,825 KN/mq

qu= 29,97 + 1,3 x 0,825= 31,04 KN/m

La sezione ingegnerizzata risulta comunque verificata.

ACCIAIO 

totale qs (0.224 + 0.1 + 0.96) KN/mq = 1.28 KN/mq

totale qp (1 + 0.5 + 0.54 + 0.36 + 0.16 + 0.163) KN/mq = 2.69 KN/mq

ambiente ad uso residenziale 2 KN/mq

q= (1,3 x 1.28 + 1,5 x 2.69 + 1,5 x 2) x 3,5 = 30,45 KN/m

Il momento max risulta: Mmax= ql2/2= 137,01 KNm

Impostando i dati relativi al materiale fyk =235 MPA ottengo un Wx,min= 612,17 cm3.

Per questo motivo ho selezionato come profilo un IPE 300 con un Wx pari a 628,36 cm3.

Posso iniziare ora la verifica allo stato limite di esercizio

qe= (qs + qp + 0,5 x qa) x interasse + peso

qe= (1,28 + 2,69 + 0,5 x 2) x 3,5 + 0,42= 17,82 KN/m

Imposto il modulo elastico E = 8000 MPa e ottengo una Ix= (b x h3)/12= 210000 cm4

Dopo aver calcolato il Vmax= 1,028 cm, posso passare alla verifica Ix/vmax >250

291,9>250

SEZIONE VERIFICATA

CALCESTRUZZO ARMATO

totale qs (0.672 + 0.6 + 0.96) KN/mq = 2.23 KN/mq

totale qp (1 + 0.5 + 0.54 + 0.36 + 0.18 + 0.12) KN/mq = 2.37 KN/mq

ambiente ad uso residenziale 2 KN/mq

q= (1,3 x 2.23 + 1,5 x 2.37 + 1,5 x 2) x 3,5 = 33,09 KN/m

Il momento max risulta: Mmax= ql2/2= 148,9 KNm

Imposto i dati relativi al materiale scelto (fyk e fck) e ottengo per una base di 30 cm, un’altezza minima di 46,28 cm che ingegnerizzo con una h=50 cm

Anche aggiungendo ai carichi il peso proprio della trave

q trave (0.006261) mc/mq x 78.5 KN/ mc = 0.49 KN/mq

q= (1,3 x 2.23 + 1,5 x 2.37 + 1,5 x 2) x 43,5 + 1,3 x 0.49 =33,58 KN/m

La sezione scelta risulta comunque verificata.

Posso iniziare ora la verifica allo stato limite di esercizio: qe= 23,35 KN/m

Imposto il modulo elastico E = 21000 MPa e ottengo una  Ix= (b x h3)/12= 312500 cm4

Dopo aver calcolato il Vmax= 0,36 cm, posso passare alla verifica Ix/vmax >250

832,74>250

SEZIONE VERIFICATA

La seconda esercitazione si basa sull’analisi e sul dimensionamento di una struttura reticolare tridimensionale in acciaio costituita da elementi strutturali base (aste), che vengono collegate tra loro da nodi. Questi nodi vengono considerati come cerniere interne che consentono alle aste tutte le rotazioni possibili nello spazio. 

Le aste reticolari sono dunque sollecitate solo a SFORZO NORMALE (sia trazione che compressione), mentre tutte le altre sollecitazioni (taglio, flessione e torsione) sono assenti. L’utilizzo di queste particolari strutture permette di realizzare coperture con grandi luci, senza pilastri intermedi.

Attraverso il software SAP 2000 ho potuto modellare la struttura reticolare, partendo dal costruire un singolo modulo tridimensionale (piramide) , che verrà poi ripetuto per l’intera maglia strutturale. 

step 1 Apro un nuovo file (New model), cambio l’unità di misura (KN, m, C) e scelgo come spazio di lavoro (Grid Only).

step 2 Imposto la maglia strutturale composta da cubi di lato L = 2,00 m, e dispongo 4 cubi lungo l’asse x e ripeto questi cubi per 3 volte lungo l’asse y.  Uso quindi una griglia: x=5 y=4 z=2

step 3 Scelgo come modulo base quello piramidale ed inizio a disegnare all’interno di ogni cubo una piramide con il vertice rivolto verso il basso. (frame draw) In seguito collego i vertici con delle aste sia ortogonali agli assi sia diagonali in modo da contraventare l’intera struttura. 

step 4 Cliccando su edit -> edit points -> merge duplicate posso controllare se ci sono delle aste doppie, e procedere dunque all’analisi.

step 5 Poichè la struttura nasce dalla ripetizione di un unico modulo, è opportuno correggere la tolleranza di 0,1 edit -> edit points -> merge joints

step 6 Selezioni i quattro vertici agli estremi situati sul piano z=0 e aggiungo dei vincoli cerniere 

assign -> joint -> Restraints

step 7 Poichè per natura, la struttura reticolare lavoro solo a sforzo normale, bisogna svincolare i nodi al momento. assign -> frame ->Release/ partial fixity

step 8 Definisco ora il materiale che compone la struttura e il profilo che deve avere

Frame -> frame sections -> add new property -> pipe

step 9 Facendo attenzione a selezionare solamente i nodi superiori, imposto il carico distribuito sull’intera struttura, aggiungendo una forza F = -150 KN

Assigne -> Joint loads -> Forces

step 10 A questo punto posso iniziare l’analisi lineare statica cliccando su Run analysis e selezionando solamente la forza F = -150 KN.

step 11 Controllo inoltre che sulla struttura siano presenti solo sforzi normali

Frame -> Axiel force

step 12 Esporto tutti i dati relativi agli sforzi di compressione e di trazione su un foglio Excel per iniziare il dimensionamento delle singole aste.

step 13 una volta esportati tutti gli sforzi normali, elimino tutti i duplicati presenti e ordino i risultati ottenuti dal più piccolo al più grande in modo da aver distinti gli sforzi di trazione (+) da quelli di compressione (-)

step 14 vista la struttura piramidale del singolo modulo, ho aste di differenti dimensioni:

1) aste ortogonali al piano x-y: 2,00 m

2) aste inclinate: 2,45 m

3) aste diagonali: 2,83 m

step 15 compilo il foglio riguardante gli sforzi di trazione

1. inserisco tutti gli sforzi di trazione
2. Aggiungo le caratteristiche dell’acciaio scelto con tensione di snervamento  fyk =235 MPa
3. Aggiungo il coefficiente γ_s 1,05 
4. calcolo fyd di progetto = 235 x 1,05= 223,81 Mpa
5. Ottengo dunque moltiplicando la tensione di progetto per lo sforzo l’area minima della sezione espressa in cm2.
6. Guardando il profilario procedo con il dimensionamento delle aste scegliendo i vari profili, che devono avere ovviamente un’area maggiore dell’area minima ottenuta dai calcoli.

step 16 sforzi di compressione

Per la compressione valgono gli stesi procedimenti fatti precedentemente, con l’aggiunta del fenomeno di instabilità.

1. aggiungo i valori di E= 210000 Mpa , beta= 1 e la lunghezza delle singole aste 
2. Ottengo tre dati molto importanti:

• Lambda= pigreco x rad(E/fcd)
• Rho minimo= (beta x l x 100)/lambda
• I min= Amin x Rho min

3) posso procedere ora al dimensionamento delle aste facendo attenzione che il lambda finale risulti comunque < 200

La prima esercitazione consiste nel dimensionare a flessione la trave più sollecitata appartenente ad un telaio di nostra scelta (uno in legno, uno in acciaio ed uno in cemento armato).  Il telaio scelto è composto da 4 campate: 2 (4 m di interasse x 4 m di luce) e 2 (4 m di interasse x 6 di luce). L'esercitazione si compone di tre analisi indipendenti, una per ogni sistema tecnologico.

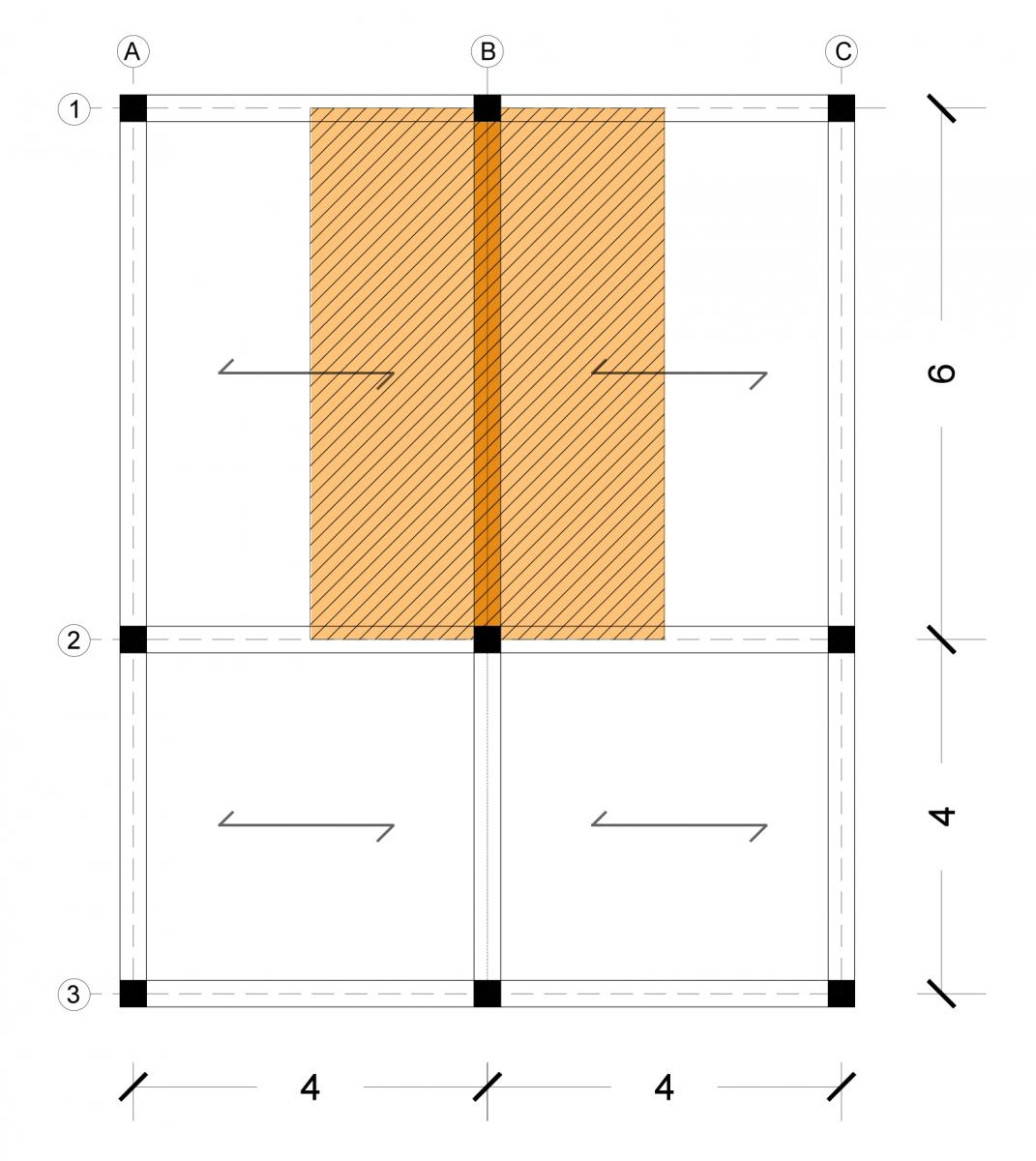                                                                             Dall'analisi del solaio, si può notare come la trave soggetta a maggior carico e di conseguenza al maggior momento flettente è quella messa in evidenza, infatti la sua area di influenza è pari a 24 mq (4 m interasse x 6 m luce).

FASI OPERATIVE:

1_ Analisi dei carichi distribuiti (KN/mq) 

    (peso specifico del materiale x volume) / 1 mq

I carichi distribuiti sono divisi in:

qs carichi strutturali: comprendono tutti gli elementi con funzione strutturale (escludendo il peso proprio della trave)

qp carichi permanenti: comprendono tutti gli elementi presenti sul solaio ma che non hanno una funzione strutturale

qa carichi accidentali: nominati dalla normativa tecnica e dipendono dalla destinazione d’uso (commerciale, residenziale ecc). 

2_ I carichi qs, qp e qa vengono sommati e moltiplicati per l’interasse per ottenere q (KN/m):

q= (1,3 x qs + 1,5 x qp + 1,5 x qa) x interasse

I singoli carichi vengono moltiplicati per dei coefficienti di sicurezza 1,3 e 1,5.

PRIMA TECNOLOGIA: il legno

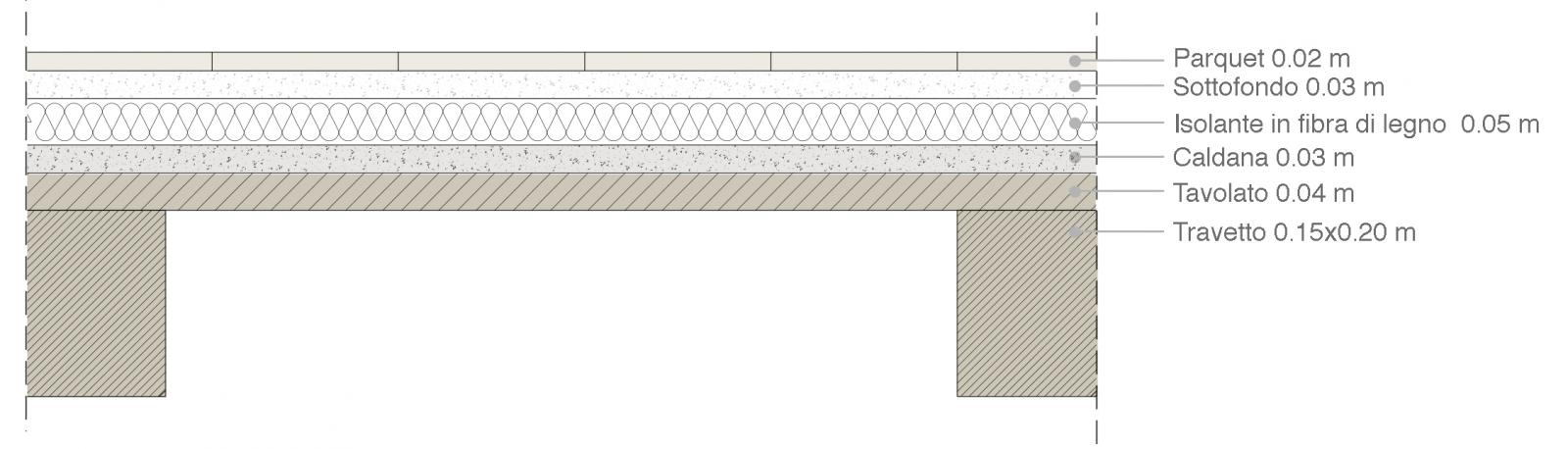
Pesi specifici dei materiali che compongono il solaio:

Parquet: 8 KN/mc

Sottofondo: 18 KN/mc

Isolante in fibra di legno: 9 KN/mc

Caldana: 24 KN/mc

Tavolato: 6 KN/mc

Travetti: 5 KN/mc

1_ CARICHI STRUTTURALI qs

travetti (0.2 x 0.15 x 1) mc/mq x 5 KN/mc = 0.15 KN/mq

tavolato (0.04 x 1 x 1) mc/mq x 6 KN/mc = 0.24 KN/mq

totale qs (0.15 + 0.24) KN/mq = 0.39 KN/mq

2_ CARICHI PORTATI qp

tramezzi 1 KN/mq

impianti 0.5 KN/mq 

caldana (0.03 x 1 x 1) mc/mq x 24 KN/mc = 0.72 KN/mq

isolante (0.05 x 1 x 1) mc/mq x 9 KN/mc = 0.45 KN/mq

sottofondo (0.03 x 1 x 1) mc/mq x 18 KN/mc = 0.54 KN/mq

pavimento (0.02 x 1 x 1) mc/mq x 8 KN/mc = 0.16 KN/mq

totale qp (1 + 0.5 + 0.72 + 0.45 + 0.54 + 0.16) KN/mq = 3.37 KN/mq

3_ CARICHI ACCIDENTALI qa

ambiente ad uso residenziale 2 KN/mq

Questi valori ora attraverso il foglio excel vengono sommati tra loro per ottenere q (KN/mq).

q= (1,3 x qs + 1,5 x qp + 1,5 x qa) x interasse

q= (1,3 x 0.39 + 1,5 x 3.37 + 1,5 x 2) x 4 = 34.25 KN/m

Conoscendo il carico gravante sulla trave e la luce di questa si può ricavare il momento della trave appoggiata (M = q x l2/8).  M= 34.25 x 36/ 8= 154.12 KNm.

Per la realizzazione di questo solaio è stato scelto un legno lamellare GL24h con una resistenza caratteristica  f m,k = 24 MPa. si può calcolare quindi la resistenza di progetto f_d, e impostando la base della trave si ricaverà l’altezza. Una volta trovata h è opportuno ingegnerizzare l’altezza trovata in modo da ottenere una trave con una sezione standardizzata. 

L’altezza attraverso la formula di Navier è pari a 48,25 cm, per questo motivo ho scelto una trave con sezione 30 x 50 cm.

I calcoli precedenti però non tenevano in considerazione il peso proprio della trave, bisogna quindi ripetere i calcoli aggiungendo ai carichi strutturali qs il peso p, e verificare se la trave dimensionata 30 x 50 cm risulta adeguata. 

p = (0.3 x 0.5 x 1) mc/mq x 5 KN/ mc = 0.75 KN/mq

q= (1,3 x 0.39 + 1,5 x 3.37 + 1,5 x 2) x 4 + 1,3 x 0.75 = 35,23 KN/m

Una volta aggiunto il peso proprio della trave all’interno del foglio excel l’altezza ottenuta è pari a 48.93 cm.  Dal dimensionamento si nota che il calcolo precedentemente svolto era corretto: aggiungendo il peso della trave la sezione scelta 30 x 50 cm è in grado di sorreggere i carichi qs, qp e qa che gravano sul solaio. (sezione verificata)

SECONDA TECNOLOGIA: l’acciaio

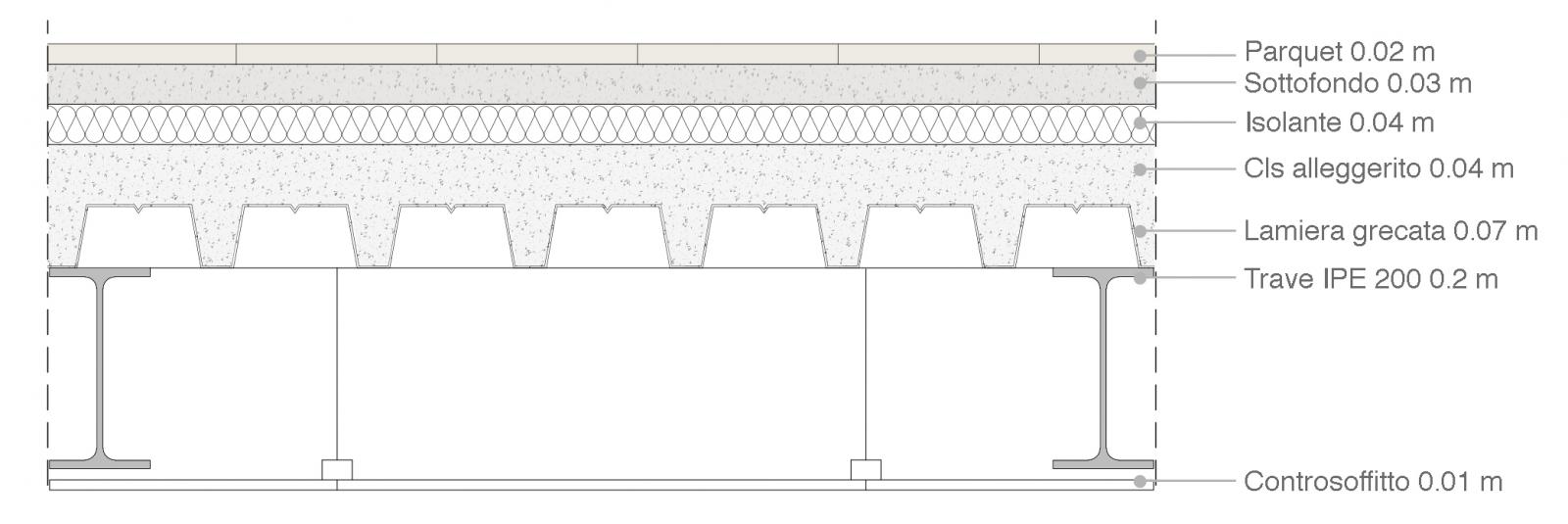
Pesi specifici dei materiali che compongono il solaio:

Parquet: 8 KN/mc

Massetto: 18 KN/mc

Isolante: 9 KN/mc

Getto in cls: 24 KN/mc

Lamiera grecata: 0.10 KN/mq

Trave IPE 200: 78.5 KN/mc

Controsoffitto: 13 KN/mc

1_ CARICHI STRUTTURALI qs

travetti (0.00285 x 1) mc/mq x 78.5 KN/mc = 0.224 KN/mq

lamiera 0.10 KN/mq

getto cls (0.04 x 1 x 1) mc/mq x 24 KN/mc = 0.96 KN/mq

totale qs (0.224 + 0.1 + 0.96) KN/mq = 1.28 KN/mq

2_ CARICHI PORTATI qp

tramezzi 1 KN/mq

impianti 0.5 KN/mq 

massetto (0.03 x 1 x 1) mc/mq x 18 KN/mc = 0.54 KN/mq

isolante (0.04 x 1 x 1) mc/mq x 9 KN/mc = 0.36 KN/mq

pavimento (0.02 x 1 x 1) mc/mq x 8 KN/mc = 0.16 KN/mq

controsoffitto (0.01 x 1 x 1) mc/mq x 13 KN/mc = 0.13 KN/mq

totale qp (1 + 0.5 + 0.54 + 0.36 + 0.16 + 0.163) KN/mq = 2.69 KN/mq

3_ CARICHI ACCIDENTALI qa

ambiente ad uso residenziale 2 KN/mq

Questi valori ora, attraverso il foglio excel, vengono sommati tra loro per ottenere q (KN/mq).

q= (1,3 x qs + 1,5 x qp + 1,5 x qa) x interasse

q= (1,3 x 1.28 + 1,5 x 2.69 + 1,5 x 2) x 4 = 34.80 KN/m

Dalla tabella excel si ottiene un modulo di resistenza Wx pari a 597.86 cm3. Per questo motivo ho selezionato come profilo un IPE 330 con un Wx pari a 713.1 cm3.

Anche per la trave in acciaio i calcoli precedenti non tenevano in considerazione il peso proprio della trave, bisogna quindi ripetere i calcoli aggiungendo a q il peso p, e verificare se il profilo IPE 330 risulta adeguato.

p = (0.006261) mc/mq x 78.5 KN/ mc = 0.49 KN/mq

q = (1,3 x 1.28 + 1,5 x 2.69 + 1,5 x 2) x 4 + 1,3 x 0.49 = 35,44 KN/m

Nonostante nel primo predimensionamento non era stato considerato il peso proprio della trave, il profilo IPE 330 scelto risulta comunque idoneo. (Profilo IPE 330 verificato)

TERZA TECNOLOGIA: il cemento armato

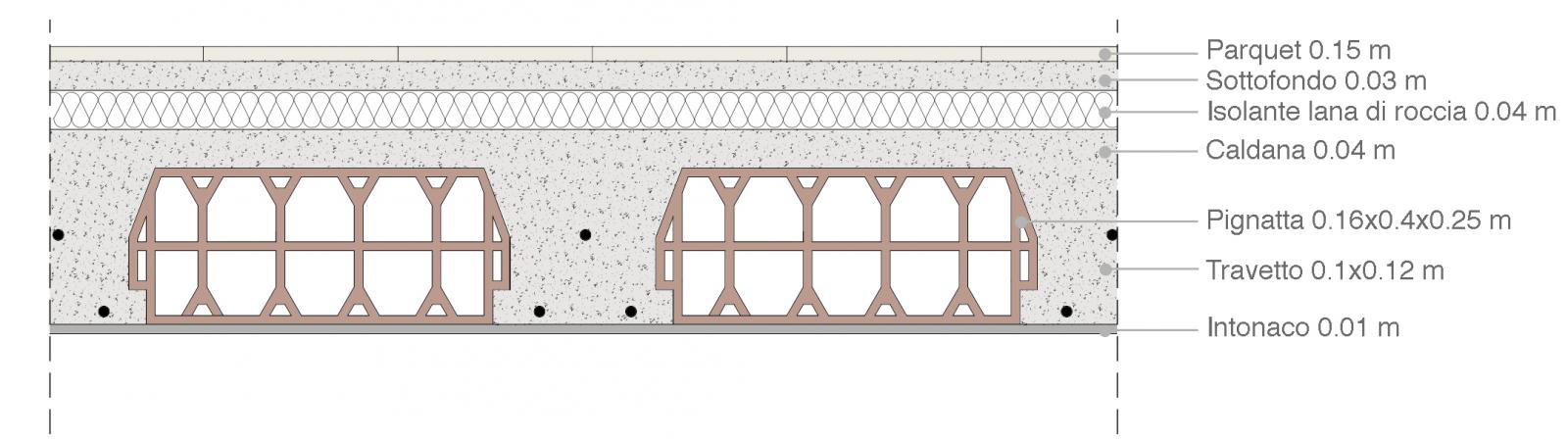
Pesi specifici dei materiali che compongono il solaio:

Parquet: 8 KN/mc

Sottofondo: 18 KN/mc

Isolante in lana di roccia: 0.9 KN/mc

Getto in cls: 24 KN/mc

Travetto: 25 KN/mq

Pignatta: 8.7 kg

Intonaco: 18 KN/mc

1_ CARICHI STRUTTURALI qs

travetti (0.1 x 0.12 x 1) mc/mq x 25 KN/mc x 2 = 0.6 KN/mq

pignatte (8 x 8.7 kg/mq) = 67.2 kg/mq = 0.672 KN/mq

soletta collaborante (0.04 x 1 x 1) mc/mq x 24 KN/mc = 0.96 KN/mq

totale qs (0.672 + 0.6 + 0.96) KN/mq = 2.23 KN/mq

2_ CARICHI PORTATI qp

tramezzi 1 KN/mq

impianti 0.5 KN/mq 

massetto (0.03 x 1 x 1) mc/mq x 18 KN/mc = 0.54 KN/mq

isolante (0.04 x 1 x 1) mc/mq x 0.9 KN/mc = 0.036 KN/mq

pavimento (0.015 x 1 x 1) mc/mq x 8 KN/mc = 0.12 KN/mq

intonaco (0.01 x 1 x 1) mc/mq x 18 KN/mc = 0.18 KN/mq

totale qp (1 + 0.5 + 0.54 + 0.36 + 0.18 + 0.12) KN/mq = 2.37 KN/mq

3_ CARICHI ACCIDENTALI qa

categoria b2 - uffici aperti al pubblico 3 KN/mq

Questi valori ora, attraverso il foglio excel, vengono sommati tra loro per ottenere q (KN/mq).

q= (1,3 x qs + 1,5 x qp + 1,5 x qa) x interasse

q= (1,3 x 2.23 + 1,5 x 2.37 + 1,5 x 3) x 4 = 43.82 KN/mq

Per la realizzazione di questo solaio è stato scelto un acciaio con una resistenza caratteristica      f _y,k = 450 MPa e un calcestruzzo con resistenza a compressione R_ck pari a 50 MPa e impostyamdo una base di 30 cm avremo una altezza minima di 37,84 cm. Ingegnerizzo la sezione con b= 30cm e h= 40 cm.

Anche per la trave in cls i calcoli precedenti non tenevano in considerazione il peso proprio della trave, bisogna quindi ripetere i calcoli aggiungendo a q il peso p, e verificare se sezione risulta adeguato.

q trave (0.006261) mc/mq x 78.5 KN/ mc = 0.49 KN/mq

q= (1,3 x 2.23 + 1,5 x 2.37 + 1,5 x 2) x 4 + 1,3 x 0.49 = 44,46 KN/m

Nonostante nel primo predimensionamento non era stato considerato il peso proprio della trave, il profilo IPE 330 scelto risulta comunque idoneo.  (sezione 30 x 40 cm verificata)