ESERCITAZIONE 3_ Dimensionamento trave a sbalzo

La terza esercitazione prevede il dimensionamento di una trave a sbalzo, e come fatto nel dimensionamento della trave maggiormente sollecitata nella prima esercitazione, useremo tre materiali differenti: legno, acciaio e calcestruzzo armato. 

PER I PACCHETTI SOLAIO E I CARICHI APPLICATI faccio riferimento alla prima esercitazione postata.

http://design.rootiers.it/strutture/node/1685

La prima parte dell’analisi per ciascuna trave nelle tre tecnologie risulta uguale alla prima esercitazione: si ragiona alla SLU(stato limite ultimo), poiché si otteneva una h min per mezzo del qu, considerando lo stato ultimo della struttura (collasso). La seconda parte invece riguarda l’analisi allo SLE (stato limite di esercizio), in questa verifica la struttura non viene compromessa ma abbiamo fenomeni di instabilità e vibrazioni. Partendo dal qe ottengo un vmax.

All’interno del telaio scelto (usato per tutte e tre le analisi), si individua la trave a sbalzo maggiormente sollecitata e si evidenzia la sua area di influenza.  La trave presa in esame è la trave lungo l’asse B, che individua un’area di interasse 3,5 m e una luce di 3 m. Nel caso della trave a sbalzo (mensola) il momento massimo è differente rispetto a quello di una trave doppiamente appoggiata. Mmax= ql2/2

LEGNO

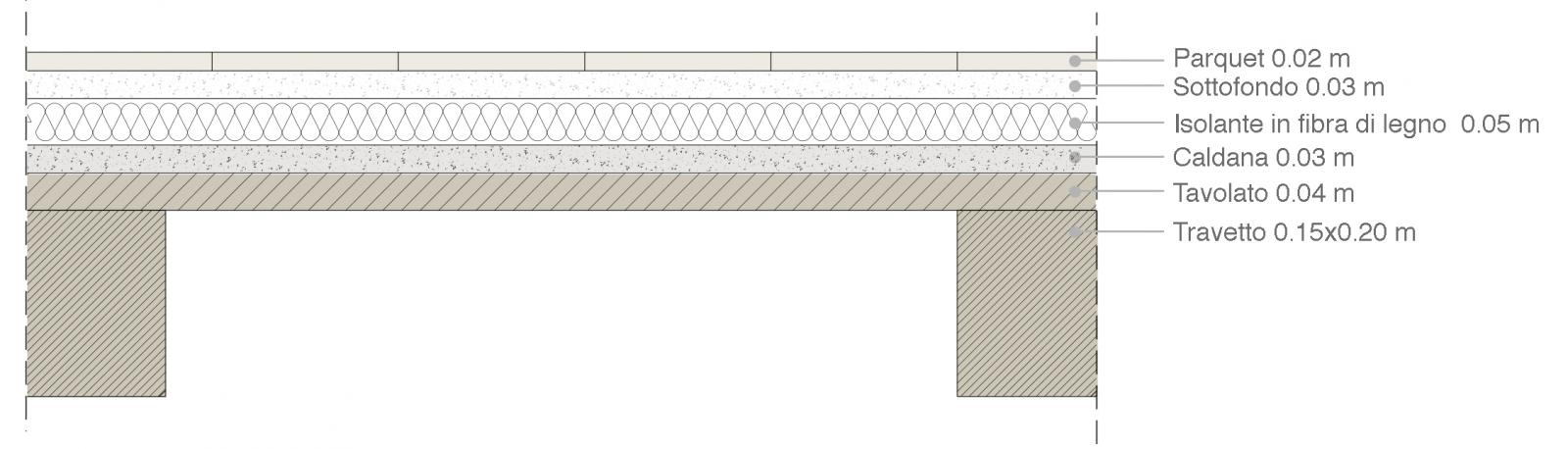
totale qs (0.15 + 0.24) KN/mq = 0.39 KN/mq

totale qp (1 + 0.5 + 0.72 + 0.45 + 0.54 + 0.16) KN/mq = 3.37 KN/mq

ambiente ad uso residenziale 2 KN/mq

qu= (1,3 x 0.39 + 1,5 x 3.37 + 1,5 x 2) x 3 = 29,97 KN/m

Il momento max risulta: Mmax= ql2/2= 134,85 KNm

Impostando i dati relativi al materiale e impostando una base b= 30 cm ottengo una hmin= 53,00 cm. Ingegnerizzo la sezione con h= 55 cm. 

Una volta impostata la sezione posso iniziare la verifica allo stato limite di esercizio

qe= (qs + qp + 0,5 x qa) x interasse

qe= (0,39 + 3,37 + 0,5 x 2) x 3,5= 17 KN/m

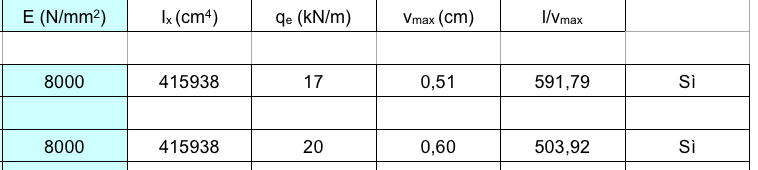
Imposto il modulo elastico E = 8000 MPa e ottengo una Ix= (b x h3)/12= 415938 cm4

Dopo aver calcolato il Vmax= 0,51 cm, posso passare alla verifica Ix/vmax >250

SEZIONE VERIFICATA

Aggiungendo il peso proprio della trave:

p= (0,3 x 0,55 x 1) x 5 = 0,825 KN/mq

qu= 29,97 + 1,3 x 0,825= 31,04 KN/m

La sezione ingegnerizzata risulta comunque verificata.

ACCIAIO 

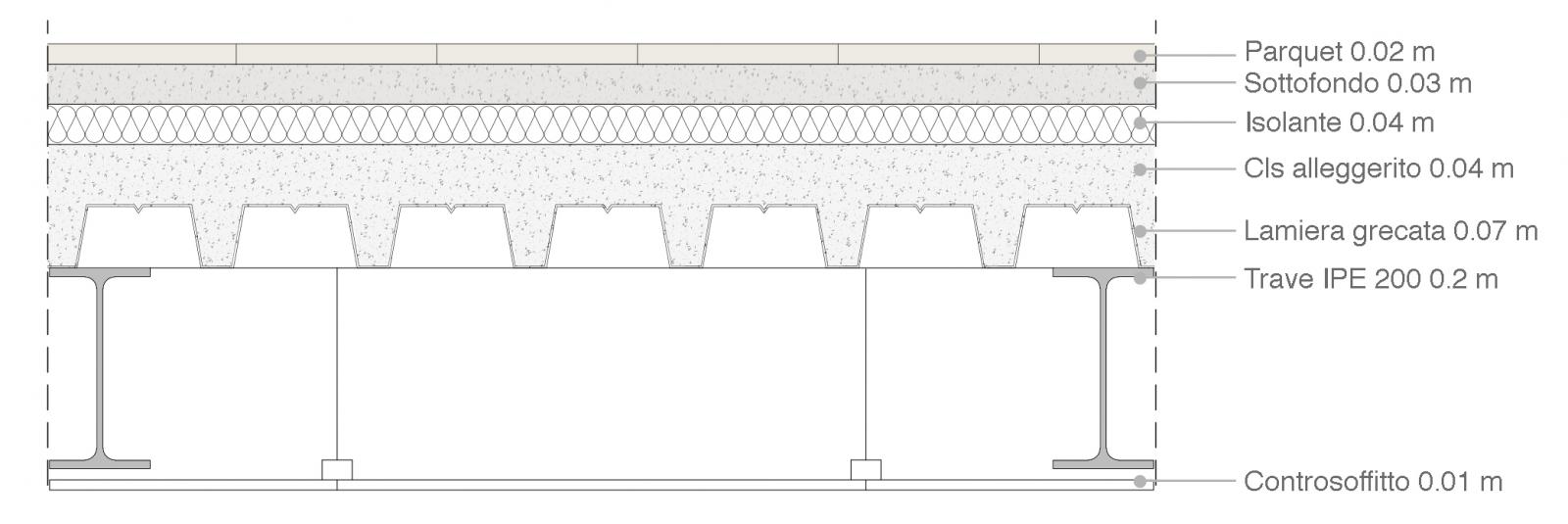
totale qs (0.224 + 0.1 + 0.96) KN/mq = 1.28 KN/mq

totale qp (1 + 0.5 + 0.54 + 0.36 + 0.16 + 0.163) KN/mq = 2.69 KN/mq

ambiente ad uso residenziale 2 KN/mq

q= (1,3 x 1.28 + 1,5 x 2.69 + 1,5 x 2) x 3,5 = 30,45 KN/m

Il momento max risulta: Mmax= ql2/2= 137,01 KNm

Impostando i dati relativi al materiale fyk =235 MPA ottengo un Wx,min= 612,17 cm3.

Per questo motivo ho selezionato come profilo un IPE 300 con un Wx pari a 628,36 cm3.

Posso iniziare ora la verifica allo stato limite di esercizio

qe= (qs + qp + 0,5 x qa) x interasse + peso

qe= (1,28 + 2,69 + 0,5 x 2) x 3,5 + 0,42= 17,82 KN/m

Imposto il modulo elastico E = 8000 MPa e ottengo una Ix= (b x h3)/12= 210000 cm4

Dopo aver calcolato il Vmax= 1,028 cm, posso passare alla verifica Ix/vmax >250

291,9>250

SEZIONE VERIFICATA

CALCESTRUZZO ARMATO

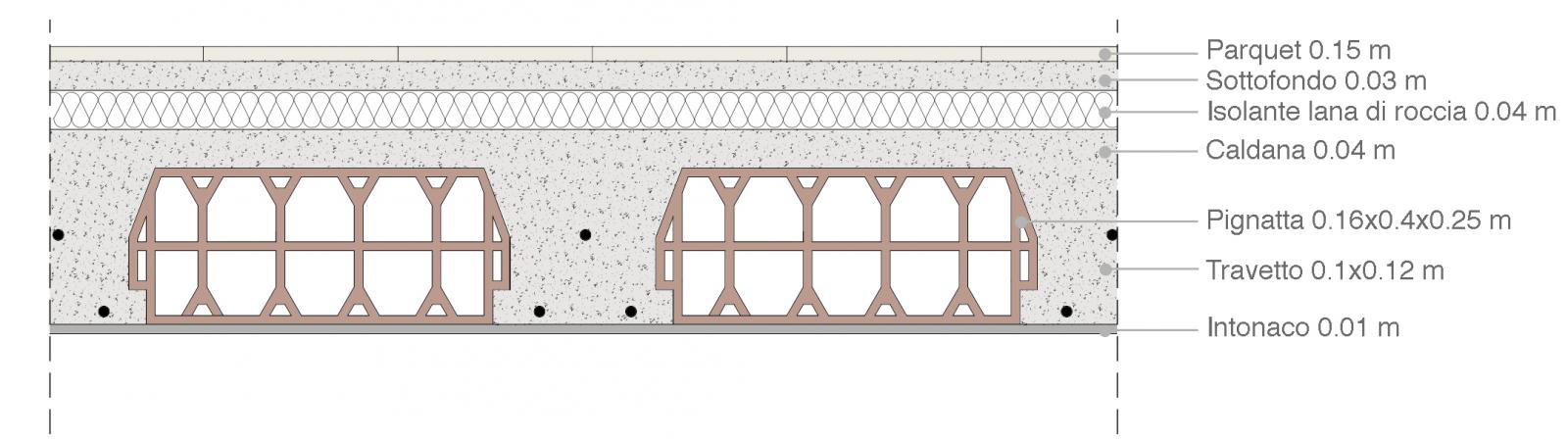
totale qs (0.672 + 0.6 + 0.96) KN/mq = 2.23 KN/mq

totale qp (1 + 0.5 + 0.54 + 0.36 + 0.18 + 0.12) KN/mq = 2.37 KN/mq

ambiente ad uso residenziale 2 KN/mq

q= (1,3 x 2.23 + 1,5 x 2.37 + 1,5 x 2) x 3,5 = 33,09 KN/m

Il momento max risulta: Mmax= ql2/2= 148,9 KNm

Imposto i dati relativi al materiale scelto (fyk e fck) e ottengo per una base di 30 cm, un’altezza minima di 46,28 cm che ingegnerizzo con una h=50 cm

Anche aggiungendo ai carichi il peso proprio della trave

q trave (0.006261) mc/mq x 78.5 KN/ mc = 0.49 KN/mq

q= (1,3 x 2.23 + 1,5 x 2.37 + 1,5 x 2) x 43,5 + 1,3 x 0.49 =33,58 KN/m

La sezione scelta risulta comunque verificata.

Posso iniziare ora la verifica allo stato limite di esercizio: qe= 23,35 KN/m

Imposto il modulo elastico E = 21000 MPa e ottengo una  Ix= (b x h3)/12= 312500 cm4

Dopo aver calcolato il Vmax= 0,36 cm, posso passare alla verifica Ix/vmax >250

832,74>250

SEZIONE VERIFICATA