Esercitazione2_Dimensionamento di un trave inflessa in legno, acciaio e cemento armato

Con l’esercitazione che segue dimensioniamo, grazie al file Excel fornito, tre travi (rispettivamente in legno, acciaio e calcestruzzo armato) attraverso un metodo di progetto che pone la tensione massima nella trave pari alla tensione di progetto del materiale, definito dalla normativa (viene di conseguenza il fatto che la dimensione di ogni sezione – nel nostro caso l’altezza – ricavata sarà l’altezza minima da prendere in considerazione).

Parto impostando una pianta di carpenteria di un generico edificio (la cui struttura è composta da telai piani, ossia da travi che collaborano con i pilastri). Come da voi suggerito, ai fini dell’esercitazione ritengo il vincolo che il pilastro esercita sulle travi come quella dato da un appoggio semplice.

Individuo quindi la trave principale (ossia la trave posta perpendicolarmente rispetto ai travetti secondari) maggiormente sollecitata (quella con area d’influenza maggiore); nel nostro caso, l’area è pari a 25m², la trave ha una luce di 5m ed un interasse uguale, pari sempre a 5m.

Ipotizzo a questo punto tre solai diversi, rispettivamente in legno, acciaio e calcestruzzo armato.

Devo quindi trovare i diversi valori di carico agenti sul solaio (che esprimerò come densità di carico superficiale in kN/m²) e che mi consentiranno quindi di determinare il carico di progetto sulla trave (questa volta si tratterà tuttavia di una densità di carico lineare, espressa quindi in kN/m).

I carichi agenti sul solaio sono:

i carichi strutturali q_s, ossia i carichi dovuto al peso proprio di tutti gli elementi che svolgono una funzione portante. Nel caso di un solaio in calcestruzzo armato – ad esempio – il peso dei travetti, la soletta corroborante ma anche i mattoni forati;

i carichi permanenti q_p, ossia i carichi dovuto al peso di tutti quegli elementi che gravano sulla struttura portante per il suo intero periodo di vita, pur non svolgendo un ruolo strutturale; Un inciso: nel caso dei tramezzi e degli impianti, non si procede con un calcolo analitico, bensì forfettario che tenga conto di una determinata incidenza a m² (nell0 specifico, 1kN/m² per i tramezzi e 0,5 kN/m² per gli impianti);

 

infine i carichi accidentali q_a, carichi dalla natura fortemente aleatoria quali vento, neve, sisma; ma anche i carichi d’esercizio legati alla funzione che svolgerà l’edificio (per questa esercitazione, sempre su vostro suggerimento, prenderemo in considerazione solamente i carichi d’esercizio regolati dalle NTC2008, ossia le Norme Tecniche per le Costruzioni – D.M. 14 Gennaio 2008);

 

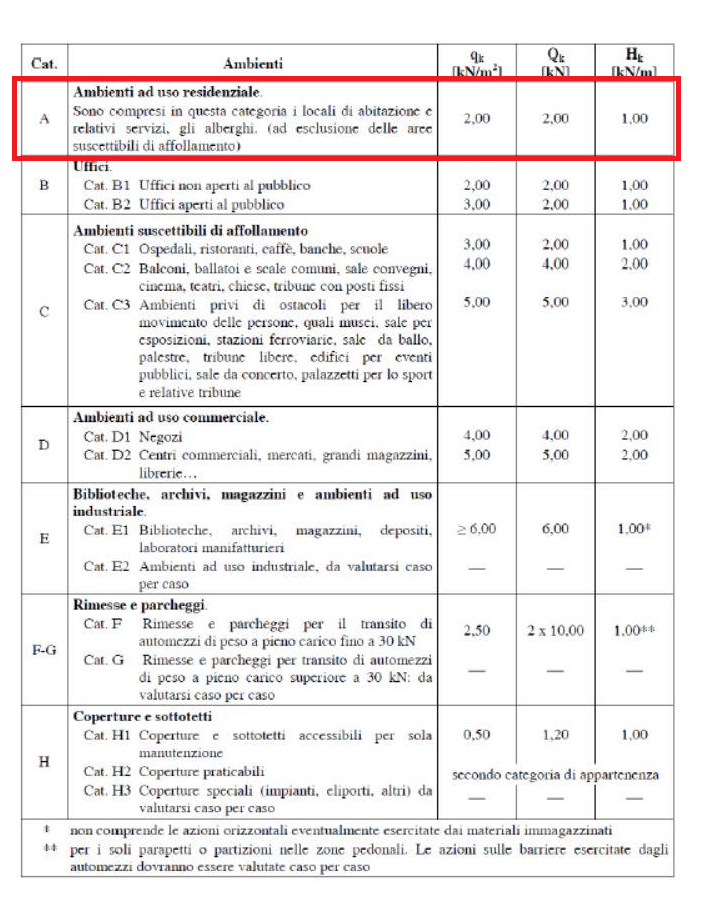
Caliamoci però nello specifico della nostra esercitazione: prendo in analisi 1m² di solaio per ognuno dei tre tipi proposti (scelti in base all’abaco dei modelli UNI10355), distinguo gli elementi strutturali da quelli permanenti e calcolo il peso di ogni materiale contenuto nel m² moltiplicando il suo peso specifico (espresso in KN/m³) per la quantità di volume (espresso in m³/m²).

 

 

 

 

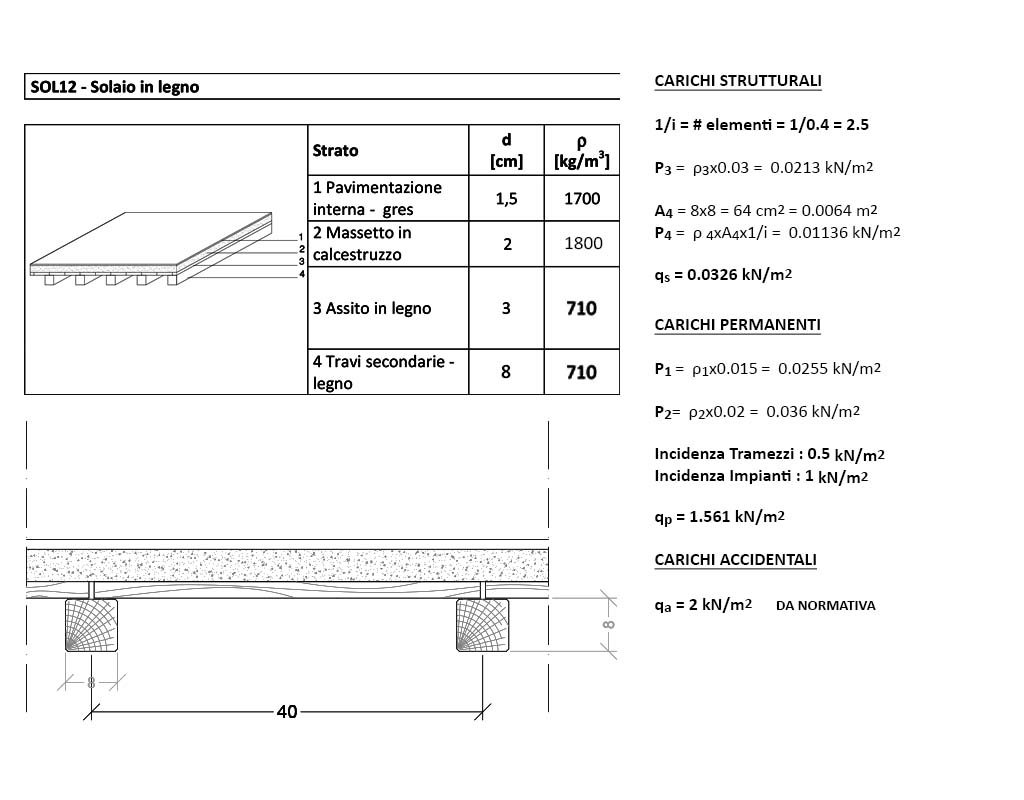
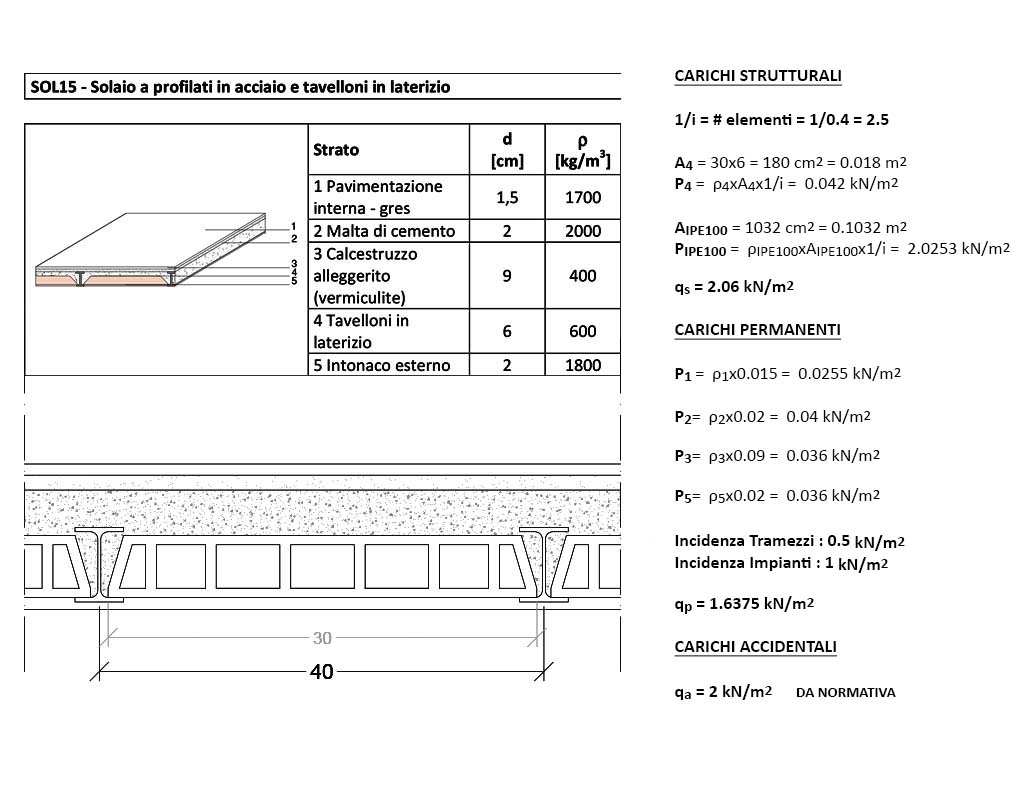
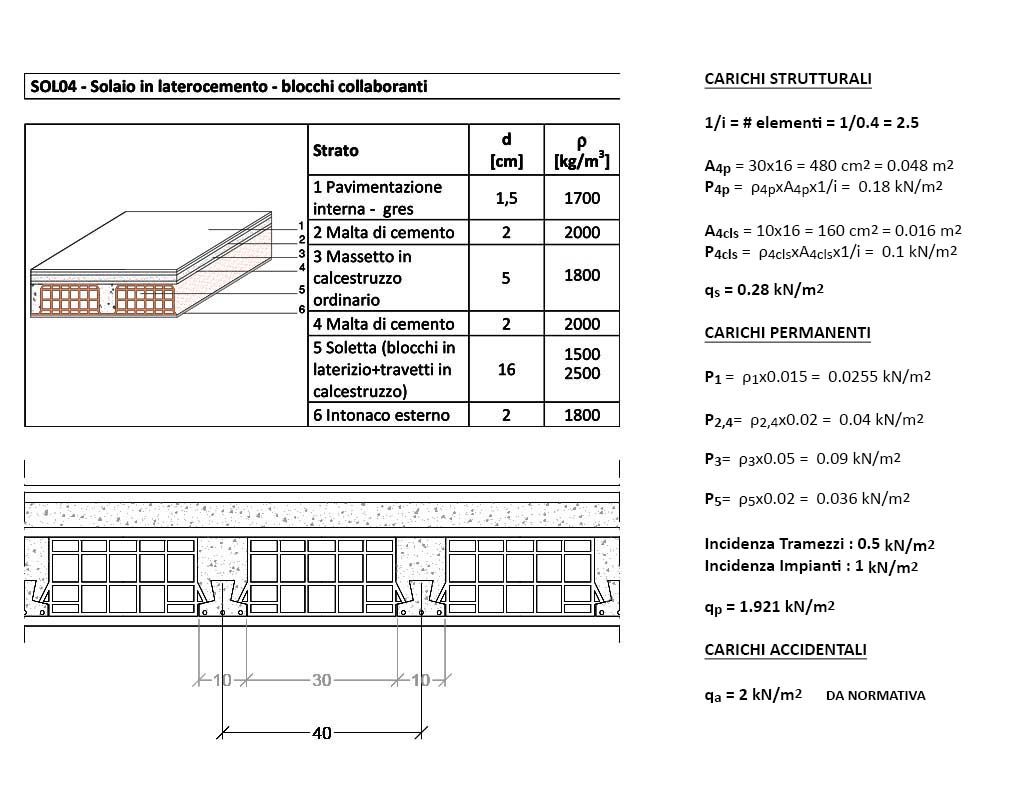
La qu, ossia la combinazione di carico per lo stato limite ultimo (il valore calcolato dal foglio Excel) non è dato dalla semplice somma di q_s, q_p e q_a, bensì dovranno essere tenuti da conto dei coefficienti moltiplicativi dei singoli carichi secondo la combinazione di carico seguente:

q_m²=γ_g1*q_s+ γ_g2*q_p + γ_g3*q_a.

I valori di γ sono riportati nella normativa in funzione dello stato limite ultimo:

 

 

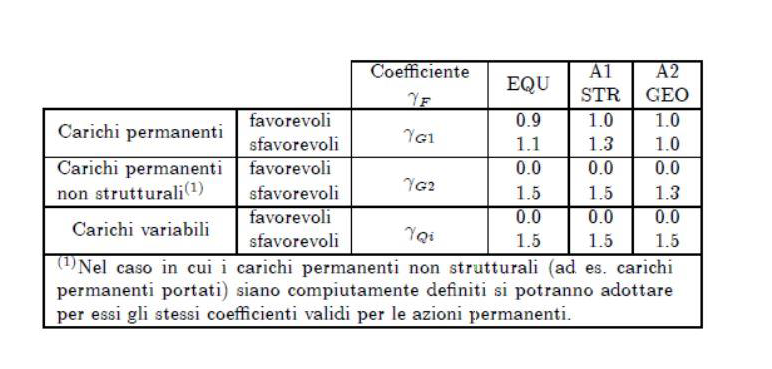
Trovato il valore di carico che si riferisce ad 1m² di solaio (q_m²), per trovare ora il carico agente sulla trave bisognerà innanzitutto trovare la q_solaio agente sull’intero solaio di Area A (con A= area d’influenza = interasse*luce della trave), pari a: q_solaio=q_m²*A

A questo punto, per trovare il carico agente sulla trave basterà dividere il carico appena trovato per l’interasse i. Quindi:

 q_trave=q_solaio/luce= q_m²*i = qu

Determiniamo infine i Momenti Massimi agenti sulla trave. Basterà inserire la luce della trave ed il file Excel lo calcolerà tenendo da conto che ci troviamo dinnanzi l’ipotesi di una trave doppiamente appoggiata

M=(q_u*l²)/8

 

Legno

 

Acciaio

 

Calcestruzzo Armato

Passiamo quindi al dimensionamento della travi, partendo da quella in legno.

Innanzitutto, scegliamo il tipo di legno da utilizzare.

 

 

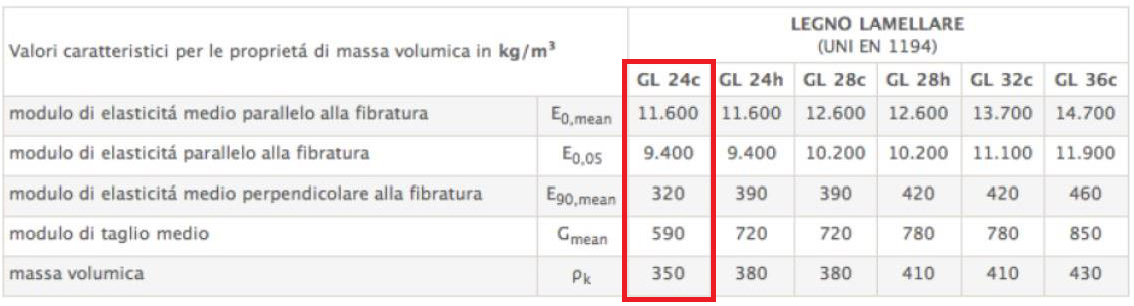
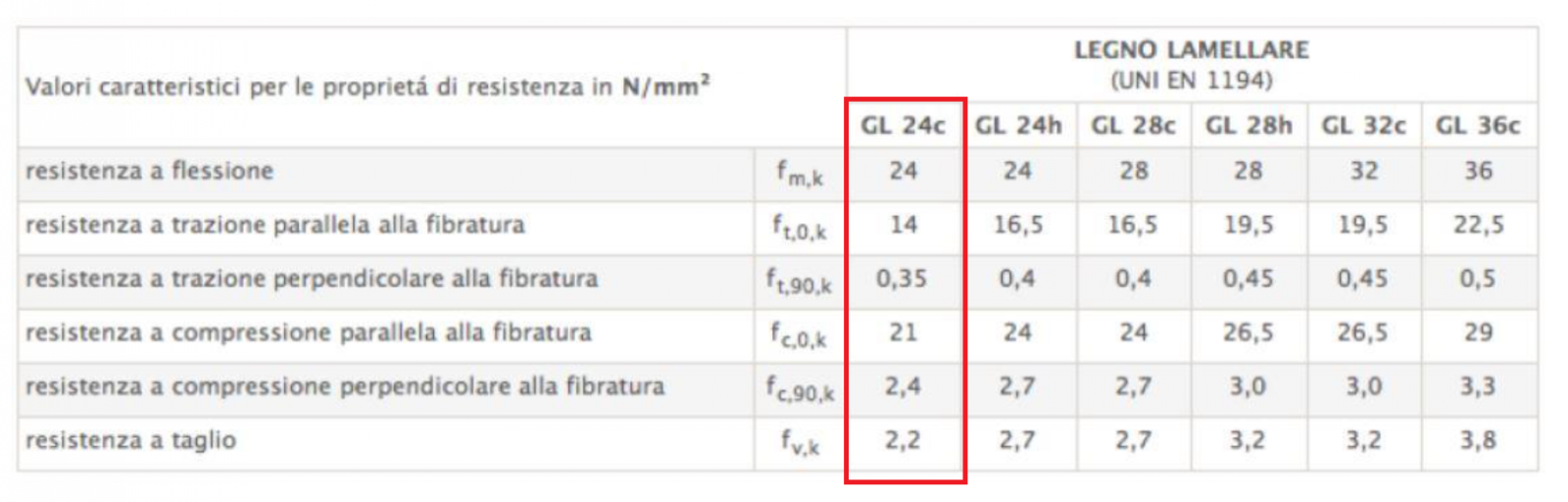
Scegliamo un GL 24c ed inseriamo nella tabella Excel la resistenza caratteristica a flessione f_m,k (dipendente non dall’essenza quanto dalla tecnologia – legno massiccio o lamellare – e dalla classe di resistenza).

La tensione di resistenza f_d sarà a sua volta pari a f_d = (k_mod*f_m,k)/γ_m

K_mod è un coefficiente diminutivo che tiene da conto l’effetto della durata del carico nonché le condizioni di umidità; per definirne il valore è necessario conoscere la durata del carico e la classe di servizio (il tutto è tabellato nelle normative).

Ipotizziamo un carico permanente ed una classe di servizio 2. Dal momento che il nostro è un legno lamellare, avremo un valore k_mod pari a 0,6.

 

 

 

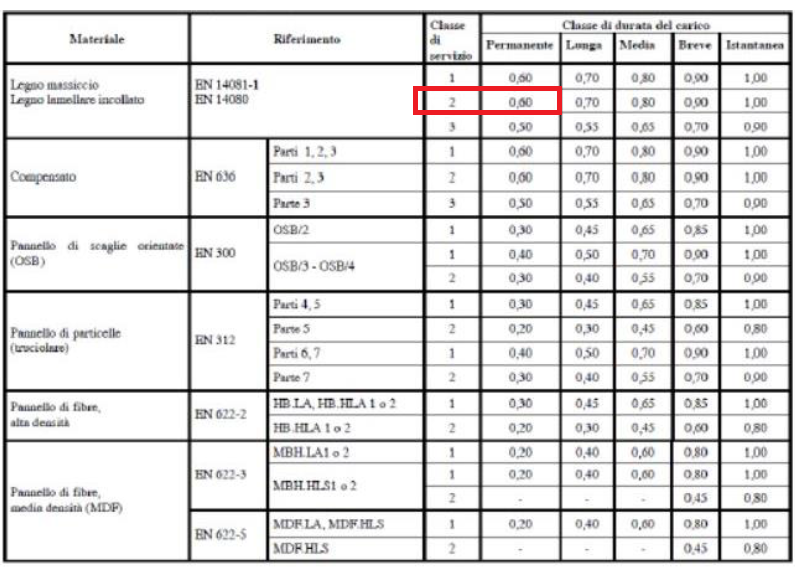
Il coefficiente γ_m è invece un coefficiente parziale di sicurezza relativo al materiale pari – nel nostro caso - ad 1,45 (piuttosto alto se paragonato ai coefficienti di altri paesi).

Inserite quindi le informazioni geometriche, le caratteristiche del materiale e dopo aver determinato le tensioni di progetto, determino la sezione rettangolare scegliendo una base ed ottenendo un’altezza (in estrema sintesi, DATE la base, il Momento Massimo e la tensione di resistenza f_d, ricaviamo l’altezza della nostra sezione). Ipotizzando una base b=30cm

La nostra altezza minima sarà pari a:

h_min= (M_max/b)^0.5 * (6/f_d)^0.5 = 42,46 cm.

Ovviamente questa altezza andrà ingegnerizzata scegliendo un’altezza superiore al valore minimo compatibile con i profili esistenti sul mercato (arrivando – sempre nel nostro caso – ad un’altezza di 50cm).

Ora, riducendo i passaggi all’essenziale, spendiamo due righe su come si è arrivati a calcolare l’altezza minima della nostra trave, partendo dalla formula di Navier per la flessione

σ=(M_x/I_x)*y

Nel momento in cui devo verificare la mia trave, considero

σ_max=(M_max/I_x)*y_max =M_max/W

Con W modulo di resistenza a flessione che dipende dalle caratteristiche geometriche della sezione (in questo caso, essendo la trave rettangolare, y_max=h/2, il momento d’inerzia I_x =(bh³)/12 e conseguentemente W= (bh²)/6

Imponendo che il valore massimo di tensione (σ_max) sia pari al valore di progetto (f_d), posso determinare il valore minimo del modulo di resistenza a flessione della sezione (W_min) ed infine esplicitare il valore dell’altezza h, ottenendo la formula scritta poco sopra.

Dimensionamento trave in acciaio

Per il dimensionamento della sezione in acciaio, dobbiamo determinare il modulo di resistenza a flessione minimo da utilizzare affinché la tensione del materiale non superi la tensione di progetto. Sintetizzando: dati f_yd e M_max (calcolato precedentemente), ricaviamo W_x,min.

f_yd (f_d nel file Excel) è la tensione di progetto e si calcola a partire dalla tensione caratteristica di snervamento dell’acciaio prescelto e dividendola per un coefficiente di sicurezza γ_s pari a 1,05 (schiacciante il confronto con il coefficiente di sicurezza del legno).

F_yd = F_yk/ γ_s

Scegliamo un acciaio Fe 430/S275, con una tensione di snervamento caratteristica di 275 MPa. Inserendo il valore di f_yk, il file Excel mi calcola direttamente il W_x,min.

W_x,min = M_max/f_yd

Anche qui, il modulo di resistenza a flessione minimo lo abbiamo ricavato partendo dalla formula di Navier per la flessione (vedi quanto scritto per il dimensionamento della trave lignea).

Essendo stato effettuato il calcolo considerando lo stato limite ultimo (fd = σ_max), W_x,min è il valore minimo(affermazione leggermente tautologica, d’accordo) che posso scegliere per il dimensionamento. Dovrò, come sempre, ingegnerizzare i risultati ottenuti. Avendo ottenuto quindi un W_x,min = 485,51 cm3, sceglierò una IPE300 con W_x = 557,1 cm3.

Trave in calcestruzzo armato con sezione rettangolare

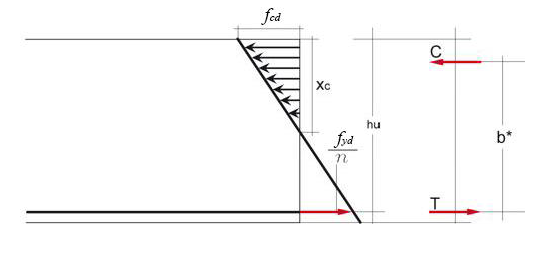
Infine, la trave in calcestruzzo armato. In questo caso i dati del progetto sono i valori delle tensioni di progetto del cls (f_cd) e dell’acciaio (f_yd), nonché la base, il Momento massimo e δ (la distanza tra il baricentro dell’armatura inferiore ed il filo del cls teso, che imponiamo uguale a 5cm).

Iniziamo scegliendo il tipo di acciaio ed il tipo di calcestruzzo che utilizzeremo, determinando prima f_yk ed f_ck (le resistenze caratteristiche dell’acciaio e del calcestruzzo), poi f_cd e f_yd (le tensioni di progetto del calcestruzzo e dell’acciaio)

f_yd = f_yk/ γ_s             f_cd = α_cc(f_ck/ γ_c)

γ_s  è il coefficiente parziale di sicurezza relativo all’acciaio (pari a 1,15), α_cc è il coefficiente riduttivo per le resistenze di lunga durata (0,85) e γ_c il coefficiente parziale di sicurezza relativo al cls, pari a 1,5.

Scegliamo un acciaio B450A (con f_yk = 450 MPa) ed un calcestruzzo ordinario C 25/30 (f_ck = 30 MPa)

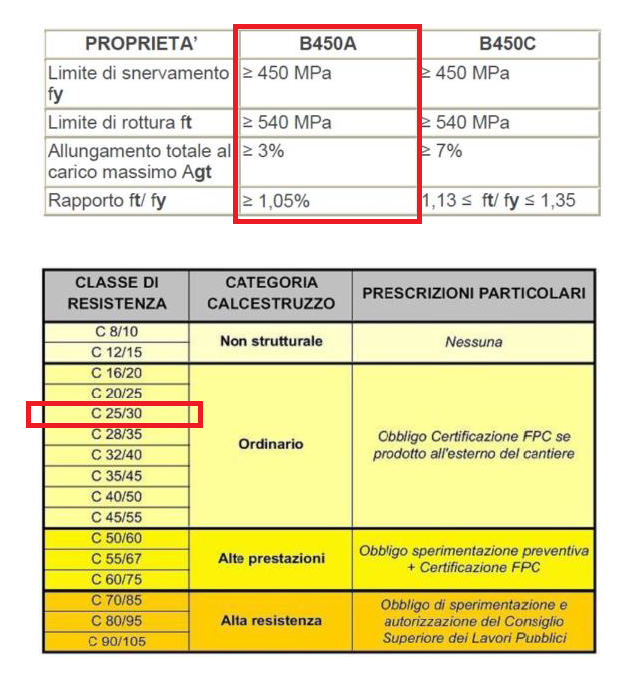
Definendo quindi la base della nostra sezione (30cm) e noti i valori delle tensioni di progetto, determiniamo h_u (l’altezza utile della sezione, pari all’altezza totale meno δ), da cui poi otterremo appunto una H_min (altezza minima della sezione).

H_min = h_u + δ

h_u = r(M_max/b)^0.5    con r = (2/[f_cd*(1-β/3)* β])^0.5      e     β= f_cd/(f_cd+f_yd/n)

L’altezza minima andrà poi ingegnerizzata in eccesso. Nel nostro caso quindi, ottenendo una h_u = 33,41 cm avremo una H_min= 38,41cm, che ingegnerizziamo prendendo un’altezza H = 45cm.

 

A questo punto, a differenza dei due casi precedenti con la trave in legno o in acciaio, dovremo fare nuovamente i calcoli aggiungendo al carico totale qu il peso proprio della trave (il peso specifico del cls armato è pari a 25kN/m³, che dovrà esser moltiplicato per il volume), moltiplicato per un fattore di sicurezza pari a 1,3. Se l’altezza minima risultante sarà ancora minore dell’altezza ingegnerizzata da noi scelta, la sezione risulterà verificata anche una volta aggiunto il peso proprio della trave (si veda quindi che, qualora fosse stata scelta un’altezza pari a 40cm – comunque maggiore della h_u,min, la sezione non sarebbe stata verificata una volta aggiunto il peso proprio; si è dovuto quindi ricorrere ad una H maggiore, pari appunto a 45cm).

L’esercitazione è finita, vorrei spendere solo alcune righe per spiegare in maniera molto sintetica (proponendo solo alcuni passaggi i concetti fondamentali alla base delle formule utilizzate per calcolare l’altezza utile minima della sezione in calcestruzzo.

Le ipotesi di progetto sono la conservazione delle sezioni piane e che entrambi i materiali attingano contemporaneamente la tensione di progetto. Queste ipotesi ci permettono di sfruttare la legge di Hooke (σ = E*ε) ed impostare una proporzione tra allungamenti, deformazioni e tensioni.

Una delle caratteristiche fondamentali del calcestruzzo armato è la non omogeneità del materiale (si parla di tre materiali: acciaio, calcestruzzo compresso e calcestruzzo teso). Risulta necessario operare un procedimento di omogeneizzazione tra le tensioni presenti nell’acciaio e quelle presenti nel calcestruzzo (mettendole in rapporto tra di loro), rapporto che viene infine ridotto a quello tra i rispettivi moduli elastici (E_f/E_c), pari a 10 e portato a 15, in quanto il modulo elastico del calcestruzzo diminuisce con il passare del tempo (n=15).

Potremo quindi scrivere σf =n σc

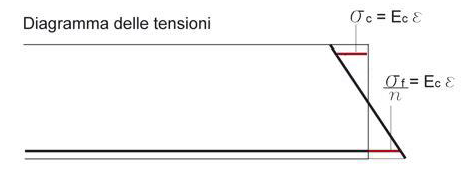
Avremo quindi un diagramma delle sollecitazioni di questo genere:

Ora, per progettare la sezione, posto σ_f =  f_yd  e σ_c = f_cd , dobbiamo ricavare la distanza X_c tra il lembo superiore compresso e l’asse neutro (non coincidente con quello geometrico). Per far questo, impostiamo un’eguaglianza tra triangolo (dividendo f_yd per n).

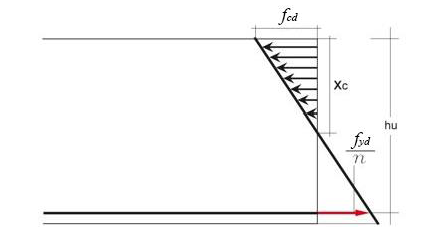
Noto X_c (che esprimiamo in funzione di h_u), sappiamo che il momento flettente esterno è dato da una coppia interna che vede la compressione sul calcestruzzo e la trazione sull’acciaio. Ponendo il centro di rotazione in T, calcoliamo il Momento M=C*b* (con b*=h_u – X_c/3 e C=(f_cd*b*X_c)/2), possiamo infine esplicitare il valore minimo dell’altezza utile h_u.