blog di Giorgio.Azzariti

Ci proponiamo, con la seguente esercitazione, ci calcolare come viene ripartita una forza orizzontale (come ad esempio quelle derivanti dal sisma o dal vento) sui diversi telai che compongono la nostra struttura, applicando il metodo delle rigidezze per mezzo del foglio Excel da voi fornito.

Iniziamo innanzitutto disegnando la pianta strutturale dell’edificio preso come riferimento.

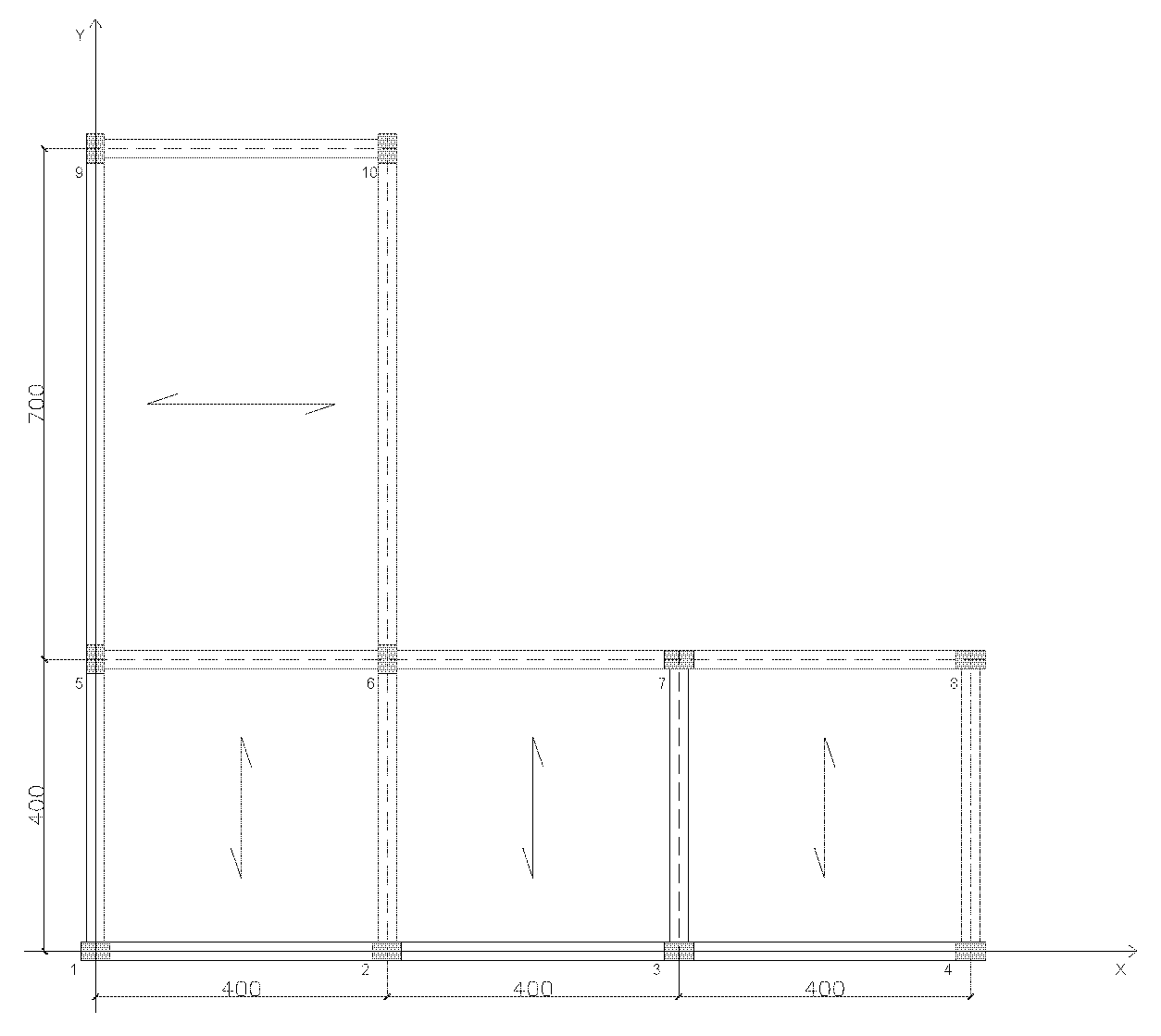
Prenderemo in considerazione un generico edificio ad un solo piano con struttura composta da telai piani (ossia un insieme di travi e pilastri allineati sopra un piano verticale) in cemento armato. Questi, oltre a trasmettere i carichi verticali alle fondazioni, possono svolgere anche il ruolo di controventi. E’ bene precisare che, perché un sistema di controventamento possa essere efficace, bisogna trovarsi nella situazione in cui gli impalcati possono essere considerati corpi rigidi sul proprio piano (al di quale si inflettono), per cui la forza orizzontale loro applicata tende a spostarli, ed i controventi contrastano questa azione grazie alla loro elasticità.

Oltre ad una specifica in termini di tecnologia utilizzata (quella del cemento armato, appunto), bisogna altresì premettere che questa esercitazione è dedicata anche ad una specifica tipologia di controventi, ossia i telai shear-type. Non essendo argomento specifico dell’esercitazione, non ci dilungheremo né sul concetto di rigidezza, né su quello di telaio shear-type. Basti ricordare che si tratta di un telaio con tutti nodi ad incastro e con la trave considerata infinitamente rigida flessionalmente rispetto ai pilastri. Confrontando un telaio di questo tipo con un altro con – ad esempio – traverso flessibile, ci rendiamo immediatamente conto della forte differenza in termini di rigidezza: il telaio shear-type è otto volte più rigido. Trattasi – ovviamente – di modelli, astratti quindi dalla realtà, ma accettati in quanto – associandoli appunto alla tecnologia del cemento armato – ne approssimano alcune caratteristiche.

Torniamo alla nostra struttura. In pianta si possono individuare sette telai, quattro paralleli all’asse y e tre paralleli all’asse x

Telaio 1v_erticale, composto dai Pilastri 1,5,9

Telaio 2v_erticale, composto dai Pilastri 2,6,10

Telaio 3v_erticale, composto dai Pilastri 3,7

Telaio 4v_erticale, composto dai Pilastri 4,8

Telaio 1o_rizzontale, composto dai Pilastri 1,2,3,4

Telaio 1o_rizzontale, composto dai Pilastri 5,6,7,8

Telaio 1o_rizzontale, composto dai Pilastri 9,10

 

Detto ciò, cambiamo “abito mentale”, passando a vedere l’impalcato come un corpo rigido dotato di massa ed i controventi come molle che lo vincolano impedendogli di spostarsi eccessivamente. I controventi, che per il telaio rappresentano vincoli cedevoli elasticamente, possono essere schematizzati infatti come molle, aventi un’adeguata rigidezza.

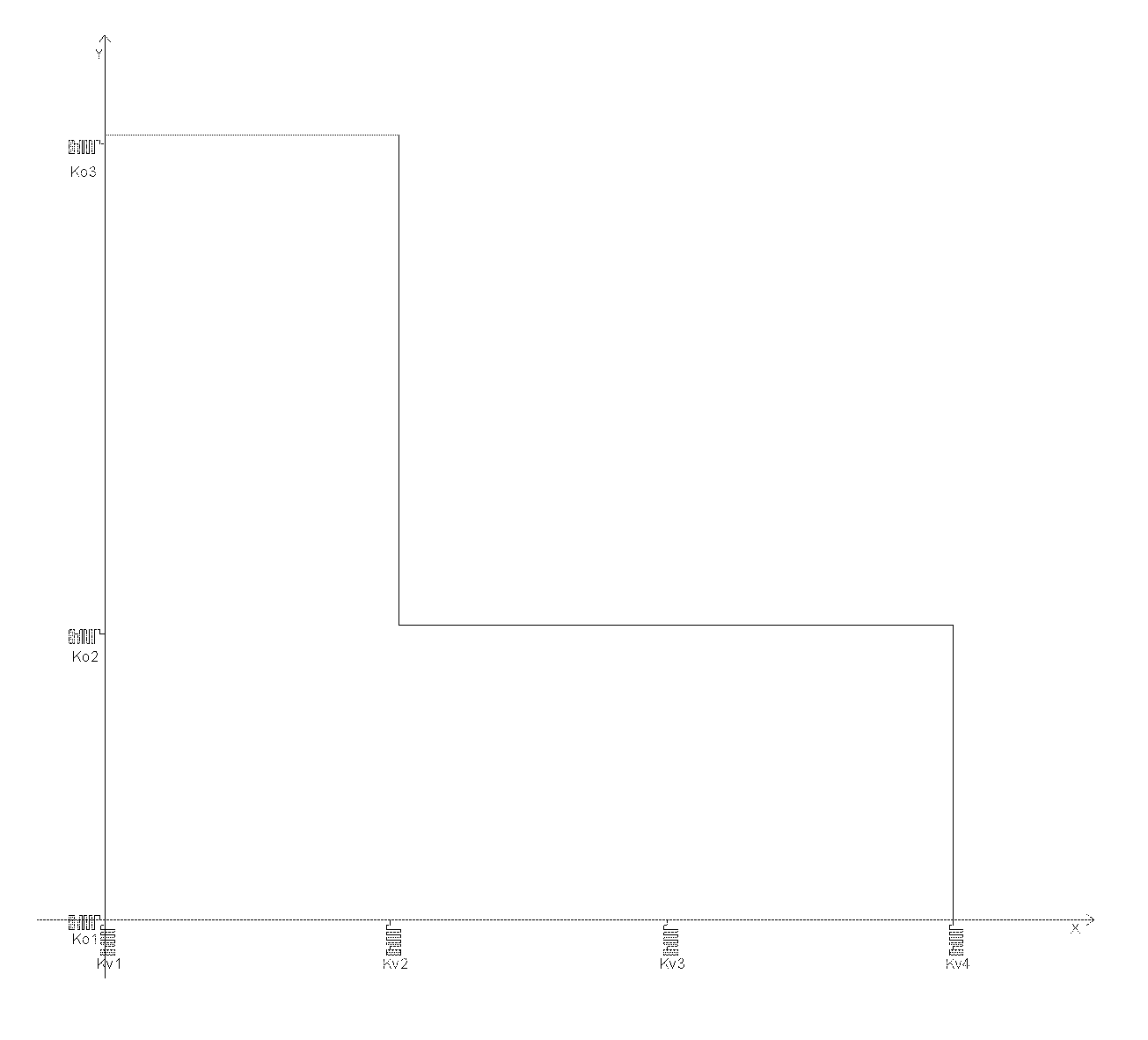
Entrando nel vivo dell’esercitazione, iniziamo calcolando le rigidezze traslanti dei controventi dell’edificio. Ipotizzando, come già accennato, che il solaio sia rigido a sufficienza da considerare la struttura composta da telai Shear-Type, possiamo passare a calcolarci la rigidezza traslante K_T (KN/m) di ogni telaio, ovvero la somma delle rigidezze dei singoli pilastri che la compongono

K_telaio= (12E/h³) x

Ricordandoci che il telaio di tipo Shear-Type ha una rigidezza pari a:

k= 12EI/h³

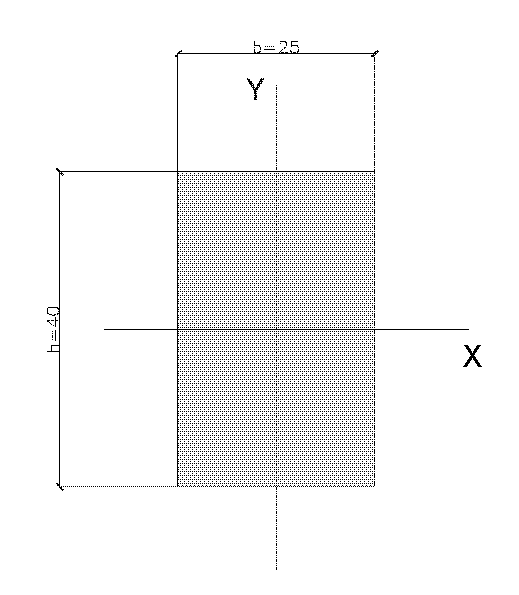
Una volta definita la nostra sezione e tenuto conto della disposizione dei pilastri in pianta, con:

E= Modulo di Young = 21000 N/mm²

H= altezza = 3,2 m

I_x= Momento d’Inerzia parallelo all’asse x = bh³/12 =

133 333,3 cm⁴

I_y= Momento d’inerzia parallelo all’asse y = b³h/12 =

 52083,3 cm⁴

Avremo quindi:

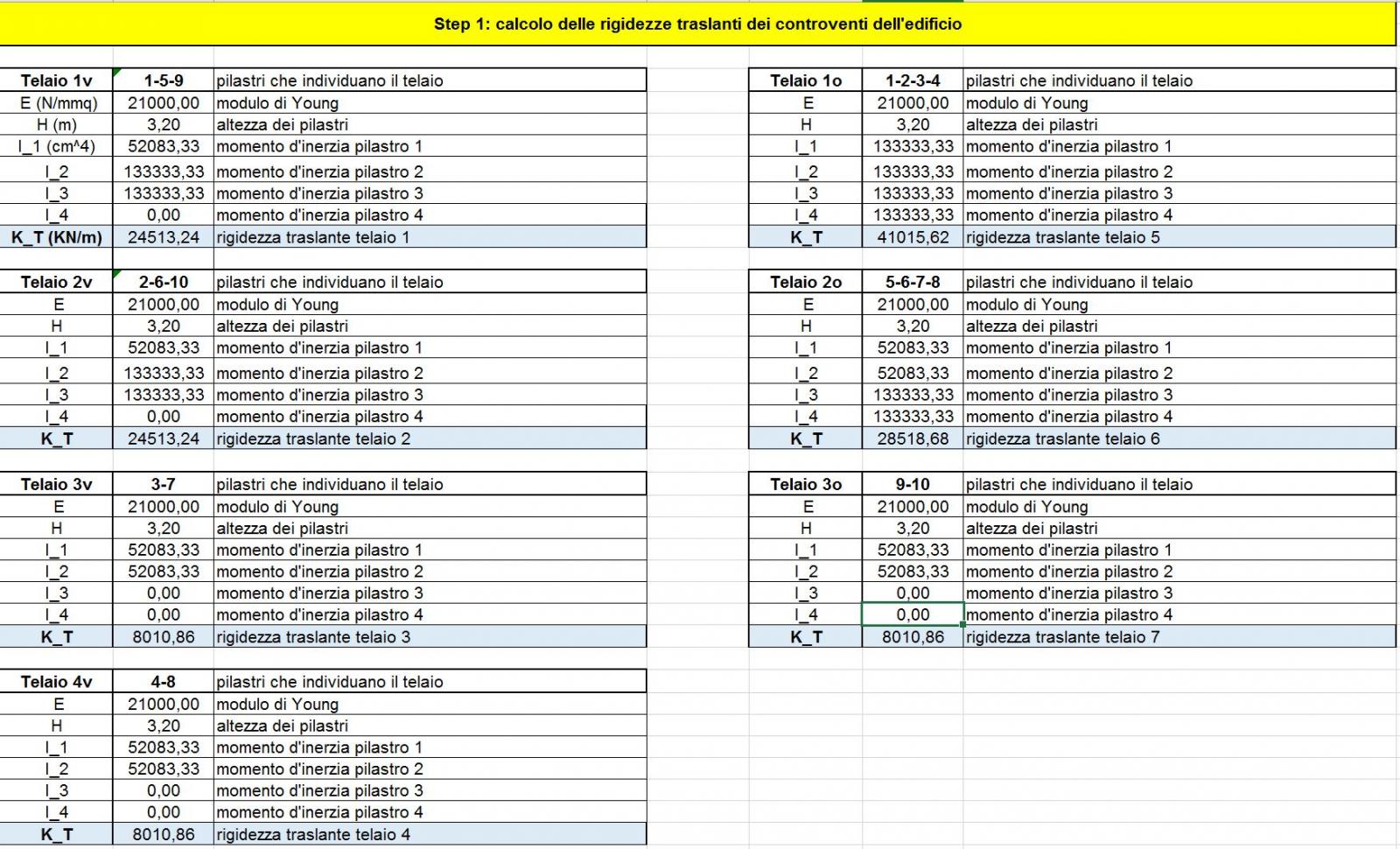
Nella tabella sinottica dei controventi e delle distanze riportata di sotto, oltre ad essere riassunte le diverse rigidezze di tutti i controventi, vengono anche riportate le distanze dei diversi controventi dal punto O, origine di un sistema di riferimento da noi scelto (a tal proposito, ci riferiamo all’immagine dell’impalcato inteso come corpo rigido dotato di massa ed i controventi come molle, dove sono riportate le distanze dei controventi dall’origine).

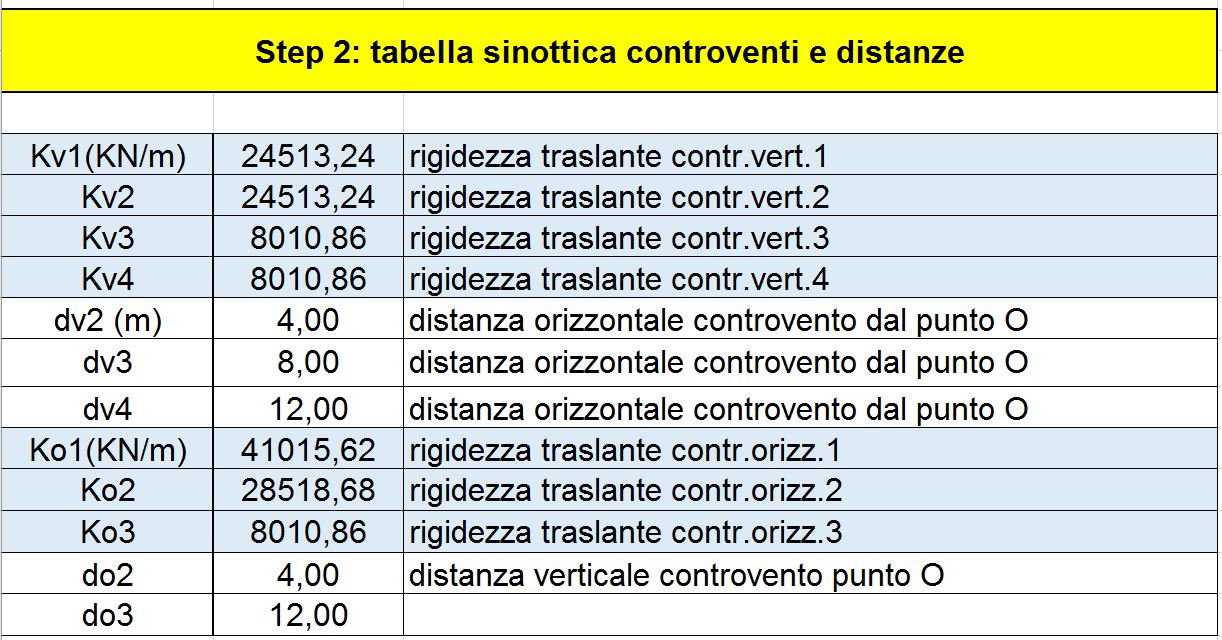
Passiamo quindi a calcolare il Centro di Massa ed il Centro di Rigidezza dell’impalcato. Entrambi i procedimenti sono figli dello stesso concetto base, ossia il metodo attraverso cui ottenere il centro di un sistema di vettori paralleli. Tralasciando per sinteticità dell’esercitazione la dimostrazione, basti sapere che lo stesso procedimento viene poi declinato a seconda del “centro richiesto”: nel caso del centro delle rigidezze, le variabili saranno, oltre alla rigidezza totale, la distanza dei controventi dal centro delle rigidezze; nel caso del Centro di massa (coincidente con il centro d’area, qualora la densità di massa dell’impalcato sia uniforme su tutto l’impalcato), oltre all’area, la distanza dei centri d’area delle figure geometriche elementari dall’origine del nostro sistema di riferimento.

Incominciamo quindi calcolandoci quest’ultimo. Per semplicità, suddividiamo l’impalcato in due figure geometriche elementari (due rettangoli) ed indichiamo il centro di massa e l’area di ognuna di queste due figure. Ciò fatto, ipotizziamo appunto che la densità di massa dell’impalcato sia uniforme lungo tutto quest’ultimo.

 

Le coordinate del centro di massa saranno:  

x_G = (Σ_i=1->nAi*xGi)/ A_tot

y_G = (Σ_i=1->nAi*yGi)/ A_tot

Qualora l’ipotesi di densità uniforme dell’impalcato non fosse valida, il centro di massa non coinciderebbe con il centro d’area e dovremmo quindi ricorrere alla variabile “Massa”:

x_G = (Σ_i=1->nMi*xGi)/ A_tot

y_G = (Σ_i=1->nMi*yGi)/ A_tot

 

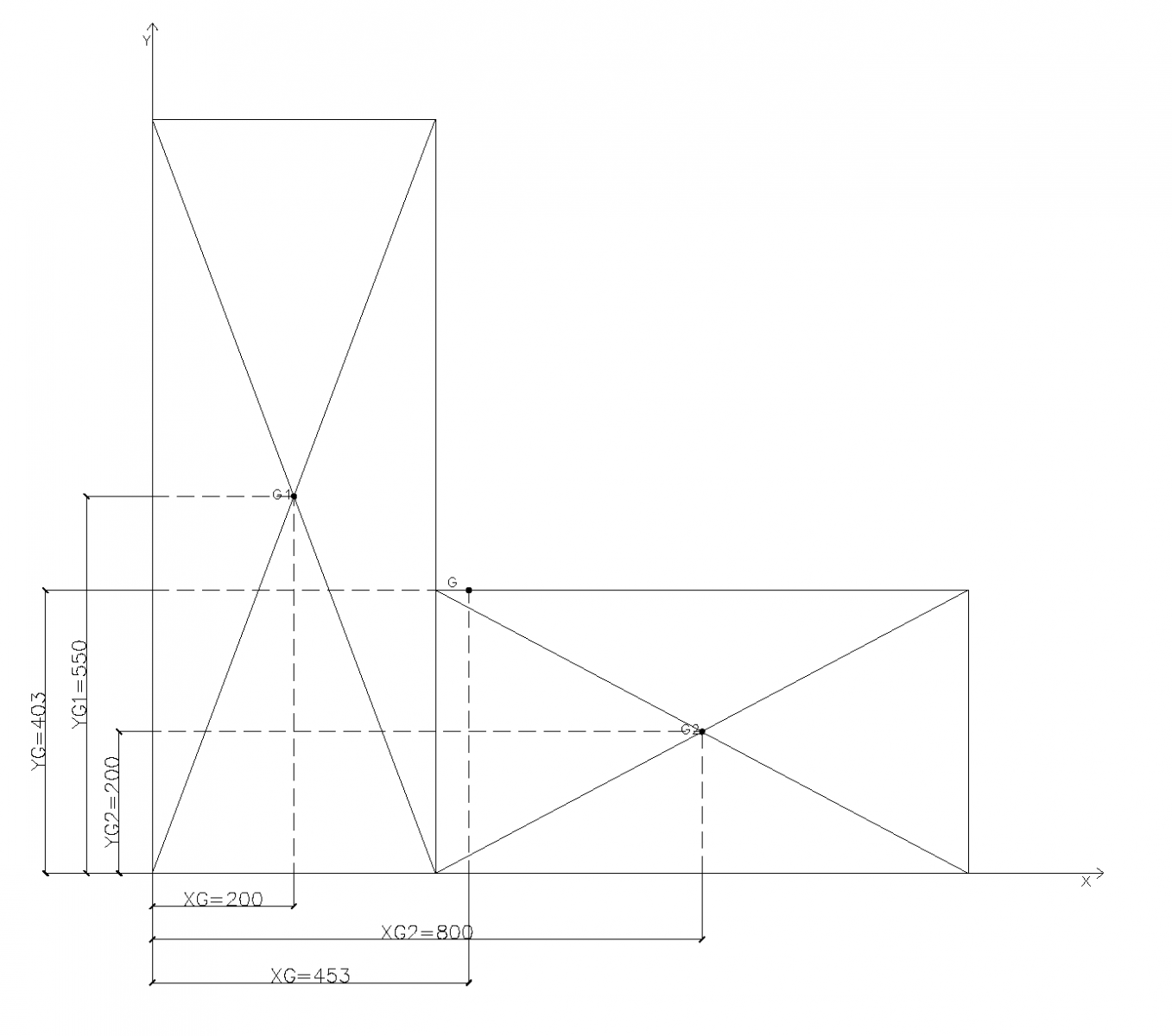
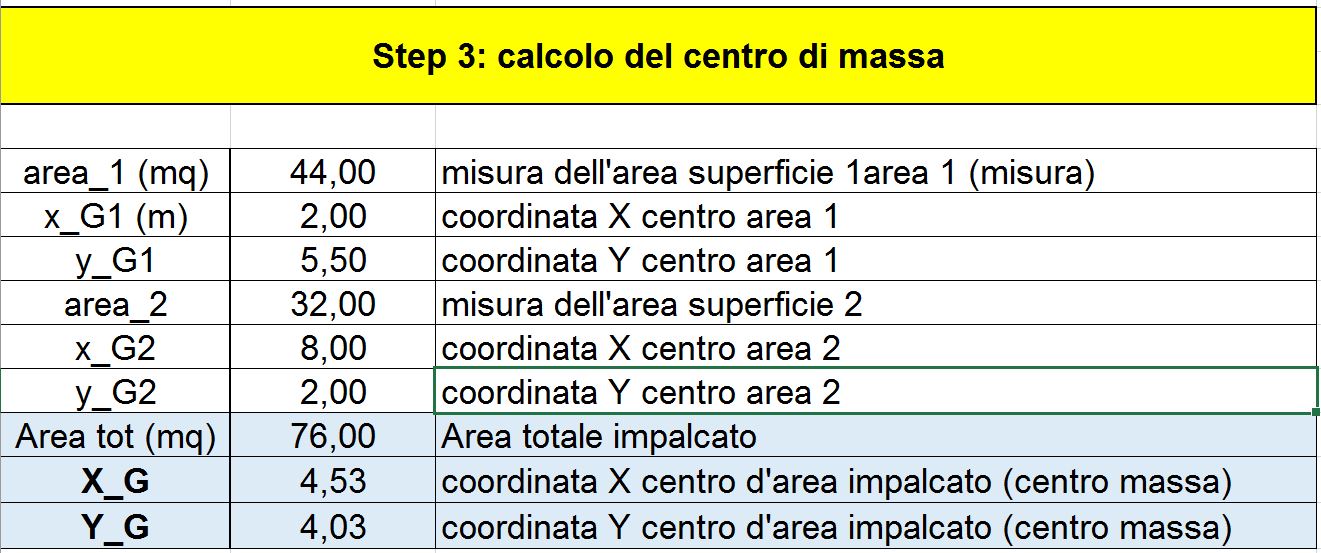
Procedimento analogo per quanto riguarda il Centro delle Rigidezze dell’impalcato. Le coordinate del centro di rigidezza, formalmente analoghe alle coordinate del centro di massa, sono:

x_G = (Σ_i=1->nKvi*Dvi)/ K_{v_tot}

y_G = (Σ_i=1->nKoi*Doi)/ K_{o_tot}

 

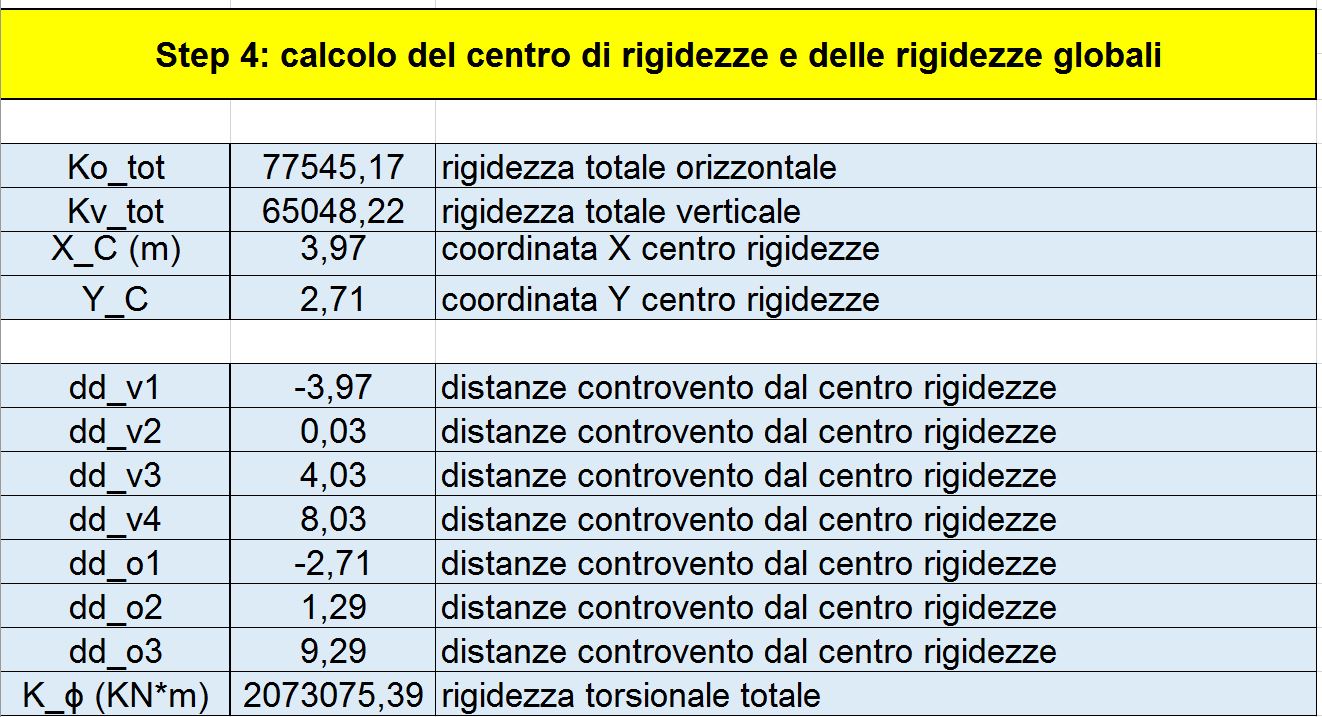
Abbiamo quindi posizionato il centro di massa ed il centro delle rigidezze all’interno del sistema di riferimento in cui abbiamo disegnato l’impalcato (ricordiamoci difatti che – ai fini di quest’esercitazione – la forza sismica viene applicata nel centro di massa G).

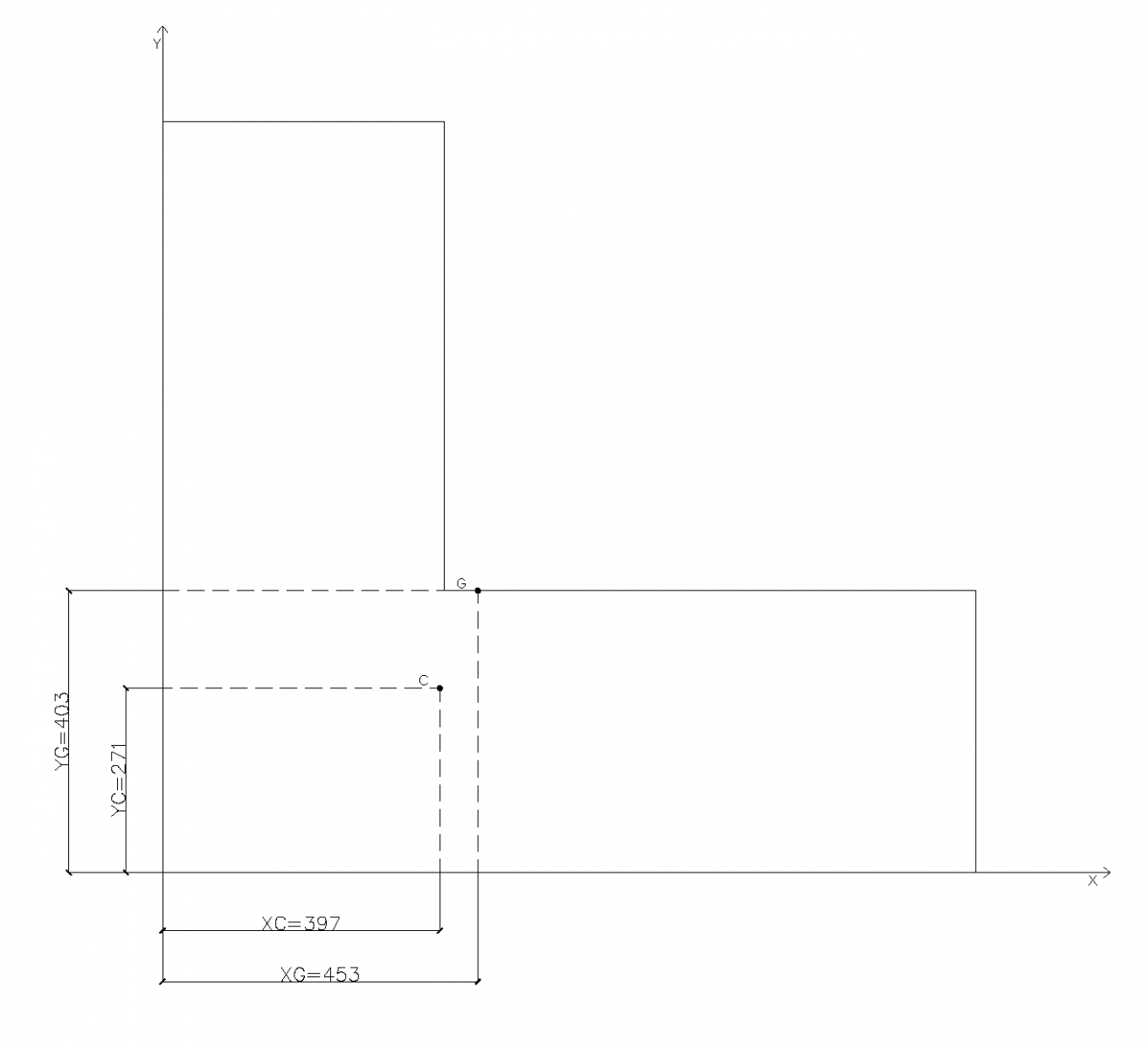
Non coincidendo i due (ossia, poiché la retta d’azione della forza esterna – applicata nel centro di massa - non passa per il centro delle rigidezze), l’impalcato è soggetto a traslazione e rotazione; si produrrà quindi uno spostamento sull’asse in cui è applicata la forza ed un momento che farà ruotare l’impalcato con perno nel centro delle rigidezze e braccio pari alla coordinata che informa sulla distanza di questa forza dal centro delle rigidezze.

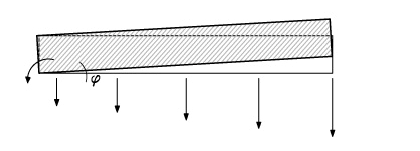
Schematizzando quanto detto in maniera semplice, ci troveremo innanzi ad una situazione analoga a quanto riportato nelle due successive immagini:

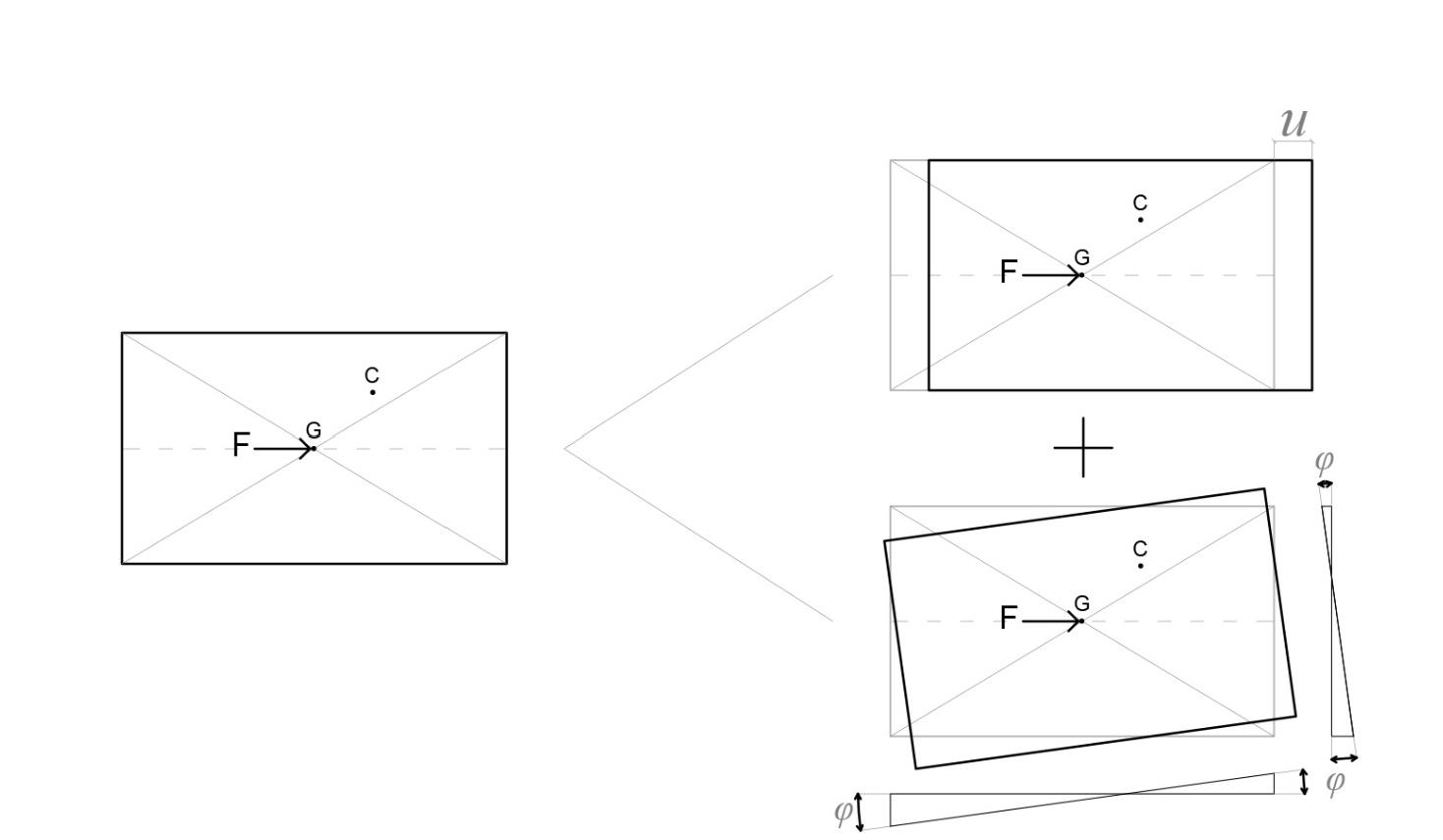
Rotazione e spostamento dettati da una forza applicata orizzontalmente

 

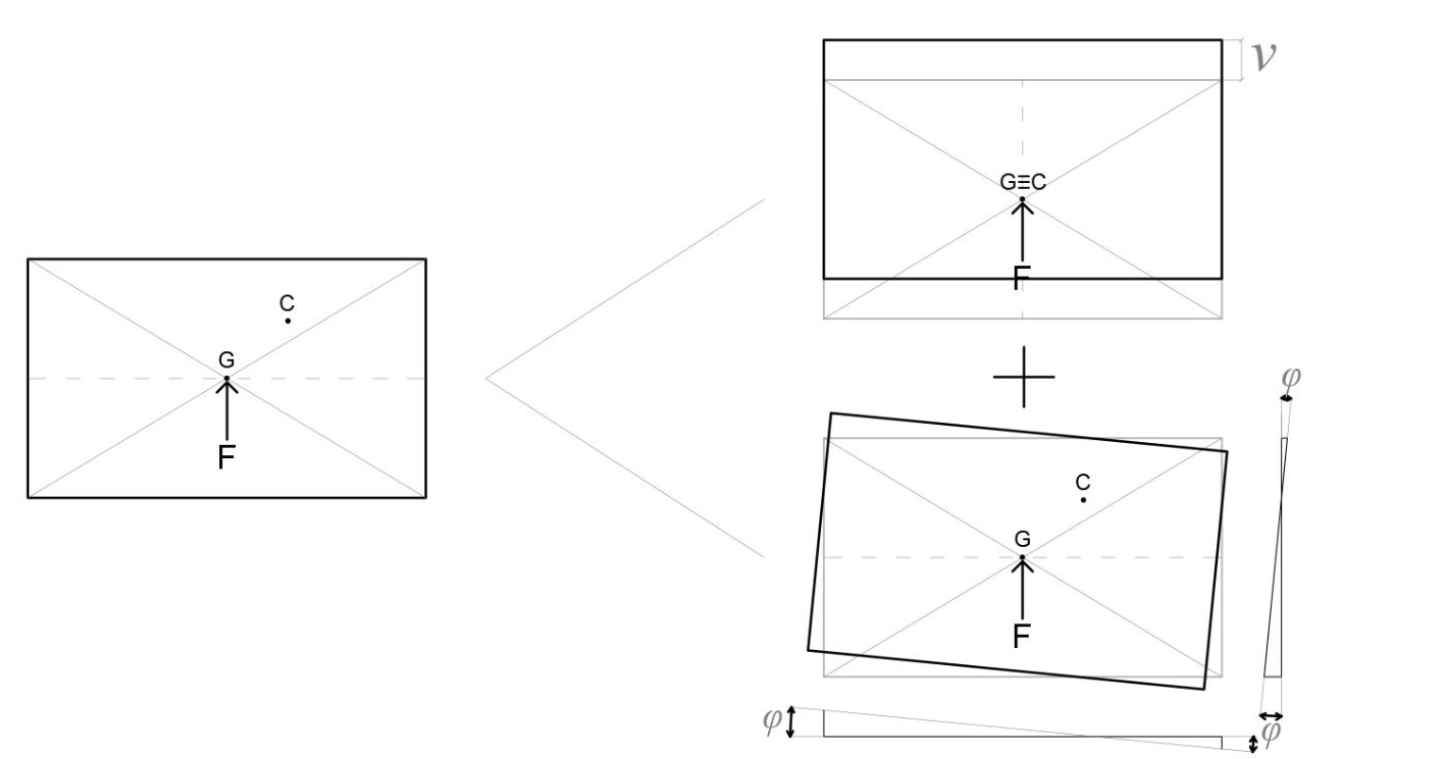
Rotazione e spostamento dettati da una forza applicata verticalmente.

Nella tabella precedente, oltre a calcolare le coordinate del centro di rigidezza, ricaviamo anche il valore della rigidezza torsionale K_Φ, ossia la sommatoria di tutte le rigidezze dei controventi (calcolate nel primo passaggio) moltiplicate per la loro distanza dal centro delle rigidezze. Questa rigidezza torsionale servirà in seguito – come vedremo – per il calcolo della rotazione dell’impalcato secondo una direzione.

K_Φ =Σ_i=1->nK_vi*dd²_vi + K_oi*dd²_oi

 

Manca ora il calcolo della forza sismica che agisce nel centro di massa: conditio sine qua non, l’analisi dei carichi sismici, ergo il carico totale permanente G ed il carico totale accidentale Q.

Ipotizziamo il solaio latero cementizio seguente:

Il carico totale permanente G sarà uguale a G = (q_s + q_p)*A_tot

Il carico totale accidentale, invece Q = q_a*A_tot

Introduciamo quindi il carico sismico W = G + Q*ψ

con ψ equivalente al coefficiente di contemporaneità, il cui valore è fornito dalla normativa; nel nostro caso, ipotizziamo una categoria A (ambienti ad uso residenziale), con quindi una fattore ψ=0,3:

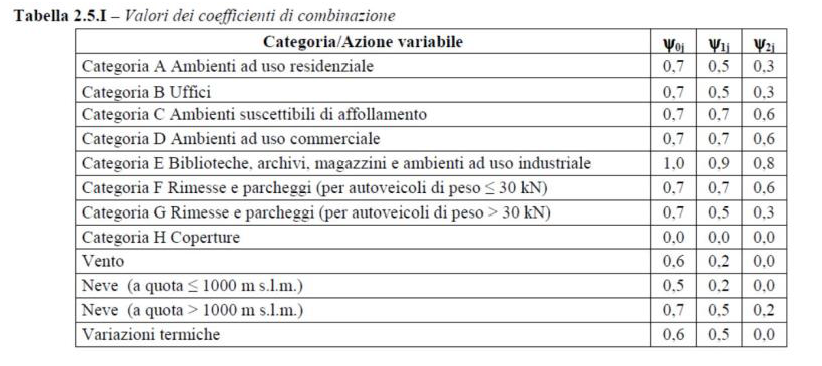
Il peso sismico W, espresso in kN, rappresenta la forza peso dell’edificio, data dal prodotto tra la massa dell’edificio e l’accelerazione di gravità. Poiché il sistema ha un’accelerazione mediamente più piccola dell’accelerazione di gravità, può essere introdotto un coefficiente di intensità sismica c, che tenga conto della sismicità del luogo di progettazione dell’edificio

F=W*c

Nel nostro caso, c=0,1

Ci stiamo quindi avviando alla conclusione. Si dovrà ora quantificare la ripartizione della forza sismica F lungo l’asse x e lungo l’asse y (nello specifico, per ognuno dei diversi controventi). Detto altrimenti, arriviamo infine a calcolare il valore degli spostamenti u, v e Φ.

Lo spostamento orizzontale, u, sarà pari ad u = F/(k_{o_tot})

Lo spostamento verticale, che chiamiamo v, sarà pari a v = F/(k_{v_tot})

Infine, la rotazione Φ impressa all’impalcato sarà uguale a Φ=M/k_Φ

Una volta determinato il valore dei gradi di libertà, possiamo ricavare la forza sui singoli controventi nei due casi di carico.

Quando la forza è parallela all’asse x, la reazione elastica dei controventi orizzontali sarà pari a:

F_{o_n}= k_{o_n} (u+Φ*dd_{o_n})

Mentre in quelli verticali:

F_{v_n}=k_{v_n}* Φ*dd_{v_n}

Quando invece la forza è parallela all’asse y, la reazione elastica dei controventi verticali sarà:

F_{v_n}=k_{v_n}(v+ Φ*dd_{v_n})

Mentre in quelli orizzontale sarà

F_{o_n}=k_{o_n}* Φ*dd_{o_n}

Intuitivamente, poiché il corpo non si limita a traslare, per poter conoscere il valore della rotazione, bisognerà calcolare il Momento Torcente M dell’asse x, moltiplicando la forza sismica F per il suo braccio, ovvero la differenza tra l’ordinata del centro delle rigidezze e quella del centro di massa, e per l’asse y, utilizzando come braccio la differenza tra le ascisse dei due centri. Infine, si calcola la traslazione orizzontale, dividendo F per la rigidezza traslante orizzontale, la traslazione verticale, dividendo F per la rigidezza traslante verticale, e le rotazioni, dividendo i rispettivi Momenti torcenti per la rigidezza rotazione K Φ.

L’esercitazione è così conclusa. Vorrei ora spendere alcune righe per spiegare in maniera molto sintetica come siamo arrivate alle formule scritte poco sopra.

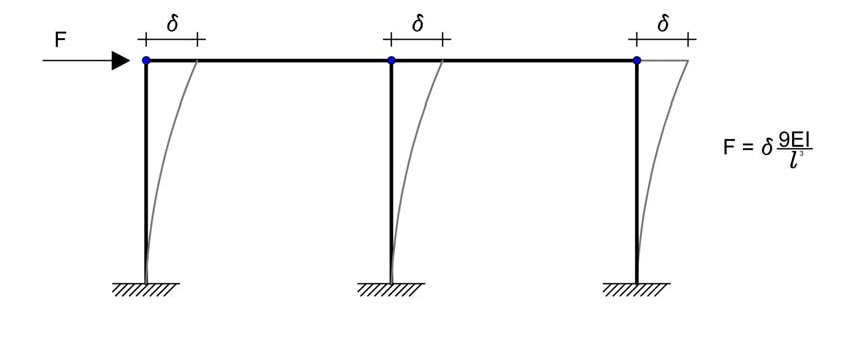
Astraiamoci dal caso specifico ed immaginiamo un sistema iperstatico come quello riportato nella figura sottostante

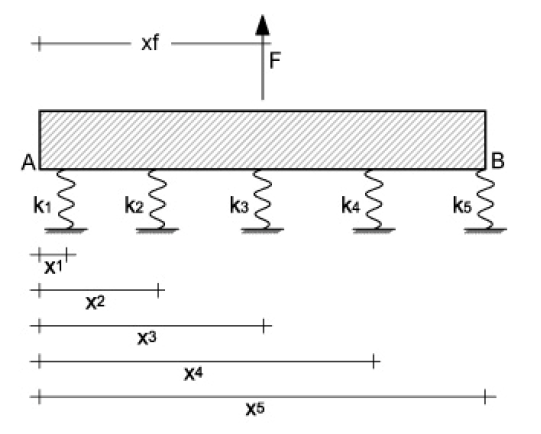
Dato che il corpo è rigido e piano, la cinematica dipende solamente da tre parametri:

la traslazione orizzontale δ_o, la traslazione verticale δ_v e la rotazione Φ.

Per determinare le tre incognite, si ipotizza un parametro di spostamento per volta, registrando le azioni nelle molle che questo produce; poi, invocando il principio di sovrapposizione degli effetti, in ogni molla si somma il contributo dovuto ad ognuno dei tre parametri. In conclusione, si scrivono le tre equazioni di equilibrio e si ricavano i valori dei tre parametri.

Nel caso in figura, non ci sono né forze né molle orizzontale, di conseguenza δo=0.

Le incognite da determinare sono quindi δv e la rotazione Φ. Gli effetti che essi inducono sulle reazioni vincolari elastiche sono i seguenti:

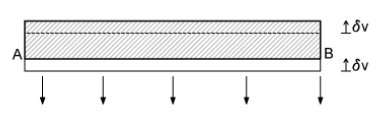
Con Ri₁ = -ki δv

Con Ri₂=-ki δv Φxi

Applicando il principio di sovrapposizione degli effetti, avremo R= Ri₁ + Ri₂

Sinteticamente: vado a scrivere le equazioni di bilancio alla traslazione verticale ed alla rotazione. Se il punto O attorno al quale abbiamo scelto di far agire Φ ed effettuato il bilancio dei momenti è pari a C, la soluzione sarà immediata, arrivando così alle formule applicate precedentemente.

Noti δo, δv e Φ, posso determinare le reazioni elastiche di ogni controvento.

Pur presentando una carpenteria differente rispetto a quella proposta nella precedente esercitazione (mantenere le stesse dimensioni per verificare le diverse esigenze in termini di geometria della sezione rispetto alle due diverse verifiche sarebbe stato interessante qualora la struttura isostatica proposta fosse stata la stessa; in questo caso, tuttavia, ci troviamo di fronte ad una mensola, non più di fronte ad una trave appoggiata-appoggiata), riproporrò gli stessi solai (in legno, acciaio e calcestruzzo armato) e gli stessi materiali (legno Gl 24c, acciaio Fe 430/S275, calcestruzzo C 25/30 con barre d’acciaio B450A) riprendendo quindi alcuni dati e modificandone altri. 

 

Lo scopo della terza esercitazione è quello di effettuare su queste tre mensole, da non confondere con aggetti, la verifica a deformabilità, controllando l’abbassamento minimo dell’elemento strutturale in rapporto alla sua luce. A proposito di mensole ed aggetti, cercherò di dare una definizione empirica della differenza tre le due: la geometria delle prime “termina” nel momento in cui entra in contatto con la parete o il pilastro che la sostiene (mettendo gli occhiali della cinematica, diremmo dell’incastro); i secondi, invece, continuano. Detto altrimenti, mentre le mensole sono corpi “interamente” a sbalzo, gli aggetti ne presentano solo una parte.

Il procedimento è analogo (seppur con alcune differenze che vedremo) per tutte e tre le tecnologie, e da effettuarsi allo Stato Limite d’Esercizio (SLE), differentemente da quanto avvenuto invece per il dimensionamento delle travi nella precedente esercitazione, che ha avuto luogo allo Stato Limite Ultimo (SLU). La motivazione è chiara: il tipo di verifica che ci interessa - in questo caso - non è finalizzata ad esser sicuri o meno che la struttura non si “rompa”; ci si pone un gradino sotto, controllando che non vi siano spostamenti che possano limitare l’uso della costruzione, la sua efficienza ed il suo aspetto. Torniamo quindi con un concetto già accennato nella prima esercitazione a proposito delle due fondamentali operazioni di verifica da applicare sulle strutture: le prime di carattere fondamentale (la verifica a rottura allo SLU), che pongono in gioco questioni vitali riguardo la rottura della struttura e la salvaguardia stessa della vita umana; le altre inerenti al benessere (la verifica a deformabilità allo SLU).

Ipotizziamo in tutti e tre i casi di trovarci dinnanzi ad una mensola di lunghezza l e caricata con un carico uniformemente distribuito pari a q_u. Evidentemente, il momento massimo – in corrispondenza della sezione d’incastro – varrà

M_max=(q_u*l²)/2

L’importanza nel sottolineare il tipo di carico (distribuito o concentrato) nonché – nel caso di carico distribuito – il tipo di distribuzione (uniforme o non) è cruciale: questo condiziona il momento massimo che a sua volta influenza lo spostamento minimo (insieme ad altri fattori che vedremo in seguito: il Modulo Elastico ed il Momento d’Inerzia).

Entriamo quindi nel vivo della terza esercitazione.

Nell’aprire il file Excel ci troviamo di fronte – nella parte inziale – ad un qualcosa di già visto nell’esercitazione numero due (eccezion fatta per il valore del momento massimo nella sezione maggiormente sollecitata; del resto stavamo prendendo in considerazione una trave doppiamente appoggiata). Iniziamo quindi con il ricavarci, con un procedimento analogo a quello già applicato in precedenza (per una descrizione dettagliata di tutti i passaggi riferirsi quindi alla suddetta esercitazione), la geometria delle nostre mensole, attraverso il calcolo dell’altezza minima (nel caso del legno e del calcestruzzo armato) oppure del modulo di resistenza a flessione minimo (nel caso dell’acciaio).

Per un interasse di 4,5m ed una luce di 3m, con le caratteristiche dei materiali precedentemente descritti, otterremo una sezione lignea di 30x60, una IPE300 ed una sezione in calcestruzzo armato 30x50 (ovviamente dopo le necessarie ingegnerizzazioni). 

Legno

Acciaio

Calcestruzzo armato

 

Quindi, dopo aver dimensionato le sezioni allo SLU, possiamo verificarne la deformabilità allo SLE. Ed è proprio poiché questo tipo di verifica (per motivazioni introdotte prima) viene fatto allo stato limite d’esercizio che i carichi incidenti sulla struttura vengono ricombinati seguendo la combinazione frequente, generalmente impiegata per gli stati limite di esercizio reversibili:

q_e= (G1 + G2 + ψ_11*Q₁) _* i con

G1 = rappresenta il valore caratteristico del peso proprio di tutti gli elementi strutturali (sostanzialmente q_s);

G2= il valore caratteristico del peso proprio di tutti gli elementi non strutturali (q_p);

ψ₁₁ = coefficiente che definisce il valore frequente dell’azione variabile Q1, assimilabile al valore medio della distribuzione temporale dell’intensità (pari nel nostro caso a 0,5);

 

Q₁₌ il valore caratteristico dell’azione variabile (q_a);

i = interasse

Ma non si riduce a questo la differenza rispetto alla verifica allo SLU. Ad esempio: nel caso del legno (il materiale più leggero fra i tre) il peso proprio della trave viene trascurato, come avviene anche nel caso di verifica a rottura allo Stato Limite Ultimo. Tuttavia, non è così non solo per il calcestruzzo armato, ma anche per l’acciaio; si dovrà quindi inserire nel foglio di calcolo anche il suo di peso, in kN/m (la nostra IPE300 pesa 42,2 kg/m, ossia 0,42 kN/m circa). Per questi ultimi due materiali quindi, il peso proprio verrà preso in considerazione per ricavare il carico totale q_e.

Nel nostro caso specifico, i pesi delle strutture che bisogna aggiungere per trovare il carico totale q_e sono:

3,75 kN/m per il calcestruzzo;

0,42 kN/m per l’acciaio;

Infine, il calcolo dello spostamento. Come già accennato, abbiamo bisogno di altre due informazioni oltre al valore del momento massimo: una relativa al materiale di cui è composta la mensola (ossia il suo modulo di elasticità, brutalmente sintetizzabile come il rapporto tra la tensione e la deformazione), l’altra relativa alla sua geometria (il momento d’inerzia I_x).

Questi valori sono rispettivamente:

E_legno =   11600 N/mm²  è il modulo elastico medio parallelo (da utilizzare nel caso di verifiche allo stato limite d’esercizio), non il modulo elastico caratteristico (da utilizzare per verifiche allo stato limite ultimo;

E_acciaio = 200000 N/mm²

E_calcestruzzo = 25000 N/mm²

I_x,legno = 540000 cm⁴

I_{x, acciaio} = 8356 cm⁴

I_{x, calcestruzzo} = 312500 cm⁴

Noti questi valori, possiamo calcolarci lo spostamento (abbassamento) massimo di una mensola sottoposta a carico uniformemente distribuito:

 v_max= - (q_e*l⁴)/8_*E_*I_x

Nel nostro caso, gli spostamenti saranno pari rispettivamente a:

v_max,legno= 0,41 cm

v_max,acciaio= 0,898 cm

v_{max,calcestruzzo armato}= 0,24 cm

L’esercitazione si conclude verificando che il rapporto tra la luce della trave ed il suo spostamento massimo sia maggiore di 250, come imposto dalla normativa di base al tipo di elemento strutturale considerato: l/vmax dev’essere minore od uguale a 250. Nel nostro caso, i rapporti sono tutti e tre verificati.

l/ v_max,legno = 882,97

l/ v_max,acciaio = 334,022

l/ v_{max,calcestruzzo armato} = 1275, 38

Legno

Acciaio

Calcestruzzo armato

 

Vorrei adesso spendere alcune righe sul come siamo arrivati a formulare lo spostamento massimo di una mensola con carico uniformemente distribuito. Per ricavare lo spostamento di questo schema isostatico noto prendiamo come base la trave di Bernoulli descritta da tre gruppi di equazioni:

quelle di Bilancio (siamo in campo statico)

dN/ds + q1 = 0

dT/ds + q2 = 0

dM/ds + T + μ = 0

quelle di Congruenza (siamo in campo cinematico)

ε_(s) = dv/ds

γ_(s) = dv/ds – ϕ_(s)

χ_(s) = d ϕ/ds

quelle del legame costitutivo (che fanno da trait d’union tra il campo statico e quello cinematico)

N_(s) = E_*A_*ε(s)

M_(s) = E_*I_* χ(s)

Partiamo quindi operando un taglio virtuale di Cauchy sulla nostra mensola; l’equazione in funzione di s che descriverà l’andamento del momento lungo la mensola sarà:

M_(s)=-(q_*l²)/2 + q_*l_*s – (q_*s²)/2

A partire da questa otterremo lo spostamento verticale in funzione di s integrando l’equazione tre volte, passando per la curvatura e la rotazione:

χ_(s) = -(q_*l²)/2_*E_*I + (q_*l_*s)/E_*I – (q_*s²)/2_*E_*I

ϕ_(s)= -(q_*l²_*s)/2_*E_*I + (q_*l_*s²)/2_*E_*I – (q_*s³)/6_*E_*I +c₁

v_(s)= -(q_*l²_*s²)/4_*E_*I + (q_*l_*s³)/6_*E_*I – (q_*s³)/24_*E_*I +c_1*s + c₂

Il valore di v ci è noto a meno di due costanti, che otteniamo analizzando due condizioni al bordo. Essendoci un incastro come vincolo, avremo che:

ϕ₍₀₎ = 0

v₍₀₎ = 0

Conseguentemente, c₁ = 0 e c₂ = 0, mentre v_(s=l) = -(q_*l⁴)/8_*E_*I, con il segno meno in quanto abbassamento. c.v.d.

Terminiamo constatando che, cambiando tipologia di carico (passando quindi da un distribuito uniforme ad un concentrato al centro e nell’estremo sena vincoli), non necessariamente cambierà il valore del momento massimo nella sezione più sollecitata (nel primo caso rimarrà sempre M_max = (q_*l²)/2, mentre nel secondo varia: M_max = q_*l²), mentre varia lo spostamento massimo:

v_max = -(7_*q_*l⁴)/78_*E_*I            nel caso del carico concentrato al centro

 

v_max = -(q_*l⁴)/24_*E_*I                nel caso del carico concentrato nell’estremo libero

Entrambi i valori si ottengono con procedimento analogo a quello descritto sopra, partendo dall’equazione del momento lungo la mensola in funzione di s ed integrandola tre volte (dividendo i due campi 0 < s < l/2 e l/2 < s < l nel caso di carico concentrato al centro).

Verifichiamolo velocemente creando due nuovi file Excel.

Nel primo caso ipotizziamo un carico ql concentrato e centrato. La formula del M_max non varia, mentre varia quella dello spostamento. La verifica va comunque a buon fine.

Legno

Acciaio

Calcestruzzo Armato

Nel secondo ipotizziamo invece un carico ql concentrato nell’estremo non vincolato. Cambierà tanto la formula dello spostamento, quanto quella del momento massimo (nel caso del calcestruzzo, bisogna ricordarsi di cambiarla due volte, la seconda nel momento in cui viene aggiunto il peso proprio e verificata nuovamente la fattibilità della geometria scelta. Anche in questo caso, la verifica va comunque a buon fine.

Legno

Acciaio

Calcestruzzo armato

 

 

 

 

 

 

 

 

 

 

Con l’esercitazione che segue dimensioniamo, grazie al file Excel fornito, tre travi (rispettivamente in legno, acciaio e calcestruzzo armato) attraverso un metodo di progetto che pone la tensione massima nella trave pari alla tensione di progetto del materiale, definito dalla normativa (viene di conseguenza il fatto che la dimensione di ogni sezione – nel nostro caso l’altezza – ricavata sarà l’altezza minima da prendere in considerazione).

Parto impostando una pianta di carpenteria di un generico edificio (la cui struttura è composta da telai piani, ossia da travi che collaborano con i pilastri). Come da voi suggerito, ai fini dell’esercitazione ritengo il vincolo che il pilastro esercita sulle travi come quella dato da un appoggio semplice.

Individuo quindi la trave principale (ossia la trave posta perpendicolarmente rispetto ai travetti secondari) maggiormente sollecitata (quella con area d’influenza maggiore); nel nostro caso, l’area è pari a 25m², la trave ha una luce di 5m ed un interasse uguale, pari sempre a 5m.

Ipotizzo a questo punto tre solai diversi, rispettivamente in legno, acciaio e calcestruzzo armato.

Devo quindi trovare i diversi valori di carico agenti sul solaio (che esprimerò come densità di carico superficiale in kN/m²) e che mi consentiranno quindi di determinare il carico di progetto sulla trave (questa volta si tratterà tuttavia di una densità di carico lineare, espressa quindi in kN/m).

I carichi agenti sul solaio sono:

i carichi strutturali q_s, ossia i carichi dovuto al peso proprio di tutti gli elementi che svolgono una funzione portante. Nel caso di un solaio in calcestruzzo armato – ad esempio – il peso dei travetti, la soletta corroborante ma anche i mattoni forati;

i carichi permanenti q_p, ossia i carichi dovuto al peso di tutti quegli elementi che gravano sulla struttura portante per il suo intero periodo di vita, pur non svolgendo un ruolo strutturale; Un inciso: nel caso dei tramezzi e degli impianti, non si procede con un calcolo analitico, bensì forfettario che tenga conto di una determinata incidenza a m² (nell0 specifico, 1kN/m² per i tramezzi e 0,5 kN/m² per gli impianti);

 

infine i carichi accidentali q_a, carichi dalla natura fortemente aleatoria quali vento, neve, sisma; ma anche i carichi d’esercizio legati alla funzione che svolgerà l’edificio (per questa esercitazione, sempre su vostro suggerimento, prenderemo in considerazione solamente i carichi d’esercizio regolati dalle NTC2008, ossia le Norme Tecniche per le Costruzioni – D.M. 14 Gennaio 2008);

 

Caliamoci però nello specifico della nostra esercitazione: prendo in analisi 1m² di solaio per ognuno dei tre tipi proposti (scelti in base all’abaco dei modelli UNI10355), distinguo gli elementi strutturali da quelli permanenti e calcolo il peso di ogni materiale contenuto nel m² moltiplicando il suo peso specifico (espresso in KN/m³) per la quantità di volume (espresso in m³/m²).

 

 

 

 

La qu, ossia la combinazione di carico per lo stato limite ultimo (il valore calcolato dal foglio Excel) non è dato dalla semplice somma di q_s, q_p e q_a, bensì dovranno essere tenuti da conto dei coefficienti moltiplicativi dei singoli carichi secondo la combinazione di carico seguente:

q_m²=γ_g1*q_s+ γ_g2*q_p + γ_g3*q_a.

I valori di γ sono riportati nella normativa in funzione dello stato limite ultimo:

 

 

Trovato il valore di carico che si riferisce ad 1m² di solaio (q_m²), per trovare ora il carico agente sulla trave bisognerà innanzitutto trovare la q_solaio agente sull’intero solaio di Area A (con A= area d’influenza = interasse*luce della trave), pari a: q_solaio=q_m²*A

A questo punto, per trovare il carico agente sulla trave basterà dividere il carico appena trovato per l’interasse i. Quindi:

 q_trave=q_solaio/luce= q_m²*i = qu

Determiniamo infine i Momenti Massimi agenti sulla trave. Basterà inserire la luce della trave ed il file Excel lo calcolerà tenendo da conto che ci troviamo dinnanzi l’ipotesi di una trave doppiamente appoggiata

M=(q_u*l²)/8

 

Legno

 

Acciaio

 

Calcestruzzo Armato

Passiamo quindi al dimensionamento della travi, partendo da quella in legno.

Innanzitutto, scegliamo il tipo di legno da utilizzare.

 

 

Scegliamo un GL 24c ed inseriamo nella tabella Excel la resistenza caratteristica a flessione f_m,k (dipendente non dall’essenza quanto dalla tecnologia – legno massiccio o lamellare – e dalla classe di resistenza).

La tensione di resistenza f_d sarà a sua volta pari a f_d = (k_mod*f_m,k)/γ_m

K_mod è un coefficiente diminutivo che tiene da conto l’effetto della durata del carico nonché le condizioni di umidità; per definirne il valore è necessario conoscere la durata del carico e la classe di servizio (il tutto è tabellato nelle normative).

Ipotizziamo un carico permanente ed una classe di servizio 2. Dal momento che il nostro è un legno lamellare, avremo un valore k_mod pari a 0,6.

 

 

 

Il coefficiente γ_m è invece un coefficiente parziale di sicurezza relativo al materiale pari – nel nostro caso - ad 1,45 (piuttosto alto se paragonato ai coefficienti di altri paesi).

Inserite quindi le informazioni geometriche, le caratteristiche del materiale e dopo aver determinato le tensioni di progetto, determino la sezione rettangolare scegliendo una base ed ottenendo un’altezza (in estrema sintesi, DATE la base, il Momento Massimo e la tensione di resistenza f_d, ricaviamo l’altezza della nostra sezione). Ipotizzando una base b=30cm

La nostra altezza minima sarà pari a:

h_min= (M_max/b)^0.5 * (6/f_d)^0.5 = 42,46 cm.

Ovviamente questa altezza andrà ingegnerizzata scegliendo un’altezza superiore al valore minimo compatibile con i profili esistenti sul mercato (arrivando – sempre nel nostro caso – ad un’altezza di 50cm).

Ora, riducendo i passaggi all’essenziale, spendiamo due righe su come si è arrivati a calcolare l’altezza minima della nostra trave, partendo dalla formula di Navier per la flessione

σ=(M_x/I_x)*y

Nel momento in cui devo verificare la mia trave, considero

σ_max=(M_max/I_x)*y_max =M_max/W

Con W modulo di resistenza a flessione che dipende dalle caratteristiche geometriche della sezione (in questo caso, essendo la trave rettangolare, y_max=h/2, il momento d’inerzia I_x =(bh³)/12 e conseguentemente W= (bh²)/6

Imponendo che il valore massimo di tensione (σ_max) sia pari al valore di progetto (f_d), posso determinare il valore minimo del modulo di resistenza a flessione della sezione (W_min) ed infine esplicitare il valore dell’altezza h, ottenendo la formula scritta poco sopra.

Dimensionamento trave in acciaio

Per il dimensionamento della sezione in acciaio, dobbiamo determinare il modulo di resistenza a flessione minimo da utilizzare affinché la tensione del materiale non superi la tensione di progetto. Sintetizzando: dati f_yd e M_max (calcolato precedentemente), ricaviamo W_x,min.

f_yd (f_d nel file Excel) è la tensione di progetto e si calcola a partire dalla tensione caratteristica di snervamento dell’acciaio prescelto e dividendola per un coefficiente di sicurezza γ_s pari a 1,05 (schiacciante il confronto con il coefficiente di sicurezza del legno).

F_yd = F_yk/ γ_s

Scegliamo un acciaio Fe 430/S275, con una tensione di snervamento caratteristica di 275 MPa. Inserendo il valore di f_yk, il file Excel mi calcola direttamente il W_x,min.

W_x,min = M_max/f_yd

Anche qui, il modulo di resistenza a flessione minimo lo abbiamo ricavato partendo dalla formula di Navier per la flessione (vedi quanto scritto per il dimensionamento della trave lignea).

Essendo stato effettuato il calcolo considerando lo stato limite ultimo (fd = σ_max), W_x,min è il valore minimo(affermazione leggermente tautologica, d’accordo) che posso scegliere per il dimensionamento. Dovrò, come sempre, ingegnerizzare i risultati ottenuti. Avendo ottenuto quindi un W_x,min = 485,51 cm3, sceglierò una IPE300 con W_x = 557,1 cm3.

Trave in calcestruzzo armato con sezione rettangolare

Infine, la trave in calcestruzzo armato. In questo caso i dati del progetto sono i valori delle tensioni di progetto del cls (f_cd) e dell’acciaio (f_yd), nonché la base, il Momento massimo e δ (la distanza tra il baricentro dell’armatura inferiore ed il filo del cls teso, che imponiamo uguale a 5cm).

Iniziamo scegliendo il tipo di acciaio ed il tipo di calcestruzzo che utilizzeremo, determinando prima f_yk ed f_ck (le resistenze caratteristiche dell’acciaio e del calcestruzzo), poi f_cd e f_yd (le tensioni di progetto del calcestruzzo e dell’acciaio)

f_yd = f_yk/ γ_s             f_cd = α_cc(f_ck/ γ_c)

γ_s  è il coefficiente parziale di sicurezza relativo all’acciaio (pari a 1,15), α_cc è il coefficiente riduttivo per le resistenze di lunga durata (0,85) e γ_c il coefficiente parziale di sicurezza relativo al cls, pari a 1,5.

Scegliamo un acciaio B450A (con f_yk = 450 MPa) ed un calcestruzzo ordinario C 25/30 (f_ck = 30 MPa)

Definendo quindi la base della nostra sezione (30cm) e noti i valori delle tensioni di progetto, determiniamo h_u (l’altezza utile della sezione, pari all’altezza totale meno δ), da cui poi otterremo appunto una H_min (altezza minima della sezione).

H_min = h_u + δ

h_u = r(M_max/b)^0.5    con r = (2/[f_cd*(1-β/3)* β])^0.5      e     β= f_cd/(f_cd+f_yd/n)

L’altezza minima andrà poi ingegnerizzata in eccesso. Nel nostro caso quindi, ottenendo una h_u = 33,41 cm avremo una H_min= 38,41cm, che ingegnerizziamo prendendo un’altezza H = 45cm.

 

A questo punto, a differenza dei due casi precedenti con la trave in legno o in acciaio, dovremo fare nuovamente i calcoli aggiungendo al carico totale qu il peso proprio della trave (il peso specifico del cls armato è pari a 25kN/m³, che dovrà esser moltiplicato per il volume), moltiplicato per un fattore di sicurezza pari a 1,3. Se l’altezza minima risultante sarà ancora minore dell’altezza ingegnerizzata da noi scelta, la sezione risulterà verificata anche una volta aggiunto il peso proprio della trave (si veda quindi che, qualora fosse stata scelta un’altezza pari a 40cm – comunque maggiore della h_u,min, la sezione non sarebbe stata verificata una volta aggiunto il peso proprio; si è dovuto quindi ricorrere ad una H maggiore, pari appunto a 45cm).

L’esercitazione è finita, vorrei spendere solo alcune righe per spiegare in maniera molto sintetica (proponendo solo alcuni passaggi i concetti fondamentali alla base delle formule utilizzate per calcolare l’altezza utile minima della sezione in calcestruzzo.

Le ipotesi di progetto sono la conservazione delle sezioni piane e che entrambi i materiali attingano contemporaneamente la tensione di progetto. Queste ipotesi ci permettono di sfruttare la legge di Hooke (σ = E*ε) ed impostare una proporzione tra allungamenti, deformazioni e tensioni.

Una delle caratteristiche fondamentali del calcestruzzo armato è la non omogeneità del materiale (si parla di tre materiali: acciaio, calcestruzzo compresso e calcestruzzo teso). Risulta necessario operare un procedimento di omogeneizzazione tra le tensioni presenti nell’acciaio e quelle presenti nel calcestruzzo (mettendole in rapporto tra di loro), rapporto che viene infine ridotto a quello tra i rispettivi moduli elastici (E_f/E_c), pari a 10 e portato a 15, in quanto il modulo elastico del calcestruzzo diminuisce con il passare del tempo (n=15).

Potremo quindi scrivere σf =n σc

Avremo quindi un diagramma delle sollecitazioni di questo genere:

Ora, per progettare la sezione, posto σ_f =  f_yd  e σ_c = f_cd , dobbiamo ricavare la distanza X_c tra il lembo superiore compresso e l’asse neutro (non coincidente con quello geometrico). Per far questo, impostiamo un’eguaglianza tra triangolo (dividendo f_yd per n).

Noto X_c (che esprimiamo in funzione di h_u), sappiamo che il momento flettente esterno è dato da una coppia interna che vede la compressione sul calcestruzzo e la trazione sull’acciaio. Ponendo il centro di rotazione in T, calcoliamo il Momento M=C*b* (con b*=h_u – X_c/3 e C=(f_cd*b*X_c)/2), possiamo infine esplicitare il valore minimo dell’altezza utile h_u.

 

 

 

 

Ho deciso di riproporre la parte terminale – verso terra – di quella che ritengo essere un’interessante struttura reticolare spaziale disegnata da Burckhardt + Partner, l’MFO Park a Zurigo.

Parto scegliendo le unità di misura con le quali voglio lavorare (kilo newton, metri, gradi centigradi) ed impostando una griglia che mi servirà come base per la struttura.

Disegno quindi il “modulo base” che ripeto poi sia lungo l’asse x che lungo l’asse y (stravolgendo in parte il progetto di Burckhardt nel raddoppiare la campata; questo ai fini dell’esercitazione, così da applicare carichi diversi che tengano conto della diversa area d’influenza).

Definisco la sezione che voglio utilizzare (rinominata Tubolare_Esercitazione1) e la assegno alle aste della mia struttura. Rilascio i momenti su tutti nodi (quindi all’inizio ed alla fine di ogni asta), rendendoli cerniere interne.

Passo ad assegnare i vincoli esterni (8 cerniere) ed applico i carichi sui nodi: la forza concentrata F per quelli interni, la forza concentrata F/2 sopra i nodi del perimetro esterno (questo perché, come già accennato prima, i carichi agiscono su una superficie attorno al nodo che corrisponde alla metà della superficie sulla quale agiscono i carichi posti sui nodi interni).

Ora, l’analisi. Il programma permette di visionare la deformata, i diagrammi dello sforzo normale (il colore rosso sta a rappresentare un valore di compressione, quello blu di trazione) e quelli del momento. Questi ultimi – come da programma – risultano nulli. Alcune aste (quelle diagonali lungo il piano x-y ad altezza 2m) non presentano sforzo assiale (nel caso di carico concentrato); sono comunque necessarie come controventi, per far sì che la struttura sia reticolare e non labile.

Passiamo quindi al dimensionamento. Esportiamo da SAP su Excel una tabella che mostri ogni valore dello sforzo normale lungo le aste. La tabella può essere fortemente ridotta: il programma riporta infatti i valori dello sforzo normale su una singola asta quantomeno tre volte; essendo nel nostro caso lo sforzo costante lungo la stessa asta, possiamo mantenere un solo valore. Nel caso specifico, mantengo quello calcolato all’estremità dell’asta, così da sapere anche la lunghezza totale dell’asta alla quale è associato lo sforzo Normale (essendoci diverse aste diagonali, controllo su SAP la lunghezza delle aste). Divido quindi la tabella in due sottogruppi: aste compresse (in rosso) ed aste tese (in nero).

Finalmente il dimensionamento vero e proprio. I procedimenti saranno diversi a seconda che si parli di aste tese o di aste compresse. Nel primo caso, basterà confrontarsi con la resistenza del materiale; abbiamo quindi un solo fenomeno di crisi di cui tener conto: che la tensione nel materiale non raggiunga la tensione di progetto.

Nel caso delle aste compresse i fenomeni di crisi sono invece due. Uno avente sempre a che fare con la resistenza del materiale (come già detto per l’asta tesa), l’altro con l’instabilità euleriana (fenomeno particolarmente insidioso dal momento che le equazioni in gioco sono fortemente non lineari). Le incognite sono in questo caso due: l’area minima (necessaria per la rottura) ed il momento d’inerzia (necessario per l’instabilità).

Ma vediamo il ragionamento applicato al caso specifico, cominciando dalle aste tese.

Inserisco il valore dello Sforzo Normale di Trazione nella tabella Excel, scelgo un acciaio (S235) con i relativi valori di f_yk (coefficiente di snervamento, in questo caso 275 MPa) e γ_m (coefficiente di sicurezza pari a 1,05). Noti questi valori, posso trovarmi la tensione di progetto f_yd (uguale al rapporto tra il coefficiente di snervamento f_yk ed il coefficiente di sicurezza γ_m) e l’area minima di progetto A_min (uguale al rapporto tra il valore dello sforzo Normale e la tensione di progetto f_yd).

Con le tabelle dei profilati metallici tubolari sotto mano ed il valore ora noto di A_min (che va ingegnerizzato, ossia arrotondato al valore del profilo standard disponibile immediatamente superiore al valore trovato), scelgo finalmente i diversi profilati. Nel nostro caso, visti i valori irrisori di sforzo di trazione a cui sono sottoposte le aste, abbiamo dei valori di A_min che non superano 1,9cm²; possiamo quindi scegliere un unico profilato 33,7mm x 2,6mm (d x s) per tutte le aste tese.  

Infine, le aste compresse. Assumo i valori di f_yk e γ_m uguali a quelli utilizzati per le aste tese. Nell’inserire i valori dello sforzo Normale di compressione nelle tabelle, ne facciamo il modulo, così da renderli positivi. Nel caso delle aste compresse, come accennato prima, bisogna tener da conto anche il fenomeno dell’instabilità. Il valore di N non deve superare N_E, il carico critico euleriano , pari al prodotto

N_E = (π²*E*I_min)/(l_o²).

E rappresenta il modulo d’elasticità normale del materiale, pari a 210000 MPa, I_min il momento d’inerzia minimo della sezione, ossia l’asse lungo cui è più facile che il pilastro “svirgoli”, l_o la lunghezza minima d’inflessione, pari al prodotto tra l e β  (rispettivamente la lunghezza dell’asta – motivo per cui nella tabella Excel abbiamo mantenuto i valori dello sforzo Normale calcolati all’estremità dell’asta! – ed un coefficiente beta dipendente dai vincoli, nel nostro caso pari ad 1). E’ evidente che nel progetto di un’asta compressa ricerco un elevato valore di I_min ed un ridotto valore di l_o²(l_o*l_o). Introducendo il valore di ρ_min (il raggio d’inerzia minimo della sezione, una sorta di ellisse che rappresenta l’andamento dell’inerzia lungo la sezione), posso riscrivere I_min come il prodotto tra l’Area e ρ_min² ed introdurre la snellezza λ pari al rapporto tra l_o e ρ_min e riscrivere quindi l’equazione N_E tenendo conto di quest’ultimo valore. Senza adesso entrare eccessivamente nella discussione teorica ed allontanandoci così dal fine dell’esercitazione, ma anzi tornando al dimensionamento della travatura reticolare, risulta comunque evidente da questi pochi accenni come a fianco al valore dell’Area minima – nel caso dell’asta sottoposta a compressione – altrettanto fondamentale sia il valore del momento d’inerzia minimo.

Nel nostro caso, i valori di A_min non superano 3,8cm². I valori girano attorno a 2,1cm², 2,7cm², 3,5cm² e 3,8cm²…dovessimo tener da conto il solo valore dell’area minima, potremmo ipotizzare una struttura estremamente “performante” scegliendo tre profilati diversi: 33,7mm x 2,9mm, 42,4mm x 2,9mm e 42,4mm x 3,2mm.

Dobbiamo però tener da conto anche il momento d’inerzia. L’I_min della struttura analizzata variano dai 10cm⁴ ai 35cm⁴, passando per 14cm⁴, 19cm⁴, 22cm⁴, e 27cm⁴. Sceglieremo quindi dei profilati ben più grandi di quanto non avremmo fatto tenendo conto della sola area min. Giocando sempre al gioco utopistico della “struttura performante” portata all’estremo, sceglieremo quattro tipi di profilati: 48,3mm x 3,2mm, 60,3mm x 2,9mm, 60,3mm x 3,2mm e 76,1mm x 2,6mm.

Abbiamo così dimensionato la struttura reticolare spaziale. Potrei riassegnare le sezioni su SAP e mandare nuovamente l'analisi, ma sarebbe (quantomeno ai fini dell'esercitazione) un qualcosa di eccessivamente scrupoloso. Questo perchè, essendo le aste d'acciaio, non è necessario mandare novamente l'analisi tenendo da conto il peso della struttura (o meglio, essendo il peso piccolo rispetto ai carichi, lo si tiene indirettamente da conto nel momento dell'ingegnerizzazione immediatamente precedente la scelta del profilato).