Esercitazione 3_Verifica a deformabilità di tre travi a sbalzo (mensole) in legno, acciaio e calcestruzzo armato

Pur presentando una carpenteria differente rispetto a quella proposta nella precedente esercitazione (mantenere le stesse dimensioni per verificare le diverse esigenze in termini di geometria della sezione rispetto alle due diverse verifiche sarebbe stato interessante qualora la struttura isostatica proposta fosse stata la stessa; in questo caso, tuttavia, ci troviamo di fronte ad una mensola, non più di fronte ad una trave appoggiata-appoggiata), riproporrò gli stessi solai (in legno, acciaio e calcestruzzo armato) e gli stessi materiali (legno Gl 24c, acciaio Fe 430/S275, calcestruzzo C 25/30 con barre d’acciaio B450A) riprendendo quindi alcuni dati e modificandone altri. 

 

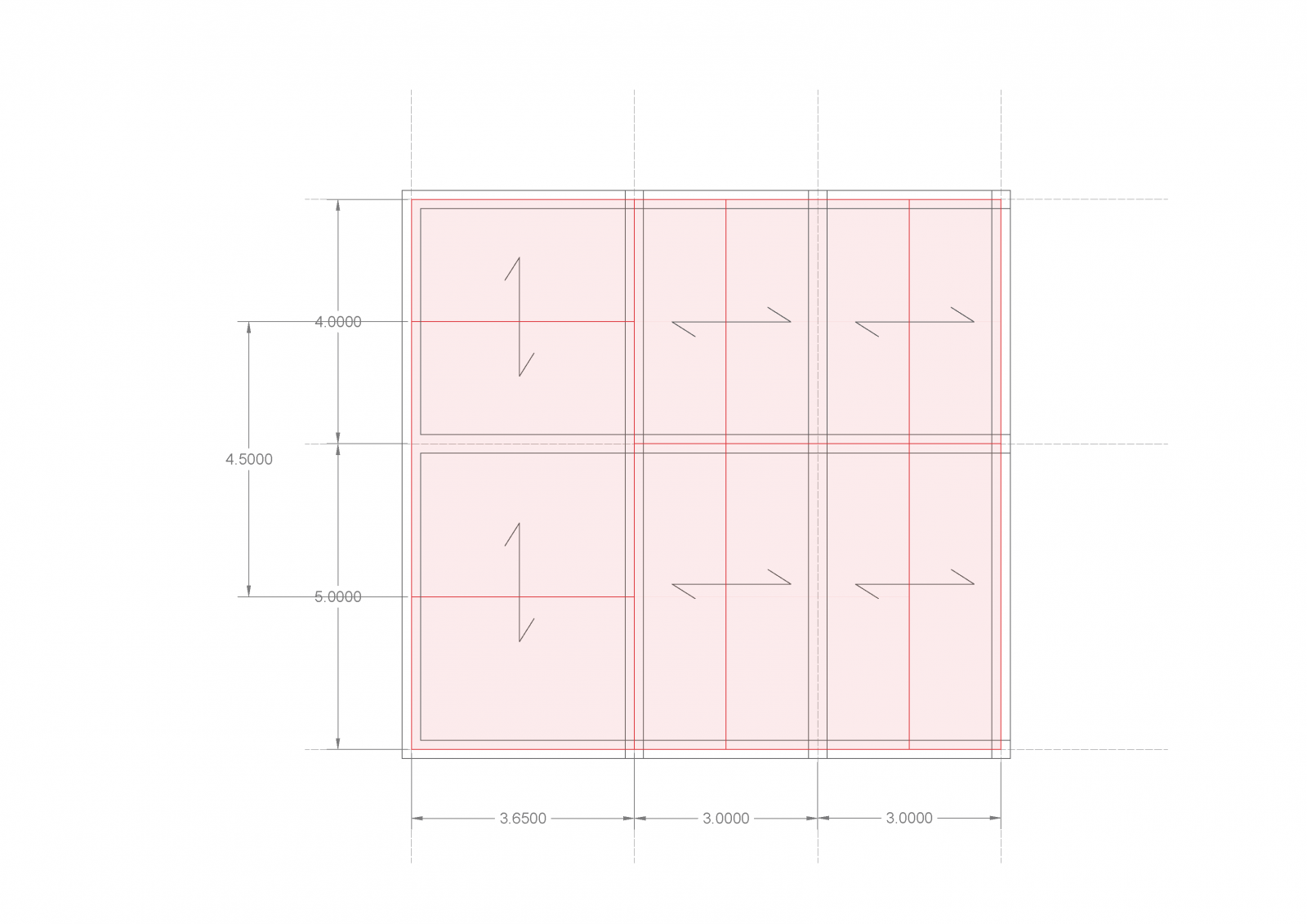
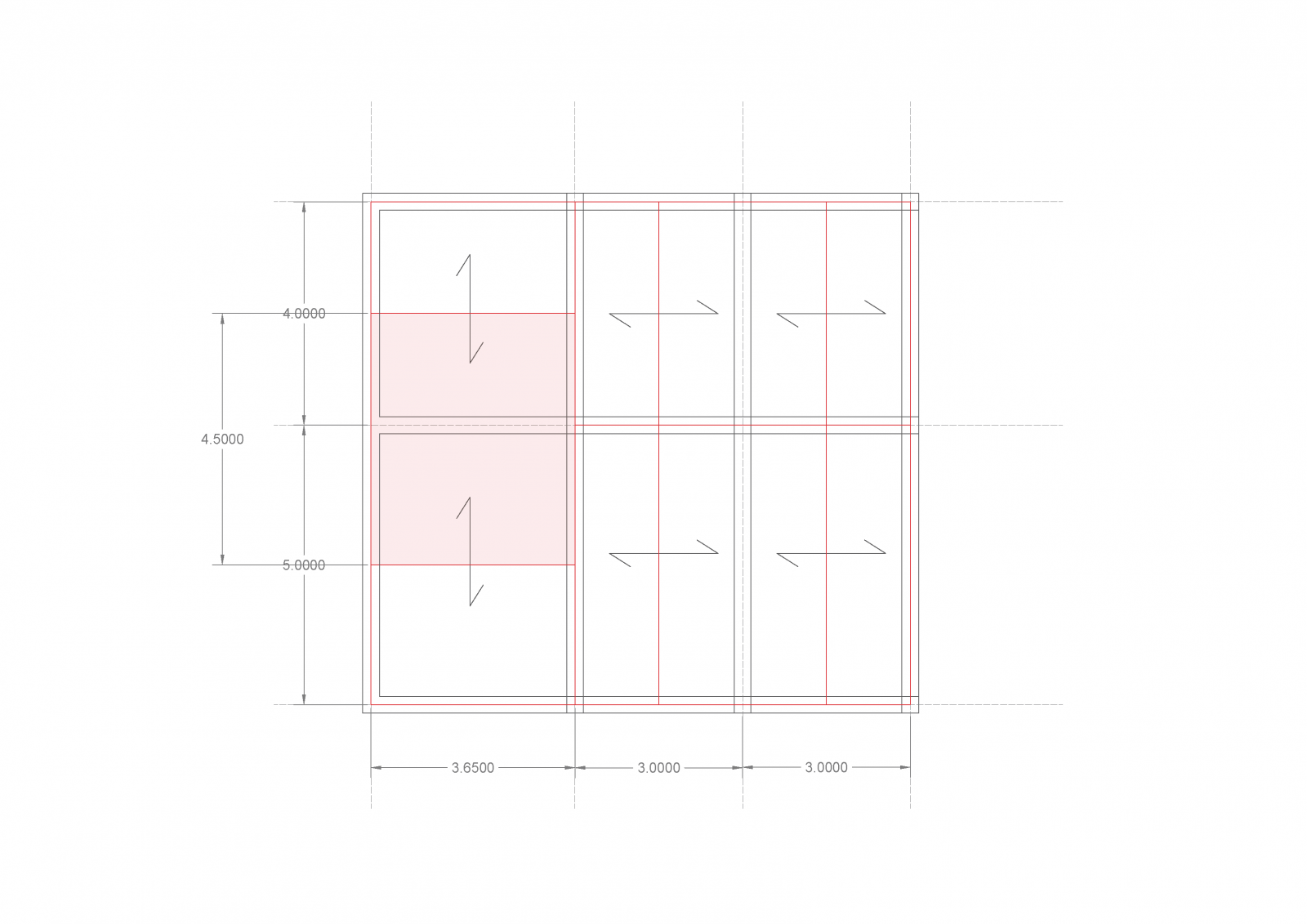
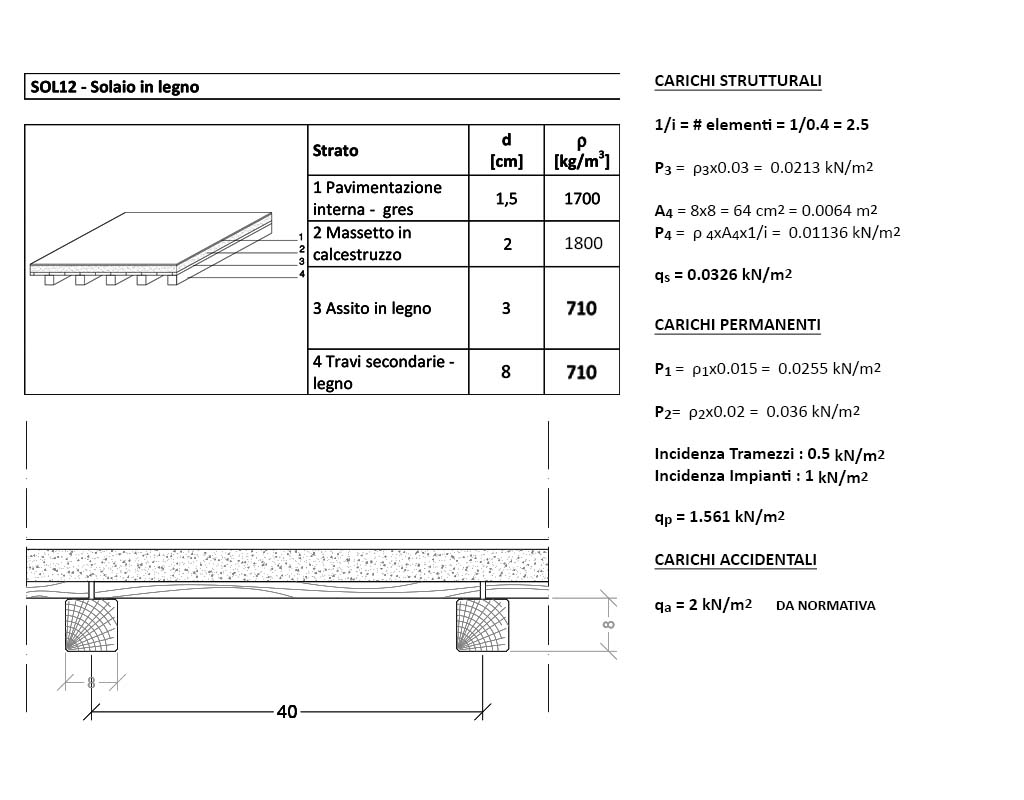
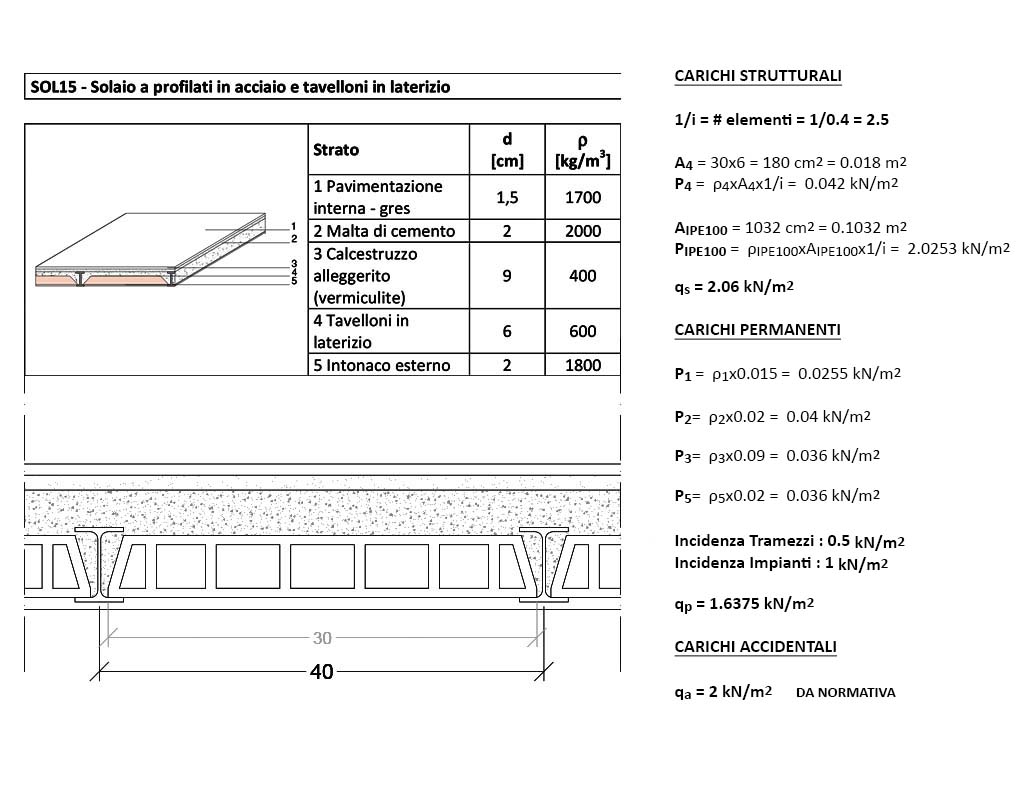
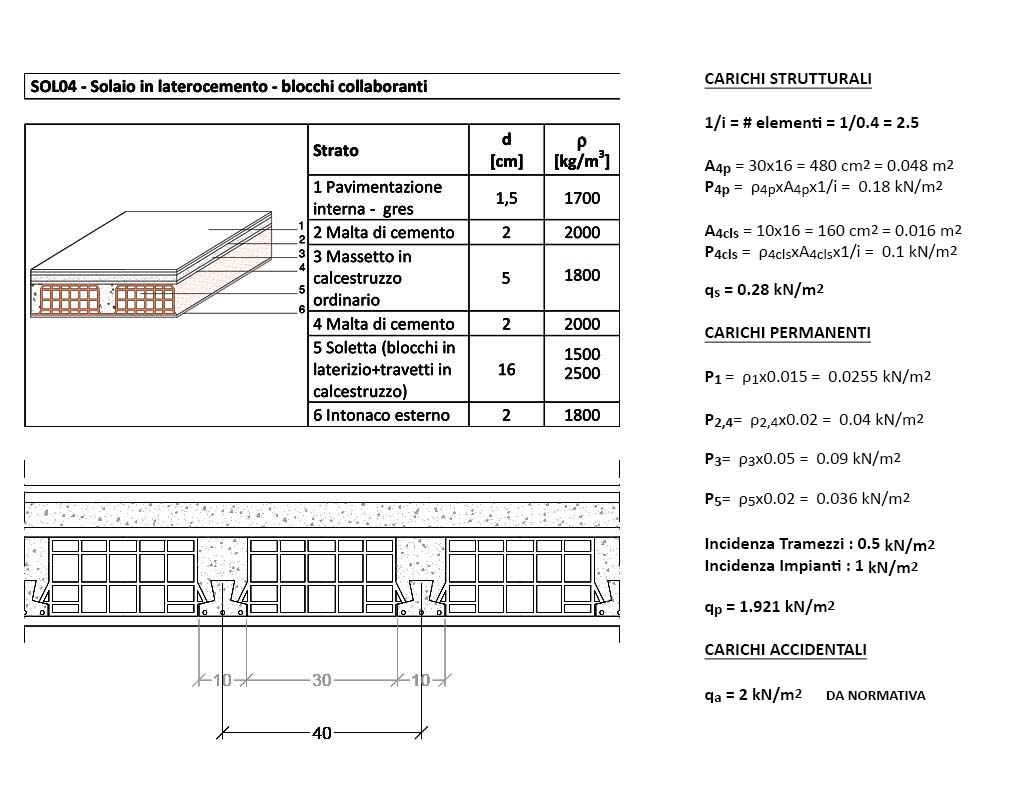
Lo scopo della terza esercitazione è quello di effettuare su queste tre mensole, da non confondere con aggetti, la verifica a deformabilità, controllando l’abbassamento minimo dell’elemento strutturale in rapporto alla sua luce. A proposito di mensole ed aggetti, cercherò di dare una definizione empirica della differenza tre le due: la geometria delle prime “termina” nel momento in cui entra in contatto con la parete o il pilastro che la sostiene (mettendo gli occhiali della cinematica, diremmo dell’incastro); i secondi, invece, continuano. Detto altrimenti, mentre le mensole sono corpi “interamente” a sbalzo, gli aggetti ne presentano solo una parte.

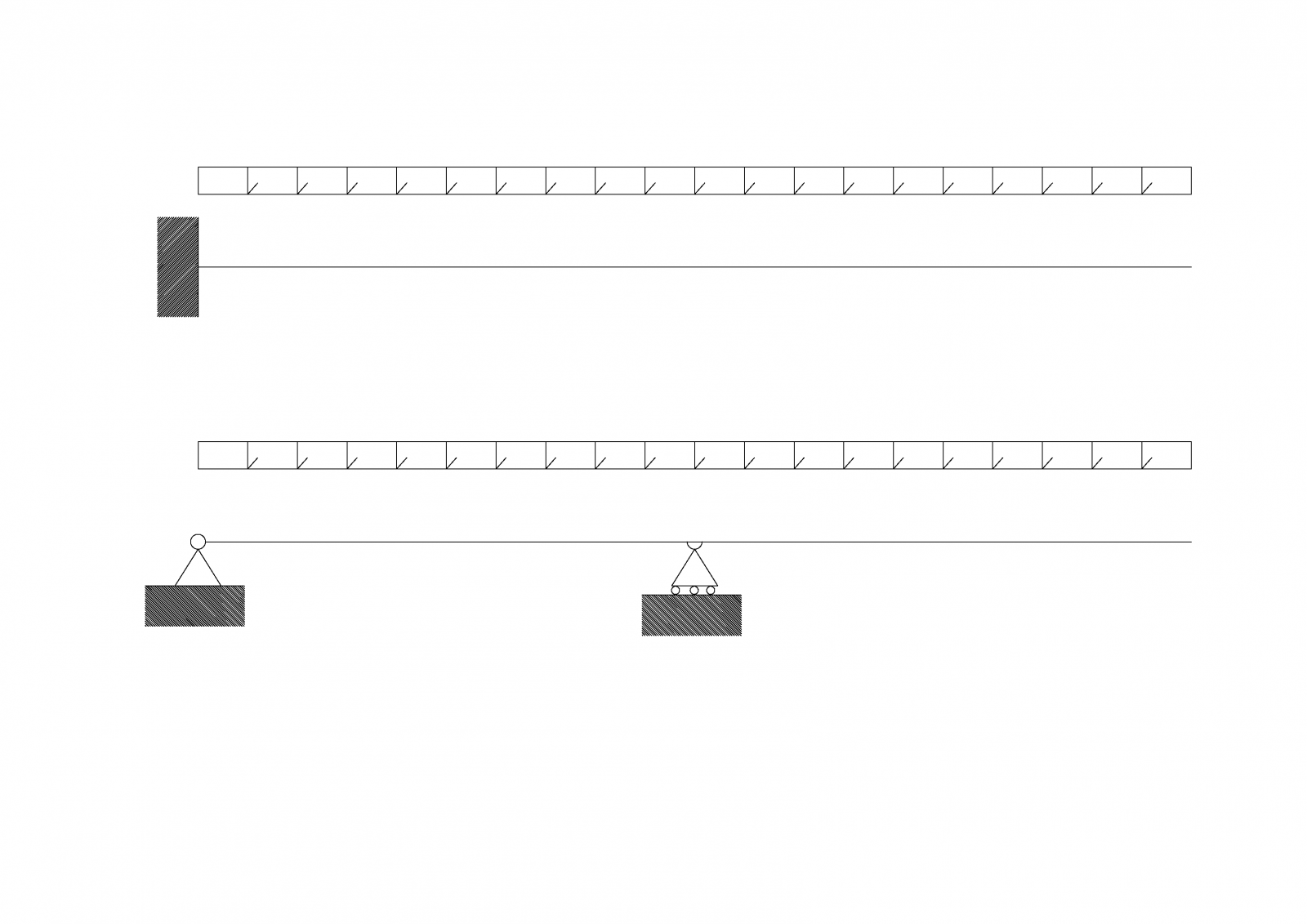
Il procedimento è analogo (seppur con alcune differenze che vedremo) per tutte e tre le tecnologie, e da effettuarsi allo Stato Limite d’Esercizio (SLE), differentemente da quanto avvenuto invece per il dimensionamento delle travi nella precedente esercitazione, che ha avuto luogo allo Stato Limite Ultimo (SLU). La motivazione è chiara: il tipo di verifica che ci interessa - in questo caso - non è finalizzata ad esser sicuri o meno che la struttura non si “rompa”; ci si pone un gradino sotto, controllando che non vi siano spostamenti che possano limitare l’uso della costruzione, la sua efficienza ed il suo aspetto. Torniamo quindi con un concetto già accennato nella prima esercitazione a proposito delle due fondamentali operazioni di verifica da applicare sulle strutture: le prime di carattere fondamentale (la verifica a rottura allo SLU), che pongono in gioco questioni vitali riguardo la rottura della struttura e la salvaguardia stessa della vita umana; le altre inerenti al benessere (la verifica a deformabilità allo SLU).

Ipotizziamo in tutti e tre i casi di trovarci dinnanzi ad una mensola di lunghezza l e caricata con un carico uniformemente distribuito pari a q_u. Evidentemente, il momento massimo – in corrispondenza della sezione d’incastro – varrà

M_max=(q_u*l²)/2

L’importanza nel sottolineare il tipo di carico (distribuito o concentrato) nonché – nel caso di carico distribuito – il tipo di distribuzione (uniforme o non) è cruciale: questo condiziona il momento massimo che a sua volta influenza lo spostamento minimo (insieme ad altri fattori che vedremo in seguito: il Modulo Elastico ed il Momento d’Inerzia).

Entriamo quindi nel vivo della terza esercitazione.

Nell’aprire il file Excel ci troviamo di fronte – nella parte inziale – ad un qualcosa di già visto nell’esercitazione numero due (eccezion fatta per il valore del momento massimo nella sezione maggiormente sollecitata; del resto stavamo prendendo in considerazione una trave doppiamente appoggiata). Iniziamo quindi con il ricavarci, con un procedimento analogo a quello già applicato in precedenza (per una descrizione dettagliata di tutti i passaggi riferirsi quindi alla suddetta esercitazione), la geometria delle nostre mensole, attraverso il calcolo dell’altezza minima (nel caso del legno e del calcestruzzo armato) oppure del modulo di resistenza a flessione minimo (nel caso dell’acciaio).

Per un interasse di 4,5m ed una luce di 3m, con le caratteristiche dei materiali precedentemente descritti, otterremo una sezione lignea di 30x60, una IPE300 ed una sezione in calcestruzzo armato 30x50 (ovviamente dopo le necessarie ingegnerizzazioni). 

Legno

Acciaio

Calcestruzzo armato

 

Quindi, dopo aver dimensionato le sezioni allo SLU, possiamo verificarne la deformabilità allo SLE. Ed è proprio poiché questo tipo di verifica (per motivazioni introdotte prima) viene fatto allo stato limite d’esercizio che i carichi incidenti sulla struttura vengono ricombinati seguendo la combinazione frequente, generalmente impiegata per gli stati limite di esercizio reversibili:

q_e= (G1 + G2 + ψ_11*Q₁) _* i con

G1 = rappresenta il valore caratteristico del peso proprio di tutti gli elementi strutturali (sostanzialmente q_s);

G2= il valore caratteristico del peso proprio di tutti gli elementi non strutturali (q_p);

ψ₁₁ = coefficiente che definisce il valore frequente dell’azione variabile Q1, assimilabile al valore medio della distribuzione temporale dell’intensità (pari nel nostro caso a 0,5);

 

Q₁₌ il valore caratteristico dell’azione variabile (q_a);

i = interasse

Ma non si riduce a questo la differenza rispetto alla verifica allo SLU. Ad esempio: nel caso del legno (il materiale più leggero fra i tre) il peso proprio della trave viene trascurato, come avviene anche nel caso di verifica a rottura allo Stato Limite Ultimo. Tuttavia, non è così non solo per il calcestruzzo armato, ma anche per l’acciaio; si dovrà quindi inserire nel foglio di calcolo anche il suo di peso, in kN/m (la nostra IPE300 pesa 42,2 kg/m, ossia 0,42 kN/m circa). Per questi ultimi due materiali quindi, il peso proprio verrà preso in considerazione per ricavare il carico totale q_e.

Nel nostro caso specifico, i pesi delle strutture che bisogna aggiungere per trovare il carico totale q_e sono:

3,75 kN/m per il calcestruzzo;

0,42 kN/m per l’acciaio;

Infine, il calcolo dello spostamento. Come già accennato, abbiamo bisogno di altre due informazioni oltre al valore del momento massimo: una relativa al materiale di cui è composta la mensola (ossia il suo modulo di elasticità, brutalmente sintetizzabile come il rapporto tra la tensione e la deformazione), l’altra relativa alla sua geometria (il momento d’inerzia I_x).

Questi valori sono rispettivamente:

E_legno =   11600 N/mm²  è il modulo elastico medio parallelo (da utilizzare nel caso di verifiche allo stato limite d’esercizio), non il modulo elastico caratteristico (da utilizzare per verifiche allo stato limite ultimo;

E_acciaio = 200000 N/mm²

E_calcestruzzo = 25000 N/mm²

I_x,legno = 540000 cm⁴

I_{x, acciaio} = 8356 cm⁴

I_{x, calcestruzzo} = 312500 cm⁴

Noti questi valori, possiamo calcolarci lo spostamento (abbassamento) massimo di una mensola sottoposta a carico uniformemente distribuito:

 v_max= - (q_e*l⁴)/8_*E_*I_x

Nel nostro caso, gli spostamenti saranno pari rispettivamente a:

v_max,legno= 0,41 cm

v_max,acciaio= 0,898 cm

v_{max,calcestruzzo armato}= 0,24 cm

L’esercitazione si conclude verificando che il rapporto tra la luce della trave ed il suo spostamento massimo sia maggiore di 250, come imposto dalla normativa di base al tipo di elemento strutturale considerato: l/vmax dev’essere minore od uguale a 250. Nel nostro caso, i rapporti sono tutti e tre verificati.

l/ v_max,legno = 882,97

l/ v_max,acciaio = 334,022

l/ v_{max,calcestruzzo armato} = 1275, 38

Legno

Acciaio

Calcestruzzo armato

 

Vorrei adesso spendere alcune righe sul come siamo arrivati a formulare lo spostamento massimo di una mensola con carico uniformemente distribuito. Per ricavare lo spostamento di questo schema isostatico noto prendiamo come base la trave di Bernoulli descritta da tre gruppi di equazioni:

quelle di Bilancio (siamo in campo statico)

dN/ds + q1 = 0

dT/ds + q2 = 0

dM/ds + T + μ = 0

quelle di Congruenza (siamo in campo cinematico)

ε_(s) = dv/ds

γ_(s) = dv/ds – ϕ_(s)

χ_(s) = d ϕ/ds

quelle del legame costitutivo (che fanno da trait d’union tra il campo statico e quello cinematico)

N_(s) = E_*A_*ε(s)

M_(s) = E_*I_* χ(s)

Partiamo quindi operando un taglio virtuale di Cauchy sulla nostra mensola; l’equazione in funzione di s che descriverà l’andamento del momento lungo la mensola sarà:

M_(s)=-(q_*l²)/2 + q_*l_*s – (q_*s²)/2

A partire da questa otterremo lo spostamento verticale in funzione di s integrando l’equazione tre volte, passando per la curvatura e la rotazione:

χ_(s) = -(q_*l²)/2_*E_*I + (q_*l_*s)/E_*I – (q_*s²)/2_*E_*I

ϕ_(s)= -(q_*l²_*s)/2_*E_*I + (q_*l_*s²)/2_*E_*I – (q_*s³)/6_*E_*I +c₁

v_(s)= -(q_*l²_*s²)/4_*E_*I + (q_*l_*s³)/6_*E_*I – (q_*s³)/24_*E_*I +c_1*s + c₂

Il valore di v ci è noto a meno di due costanti, che otteniamo analizzando due condizioni al bordo. Essendoci un incastro come vincolo, avremo che:

ϕ₍₀₎ = 0

v₍₀₎ = 0

Conseguentemente, c₁ = 0 e c₂ = 0, mentre v_(s=l) = -(q_*l⁴)/8_*E_*I, con il segno meno in quanto abbassamento. c.v.d.

Terminiamo constatando che, cambiando tipologia di carico (passando quindi da un distribuito uniforme ad un concentrato al centro e nell’estremo sena vincoli), non necessariamente cambierà il valore del momento massimo nella sezione più sollecitata (nel primo caso rimarrà sempre M_max = (q_*l²)/2, mentre nel secondo varia: M_max = q_*l²), mentre varia lo spostamento massimo:

v_max = -(7_*q_*l⁴)/78_*E_*I            nel caso del carico concentrato al centro

 

v_max = -(q_*l⁴)/24_*E_*I                nel caso del carico concentrato nell’estremo libero

Entrambi i valori si ottengono con procedimento analogo a quello descritto sopra, partendo dall’equazione del momento lungo la mensola in funzione di s ed integrandola tre volte (dividendo i due campi 0 < s < l/2 e l/2 < s < l nel caso di carico concentrato al centro).

Verifichiamolo velocemente creando due nuovi file Excel.

Nel primo caso ipotizziamo un carico ql concentrato e centrato. La formula del M_max non varia, mentre varia quella dello spostamento. La verifica va comunque a buon fine.

Legno

Acciaio

Calcestruzzo Armato

Nel secondo ipotizziamo invece un carico ql concentrato nell’estremo non vincolato. Cambierà tanto la formula dello spostamento, quanto quella del momento massimo (nel caso del calcestruzzo, bisogna ricordarsi di cambiarla due volte, la seconda nel momento in cui viene aggiunto il peso proprio e verificata nuovamente la fattibilità della geometria scelta. Anche in questo caso, la verifica va comunque a buon fine.

Legno

Acciaio

Calcestruzzo armato