Esercitazione 2_Dimensionamento di una trave inflessa in legno, acciaio e cemento armato

L'esercitazione richiede il dimensionamento di una trave secondo i tre piu comuni materiali da costruzione:legno,acciaio e cemento armato. Per questo, come prima cosa prendo in considerazione la pianta di carpenteria di un generico edificio e ne individuo la trave maggiormente sollecitata tenendo conto della sua luce, area di influenza e dell'interasse.

Per ricavare il carico totale a metro lineare agente sulla trave (q_u) partiamo da una formula che utilizza 3 fattori - carico strutturale qs (peso degli elementi portanti); carico permanente q_p (elementi che gravano sulla struttura portante per il suo intero periodo di vita e che non svolgono un ruolo strutturale) carico accidentale q_a (carichi di esercizio e carichi variabili nel tempo) - sommati fra loro tenendo conto di due precisazioni:

1)

 coefficienti moltiplicativi dei singoli carichi, secondo la seguente formula:

q_tot [kN/m²]  = Y_G1q_s + YG2q_p  + Y_Q1q_a

 

COEFFICIENTI MOLTIPLICATIVI IN FUNZIONE DELLO STATO LIMITE ULTIMO CONSIDERATO (Nel caso dell'esercitazione si considera  lo s.l.ultimo relativo alla verifica della resistenza della struttura)

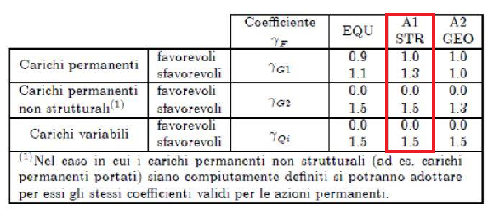
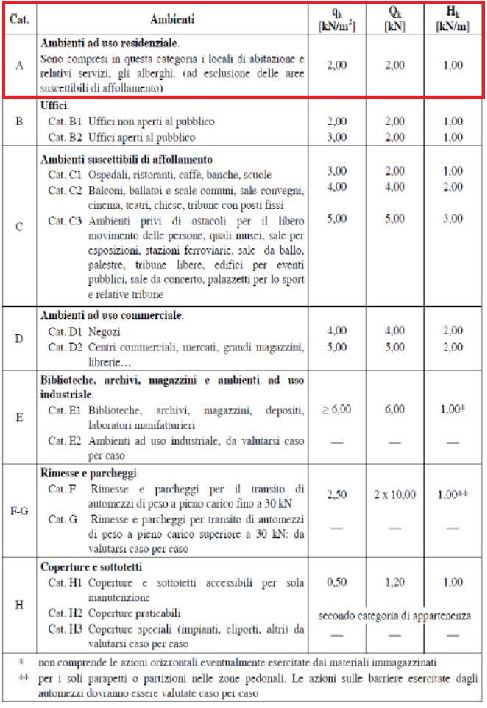
CARICHI ACCIDENTALI PER CATEGORIA DI EDIFICI (si prende in considerazione il valore dei carichi accidentali per edifici ad uso residenziale)

2)

Il fatto che la formula precedente è relativa al carico previsto dalla normativa per un metro quadro (q_{solaio[kN/m²]} ) di solaio, mentre quello che si vuole ricercare è il carico totale agente sulla trave (lineare, espresso in kN/m). Quindi, conoscendo l'area di influenza (A_{rea di influenza} = i x l) utilizziamo la seguente formula:

                                                q_totale  =  q_{solaio[kN/m²]} x A_{rea di influenza}  =  q_{solaio[kN/m²]} x  (i x l)

e otteniamo il carico totale agente sulla trave:

                                                                  q_trave[kN/m]  =  q_totale / l  = q_{solaio[kN/m²]} x  i 

 

A questo punto, conoscendo q_u =  q_trave[kN/m], si può calcolare il Momento massimo agente sulla trave. Nel caso di questa esercitazione il vincolo che il pilastro esercita sulle travi è ritenuto di appoggio semplice, dunque M_(max) si trova nella mezzeria della trave e vale: 

                                                                        M_(max) = q_ul / 8

 

I dati sopra ricavati sono necessari ai fini del dimensionamento della trave secondo i tre materiali che vengono presi inconsiderazione in questa esercitazione: acciaio, legno e cemento armato.

  

TRAVE IN LEGNO

Prendo in analisi un metro quadro (m²) di un solaio in legno rappresentato in sezione, e definisco i diversi tipi di carico agenti sulla struttura individuandone i pesi specifici:

 

SEZIONE SOLAIO IN LEGNO                                                                           

 

 

q_s = 0.42 kN/m2                      CARICO STRUTTURALE 

q_p = 2.83 kN/m2                      CARICO PERMAMENTE        

q_a = 2     kN/m²                       CARICO ACCIDENTALE             

                           

A questo punto inserisco i valori nella tabella Excel relativa al dimensionamento di una trave e ottengo il valore di q_u =  q_trave[kN/m] e M_max.

Per dimensionare la trave scelgo un legno lamellare incollato omogeneo (GL28h) che ha una resistenza caratteristica pari a f_mk = 28  ed un coefficiente di sicurezza pari a Y_m = 1.45 come riportato in tabella.

Tengo anche conto del k_mod, il  coefficiente diminutivo dei valori di resistenza del materiale, che tiene in conto l’effetto della durata del carico e delle condizioni di umidità in cui la struttura si troverà ad operare ed è fornito dalla normativa.Per definirne il valore, è necessario conoscere la durata del carico e la classe di servizio. 

Considerando una durata del carico permanente (>10 anni) ed una classe di servizio 2 si ha un  k_mod =0.6

Inserisco i dati ricavati nella tabella excel ed il programma mi fornisce il valore della tensione di progetto f_d secondo la seguente formula:

                                                       f_d = k_mod f_m,k / y_m

 

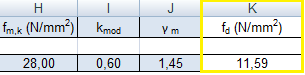
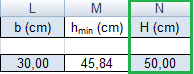
A questo punto, ipotizzando una base b = 30cm, il foglio di calcolo, secondo la formula h_min =(M_max/b)^½ ( 6/f_d )^½ ci fornisce l'altezza minima della nostra trave. Operando un ingegnerizzazione, scelgo un'altezza per la trave di 50 cm.

 

TRAVE IN ACCIAIO

Per quanto riguarda l'acciaio, il procedimento è analogo a quello del legno fino al calcolo del Moment massimo.

SEZIONE SOLAIO IN ACCIAIO

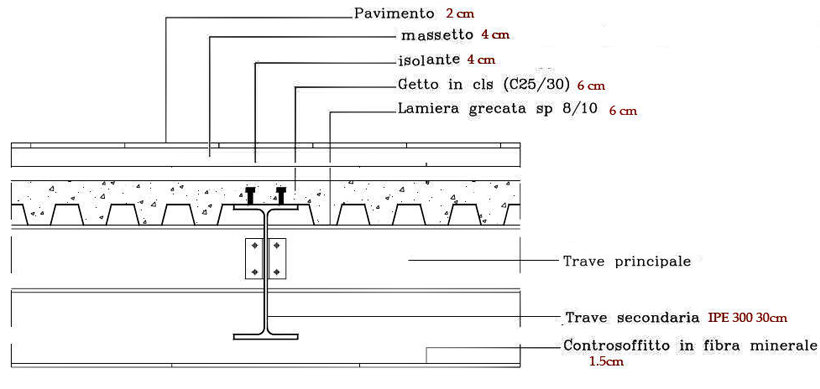
CARICO STRUTTURALE                             q_s = 1.869 kN/m²

CARICO PERMANENTE                               q_p = 2.502 kN/m²

CARICO ACCIDENTALE                               qa = 2 kN/m²

A questo punto inserisco i valori nella tabella Excel relativa al dimensionamento di una trave e ottengo il valore di q_u =  q_trave[kN/m] e M_max.

Scelgo un acciaio medio - classe Fe430 / s275 - con resistenza caratteristica di snervamento f_y,k = 275 MPa

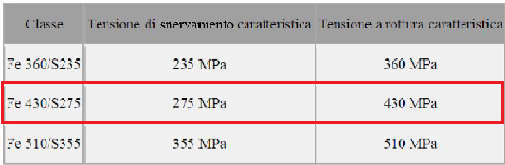
Inserendo il valore di f_y,k nel file Excel, il programma mi fornisce automaticamente il valore di  f_yd( tensione di progetto)  dividendo fyk  il coefficiente parziale di sicurezza per la resistenza delle membrature e la stabilità,  γs = 1,05 :

                                                                       f_yd = f_y,k / Y_s= 261.90 N/mm²

e  W_x,min (modulo di resistenza della sezione minimo)  attraverso la formula  

                                                                     W_x,min = M_max/ f_y,d = 547.83 cm³

ricavata direttamente dalla formula di Navier per la flessione [σ_max=(M_max/I_x) y_max = M_max/W ].

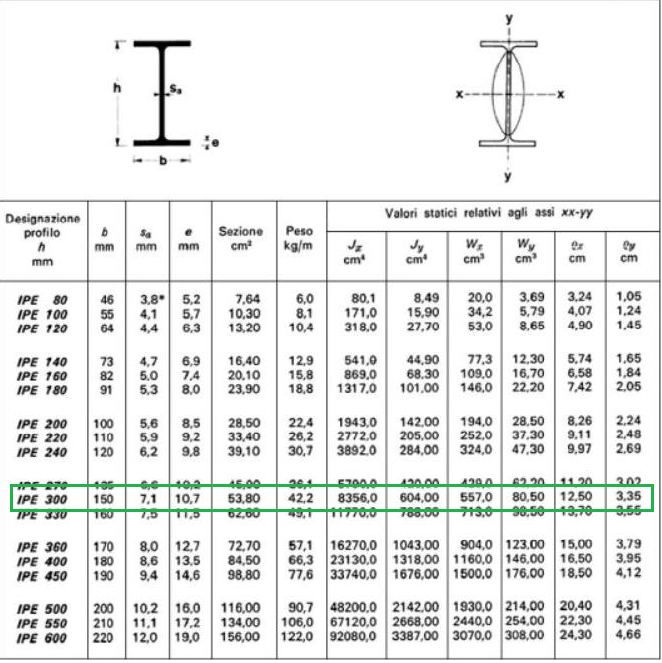
Fatto questo, posso scegliere il profilato IPE a partire dalla conoscenza del suo modulo di resistenza minimo W_min,ossia il minimo valore che la sezione deve avere affinchè il materiali non superi la tensione massima di progetto.

Ingegnerizzo il risultato e scelgo una trave IPE300 con Wx = 557 cm³.

 

TRAVE IN CEMENTO ARMATO

Prendo in esame la seguente sezione di solaio in latero-cemento e ne analizzo i carichi agenti su di un metro quadro:

SEZIONE SOLAIO IN CEMENTO ARMATO

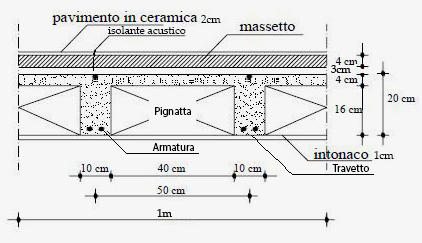
CARICO STRUTTURALE                             q_s =  2.25 kN/m²

CARICO PERMANENTE                               q_p = 2.829 kN/m²

CARICO ACCIDENTALE                               qa = 2 kN/m²

A questo punto inserisco i valori nella tabella Excel relativa al dimensionamento di una trave e ottengo il valore di q_u =  q_trave[kN/m] e M_max.

 

Per dimensionare la trave in cemento armato, la prima cosa da fare è scegliere la resistenza caratteristica rispettivamente dell'acciaio (f_yk) e del calcestruzzo (f_ck):

Utilizzo un acciaio B450 A  (f_yk= 450MPa) ed un calcestruzzo ordinario C 32/40  (f_ck = 32 MPa ) 

  ACCIAIO

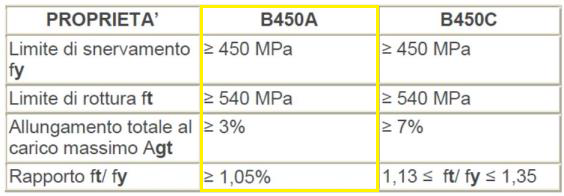
CALCESTRUZZO

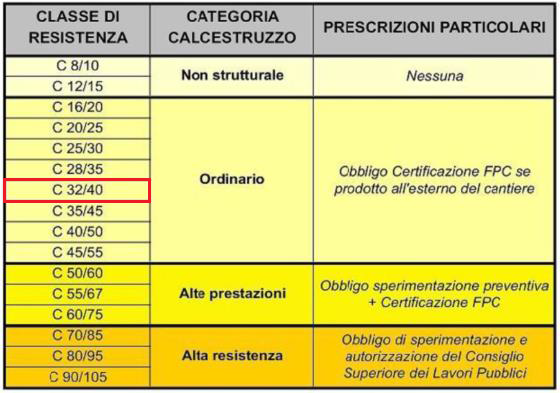
Tramite le resistenze caratteristiche, il foglio Excel mi calcola la tensione di progetto del calcestruzzo compresso (fc_d) e quella dell'acciaio (f_yd) tramite la formula:

                                                                          f_yd = f_yk / y_s

- con y_s coefficiente parziale di sicurezza relativo all'acciaio  di valore pari a 1,15 per gli acciai da armatura - e la formula:

                                                                       f_cd =  (f_ck / y_c) a_cc

con a_cc coefficiente riduttivo per le resistenze di lunga durata pari a 0,85, e y_c coefficiente parziale di sicurezza relativo al calcestruzzo pari a 1,5.

Posta b = 30 cm , e tramite i valori delle tensioni di progetto cosi ottenuti, si può determinare h_u (altezza utile della sezione) e da essa H_min(altezza minima della sezione)  che tiene conto anche di d, ossia la distanza tra il baricentro dell'armatura ed il filo del calcestruzzo teso, tramite la seguente formula:

                                                                        H_min = h_u + d

con h_u = r (M_max / b )^½                                         r = ( 2 / [f_cd(1-β/3)* β] )^½                              β= f_cd/ (f_cd+f_yd/n)      

L'altezza minima ottenuta (H_min) è uguale a 45,62 cm; ingegnerizzo la sezione e scelgo una trave in cemento armato con sezione 30 X 50 (H = 50 cm).

Il foglio Excel mi verifica in automatico la resistenza della trave scelta tenendo conto - insieme ai carichi - del suo peso proprio (moltiplicato per il fattore di sicurezza 1,3) a partire dalla conoscenza del peso specifico del cls armato pari a 25 kN/ m³.