Esercitazione 3_Verifica a Deformabilità di una Trave a Sbalzo (Mensola) in legno, acciaio e cemento armato

In questa esercitazione lo scopo è la verifica a deformabilità  della sezione di una trave a sbalzo nei tre materiali: legno, acciaio e cemento armato.

Per quanto riguarda il dimensionamento della trave, Il metodo di progetto  è analogo a quello utilizzato nella prima esercitazione, con una osservazione:

lo schema statico di riferimento qui considerato non è più una trave doppiamente appoggiata (esercitazione 2), bensì una mensola. Quindi il Momento massimo, in corrispondenza della sezione di incastro, varrà:

                                                             

                                                                     M_max = q_ul²/ 2

 

SCHEMA STATICO DI RIFERIMENTO: MENSOLA

 

 Prendo in esame un'ipotetica pianta di carpenteria con una maglia strutturale in cui le ultime due campate                sull'estremità destra sono aggettanti e ne individuo la trave maggiormente sollecitata , con la sua area di influenza.

 

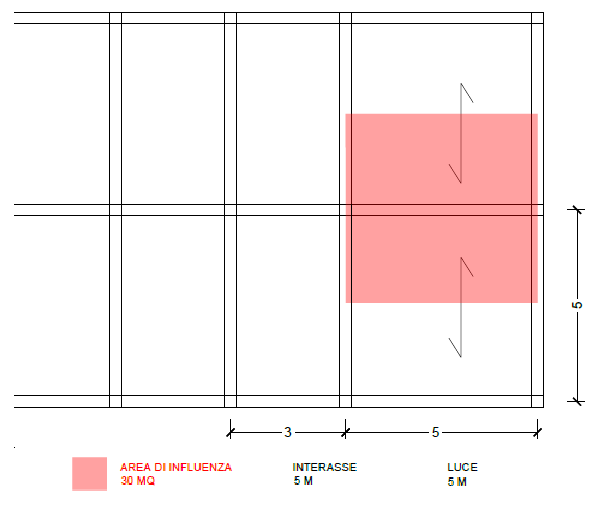
VERIFICA A DEFORMABILITA'

Dimensionata la sezione della trave, la verifica a deformabilità controllando l'abbassamento massimo della mensola in rapporto alla sua luce. Questo, è un procedimento che verrà effettuato allo Stato Limite di Esercizio (SLE) poichè, in questo caso,non è richiesta la verifica a rottura (SLU) ma solo controllare che non vi siano spostamenti e deformazioni che possano compromettere l'utilizzo e l'efficienza della costruzione, insieme al suo aspetto.

A questo fine, carichi incidenti sulla struttura sono ricombinati seguendo la combinazione frequente, impiegata solitamente per gli stati limite di esercizio reversibili:

                                                                 

                                                                q_e= (G₁ + G₂ + ψ11Q₁) x i

 

(G1 è il valore caratteristico del peso del carico strutturale q_s e G₂ del peso del carico permanente q_p, mentre  ψ₁₁ è un coefficiente che definisce il valore frequente di Q1che rappresenta il valore caratteristico dell’azione variabile q_a).

In questa fase, bisognerà anche controllare, a seconda della tecnologia utilizzata, se considerare o meno il peso proprio della trave poichè essa, se rilevante ai fini del risultato, verrà riutilizzata per calcolare il carico totale q_e (il file Excel relativo a questa esercitazione lo farà in automatico).

Infine, per calcolare lo spostamento, è necessario conoscere il modulo elastico della sezione (E) ed il suo momento di inerzia (I_X). Inserite queste informazioni nel file Excel, il programma ci fornirà in automatico il valore dell'abbassamento massimo (v_max) attraverso la formula:

                                                                       v_max = q_el⁴/ 8 E I_x

con  q_e (kN/m) = carico totale di esercizio

       l(m)         = luce trave 

       E             = modulo elastico del materiale 

       I_x (cm⁴)    = momento di inerzia della sezione 

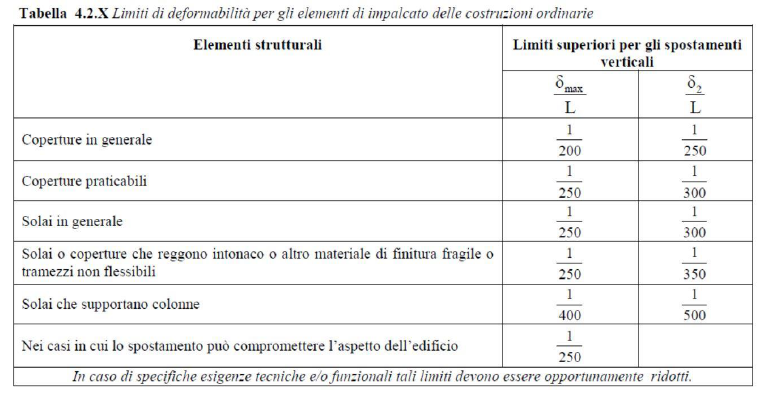
verificando che il rapporto tra la luce della trave e il suo spostamento massimo (v_max) sia maggiore di 250, come imposto dalla normativa in base al tipo di elemento strutturale considerato.

                                                                                    l / v_max ≥ 250

 

TRAVE IN LEGNO

 

Dimensionamento

Riprendendo il procedimento svolto nell'esercitazione 2 (dimensionamento di una trave in legno,acciaio e cemento armato), a partire da una sezione data, ottengo:

Sezione Trave

 

Carico totale agente sulla trave e  Momento massimo

Come abbiamo già detto, lo schema isostatico in questo caso è quello di una mensola, dunque il Momento massimo sarà il quadruplo di quello relativo allo schema isostatico di una trave appoggiata (M_max,mensola = ql²/2 ):

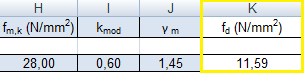
Tensione di Progetto

 

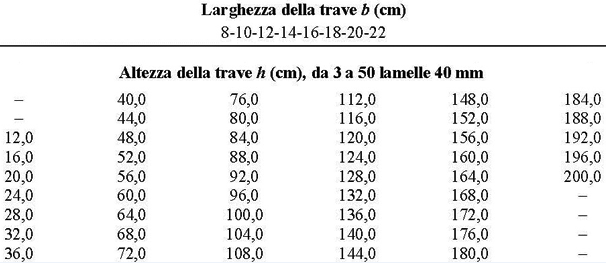
Scelta della trave, data la base 

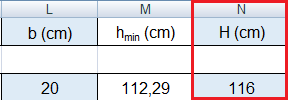
Ipotizzando di avere una base di 20 cm (b = 20 cm) otterrò un'altezza minima che, dopo essere stata ingegnerizzata, mi porterà a scegliere una trave di dimensioni 20 X 116 cm.

                                                     

      

 

Verifica a Deformabilità

 

Carico di esercizio (q_e) e incidenza del peso proprio della trave

Definita la sezione, il programma mi fornisce subito la combinazione di carico di esercizio q_e combinando i carichi di esercizio secondo la combinazione frequente chiarita sopra e, poichè il legno è un materiale leggero viene trascurato il peso proprio della trave.

q_e,legno = 21 kN/m

 

Spostamento trasversale massimo

Per calcolare lo spostamento, inserisco nel file Excel il valore del modulo elastico del legno ( E ) - per la verifica allo SLE và preso in considerazione il modulo elastico medio parallelo E_0,g,mean , da sostituire invece con quello caratteristico E_0,g,05 per la verifica allo SLU - che per il legno lamellare da me scelto è E = 126 000 N/mm²

 

ed il foglio di calcolo mi fornisce il valore del momento di inerzia della sezione (I_x). Nel caso presente, che presenta l'analisi di una sezione di legno rettangolare, I_x = bh³/ 12.

A questo punto, il programma ha tutti i dati necessari per calcolarmi anche l'abbassamento massimo della mensola secondo la formula scritta sopra (v_max = q_el⁴/ 8 E Ix ):

v_{max, legno} = 0.05 cm 

 

Verifica

La sezione è verificata, come mi conferma la tabella di calcolo, dal fatto che il rapporto fra la luce della trave e il suo spostamento massimo è di gran lunga maggiore di 250 (verifica ⇔ l/v_max  ≥ 250) :

l / v_{max, legno} = 9872,21 >250 

 

TRAVE IN ACCIAIO

Come per il caso della trave in legno, riprendendo il procedimento svolto nell'esercitazione 2 (dimensionamento di una trave in legno,acciaio e cemento armato), a partire da una sezione data ottengo:

Sezione Trave

 

Carico totale agente sulla trave e  Momento massimo

Come abbiamo già detto, lo schema isostatico in questo caso è quello di una mensola, dunque il Momento massimo sarà il quadruplo di quello relativo allo schema isostatico di una trave appoggiata (M_max,mensola = ql²/2 )

 

Tensione di Progetto e Modulo di Resistenza minimo

Scelto un acciaio medio - classe Fe360 / s235 - con resistenza caratteristica di snervamento f_y,k =235MPa, ottengo f_y,d e W_x,min. 

 

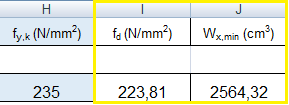
Scelta della Trave

 I valori trovati mi portano a scegliere un profilato IPE 600 che avrà un modulo di resistenza  W_x = 3070.0 cm³  ed un momento di inerzia I_x= 92080 cm^4.

 

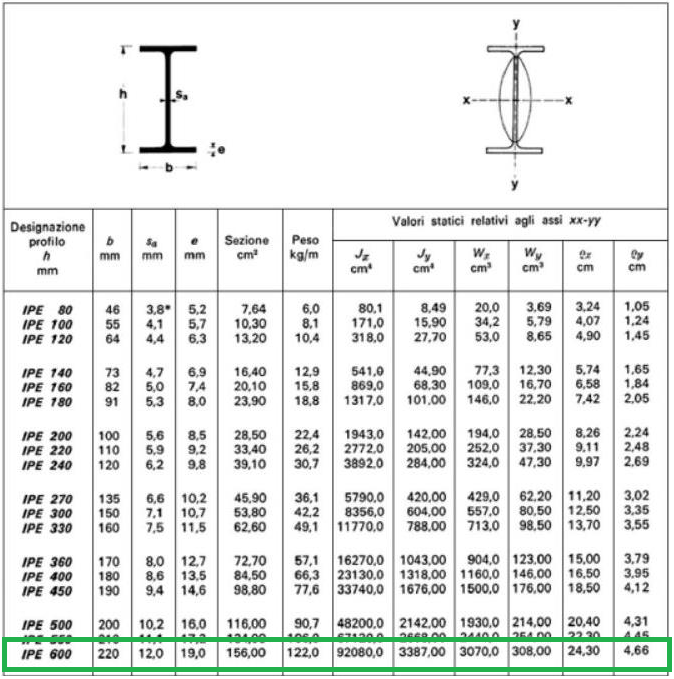
Verifica a Deformabilità

 

Carico di esercizio (q_e) e incidenza del peso proprio della trave

Definita la sezione, inseriamo nel foglio di calcolo il momento di Inerzia del profilato e il suo peso proprio, il cui contributo, nel caso dell'acciaio, ha un contributo significativo ai fini dell'analisi progettuale.

I_x= 92080 cm⁴                                                      Peso = 122 kg/m = 1.22 kN/m

 

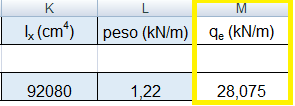
Spostamento trasversale massimo

Per calcolare lo spostamento infine, inserisco nel file Excel il anche il valore del   modulo elastico dell'acciaio 

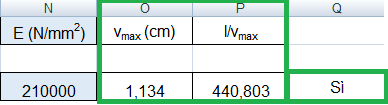
 E = 210000 N/mm²  ed ottengo l'abbassamento massimo della mensola in acciaio (v_max = q_el⁴/ 8 E Ix ):

v_{max, acciaio} =  1.134 cm

 

Verifica

Anche in questo caso, la sezione è verificata, come mi conferma la tabella di calcolo.Il rapporto fra la luce della trave e il suo spostamento massimo infatti, è maggiore di 250 (verifica ⇔ l/v_max  ≥ 250) :

l / v_{max, acciaio} = 440.803  >250 

 

 

TRAVE IN CEMENTO ARMATO

Anche qui, riprendendo il procedimento svolto nell'esercitazione 2 (dimensionamento di una trave in legno,acciaio e cemento armato), a partire da una sezione data ottengo:

Sezione Trave

 

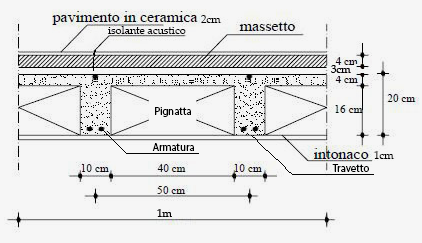
Carico totale agente sulla trave e  Momento massimo

Di nuovo,lo schema isostatico in questo caso è quello di una mensola, dunque il Momento massimo sarà il quadruplo di quello relativo allo schema isostatico di una trave appoggiata (M_max,mensola = ql²/2 )

 

Tensioni di Progetto

Utilizzo un acciaio B450 A  (f_yk= 450MPa) ed un calcestruzzo ordinario C 32/40  (f_ck = 40 MPa ). Tramite le resistenze caratteristiche, il foglio Excel mi calcola la tensione di progetto del calcestruzzo compresso (fc_d) e quella dell'acciaio (f_yd)

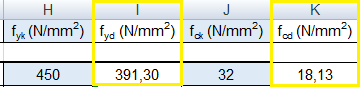
Scelta della Trave

Posta b = 40 cm , e tramite i valori delle tensioni di progetto cosi ottenuti, si può determinare h_u (altezza utile della sezione) e da essa H_min(altezza minima della sezione) come analizzato nell'esercitazione 2. 

L'altezza minima ottenuta (H_min) è uguale a 75,36 cm; ingegnerizzo la sezione e scelgo una trave in cemento armato con sezione 30 X 90 (H = 90 cm).  

Il foglio Excel mi verifica in automatico la resistenza della trave scelta tenendo conto - insieme ai carichi - del suo peso proprio (moltiplicato per il fattore di sicurezza 1,3) a partire dalla conoscenza del peso specifico del cls armato pari a 25 kN/ m³.

 

 

Verifica a Deformabilità

 

Carico di esercizio (q_e) e incidenza del peso proprio della trave

Anche nel caso del cemento armato, bisognerà tenere conto del peso proprio della trave (ricavato automaticamente da Excel) ; il foglio di calcolo, tenendone conto,mi fornisce il valore del carico di esercizio tramite la combinazione frequente dei carichi incidenti.

q_{e,cls armato} = 39,40 kN/m

 

Spostamento trasversale massimo

Per calcolare lo spostamento infine, inserisco nel file Excel il anche il valore del   modulo elastico del calcestruzzo

C 32740 pari a  E = 33300 N/mm²  ed ottengo l'abbassamento massimo della mensola in acciaio (v_max = q_el⁴/ 8 E Ix ):

v_{max, cls armato} =  0.38 cm

 

Verifica

Anche in questo caso, la sezione è verificata, come mi conferma la tabella di calcolo.Il rapporto fra la luce della trave e il suo spostamento massimo infatti, è maggiore di 250 (verifica ⇔ l/v_max  ≥ 250) :

l / v_{max, acciaio} = 1314,59  >250