III ESERCITAZIONE: verifica deformabilità di una mensola ( tecnologie: legno, acciaio, calcestruzzo armato)
Per la terza esercitazione dovevamo verificare la deformabilità di una mensola con l'ausilio di un foglio di calcolo excell, composto di tre fogli, uno per ognuna delle tre tecnologie da analizzare.
Il metodo di calcolo qui utilizzato simile nella prima parte a quello utilizzato nella seconda esercitazione, ossia poniamo la tensione massima della trave pari a quella di progetto del materiale.
Partiremo quindi da un telaio di nostra scelta
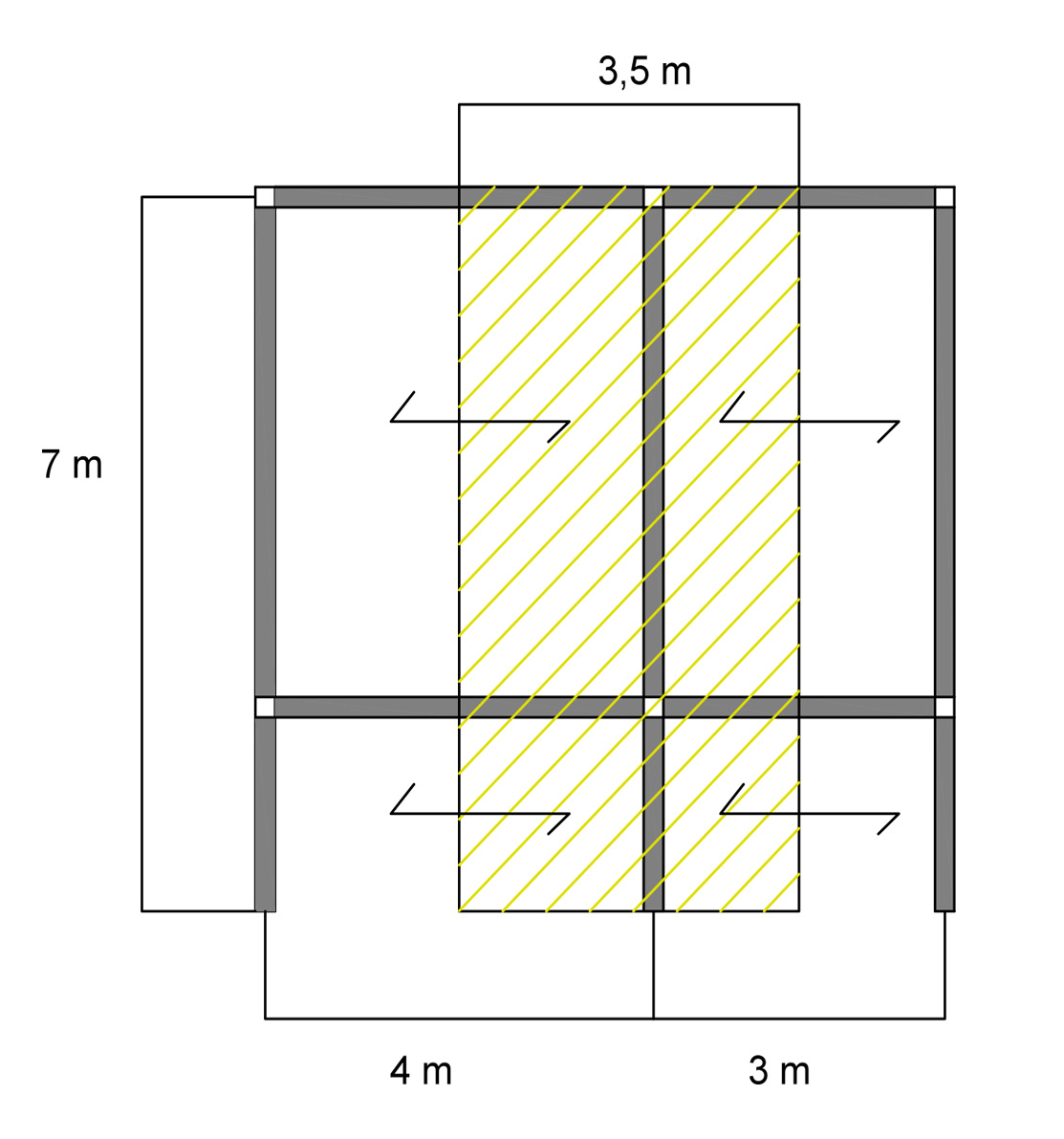
La mensola da noi analizzata avrà un interasse pari a 3,5 m e una luce pari a 2 m.
Andremo quindi a inserire tali valori nei tre fogli di calcolo excell.
LEGNO
Per poter completare le colonne che seguono analizzeremo le diverse tecnologie di solaio, partendo dal legno.
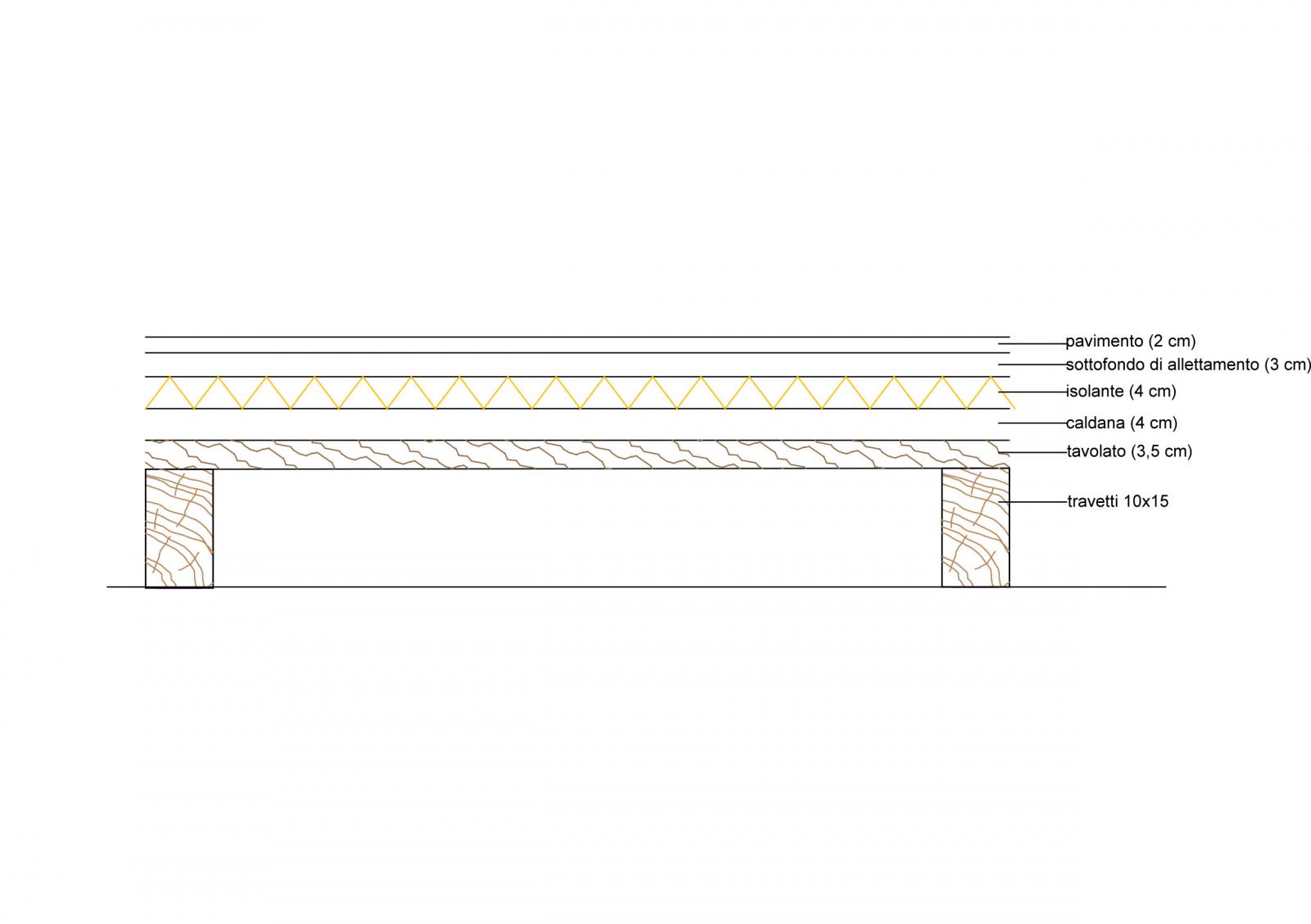 Passiamo quindi a definire quali sono gli elementi portanti di un solaio in legno e quali glie elemnti portati.
Passiamo quindi a definire quali sono gli elementi portanti di un solaio in legno e quali glie elemnti portati.
Per questa prima tecnologia glie elementi portanti saranno composti da travetti in legno 10 cm x 15 cm e dal tavolato.Quindi:
qs: travetti = 6 KN/mc x 2( 0,1 m x 0,15 m)= 18 KN/mq
tavolato= 6 KN/mc x 0,035 m = 0,21 KN/mq
qs= 0,39 KN/mq
Invece per quanto riguardi gli elementi portati questi sono composti da massetto, sottofondo di allettamento, pavimento. Quindi:
qp: massetto= 20 KN/mc x 0,04 m= 0,80 KN/mq
allettamento= 20 KN/mc x 0,03 m = 0,6 KN/mq
pavimento= 4 KN/mq
incidenza impianti= 0,1 KN/mq
incidenza tramezzi= 1,6 KN/mq
qp= 3,5 KN/mq
Per quanto riguarda invece il carico accidentale esso è stabilito dalla normativa e dipende dall'uso a cui è adibito l'edificio che stiamo analizzando. Nel nostro caso essendo l'edificio adibito ad uso di civile abitazione
qa= 2 KN/mq
Inseriamo quindi i valori ottenuti all'interno del foglio di calcolo excell relativo al legno

Calcoleremo quindi il carico ultimo gravante sulla trave attraverso la formula
qu= (1,3qs + 1,5qp + 1,5qa) x i
Inserendo poi la luce possiamo calcolare ora il momento massimo M max della mensola
M max= ql^2/2
Ossia la formula parametrica per il calcolo del momento max di una mensola
M(s)= ql x s - qs^2/2
M(l)= ql^2 - ql^2/2= ql^2/2
Andiamo quindi ora a definire la tipologia di legno da utilizzare per la nostra sezione
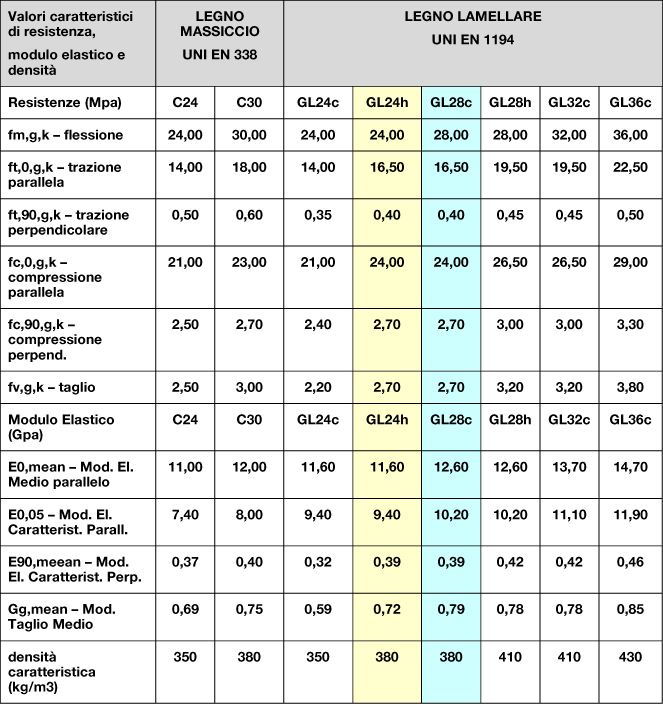
Utilizzando un legno massiccio C24 la nostra tensione caratteristica sarà pari a fk= 24 N/mm^2
Possiamo quindi ricavare la tensione di progetto
fd= kmod x fk/ ym
dove kmod è pari a 0,8 e ym pari a 1,5
Fissando ora una base per la nostra sezione, calcoleremo l'altezza min
H min=√ 6 Mmax/ b x fd
Ingegnerizziamo quindi il valore scegliendo un'altezza compatibile con i profilati sul mercato subito maggiore a quella trovata.
Una volta dimensionata la nostra sezione dobbiamo calcolare l'abbassamento della nostra mensola: essendo una verifica ad una deformazione e non al collasso, questa srà una verifica agli SLE (Stati Limite di Esercizio)
Ricalcoreremo quindi il carico gravante sulla mensola agli SLE per la combinazione ad uso frequente
qe= (qs + qp + ψ1j) x i
Possiamo ora calcolare il modulo di inerzia
Ix= (b x h^3)/ 12
Avendo anche definito il modulo elastico E del materiale possiamo infine calcolare l'abbassamento massimo della mensola
v max= ql^4/ 8EI
Secondo la normativa deve essere verificato che il rapporto tra la luce della trave e l'abbassamento max sia maggiore di 250
l = 2 m e vmax= 0,23 cm
l / v max= 200 / 0,23= 869,56 cm > 250
ACCIAIO
Calcoleremo ora l'abbassamento max di una trave per la tecnologia dell'acciaio
 Per quanto riguarda un solaio in acciaio dobbiamo prima di tutto calcolare nuovamente il carico strutturale, permanente e accidentale, usando lo stesso procedimento adottato per il legno
Per quanto riguarda un solaio in acciaio dobbiamo prima di tutto calcolare nuovamente il carico strutturale, permanente e accidentale, usando lo stesso procedimento adottato per il legno
Il carico strutturale sarà comopsto da lamiera grecata e getto in cls armato per un totale di
qs= 1,8 KN/mq
I carichi portati saranno invece composti da massetto, pavimento ed isolante per un totale di
qp= 2,7 KN/mq
il carico accidentale rimarrà qa= 2 KN/mq da normativa
Inseriamo quindi i nuovi valori nel foglio di calcolo excell dell'acciaio

Ottengo quindi il carico ultimo qu attraverso la formula
qu= 1,3qs + 1,5qp + 1,5qa
Avendo il carico ultimo e la luce della trave possiamo calcolare il momento max della mensola
M max= ql^2/2
Sciegliamo il tipo di acciaio da utilizzare per la nostra sezione e ne inseriamo la tensione caratteristica, nel nostro caso fk=235 N/mm^2
Siamo quindi in grado di ricavare la tensione di progetto
fd= fk/ ys
dove ys è pari per l'acciaio a 1,05
Ora calcoleremo il modulo di resistenza a flessione min
Wmin= M max/ fd
Ottenuto il valore di Wmin possiamo dimensionare la trave attraverso un profilario scegliendo la sezione corrisponde al modulo di resistenza a flessione subito maggiore a quello ottenuto
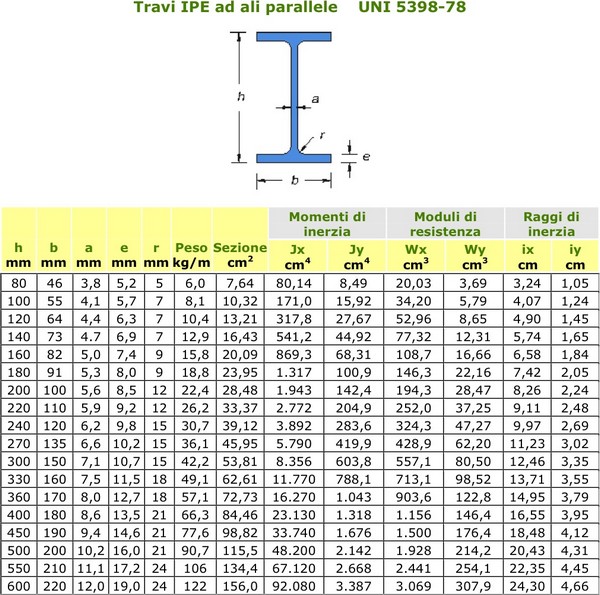
Inseriamo ora i valori Ix e il peso corrispondente alla nostra sezione nel foglio di calcolo
Ricalcoliamo il carico allo SLE per combinazione frequente
qe=( qs + qp +ψ1j) x i + peso trave
Inserendo ora il modulo elastico E dell'acciaio possiamo calcolare l'abbassamento
v max= ql^4/ 8EI
Dobbiamo quindi per concludere verificare che il rapporto tra la luce della nostra trave e l'abbassamento max sia maggiore del valore definito dalla normativa
l / v max > 250
CLS ARMATO
Analizziamo infine la tecnologia del cls armato, ricalcolando nuovamente carico strutturale, portante e accidentale riguardanti un solaio in cls armato
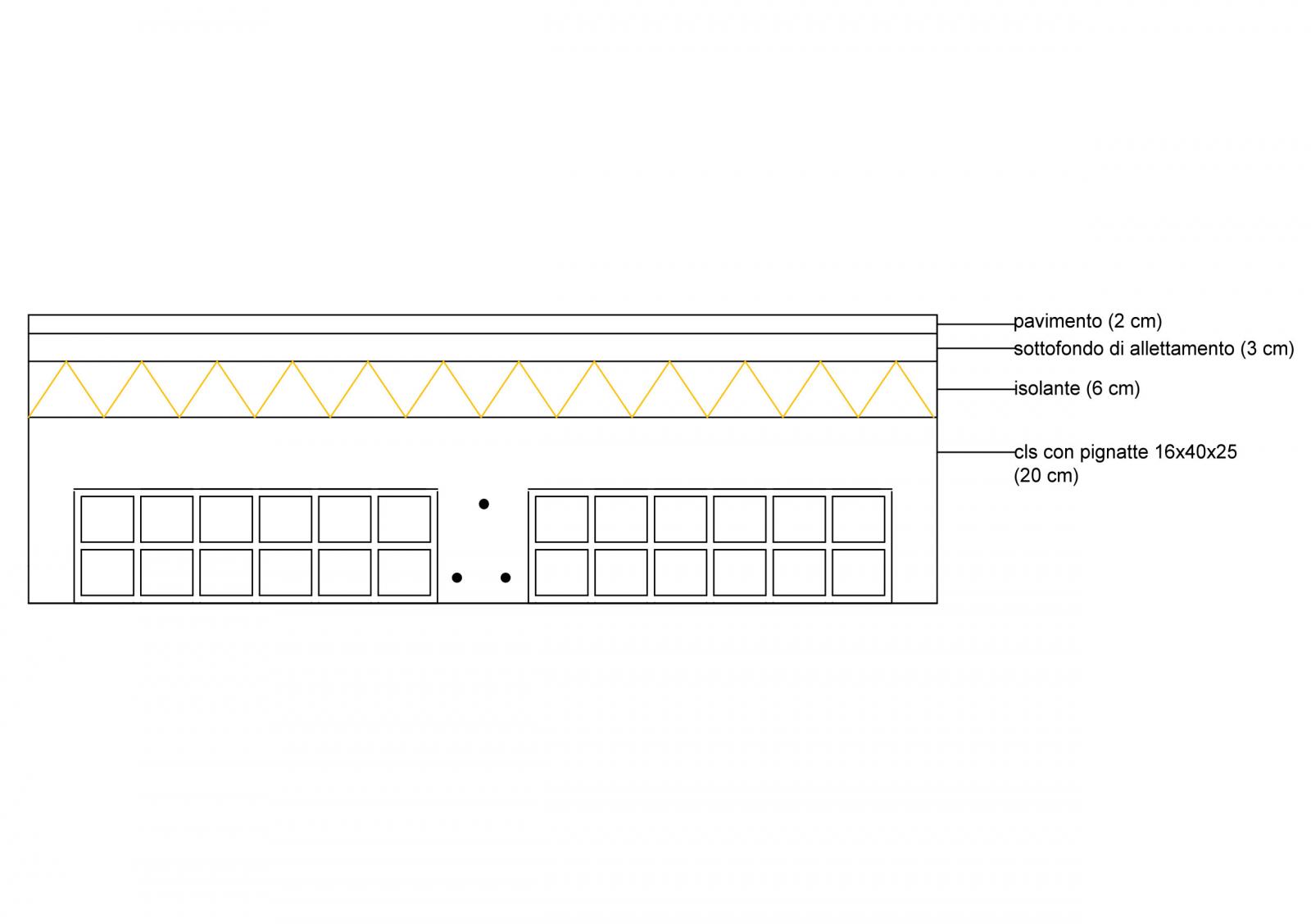 In questo caso il carico strutturale sarà composto da pignatte, soletta in cls per un totale di
In questo caso il carico strutturale sarà composto da pignatte, soletta in cls per un totale di
qs= 0,61 KN/mq
Gli elementi portati saranno invece il sottofondo di allettamento, l'isolante e il pavimento, per un totale di
qp= 2,7 KN/mq
il carico accidentale rimane qa= 2 KN/mq da normativa
Inseriamo quindi i nuovi valori all'interno del foglio di calcolo excell
 Calcoleremo quindi il carico ultimo attraverso la formula
Calcoleremo quindi il carico ultimo attraverso la formula
qu= 1,3qs + 1,5qp + 1,5qa
Ora avendo il carico ultimo e la luce della trave possiamo calcolare il momento massimo della mensola
M max= ql^2/2
Fissiamo in seguito l'acciaio che comporrà le bare della nostra sezione e ne riportiamo la tensione caratteristica( nel nostro caso fk= 450 N/ mm^2 e otteniamo da questa la tensione di progetto
fd= fyk/ ys
Allo stesso modo riportiamo la tensione caratteristica del calcestruzzo della nostra sezione
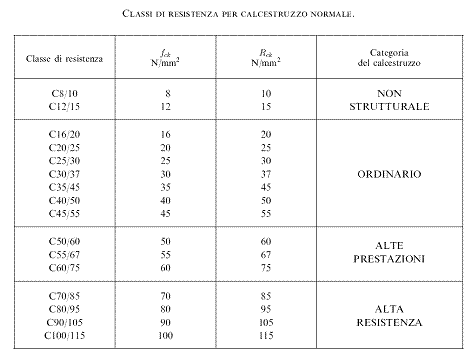
Nel nostro caso è stato scelto un calcestruzzo C30/37 con fck= 30 N/ mm^2
Otteniamo quindi la tensione di progetto fd= 0,85 x fck/ 1,5
Calcoliamo ora β= fcd/ (fcd + fd/n) dove n=15
Fissando una base otterremo l'altezza utile della nostra sezione hu, a cui dovrà essere sommata la lunghezza del copriferro. Il valore di H ottenuto dovrà poi essere ingegnerizzato.
Calcoliamo quindi ora l'area della sezione( A= b x H essendo una sezione rettangolare), il peso della nostra sezione, moltiplicando il peso specifico del materiale del l'area della sezione.
Avendo ora il peso della sezione possiamo calcolare il carico alla combinazione frequente
qe=(qs + qp + ψ1j) x i + peso
Riporto il modulo elastico E del materiale e calcolo il modulo di inerzia
I= b x h^3/12
Ora disponiamo quindi di tutti gli elementi necessari per calcolare l'abbassamento max della mensola
v max= ql^4/ 8EI
Dobbiamo infine verificare che questo soddisfi la condizione per cui il rapporto tra luce della trave e abbassamento max debba essere maggiore di 250
l / v max > 250
