Esercitazione 3 : dimensionamento di una mensola

Dopo aver disegnato un solaio a scelta selezionare la trave più sollecitata, definire il dimensionamento di essa con diverse tipologie di solaio ed eseguire le verifiche degli abbassamenti massimi.

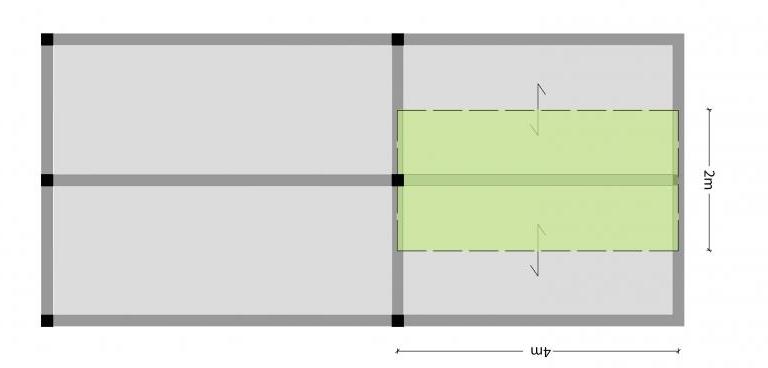
1. DIMENSIONAMENTO DELLE MENSOLE

Come nella precedente esercitazione, per dimensionare la trave, calcolare i carichi che agiscono su di essa          (Qu= (Qs x γ_G1 + Qp x γ_G2  + Qa x γ_G3  x interasse) e calcolare il momento massimo. La trave in questo caso non è più appoggiata ma si comporta come una mensola. Quindi il momento massimo non sarà più M_max= Q_u x l²/8 ma si prenderà in considerazione per i calcoli l’espressione:

        → M_max=Q_u x l²/2

• DIMENSIONAMENTO TRAVE IN LEGNO

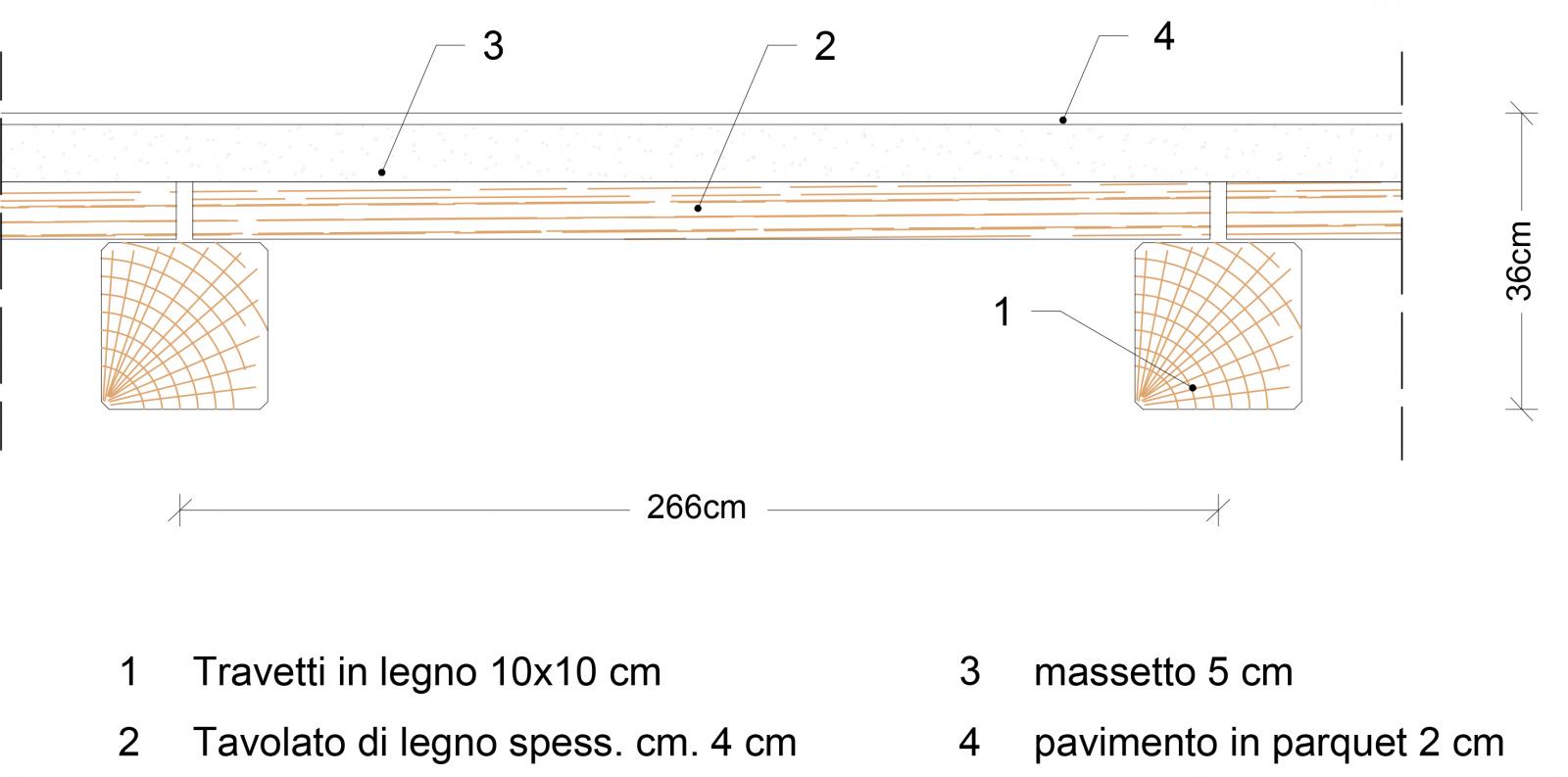
Scelta la tipologia di solaio e studiata la stratigrafia con un analisi dei carichi si ottiene un M_max

In seguito scegliendo una tipologia di legno (lamellare GL28h), tenendo conto di alcuni coefficienti di sicurezza e impostando una base predefinita trovare l’altezza minima della trave.Cercare su un formulario l’altezza di progetto prendendo un altezza che superi l’altezza minima.In questo caso si otterrà una trave 25x50.

• DIMENSIONAMENTO TRAVE CLS ARMATO

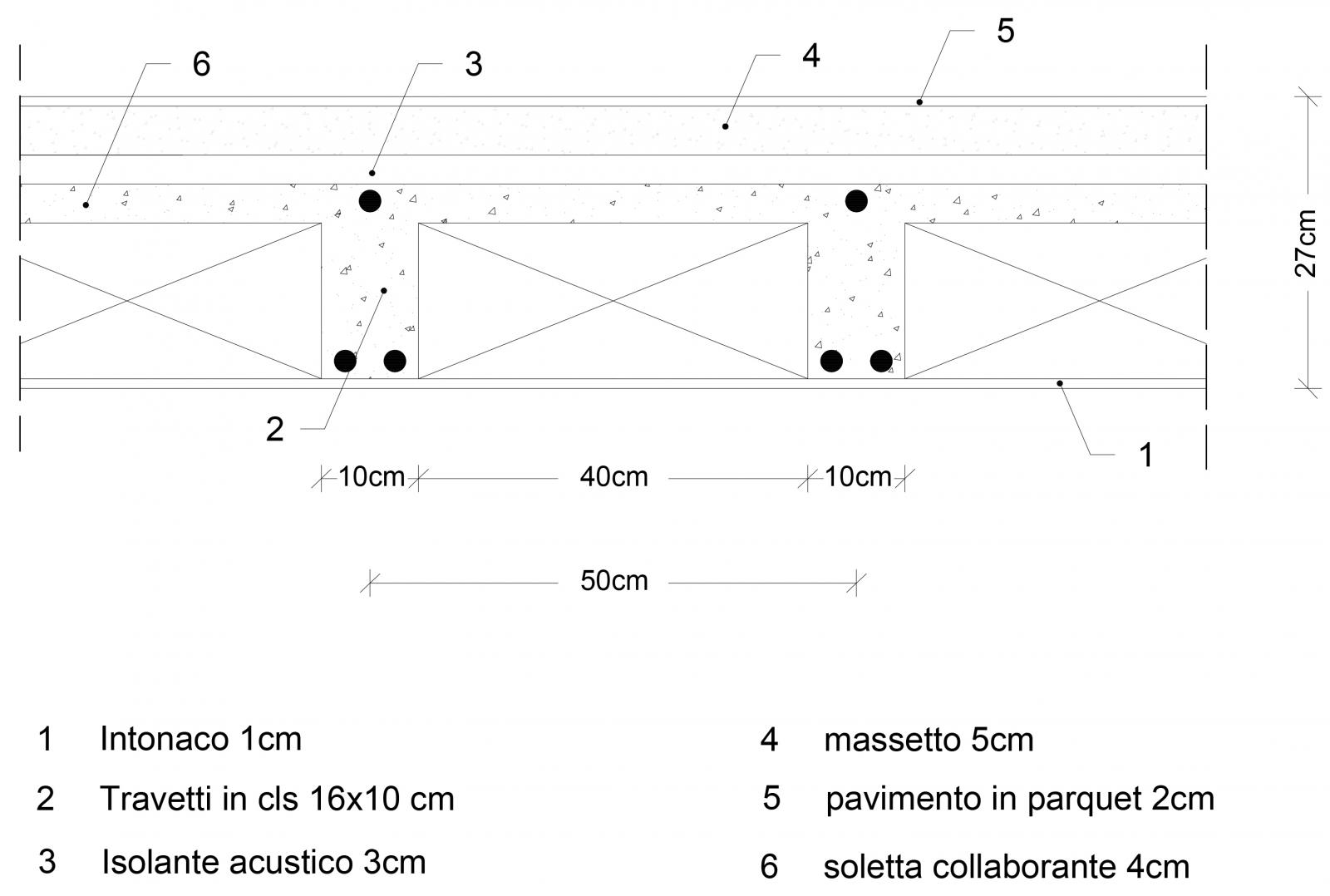
Scelta la tipologia di solaio e studiata la stratigrafia con un analisi dei carichi si ottiene un M_max

Essendo un materiale non omogeneo (acciaio S450 e calcestruzzo C50) calcolare le due tensioni di progetto: dell’acciaio f_yk e del calcestruzzo f_ck. In seguito definire una base e trovare un’altezza, sempre considerando un ‘altezza maggiore dell’H_min trovata. Infine verificare che il peso proprio della trave non influisca il dimensionamento iniziale con il carico Q_u. In questo caso si ottiene una trave 30x40.

• DIMENSIONAMENTO TRAVE IN ACCIAIO

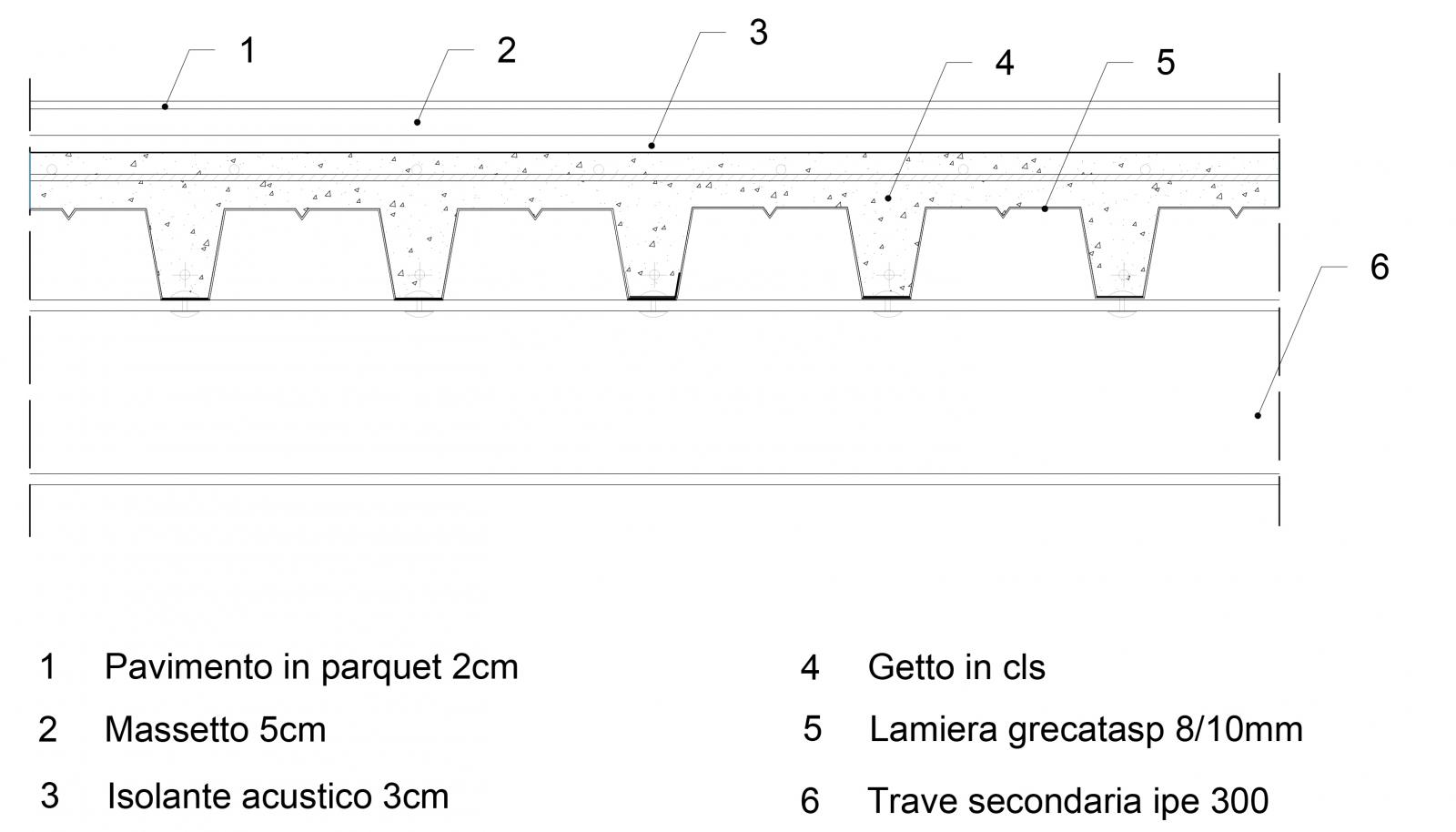
Scelta la tipologia di solaio e studiata la stratigrafia con un analisi dei carichi si ottiene un M_max

In seguito scegliendo una tipologia di acciaio (acciaio S235), grazie alla tensione di progetto f_yk, trovare il modulo di resistenza a flessione minimo. Infine trovare una tipologia di IPE che abbia un Wd>Wxmin (in questo caso IPE360).

2. CALCOLO E VERIFICA ABBASSAMENTI MENSOLA

Calcolare l’abbassamento massimo di ogni mensola con la formula

        → V_max = (q_e x l⁴)/(8EI_x)

Considerando che non deve superare 1/250 della luce (che in questo caso è 4m)

        → (l/V_max)>250

• CALCOLO E VERIFICA TRAVE IN LEGNO

Applicare la combinazione di carico agli SLE per la combinazione ad uso frequente qe ed inserire il modulo di elasticità E del legno per ottenere il momento d’inerzia I_x.

       → qe= (qs + qp + ψ1j) x i = 8KN/m

       → Ix= (b x h^3)/ 12 = 260417cm⁴

Quindi calcolare l'abbassamento massimo con la formula:

       → V_max = (q_e x l⁴)/(8EI_x)= 1,20cm

e verificare come da normativa che (l/V_max)>250 →  (l/V_max)= 334>250 a questo punto l'asta è dimensionata e verificata.

• CALCOLO E VERIFICA TRAVE IN CALCESTRUZZO ARMATO

Conoscendo base e altezza calcolare l'area della sezione ( A= b x H ) e il peso di essa, moltiplicando il peso specifico del materiale per l'area della sezione.Nel calcestruzzo deve essere considerato nel calcolo anche il peso proprio della trave poichè è un materiale molto pesante e potrebbe influire con i calcoli del dimensionamento e della verifica.

Applicare la combinazione di carico agli SLE per la combinazione ad uso frequente qe ed inserire il modulo di elasticità E per ottenerei il momento d’inerzia I_x.

       → qe=(qs + qp + ψ1j) x i + peso = 15.44Kn/m

       → Ix= (b x h^3)/ 12 = 160000cm⁴

Quindi calcolare l'abbassamento massimo con la formula:

       → V_max = (q_e x l⁴)/(8EI_x)= 1,47cm

e verificare come da normativa che (l/V_max)>250 →  (l/V_max)=272>250 a questo punto l'asta è dimensionata e verificata.

• CALCOLO E VERIFICA TRAVE IN ACCIAIO

Applicare la combinazione di carico agli SLE per la combinazione ad uso frequente qe (considerando il peso della trave) ed inserire il modulo di elasticità E e il momento d’inerzia Ix. Nel caso della trave in acciaio non è necessario calcolare il momento d'inerzia poichè è tabellato: trovato Wx si sceglie una IPE e si trova un momento d'inerzia predefinito.

       → qe=(qs + qp + ψ1j) x i + peso =12.451Kn/m

Quindi calcolare l'abbassamento massimo con la formula:

       → V_max = (q_e x l⁴)/(8EI_x)= 1.166cm

e verificare come da normativa che (l/V_max)>250 →  (l/V_max)=343>250 a questo punto l'asta è dimensionata e verificata.